【ゼロからのTellusの使い方】Jupyter Labで富士山の標高グラフを作成する
ASTER GDEMとは、NASAの地球観測衛星Terraに搭載されたASTERという光学センサの観測データを元に作成された数値標高モデルです。本記事ではASTER GDEM 2.0の標高データを使って、TellsuのJupyter Labで富士山の標高グラフを作成する方法を紹介します。
記事作成時から、Tellusからデータを検索・取得するAPIが変更になっております。該当箇所のコードについては、以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/access/traveler_api_20220310_
firstpart.html
2022年8月31日以降、Tellus OSでのデータの閲覧方法など使い方が一部変更になっております。新しいTellus OSの基本操作は以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/tellus_os/start_tellus_os.html
本記事ではJupyter Labで富士山の標高グラフを作成する方法を紹介します。
TellusでJupyter Lab(Jupyter Notebook)を使う方法は、「Tellusの開発環境でAPI引っ張ってみた」をご覧ください。
1.標高データ(ASTER GDEM 2.0)を取得する
TellusではASTER GDEM 2.0という標高データを利用することができます。
ASTER GDEMとは、NASAの地球観測衛星Terraに搭載されたASTERという光学センサの観測データを元に作成された数値標高モデルです。
ASTER GDEM 2.0はそのバージョン2にあたり、緯度経度が1秒角(およそ30メートル)、高さ方向が1メートルの分解能で地球全域の標高を得ることができます。
※標高は建物や木の高さを含んだ数値です。一部、建物や木の高さを含まない箇所もあります。
データはAPIにより標高タイルという形式で取得することができます。標高タイルとは、地図タイルと同一の座標を用いて、PNG画像として標高データを表現するフォーマットです。各ピクセルの緯度経度は左上を値を代表値とし、RGB値から標高を算出することができます。
参考:標高タイルの詳細仕様
APIの使い方はこちらのAPIリファレンスにまとめられています。
※データを利用する際は、データ詳細のデータポリシーを確認して、規約を違反しないように注意してください。
https://gisapi.tellusxdp.com/astergdem2/dsm/{z}/{x}/{y}.png引数
| z | 必須 | Zoom Level 0-12 |
| x | 必須 | タイルのX座標 |
| y | 必須 | タイルのY座標 |
このAPIをJupyter LabのNotebookから呼び出してみましょう。
Tellus IDEを開き、「work」ディレクトリに移動してから「Python3」を選択し、以下のコードを貼り付けます。
import requests, json
from skimage import io
from io import BytesIO
%matplotlib inline
TOKEN = 'ここには自分のアカウントのトークンを貼り付ける'
def get_astergdem2_dsm(zoom, xtile, ytile):
"""
ASTER GDEM2 の標高タイルを取得
Parameters
----------
zoom : str
ズーム率
xtile : str
座標X
ytile : number
座標Y
Returns
-------
img_array : ndarray
標高タイル(PNG)
"""
url = " https://gisapi.tellusxdp.com/astergdem2/dsm/{}/{}/{}.png".format(zoom, xtile, ytile)
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url, headers=headers)
return io.imread(BytesIO(r.content))
img_12_3626_1617 = get_astergdem2_dsm(12, 3626, 1617)
io.imshow(img_12_3626_1617)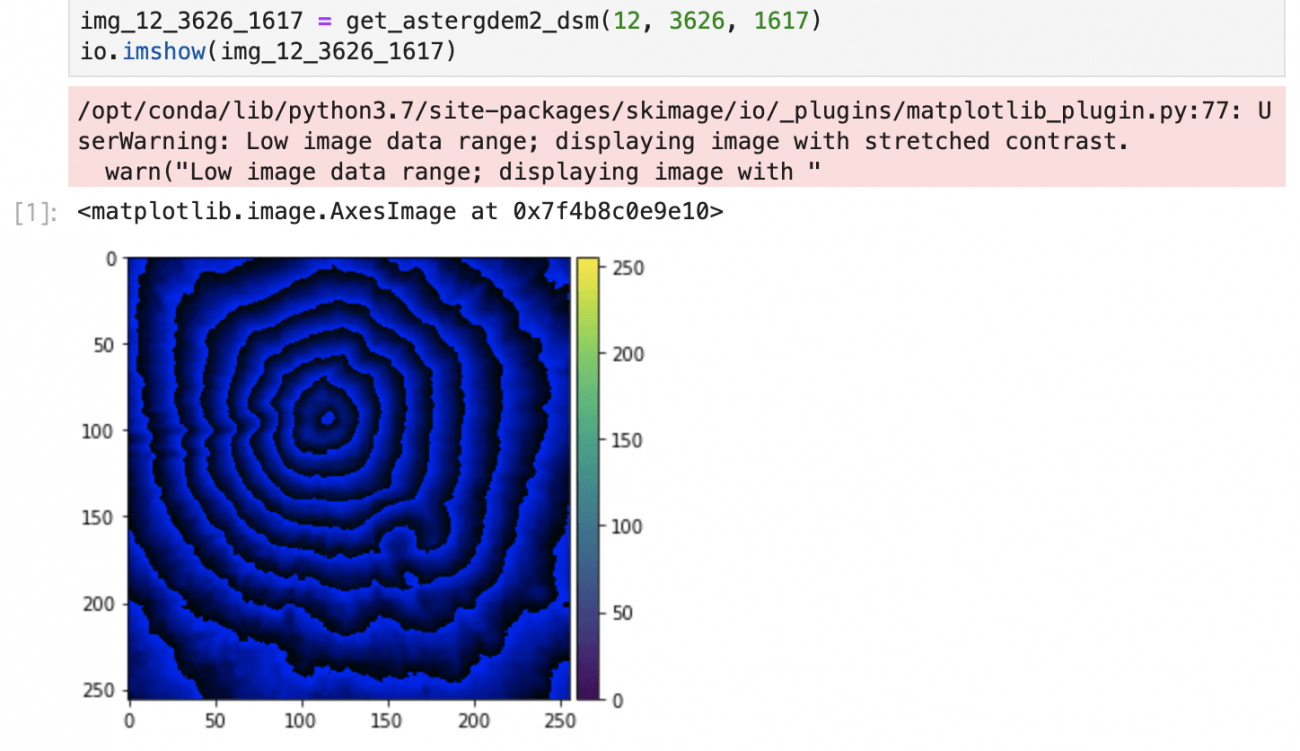
サンプルコードでは富士山の山頂付近の標高タイル(z=12, x=3626, y=161)を取得しています(赤く警告が出る場合がありますが、問題ありません)。
2.富士山の標高を算出しよう
標高は各ピクセルのRGB値から求めることができます。
d = 65536 * R + 256 * G + B
d < 8388608のとき h = d * u d = 8388608のとき h = NA d > 8388608のとき h = (d – 16777216)u
ただし u = 1.0
標高タイルでは海(標高0m)は黒(R=0, G=0, B=0)で表現されます。また、十分な観測ができなかった地点はエラー扱いとなり、赤(R=128, G=0, B=0)で表現されます。
この式を使って、富士山の標高をグラフを作ってみましょう。z=12, x=3626, y=1617のタイルの東経138.73°に相等する列を、緯度方向に走査していきます。
import math
import matplotlib.pyplot as plt
def get_tile_bbox(zoom, topleft_x, topleft_y, size_x=1, size_y=1):
"""
タイル座標からバウンダリボックスを取得
https://tools.ietf.org/html/rfc7946#section-5
"""
def num2deg(xtile, ytile, zoom):
# https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Python
n = 2.0 ** zoom
lon_deg = xtile / n * 360.0 - 180.0
lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * ytile / n)))
lat_deg = math.degrees(lat_rad)
return (lon_deg, lat_deg)
right_top = num2deg(topleft_x + size_x , topleft_y, zoom)
left_bottom = num2deg(topleft_x, topleft_y + size_y, zoom)
return (left_bottom[0], left_bottom[1], right_top[0], right_top[1])
def calc_height_chiriin_style(R, G, B, u=100):
"""
標高タイルのRGB値から標高を計算する
"""
hyoko = int(R*256*256 + G * 256 + B)
if hyoko == 8388608:
raise ValueError('N/A')
if hyoko > 8388608:
hyoko = (hyoko - 16777216)/u
if hyoko < 8388608:
hyoko = hyoko/u
return hyoko
def plot_height(tile, index, direction, z, x, y, xtile_size=1, ytile_size=1, u=1):
"""
高度のグラフをプロットする
Parameters
----------
tile : ndarray
標高タイル
bbox : object
標高タイルのバウンディングボックス
index : number
走査するピクセルのインデックス
direction : number
走査方向(0で上から下、1で左から右)
zoom : number
ズーム率
xtile : number
座標X
ytile : number
座標Y
xtile_size : number
X方向のタイル数
ytile_size : number
Y方向のタイル数
u : number
標高分解能[m](デフォルト 1.0[m])
"""
bbox = get_tile_bbox(z, x, y, xtile_size, ytile_size)
width = abs(bbox[2] - bbox[0])
height = abs(bbox[3] - bbox[1])
if direction == 0:
line = tile[:,index]
per_deg = -1 * height/tile.shape[0]
fixed_deg = width/tile.shape[1] * index + bbox[0]
deg = bbox[3]
title = 'height at {} degrees longitude'.format(fixed_deg)
else:
line = tile[index,:]
per_deg = width/tile.shape[1]
fixed_deg = -1 * height/tile.shape[0] * index + bbox[3]
deg = bbox[0]
title = 'height at {} degrees latitude'.format(fixed_deg)
heights = []
heights_err = []
degrees = []
for k in range(len(line)):
R = line[k,0]
G = line[k,1]
B = line[k,2]
try:
heights.append(calc_height_chiriin_style(R, G, B, u))
except ValueError as e:
heights.append(0)
heights_err.append((i,j))
degrees.append(deg)
deg += per_deg
fig, ax= plt.subplots(figsize=(8, 4))
plt.plot(degrees, heights)
plt.title(title)
ax.text(0.01, 0.95, 'Errors: {}'.format(len(heights_err)), transform=ax.transAxes)
plt.show()
plot_height(img_12_3626_1617, 115, 0, 12, 3626, 1617)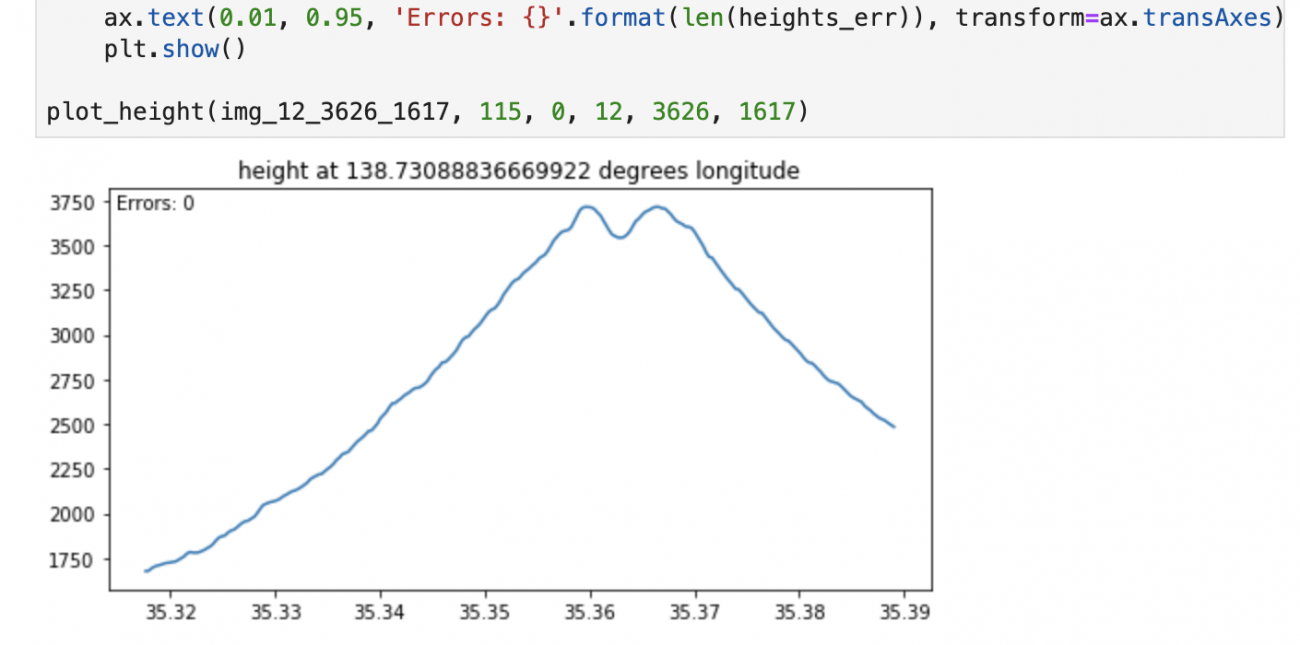
3.世田谷区の標高のばらつきを算出しよう
グラフを作る以外にも標高データを使って遊んでみましょう。
宙畑では以前に公開した記事「QGISで電動アシスト付自転車が売れる町の仮説を立てて実際にその町に行ってみた」で、衛星データから電動アシスト付自転車が売れる町を探りました。
記事ではQGISで東京23区の標高のばらつきを算出していますが、Jupyter LabとASTER GDEM2のデータを使って同じことできるでしょうか。
今回は世田谷区の標高のばらつきを算出することに挑戦してみます。
各区の形状は国土数値情報ダウンロードサービスの行政区域データを利用します。行政区域データのGeoJSONのダウンロード方法はこちらの記事を参考にしてください。
本記事では「work」ディレクトリの下に「data」ディレクトリを作り、そこにGeoJSONをアップロードしています。
このGeoJSONを読み込み、中から自治体コードが13112の要素を抜き出します。
import os
from pathlib import Path
basepath = Path(os.path.expanduser('~'))
filepath = basepath / 'work/data/N03-19_13_190101.geojson'
# ダウンロードした行政区域データを呼び出す
with open(filepath) as f:
df = json.load(f)
# 世田谷区(市区町村コード13112)のfeatureを抜き出す
tokyo_13112_features = [f for f in df['features'] if f['properties']['N03_007']=='13112']
print(len(tokyo_13112_features))
print(tokyo_13112_features[0])

続いて、世田谷区全域が収まるサイズで標高タイルを取得します。ズーム12で縦3枚、横2枚の計6枚をつなぎ合わせます。
import numpy as np
def get_connected_astergdem2_dsm(zoom, topleft_x, topleft_y, size_x=1, size_y=1):
"""
ASTER GDEM2 の標高タイルを size_x * size_y 分つなげた1枚の画像を作る
"""
img = []
for y in range(size_y):
row = []
for x in range(size_x):
row.append(get_astergdem2_dsm(zoom, topleft_x + x, topleft_y + y))
img.append(np.hstack(row))
return np.vstack(img)
tokyo_13112_img = get_connected_astergdem2_dsm(12, 3636, 1612, 2, 3)
io.imshow(tokyo_13112_img)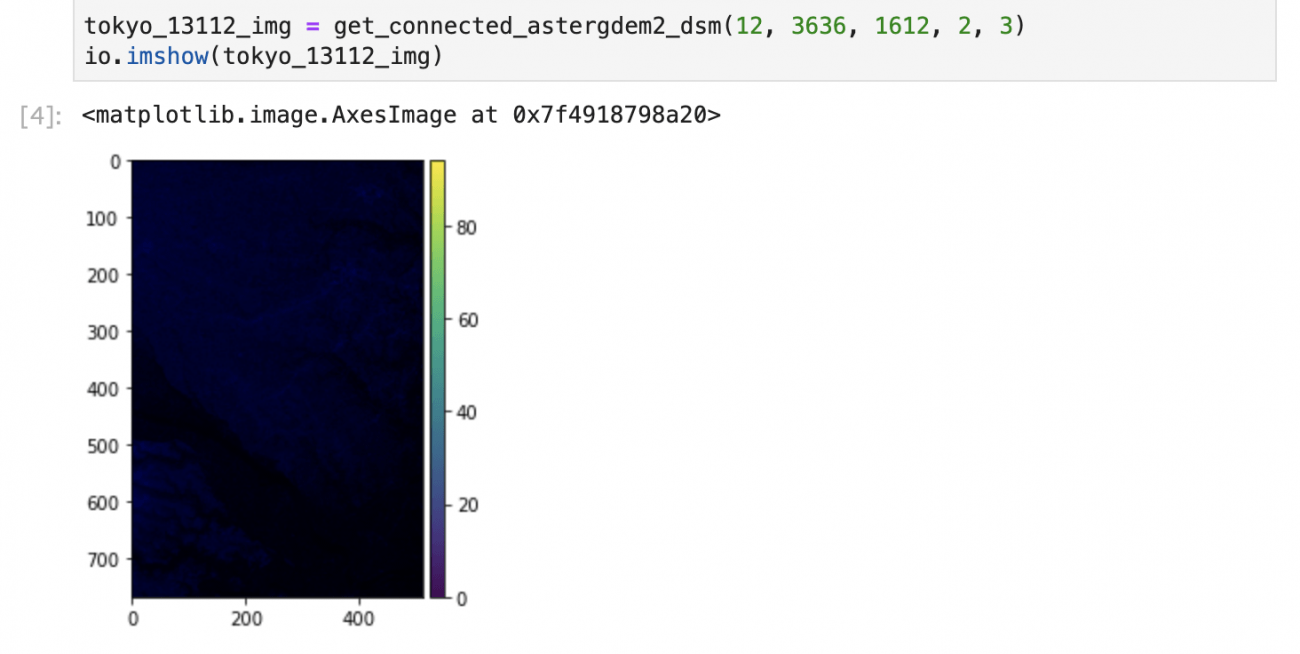
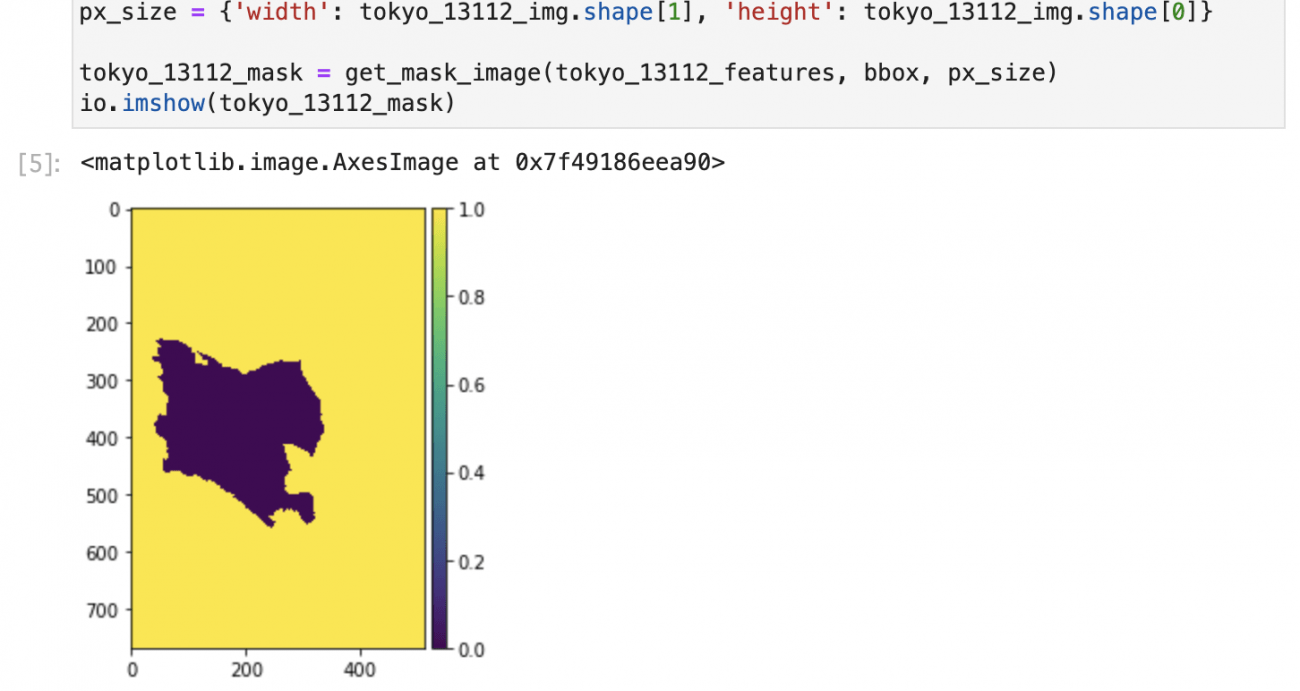
次に、世田谷区のポリゴンから画像作成し、それを重ね合わせることで世田谷区の形状に切り抜かれた標高タイルを作成します。
from skimage.draw import polygon
def get_polygon_image(points, bbox, img_size):
"""
bboxの領域内にpointsの形状を描画した画像を作成する
"""
def lonlat2pixel(bbox, size, lon, lat):
"""
経度緯度をピクセル座標に変換
"""
dist = ((bbox[2] - bbox[0])/size[0], (bbox[3] - bbox[1])/size[1])
pixel = (int((lon - bbox[0]) / dist[0]), int((bbox[3] - lat) / dist[1]))
return pixel
pixels = []
for p in points:
pixels.append(lonlat2pixel(bbox, (img_size['width'], img_size['height']), p[0], p[1]))
pixels = np.array(pixels)
poly = np.ones((img_size['height'], img_size['width']), dtype=np.uint8)
rr, cc = polygon(pixels[:, 1], pixels[:, 0], poly.shape)
poly[rr, cc] = 0
return poly
def get_mask_image(features, bbox, px_size):
"""
図形からマスク画像を作成する
Parameters
----------
features : array of GeoJSON feature object
マスクするfeature objectの配列
bbox : array
描画領域のバウンディングボックス
px_size : array
描画領域のピクセルサイズ
Returns
-------
img_array : ndarray
マスク画像
"""
ims = []
for i in range(len(features)):
points = features[i]['geometry']['coordinates'][0]
ims.append(get_polygon_image(points, bbox, px_size))
mask = np.where((ims[0] > 0), 0, 1)
for i in range(1,len(ims)):
mask += np.where((ims[i] > 0), 0, 1)
return np.where((mask > 0), 0, 1).astype(np.uint8)
bbox = get_tile_bbox(12, 3636, 1612, 2, 3)
px_size = {'width': tokyo_13112_img.shape[1], 'height': tokyo_13112_img.shape[0]}
tokyo_13112_mask = get_mask_image(tokyo_13112_features, bbox, px_size)
io.imshow(tokyo_13112_mask)
def clip_image(img, mask):
"""
図形をマスクする
Parameters
----------
img : ndarray
加工される画像
mask : ndarray
マスク画像
Returns
-------
img_array : ndarray
マスクされた画像
"""
base = img.transpose(2, 0, 1)[:3,:]
cliped = np.choose(mask, (base, 0)).astype(np.uint8)
return cliped.transpose(1, 2, 0)
tokyo_13112_cliped = clip_image(tokyo_13112_img, tokyo_13112_mask)
区の形状に切り抜かれた標高タイルより高さのヒストグラムを作りましょう。
def get_height_array(tile, u):
"""
標高タイルから高さの配列を作る
ただしエラーや0メートル地点は配列から除く
"""
heights = []
heights_err = []
for i in range(tile.shape[0]):
for j in range(tile.shape[1]):
R = tile[i, j, 0]
G = tile[i, j, 1]
B = tile[i, j, 2]
try:
heights.append(calc_height_chiriin_style(R, G, B, u))
except ValueError as e:
heights.append(0)
heights_err.append((i,j))
heights = np.array(heights)
return (heights[heights > 0], heights_err)
def plot_height_hist(tile, u=1):
"""
標高タイルから高さのヒストグラムを作る
Parameters
----------
tile : ndarray
標高タイル
"""
(heights, heights_err) = get_height_array(tile, u)
fig, ax= plt.subplots(figsize=(8, 4))
plt.hist(heights, bins=30, rwidth=0.95)
ax.text(0.01, 0.95, 'Errors: {}'.format(len(heights_err)), transform=ax.transAxes)
plt.show()
plot_height_hist(tokyo_13112_cliped)
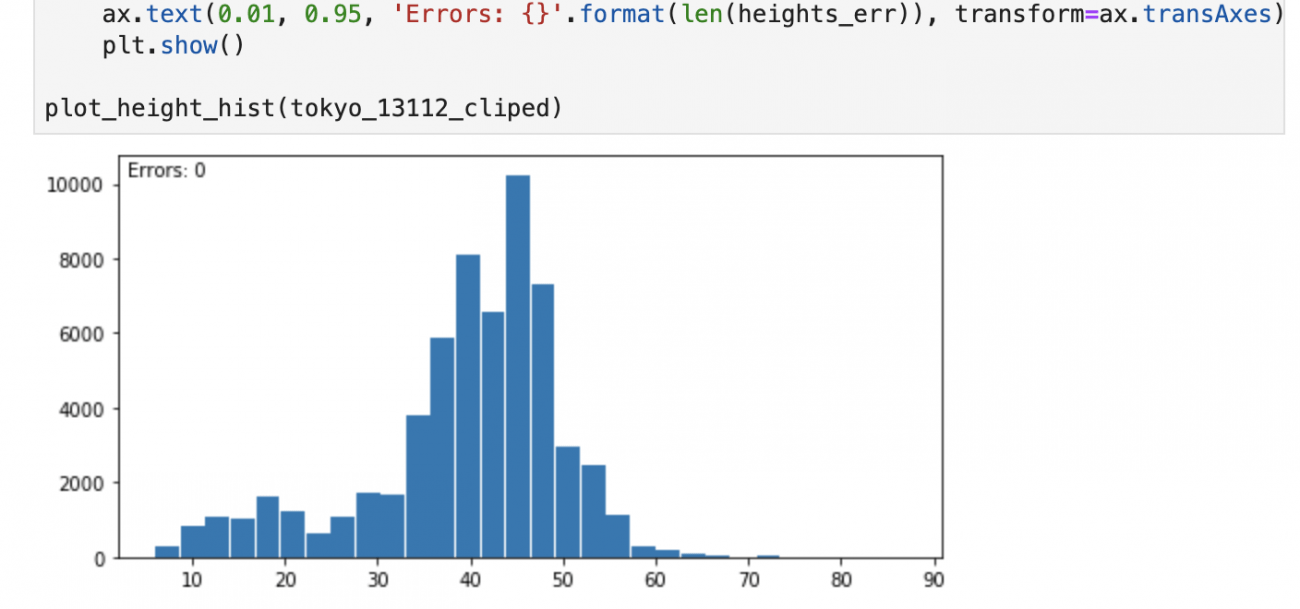
最後に、分散や平均といった統計情報も求めます。
def calc_height_statistics(tile, u=1):
"""
標高タイルの高さの統計情報を求める
Parameters
----------
tile : ndarray
標高タイル
Returns
-------
result_object : object
統計情報
"""
(heights, heights_err) = get_height_array(tile, u)
return {'std': np.std(heights), 'mean': np.mean(heights), 'max': np.max(heights), 'min': np.min(heights)}
print(calc_height_statistics(tokyo_13112_cliped))

算出方法や元となるデータが異なりますが、以前の記事の結果とおおよそ同じ結果を得ることができました。他の区についても同じ要領で求めることができます。
以上が、TellusのJupyter Labで富士山の標高グラフを作成する方法をご紹介しました。ASTER GDEM 2.0のデータは、国土地理院が提供する標高データに精度で劣るものの、データが欠落している範囲が少ないことと、国外の地点もカバーできている点で大変優れているので、ぜひ活用してください。


