以前、宙畑では「富士山が見える範囲を標高データから解析する」という記事を公開しました。

前回の記事では有料のGISツールを使って可視領域を計算しましたが、今回はTellusを使い無料で可視領域を計算してみます。
※記事中で抜粋しながらコードの解説をしますが、とりあえずコードが見たい方は、一番下までスクロールして下さい。

【2020年6月19日追記】
※本記事では、地球の曲率を考慮した計算が入っておらず、皆様から多数のご指摘をいただきました。
修正した記事を以下で公開していますので、こちらをご確認ください。

【計算の仕方】

可視領域を計算するためには、
まず観測点から対象地点が見えるかどうかを計算します。（Intervisibility：相互視認性）

観測点から対象地点を見た時に視線を遮るものがなければ、
その地点から対象物が見えます。（当たり前ですが笑）

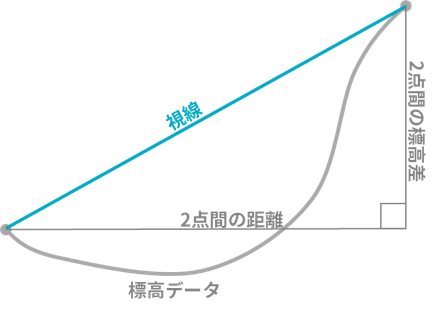
視線は、2点間の距離と標高差が分かれば三角関数を使い計算できます。

遮蔽物の有無は、Tellus上で利用できる標高データ（ASTER GDEM 2.0) を使えば確認できます。

標高データについてはこちらの記事（【ゼロからのTellusの使い方】Jupyter Labで富士山の標高グラフを作成する）を参照下さい。

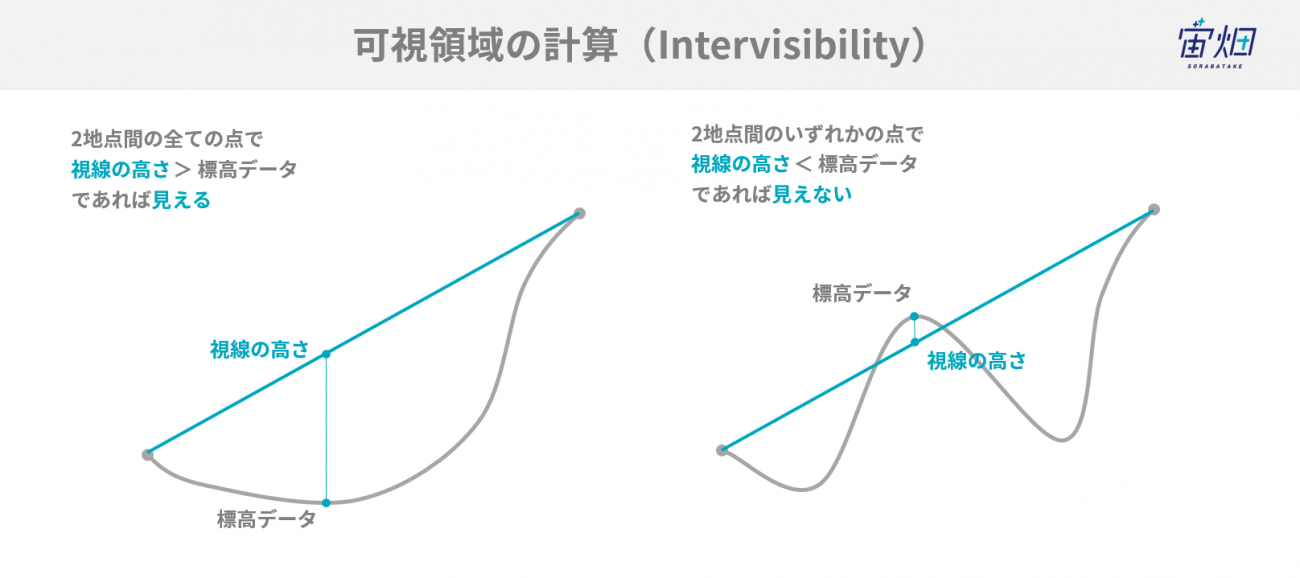
なので、2点間の標高データと計算した視線を比較し、
標高データが視線の高さより低ければ、見える。標高データが視線の高さより高ければ、障害物に阻まれて見えない、ことを確認できます。

①下準備

【観測点・対象点の設定】

観測点と対象点を緯度・経度指定します。
今回 Intervisibilityを測定する2点（樫野埼灯台（和歌山県串本町) 、 富士山）

#富士山
lon1=138.701921
lat1=35.341138

#樫野埼灯台
lon2=135.860882
lat2=33.471744

【標高データのタイルを取得】

下の関数を使い標高タイルを取得します。始点となるタイルを、タイル座標で指定し、縦横に連結するタイル数を指定します。樫野埼灯台（和歌山県串本町) – 富士山の間は 34でした。

##始点（左上）となるタイルを指定           
z=12
x=3593
y=1617

##縦横に連結するタイルの個数
c=34

##タイルを取得
combined_img = get_combined_image(get_astergdem2_dsm, z, x, y, c)
io.imshow(combined_img)

コード内で使用している関数 get_astergdem2_dsm と get_astergdem2_dsmは、下の記事に詳しく書いてあるので参考にして下さい。

②単位の変換

【取得したタイルの左上角の座標（始点）を取得】

今後、単位の変換（例：世界ピクセル座標 ⇆ タイル内ピクセル座標）をするのに、取得したタイルの左上角の座標（始点）が必要です。それを求めます。

まずタイル座標の緯度経度を取得する関数を用意します。

def num2deg(x, y, z):
  n = 2.0 ** z
  lon_deg = x / n * 360.0 - 180.0
  lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * y / n)))
  lat_deg = math.degrees(lat_rad)
  return (lat_deg, lon_deg)

下記のコードをお借りしました。

https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Tile_numbers_to_lon./lat._2

この関数は引数に ( x、y、z ) を指定することで、タイルの左上の角の緯度経度を返します。

この関数で、始点となるタイル左上の角の緯度経度を取得します。

left_top_bbx = num2deg(x, y, z)

#出力結果
print(left_top_bbx)
(135.791015625, 35.389049966911664)

次に、緯度経度を世界ピクセル座標に変換する関数を用意します。

def latlon2tile2(lon, lat, z):
    L = 85.05112878
    x = int((lon/180 + 1) * 2**(z+7))
    y = int( (2**(z+7) / pi * ( -arctanh(sin(pi*lat/180)) + arctanh(sin(pi*L/180)) ) ))
    
    return [y, x]

下記のコードをお借りしました。

https://qiita.com/kobakou/items/4a5840542e74860a6b1b

始点を世界ピクセル座標に変換します。

left_top_bbx_px = latlon2tile2(left_top_bbx[0], left_top_bbx[1], z)

#実行結果
print(left_top_bbx_px)
[413952, 919808]

【観測点と対象点のタイル内ピクセル座標を取得】

観測点と対象点も世界ピクセル座標に変換します。

px1_wpx = latlon2tile2(lon1, lat1, z)
px2_wpx = latlon2tile2(lon2, lat2, z)

世界ピクセル座標を、タイル内ピクセル座標に変換します。

def worldpx2tilepx(worldpx,left_top_bbx_px):
    y1 = worldpx[0] - left_top_bbx_px[0] -1
    x1 = worldpx[1] - left_top_bbx_px[1] -1
    return [y1,x1]
px1_tpx = worldpx2tilepx(px1_wpx,left_top_bbx_px)
px2_tpx = worldpx2tilepx(px2_wpx,left_top_bbx_px)
y1 = px1_tpx[0]
x1 = px1_tpx[1]
y2 = px2_tpx[0]
x2 = px2_tpx[1]

#実行結果
print(y1,x1)
print(y2,x2)
170 8477
6770 202

③2点間の標高データ（遮蔽物）を取得

【2点間の傾きを計算】

2点間のかたむきを取得する関数を用意します。

def get_radian_btw_p1p2(y1, x1, y2, x2):
    """
    2点間のかたむき(y=ax)を取得する
    Parameters
    ----------
    y1 : number 
        点Aのy座標
    x1 : number 
        点AのX座標
    y2 : number 
        点Bのy座標
    x2 : number 
        点BのX座標
    Returns
    -------
    radian : number
        かたむき
    """
    
    "0で割ると division by zero エラーが出る"
    if (x2 - x1) == 0:
        return "vertical"
    elif (y2 - y1) == 0:
        return "horizontal"
    else:
        return (y2 - y1) / (x2 - x1)

この関数では、1次関数 のかたむきの式 (y2 – y1) / (x2 – x1) を使いかたむきを求めます。
かたむきが、垂直か水平の場合はそれぞれのフラグを返します。

【2点を結ぶ、傾きXの直線上のタイルを取得】

2点間の標高データを取得する関数を用意します。

def get_heights_btw_p1p2(tile, y1, x1, y2, x2, radian):
    """
    始点から終点を結ぶ直線上の、標高データを取得
    一次関数：y = ax + b
    
    Parameters
    ----------
    tile : ndarray
        標高タイル
    y1 : number 
        点Aのy座標
    x1 : number 
        点AのX座標
    radian : number 
        傾き
    Returns
    -------
    actual_heights : ndarray
        x1y1を通り、かたむきradian上の標高データ
    """
    if radian == "vertical":
        return tile[:,y1]
    elif radian == "horizontal":
        return tile[x1,:]
    
    """
    原点を設定
    ---
    x座標が小さい点をoriginに設定
    """
    if x1 <= x2:
        origin_y = y1
        origin_x = x1
        point_y = y2
        point_x = x2
    else:
        origin_y = y2
        origin_x = x2
        point_y = y1
        point_x = x1
        
    max_index = len(tile) -1
    radian_tile = []
    
    while (round(origin_y) <= max_index and round(origin_x) <= max_index) and (round(origin_y) != point_y or round(origin_x) != point_x):
        """
        round関数で平均化
        """
        radian_tile.append(tile[round(origin_y),round(origin_x)])
        origin_y += radian
        origin_x += 1

    return np.array(radian_tile)

この関数では引数に与えられた、始点と終点から原点を判別し、原点に「x座標 + 1」 「y座標 + かたむき ] をするループを回します。

そのxy座標を2次元配列である標高タイルデータのIndexとして使用することで、2点間を結ぶ直線上の標高データを取得しています。

この関数を使い、2点間の標高を取得します。

actual_heights = get_heights_btw_p1p2(combined_img, y1, x1, y2, x2, radian)
plot_height(actual_heights)

※ コード中の plot_height は取得した標高をJupyterNotebook にグラフ表示する関数です。

④2点間の視線を計算

今後の計算をしやすくする為に、x座標が小さい点をorigin_x, orign_yという変数に代入します。

if x1 <= x2:
    origin_y = y1
    origin_x = x1
    point_y = y2
    point_x = x2
else:
    origin_y = y2
    origin_x = x2
    point_y = y1
    point_x = x1

【高さを計算】

標高タイルから観測点と対象点のカラーコードを取得します。
取得したカラーコードを標高に変換します。

#2点のカラーコードを取得
origin_color = combined_img[origin_y][origin_x]
point_color = combined_img[point_y][point_x]

#2点の標高を取得（単位:m）
u=1
origin_height = calc_height_chiriin_style(origin_color[0],origin_color[1],origin_color[2],u)
point_height = calc_height_chiriin_style(point_color[0],point_color[1],point_color[2],u)

※ calc_height_chiriin_styleはカラーコードを標高に変関する関数です。calc_height_chiriin_styleはこちらの記事でも使用しています。

2点の標高差を取得（単位:m）

標高差を取得します。

diffrence_height_p1p2 = abs(origin_height - point_height)

【底辺を計算】

観測点と対象点の距離をピタゴラスの定理を使って計算します。

distance_btw_p1p2 = get_distance_btw_p1p2(y1, x1, y2, x2)
def get_distance_btw_p1p2(y1, x1, y2, x2):
    side_a = abs(y1 - y2)
    side_b = abs(x1 - x2)
    side_c2 = (side_a ** 2) + (side_b ** 2)
    return sqrt(side_c2)

タイルの解像度（m）を計算
先ほど取得した2点間の距離の単位は、pxの個数なので、単位がmの高さ（2点間の標高差）とそのまま計算ができません。

なので、解像度（1pxあたり何mか）を計算します。

avarage_lat = (lat1 + lat2) / 2
resolution = abs(get_resolution(avarage_lat,z))
def get_resolution(lat,zoom):
    """
    引数で指定されたZoomレベルと緯度の時、1pxは何mかを返す
    https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Resolution_and_Scale
    Parameters
    ----------
    latitude : number
        緯度
    zoomlevel : number 
        ズームレベル
    Returns
    -------
    resolution : number
        （meters/pixel）
    """
    return (156543.03 * cos(lat) / (2 ** zoom))

参考
https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Resolution_and_Scale

距離（ピクセル）× 解像度（m）を計算。距離の単位をmに変換します。

distance_btw_p1p2_meter = distance_btw_p1p2 * resolution

【tanθを計算】

高さと底辺から三角関数を使いtanθを計算します。これで 底辺がX(m)の時の、高さY(m)が解ります。

tan_p1p2 = get_tan(diffrence_height_p1p2,distance_btw_p1p2_meter)
def get_tan(height,bottom_side):
    """
    高さと底辺からtanθを取得
    Parameters
    ----------
    height : number 
        ab点の標高差
    bottom_side : number 
        ab間の距離
    Returns
    -------
    tan : number
        heightとbottom_sideを辺とする直角三角形のtanθ
    """
    return height/bottom_side

視線を表す直角三角形を計算
上で求めた、高さ、底辺、tanθを使い直角三角形系を計算します。この時、標高データの配列の要素数を使い、標高と視線の底辺の長さが揃うようにします。

calc_heights = get_calc_height(tan_p1p2,distance_btw_p1p2_meter,origin_height,point_height,actual_heights)
plot_calc_height(calc_heights)

def get_calc_height(tan, distance, origin_height, point_height, actual_heights):
    
    if origin_height <= point_height:
        origin_is_lower = True
    else:
        origin_is_lower = False
    
    lower_height = origin_height if origin_is_lower else point_height
    
    calc_heights = []
    check_scale = distance/len(actual_heights)
    last_index = len(actual_heights)
    
    for index in range(last_index):
        if not origin_is_lower:
            index = last_index - index
        check_distance = index * check_scale
        height = (tan * check_distance) + lower_height
        calc_heights.append(height)
        
    return calc_heights

※ plot_calc_height は、グラフに計算した視線を描画するための関数です。

⑤標高データ（遮蔽物）と直角三角形の高さを比較（視線）

標高データ要素数で視線の直角三角形の底辺を分割し分割した要素を足した地点で、標高と視線の高さを比較します。

視線の高さが、標高より高い場合には、可視性はTrueを、低い場合にはFalseを出力します。

check_Intervisibility(actual_heights,calc_heights)
def check_Intervisibility(actual_heights,calc_heights,u=1):
    """
    任意の2点の標高を比較。標高高い順番に配列形式で返す。
    """
    index = 0
    actual_height = 0
    calc_height=0

    for index in range(len(actual_heights)):
        
        print("-------------------------------")
        print("index " + str(index))
        actual_height = calc_height_chiriin_style(actual_heights[index][0],actual_heights[index][1],actual_heights[index][2],u)
        print("Actual " + str(actual_height) + "m")
        
        #LOSに身長170cmを追加
        human_height = 1.7
        calc_height = calc_heights[index]
        print(calc_height)
        print("LOS " + str(calc_heights[index] + human_height)+ "m (include human height 170cm)")
        
        if calc_height + human_height >= actual_height:
            print("Result See")
        else:
            print("Result Can't see")
            break;
        index += 1

⑤実験（求めてみた）

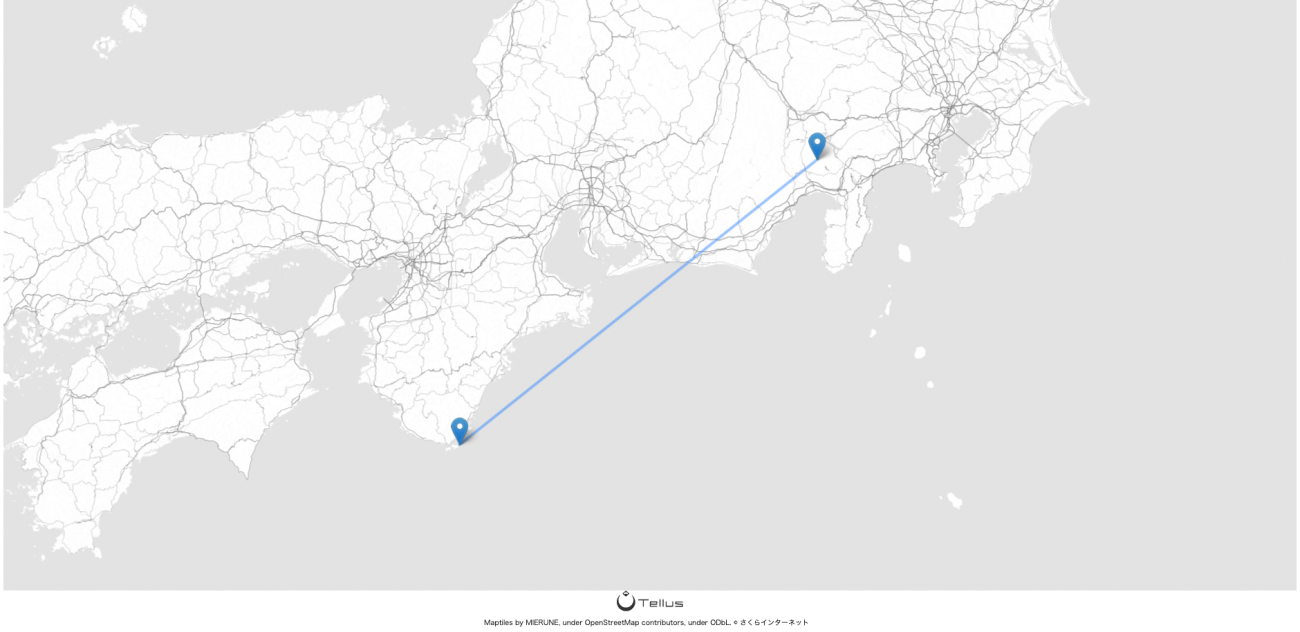
前回の記事内では、富士山の可視領域に大島が入っていました。ちょうど 大島にある樫野埼灯台（和歌山県串本町) あたりが、可視領域です。

なので、樫野埼灯台から富士山が見えるか、Tellus上で実験してみます。

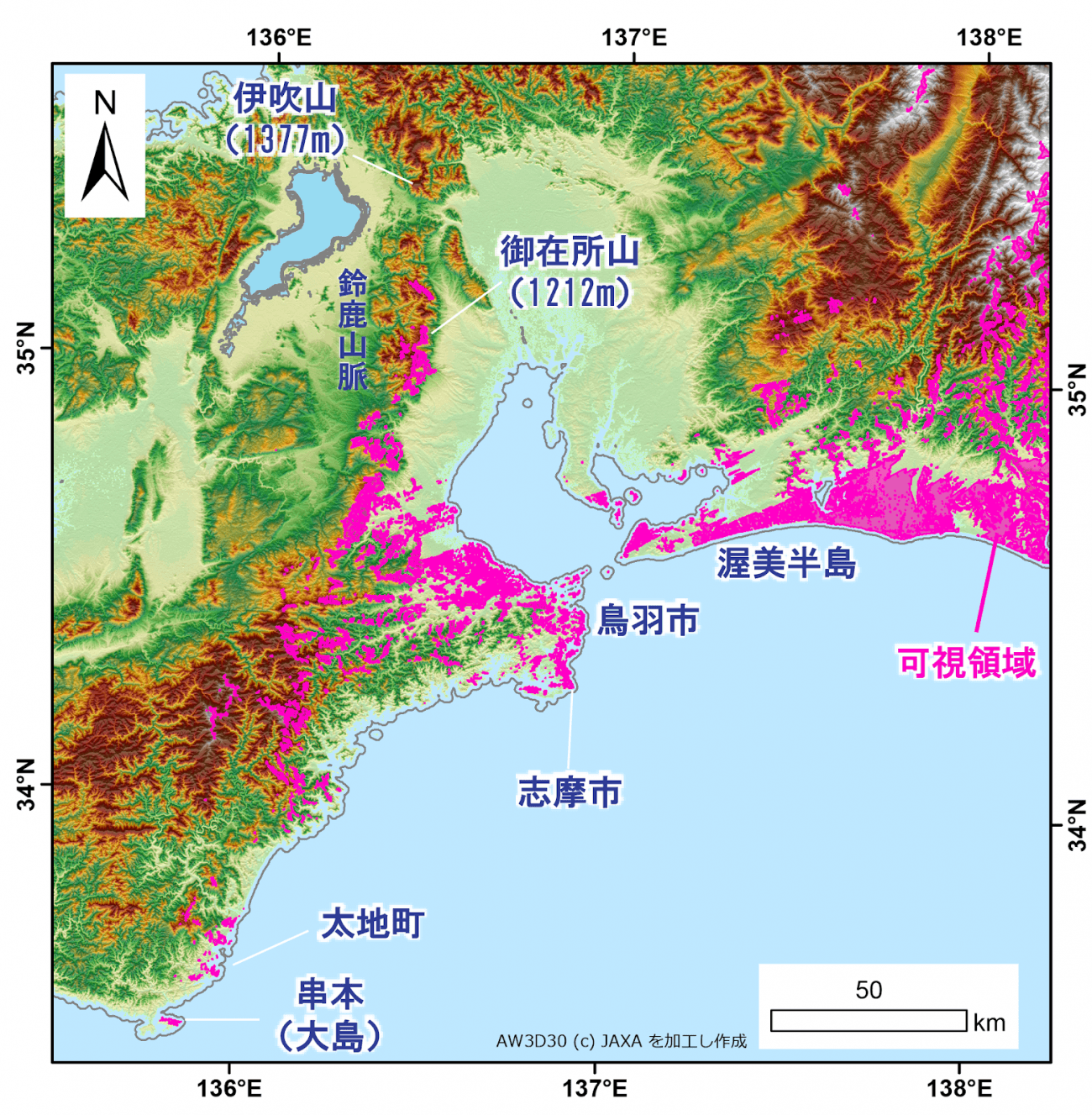
結果：

1. 樫野埼灯台 – 富士山
前回の記事と同じく、樫野埼灯台から富士山が見えるという結果が出ました。
ただ、これだけでは計算式の妥当性が分かりません。なので可視領域外の点を、観測点に再計算してみます。

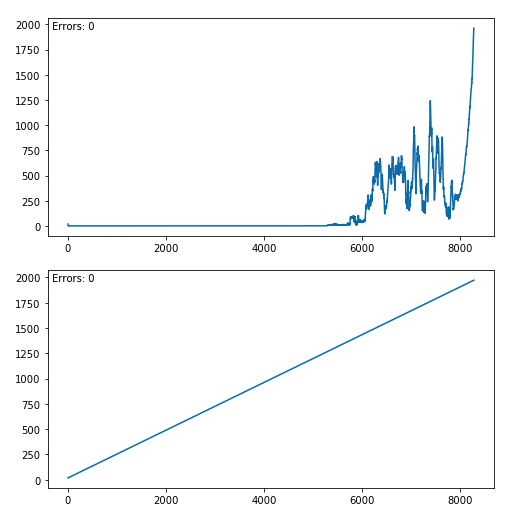
2. 串本町（不可視領域） – 富士山

不可視領域のポイントからは、富士山が見えないという結果出ました。なので計算式は妥当と思われます。

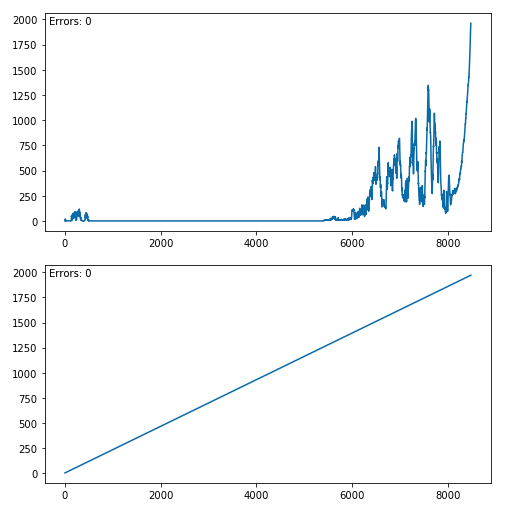
検証の結果、前回と同じく樫野埼灯台（大島）からは富士山は見え、不可視領域からは見えないということが分かりました。おおよそ妥当な結果になったと思います。

この計算を、検証したい範囲の地点に対して行なうと可視領域が計算できます。

ただ、地点が多すぎると計算時間とパワーがとてつもなく必要になりますので、

この記事内では一旦ここまでとします。

⑥検証

では、本当に樫野埼灯台から富士山が見えるのか、検証してみたいと思います。

【ヒアリング・ネット調査】

串本町在住の方に聞いてみたのですが、「樫野埼灯台から富士山が見える」という情報は聞いたことがないそうで、インターネットで情報を検索してみても、Googleストリートビューを確認しても、そういった情報を見つけることはできませんでした。

今度串本町に行った際にはぜひ確認したいと思います。

【国土地理院地図との比較】

国土地理院が提供している、断面図を可視化するツールを使って検証もしてみました。

https://maps.gsi.go.jp/

座標 35.341138,138.701921（富士山）と 33.471744,135.860882（樫野埼灯台）を結ぶ線の GeoJsonを、上のURLを開き、右上のツール > 断面図からインポートします。

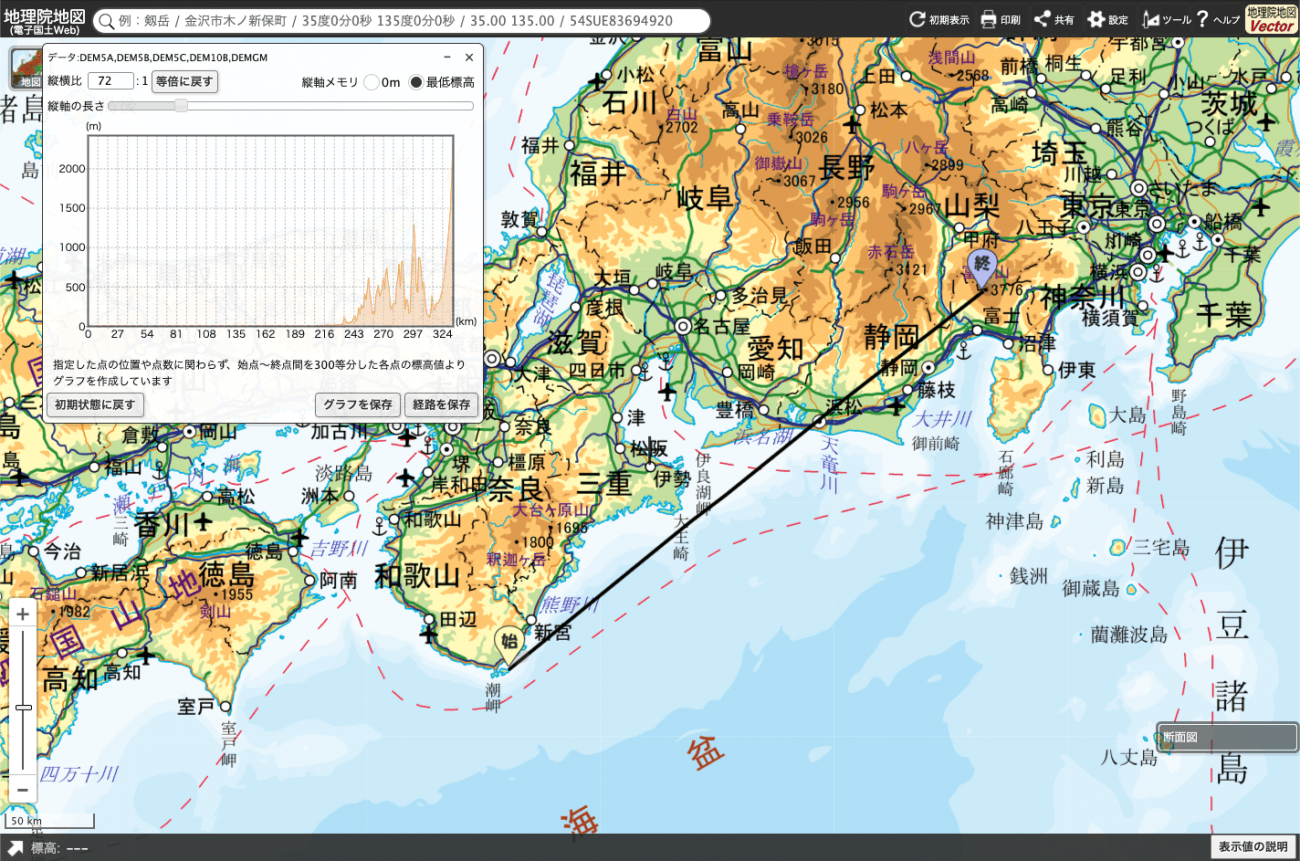
すると以下のように断面図の標高をグラフ出力してくれます。

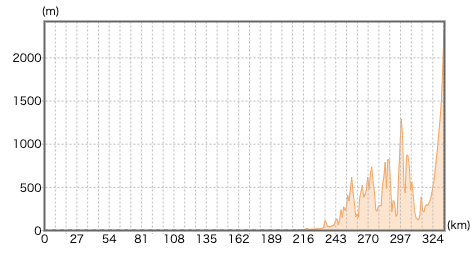
結果を、目視で比較するとほぼ同じに見えました。
なのでおそらく妥当な計算結果かなと思われます。

⑦考えられる本コードの適用例

今回は富士山をの可視地点を計算しましたが、他にも対象物を変えて応用可能です。
宙畑編集部内で出たアイデアを参考までにリストアップしておきます。

– 有名な花火大会の打ち上げ場所と打ち上げの高さを想定して、花火が見える家がどこにあるのか？を探す。
– 通天閣や東京タワーなど街のシンボルになる高い建造物がどこから見えるか？
– 展望台から見える夜景をシミュレーションする

他にもアイディアがあれば、どんどんチャレンジしてみてください！

「Tellus」で無料の衛星データを触ってみよう！

日本発のオープン＆フリーなデータプラットフォーム「Tellus」で、まずは衛星データを見て、触ってみませんか？

★Tellusの利用登録はこちらから

⑧コード全文

import requests, json
import numpy as np
from numpy import arctanh
from skimage import io
from io import BytesIO
import math
from math import pi
from math import tanh
from math import sin
from math import asin
from math import sqrt
from math import cos
import matplotlib.pyplot as plt
%matplotlib inline

TOKEN = 'YOUR-TOKEN'

def get_combined_image(get_image_func, z, topleft_x, topleft_y, size=1):
    """
    結合されたタイル画像を取得する
    Parameters
    ----------
    get_image_func : function 
        タイル画像取得メソッド
        引数はz, x, y, option, params
    z : int 
        タイルのズーム率 
    topleft_x : int 
        左上のタイルのX座標 
    topleft_y : int 
        左上のタイルのY座標 
    size_x : int 
         タイルを経度方向につなぎわせる枚数 
    size_y : int 
        タイルを緯度方向につなぎわせる枚数
    option : dict 
        APIパスのオプション(z,x,y除く)
    params : dict 
        クエリパラメータ
    Returns
    -------
    combined_image: ndarray
        結合されたタイル画像
    """
    rows = []
    blank = np.zeros((256, 256, 4), dtype=np.uint8)
    
    for y in range(size):
        row = []
        for x in range(size):
            try:
                img = get_image_func(z, topleft_x + x, topleft_y + y)
            except Exception as e:
                img = blank
                
            row.append(img)
        rows.append(np.hstack(row))
    return  np.vstack(rows)

def get_astergdem2_dsm(zoom, xtile, ytile):
    """
    ASTER GDEM2 の標高タイルを取得

    Parameters
    ----------
    zoom : str 
        ズーム率 
    xtile : str 
        座標X 
    ytile : number 
        座標Y
    Returns
    -------
    img_array : ndarray
        標高タイル(PNG)
    """
    url = " https://gisapi.tellusxdp.com/astergdem2/dsm/{}/{}/{}.png".format(zoom, xtile, ytile)
    headers = {
        "Authorization": "Bearer " + TOKEN
    }
    
    r = requests.get(url, headers=headers)
    return io.imread(BytesIO(r.content))


def latlon2tile2(lon, lat, z):
    """
    指定した緯度経度からピクセル座標を取得
    https://qiita.com/kobakou/items/4a5840542e74860a6b1b
    """
    L = 85.05112878
    x = int((lon/180 + 1) * 2**(z+7))
    y = int( (2**(z+7) / pi * ( -arctanh(sin(pi*lat/180)) + arctanh(sin(pi*L/180)) ) ))
    
    return [y, x]

def num2deg(xtile, ytile, zoom):
    # https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Python
    """
    この関数は引数に ( x、y、z ) を指定することで、タイルの左上の角の緯度経度を返します。
    他にも、xとy の両方もしくは片方に、+1 した引数を指定すると別の角の座標を取得でき、
    +0.5 で中央の座標を取得できます。
    """
    n = 2.0 ** zoom
    lon_deg = xtile / n * 360.0 - 180.0
    lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * ytile / n)))
    lat_deg = math.degrees(lat_rad)
    return (lon_deg, lat_deg)

def get_radian_btw_p1p2(y1, x1, y2, x2):
    """
    2点間のかたむき(y=ax)を取得する
    Parameters
    ----------
    y1 : number 
        点Aのy座標
    x1 : number 
        点AのX座標
    y2 : number 
        点Bのy座標
    x2 : number 
        点BのX座標
    Returns
    -------
    radian : number
        かたむき
    """
    
    "0で割ると division by zero エラーが出る"
    if (x2 - x1) == 0:
        return "vertical"
    elif (y2 - y1) == 0:
        return "horizontal"
    else:
        return (y2 - y1) / (x2 - x1)

def get_heights_btw_p1p2(tile, y1, x1, y2, x2, radian):
    """
    始点から終点を結ぶ直線上の、標高データを取得
    一次関数：y = ax + b
    
    Parameters
    ----------
    tile : ndarray
        標高タイル
    y1 : number 
        点Aのy座標
    x1 : number 
        点AのX座標
    radian : number 
        傾き
    Returns
    -------
    actual_heights : ndarray
        x1y1を通り、かたむきradian上の標高データ
    """
    if radian == "vertical":
        return tile[:,y1]
    elif radian == "horizontal":
        return tile[x1,:]
    
    """
    原点を設定
    ---
    x座標が小さい点をoriginに設定
    """
    if x1 <= x2:
        origin_y = y1
        origin_x = x1
        point_y = y2
        point_x = x2
    else:
        origin_y = y2
        origin_x = x2
        point_y = y1
        point_x = x1
        
    max_index = len(tile) -1
    radian_tile = []
    
    while (round(origin_y) <= max_index and round(origin_x)  8388608:
        hyoko = (hyoko - 16777216)/u
    if hyoko < 8388608:
        hyoko = hyoko/u
    return hyoko

def get_calc_height(tan,distance):
    """
    b点からdistance進んだ時の、斜辺の高さ
    Parameters
    ----------
    tan : number
        tanθ
    distance : number 
        任意の距離b点からの距離
    Returns
    -------
    height : number
        b点からdistance進んだ時の、斜辺の高さ
    """
    return tan * distance

def get_resolution(lat,zoom):
    """
    引数で指定されたZoomレベルと緯度の時、1pxは何mかを返す
    https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Resolution_and_Scale
    Parameters
    ----------
    latitude : number
        緯度
    zoomlevel : number 
        ズームレベル
    Returns
    -------
    resolution : number
        （meters/pixel）
    """
    return (156543.03 * cos(lat) / (2 ** zoom))

def plot_height(actual_heights, u=1):
    """
    高度のグラフをプロットする
    """
    heights = []
    heights_err = []

    for k in range(len(actual_heights)):
        R = actual_heights[k,0]
        G = actual_heights[k,1]
        B = actual_heights[k,2]
        try:
            heights.append(calc_height_chiriin_style(R, G, B, u))
        except ValueError as e:
            heights.append(0)
            heights_err.append((i,j))
            
    fig, ax= plt.subplots(figsize=(8, 4)) 
    plt.plot(heights)
    ax.text(0.01, 0.95, 'Errors: {}'.format(len(heights_err)), transform=ax.transAxes)
    plt.show()
    
def get_calc_height(tan, distance, origin_height, point_height, actual_heights):
    """
    任意の2点を通る直角三角形の、高度のグラフをプロットする
    """
    
    if origin_height = actual_height:
            print("Result See")
        else:
            print("Result Can't see")
            break;
        index += 1

#---------------------------------------------#

#手順説明
print("やっているコト")
print("1. 二点の座標を結ぶ直線上の標高を取得。")
print("2. 二点の標高差を「高さ」距離を「底辺」とした直角三角形から、LOS（Line of Sight）を計算。")
print("3. 1と2を比較し、1が2を上回る場合は。Intervisibilityは真とする。")

#---------------------------------------------#

#実際の標高を取得
#2点を結ぶ直線上の標高をタイルから取得。

##始点（左上）となるタイルを指定           
z=12
x=3593
y=1617

##縦横に連結するタイルの個数
c=34

##タイルを取得
combined_img = get_combined_image(get_astergdem2_dsm, z, x, y, c)
io.imshow(combined_img)

## Intervisibilityを測定したい2点を指定（緯度・経度）
###富士山
raw1 = [35.341138,138.701921]
lon1=raw1[1]
lat1=raw1[0]

# 場所: 34.7079707, 135.2386603

# raw2 = [33.484788,135.789550] #串本
raw2 = [33.471744,135.860882] #大島
lon2=raw2[1]
lat2=raw2[0]

##始点の世界ピクセル座標を取得
left_top_bbx = num2deg(x, y, z)
left_top_bbx_px = latlon2tile2(left_top_bbx[0], left_top_bbx[1], z)

##観測点と対象点の世界ピクセル座標を取得
px1_wpx = latlon2tile2(lon1, lat1, z)
px2_wpx = latlon2tile2(lon2, lat2, z)

##観測点と対象点のタイル内ピクセル座標を取得
px1_tpx = worldpx2tilepx(px1_wpx,left_top_bbx_px)
y1 = px1_tpx[0]
x1 = px1_tpx[1]
px2_tpx = worldpx2tilepx(px2_wpx,left_top_bbx_px)
y2 = px2_tpx[0]
x2 = px2_tpx[1]

##2点間のかたむきを取得
radian = get_radian_btw_p1p2(y1, x1, y2, x2)

##2点間の標高データを取得（単位:m）
actual_heights = get_heights_btw_p1p2(combined_img, y1, x1, y2, x2, radian)
plot_height(actual_heights)

#---------------------------------------------#
#LOS（Line of Sight）を計算
#2点間の、標高差を「高さ」距離を「底辺」とする直角三角形を計算。

"""
原点を設定
---
x座標が小さい点をoriginに設定
"""
if x1 <= x2:
    origin_y = y1
    origin_x = x1
    point_y = y2
    point_x = x2
else:
    origin_y = y2
    origin_x = x2
    point_y = y1
    point_x = x1
        
#2点のカラーコードを取得
origin_color = combined_img[origin_y][origin_x]
point_color = combined_img[point_y][point_x]

#2点の標高を取得（単位:m）
u=1
origin_height = calc_height_chiriin_style(origin_color[0],origin_color[1],origin_color[2],u)
point_height = calc_height_chiriin_style(point_color[0],point_color[1],point_color[2],u)

#2点の標高差を取得（単位:m）
diffrence_height_p1p2 = abs(origin_height - point_height)

#測定したい2点間の距離を取得（単位:px）
distance_btw_p1p2 = get_distance_btw_p1p2(y1, x1, y2, x2)

##タイルの解像度を取得(m/px)
#TODO resolutionが国土地理院のサイトの計算結果と違うので要検討
avarage_lat = (lat1 + lat2) / 2
resolution = abs(get_resolution(avarage_lat,z))

#2点の距離と標高差から、直角三角形のtanθを取得（単位:m）
distance_btw_p1p2_meter = distance_btw_p1p2 * resolution
tan_p1p2 = get_tan(diffrence_height_p1p2,distance_btw_p1p2_meter)

#---------------------------------------------#
#2点間の標高と、距離と標高差から作成した直角三角形の高さを比較
calc_heights = get_calc_height(tan_p1p2,distance_btw_p1p2_meter,origin_height,point_height,actual_heights)
plot_calc_height(calc_heights)

#Intervisibilityをチェック
check_Intervisibility(actual_heights,calc_heights)