1.はじめに

衛星から夜の地球を観測したデータは「夜間光データ」と呼ばれており、GDP(国内総生産)と強い相関があることから経済指標の一つとして扱われています。

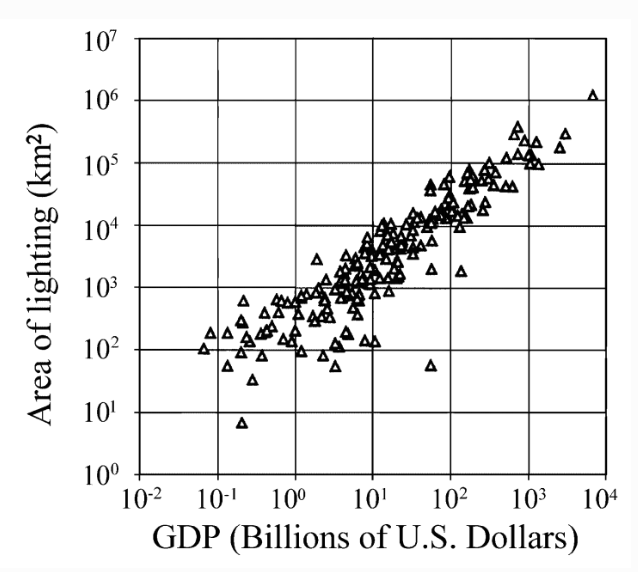
それならば国の自治体レベル(市区町村)の経済指標とも相関があるのか、調査をしてみることにしました。GDPは国内総生産と近い自治体レベルの経済指標として、自治体ごとの総収入額が挙げられますが、本記事では自治体の財政の余裕さを表す「財政力指数」を扱うこととします。単純に収入が多いだけでなく、財政が余裕な地域がわかると移住先の検討の参考にもできるのではと考えました。

本記事では機械学習を使って夜間光画像から各自治体の財政力指数の予測が可能かを検証しています。
検証の流れとして、まずは市区町村ごとの「夜間光データから抽出した特徴量」と「財政力指数」のデータセットを作成。そのデータセットに対して、線形回帰モデルとランダムフォレストを適用して、夜間光データから財政力指数の予測が可能かの検証を行います。

2.扱うデータ

本章では今回扱うデータについてそれぞれ説明します。

2.1.夜間光データ

代表的な夜間光データのひとつが、アメリカの衛星であるSuomi-NPPに搭載されているVisible/Infrared Imager and Radiometer Suite(VIIRS)によって撮影されたものです。こちらのデータは海洋と大気に関する調査および研究をするNOAA(National Oceanic and Atmospheric Administration:アメリカ海洋大気庁)によって提供されてます。

夜間光のデータは、撮影したタイミングで雲がかかっていたり、稲妻やオーロラが発生していると正しく地域の光量を観測することができません。そこでNOAAでは、VIIRSの画像を月間もしくは年間で集約することで雲などのノイズを除去した夜間光データを作成してくれています。

VIIRSは地上分解能が500 m程度と通常の光学データに比べて粗いですが、上述の通り月間・年間でのノイズの除去された夜間光データとして配信されているため、よく利用されています。

夜間光データについては、宙畑でもこれまでに紹介してきている記事がありますのでぜひご覧ください。

2.2.財政力指数

各自治体の経済指標として、財政力指数があります。

財政力指数とは、「地方公共団体の財政力を示す指数で、基準財政収入額を基準財政需要額で除して得た数値の過去3年間の平均値」です。 財政力指数が高いほど、財源に余裕がある自治体であると言えます。

各自治体の財政力指数は総務省のサイト(https://www.soumu.go.jp/iken/zaisei/R03_chiho.html)で公開されています。こちらからエクセルをダウンロードし、使用するデータのみを抽出してcsvで保存して使用します。

今回使用するのは、市区町村コード、市区町村名、財政力指数のため、Excelで以下の処理を手動で行いました。
・「団体コード」を「市区町村コード」に記載変更
・都道府県名と団体名をマージした「市区町村名」の列を作成
・市区町村コード、市区町村名、財政力指数以外の列を削除

※今回は必要なデータの抽出とcsv化は手動で行いましたが、自動化しておくと今後新年度の財政力指数のデータセットを作成するときに便利です。

2.3.ポリゴンデータ

ポリゴンデータとは、簡単に言えば緯度経度を持った形状のデータのことで、日本の市区町村ごとのポリゴンデータは国土交通省のサイトからダウンロードすることができます。サイトからダウンロードした全国の市区町村のポリゴンデータはGeoPandas等で読み込むことができます。
https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-N03-v3_0.html

3.夜間光データから取得する特徴量

機械学習では「特徴量」の抽出が重要になります。そもそも機械学習とは、大量のデータをもとに法則やパターンを見つけること。法則やパターンを見つける際に、着目すべきデータの特徴を表す変数が特徴量です。

例えば、機械学習の有名な練習問題の一つに「あやめの分類」があります。公開されているデータセットでは、特徴量として「ガクの長さ」「ガクの幅」「花弁の長さ」「花弁の幅」があります。それらを使用して「setosa種」「versicolor種」「virginica種」に分類する問題です。

ここでは特徴量は4つのみとなっていますが、他にも「花弁の色」「花弁の厚さ」「茎の太さ」などの特徴量も考えられ、それぞれ分類するために意味があったりなかったりすると思われます。

このようにあるデータ(あやめ)から、どのような特徴量を抽出するか(できるか)をまず検討し、機械学習による予測を行う必要があります。

本記事では、夜間光画像とポリゴンデータから取得する特徴量を以下5つとします。

1.合計値(sumLight)
市区町村ごとの光量の合計値です。合計値が大きければ、財政的に豊かというように正の相関関係があると考えられます。

2.平均値(meanLight)
市区町村ごとのpixelあたりでの光量の平均値です。今回使用するVIIRSは解像度が約500mのため、500m×500mあたりでの光量の平均値となります。広い市区町村で一部の地域が明るく、その他の地域が暗いといった場合は平均値は小さくなるため、財政力指数と一概に正の相関関係があるとはいえなさそうです。

3.最大値(maxLight)
市区町村ごとの光量の最大値です。光量が大きいということは、光が密集していると考えられるため、それだけ栄えており財政的にも豊かというように、正の相関関係があると考えられます。

4.ばらつき(lightStd)
市区町村ごとの光量の標準偏差です。地域全体が明るい場合はばらつきは小さく、偏りがある場合はばらつきが大きくなります。直感的には全体が明るければ、それだけ財政的に豊かとなりそうです。

5.面積
市区町村ごとの面積です。夜間光画像とは関係はありませんが、ポリゴンデータから取得可能であり、面積が大きければ人が多く住めるため、財政的にも豊かになる可能性もあるため、今回は特徴量として加えてみました。

4.市区町村ごとの財政力指数/ポリゴンデータのデータフレームの作成

続いて、市区町村ごとの財政力指数とポリゴンデータを持つデータフレームを作成します。

まずは使用するライブラリをimportします。

# Google ColabとGoogle Driveを使用する場合は以下のコメントアウトを外して、ライブラリのインストールとGoogle Driveのマウントを実行してください。

# 必要なライブラリをインストール
# !pip -q -q -q install earthengine-api geopandas
# !pip -q -q -q install datapackage
# !pip install rasterio
# !pip install japanize-matplotlib

# Google Driveのマウント
# from google.colab import drive
# drive.mount('/content/drive')

import geopandas as gpd
import datapackage
import pandas as pd
import ee
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
import rasterio
from scipy import stats
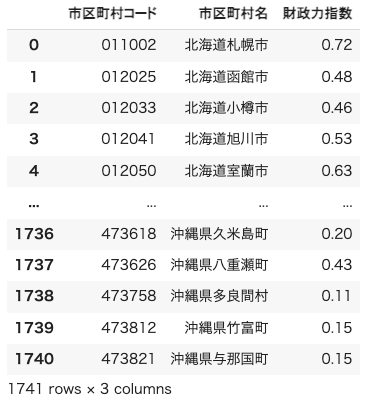
from concurrent.futures import ThreadPoolExecutor, as_completed

2.2項で作成した財政力指数のcsvをpandasで読み込みます。

fci = pd.read_csv('2.2項で作成したcsvのファイルパスを貼り付けてください', dtype=str)

fci

以下のように読み込むことができました。

市区町村コードの末尾の1桁は後のポリゴンデータとの結合時に不要となるため、削除しておきます。

# 市区町村コードの末尾を削除する
fci["市区町村コード"] = fci["市区町村コード"].str[:-1]
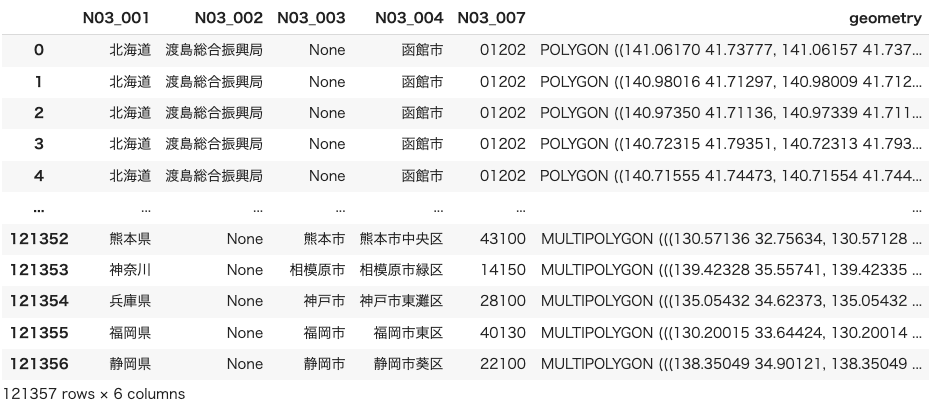
fci

国土交通省のサイトからダウンロードした全国の市区町村のポリゴンデータをGeoPandasで読み込みます。

geo = gpd.read_file('2.3項でダウンロードしてきたgeojsonのファイルパスを貼り付けてください', encoding='cp932')
geo

全国の市区町村ごとのポリゴンデータが取得できました。

この後、財政力指数のデータフレームとポリゴンデータのデータフレームを結合します。
しかし、ポリゴンデータは行政区単位にデータが分かれていますが、財政力指数は分かれていません。

例えば、下図のように財政力指数のデータフレームでは札幌市として一つのデータを持っていますが、ポリゴンデータのデータフレームでは札幌市◯◯区とより詳細なエリアに別れてデータを持っています。

そもそも行政区とは、「政令指定都市に条例で設けられている区」のことで、大きな都市の市民の利便性と行政能率の向上を目的として設置されているものです。財政自体は市として管理されるため、財政力指数のデータフレームは行政区で分かれていません。

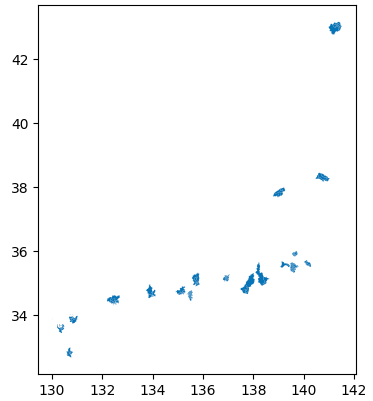
よって、この2つのデータフレームを結合するためには、まずポリゴンデータのデータフレームのうち、行政区に分かれているデータを1つの市のデータとして結合する必要があります。行政区のデータは、”N03_003″カラムの末尾が「市」かつ”N03_004″カラムの末尾が「区」となっているため、そのようなデータを抽出します。

# 行政区を抽出
gyoseiku_geo = geo[(geo["N03_003"].str.endswith("市")) & (geo["N03_004"].str.endswith("区"))]
gyoseiku_geo.plot()

抽出したデータを見てみると、全国の政令指定都市が抽出されたことがわかります。

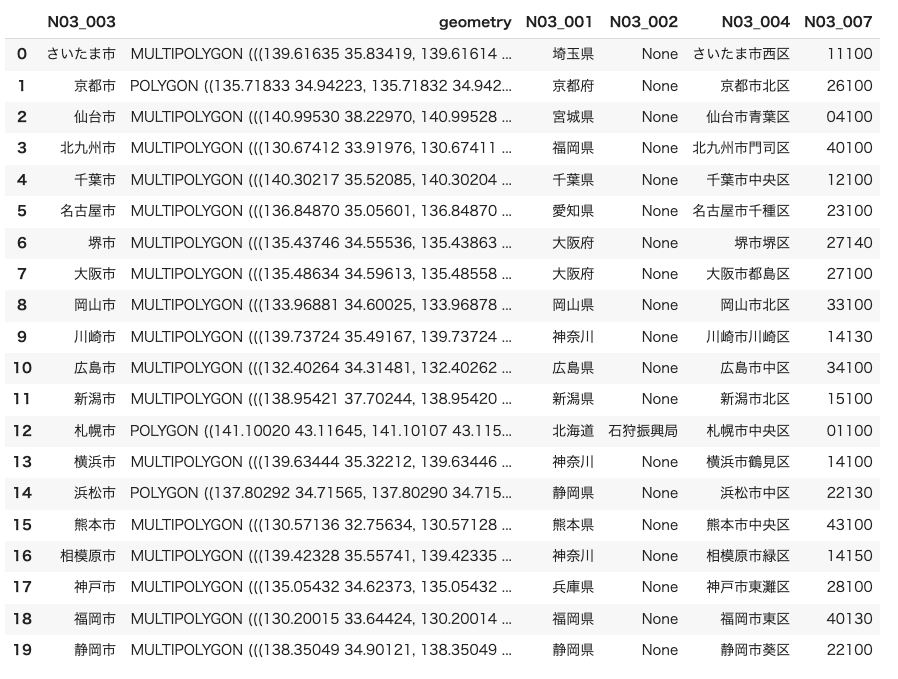
次に”N03_003″カラムが同じものを結合することで、行政区に分かれているデータを1つの「市」のデータにまとめます。

このような場合はGeoPandasの.dissolve()を適用することでデータを結合できます。

# 行政区をまとめて、行政区域コードを書き換える
# 行政区をまとめた市は末尾を"0"とする
gyoseiku_dissolved = gyoseiku_geo.dissolve(by="N03_003")
gyoseiku_dissolved = gyoseiku_dissolved.reset_index()
gyoseiku_dissolved["N03_007"] = gyoseiku_dissolved["N03_007"].str.replace(r'.$', '0', regex=True)
gyoseiku_dissolved

行政区をまとめることができました。

元のポリゴンデータのデータフレームから行政区のデータを削除し、先ほど作成した行政区を1つの「市」にまとめたデータフレームと結合します。

# 行政区の行を削除する。
condition = (geo["N03_003"].str.endswith("市")) & (geo["N03_004"].str.endswith("区"))
filtered_geo = geo[~condition]

# 行政区をまとめたデータフレームと、行政区を取り除いたデータフレームを結合する
df = pd.concat([filtered_geo, gyoseiku_dissolved], ignore_index=True)
df

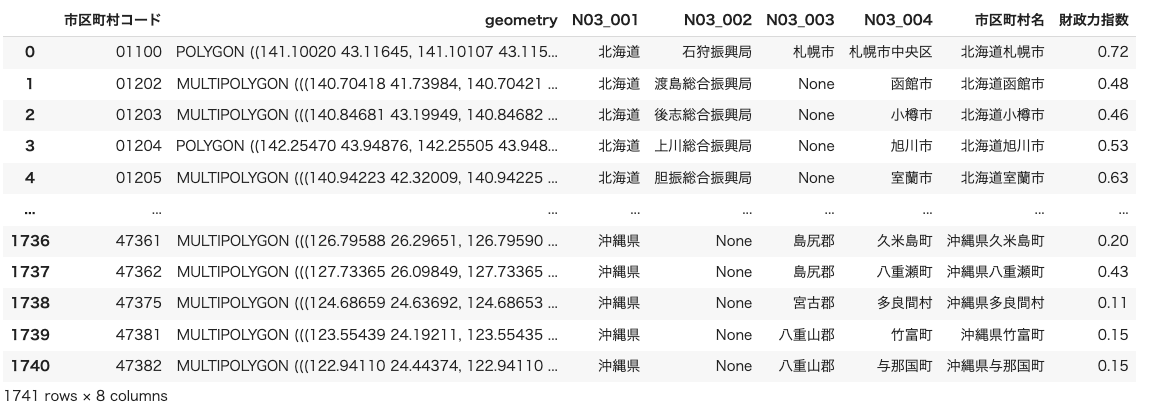
最後にポリゴンデータのデータフレームに.dissolve()を適用します。これは飛び地のある行政区域があるためです。これらを1つのポリゴンデータにまとめるためにデータを結合する必要があります。また、財政力指数のデータフレームと結合するためにカラム名を揃えておきます。

# dissolvedする。
dissolved = df.dissolve(by="N03_007")
dissolved = dissolved.reset_index()
dissolved

# 財政力指数のデータフレームと結合するためにカラム名を変更する
dissolved.rename(columns={"N03_007": "市区町村コード"}, inplace=True)
dissolved

財政力指数のデータフレームとポリゴンデータのデータフレームを結合します。

data = dissolved.merge(fsi, on="市区町村コード", how="inner")
data

市区町村ごとのポリゴンデータと財政力指数を持つデータフレームが作成できました。

最後に、ポリゴン数が1000以上のある市区町村をデータフレームから削除します。ポリゴン数が多い市区町村に対しては、後ほど行う衛星データを使った解析がタイムアウトしてしまうためです。

# 'geometry'列にMultipolygonを持つ行をフィルタリング
multipolygons = data[data['geometry'].geom_type == 'MultiPolygon']

# ポリゴン数が1000未満の行を抽出
filtered_data = multipolygons[multipolygons['geometry'].apply(lambda geom: len(geom.geoms) > 1000)]

# Multipolygonでない行も含めた全体のデータフレームを取得
filtered_data = data[~data.index.isin(filtered_data.index)]
filtered_data

5.夜間光-財政力指数データセットの作成

衛星データはGoogle Earth Engineを利用します。GEEの認証とモジュールのインポートを行います。GEE認証を実行すると認証に必要なURLが表示されるので、URLへアクセスしてGoogleアカウントを指定し、表示された認証コードをGoogle Colabのボックスへコピペしてください。

# Google Earth Engineの初期化
try:
    ee.Initialize()
except Exception as e:
    ee.Authenticate()
    ee.Initialize()

2.1項で紹介したVIIRSのデータのうち、2022年のデータを取得します。

# VIIRSのデータを取得
start_year = 2022
end_year = 2022

viirs = ee.ImageCollection("NOAA/VIIRS/DNB/MONTHLY_V1/VCMSLCFG")
viirs = viirs.filter(ee.Filter.calendarRange(start_year, end_year, "year")).select("avg_rad").median()

GeoPandasからGEEで扱う形式のgeometryを作成する関数を定義します。

# GeoPandasのgeometryからGEEのgeometryに変換する関数
def get_aoi(code, df):
    poly = df.loc[df['市区町村コード']==code, 'geometry'].values[0]
    if poly.geom_type =='MultiPolygon':
        g = [geom for geom in poly.geoms]
    else:
        g = [poly]
    features = []
    for i in range(len(g)):
        x,y = g[i].exterior.coords.xy
        coords = np.dstack((x,y)).tolist()
        features.append(coords)
    aoi = ee.Geometry.MultiPolygon(features)
    return aoi

与えられた画像とgeometryから以下の値を取得する関数を定義します。
・合計値
・最大値
・平均値
・標準偏差(ばらつき)
・geometryの面積

# 合計光量を得る関数
def get_sumlight(img, aoi):
  sum = img.reduceRegion(reducer=ee.Reducer.sum(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
  return sum

# 平均光量を得る関数
def get_meanlight(img, aoi):
  mean = img.reduceRegion(reducer=ee.Reducer.mean(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
  return mean

# 最大値を得る関数
def get_maxlight(img, aoi):
  max = img.reduceRegion(reducer=ee.Reducer.max(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
  return max

# 光量のばらつきを得る関数
def get_light_std(img, aoi):
    std = img.reduceRegion(reducer=ee.Reducer.stdDev(), geometry=aoi, scale=463.83, maxPixels=1e9).get('avg_rad').getInfo()
    return std

# 面積を得る関数
def get_area(aoi):
    area = aoi.area().getInfo()
    return area

上で定義した5つの関数をまとめて呼び出す関数を定義します。

# 特徴量の計算
def get_features(collection, aoi):
    sum = get_sumlight(collection, aoi)
    mean = get_meanlight(collection, aoi)
    max = get_maxlight(collection, aoi)
    light_std = get_light_std(collection, aoi)
    area = get_area(aoi)

    return sum, mean, max, area, light_std

計算結果を格納するデータフレームを作成します。

# 結果を格納するDataFrameの準備
columns = ['code', 'fsi', 'sumLight', 'meanLight', 'maxLight', 'area', 'lightStd']
dataset = pd.DataFrame(columns=columns)

計算を実行します。VIIRSのデータと各市区町村毎のポリゴンデータから特徴量を取得し、データフレーム(dataset)に格納していきます。

下のコードではThreadPoolExecutorを用いて複数の市区町村の計算を同時に行うコードとなっていますが、それでも長い時間を要するので注意してください。ThreadPoolExecutorはスレッドプールを利用して並行処理を行うための仕組み。複数のスレッドを最初に起動し、各スレッドで計算を実行させ、計算が終わったものから結果を取得する方式です。

これにより各国データに対して「compute_features」メソッドを並行して処理することができ、処理時間短縮ができます。

# 特徴量の計算を実行する関数
def compute_features(code):
    aoi = get_aoi(code, data)
    sum, mean, max, area, light_std = get_features(viirs, aoi)
    fsi = data.loc[data['市区町村コード'] == code, '財政力指数'].values[0]
    return {'code': code, 'fsi': fsi, 'sumLight': sum, 'meanLight': mean, 'maxLight': max, 'area': area, 'lightStd': light_std}

# df_polyとdf_gdpの両方に存在する国のISO_A3コードのリストを作成
countries = filtered_data['市区町村コード'].tolist()

with ThreadPoolExecutor(max_workers=5) as executor:
    future_to_features = {executor.submit(compute_features, code): code for code in countries}
    for future in as_completed(future_to_features):
        features = future.result()
        tmp_df = pd.DataFrame(features.values(), index=features.keys()).T
        dataset = pd.concat([dataset, tmp_df], axis=0, ignore_index=True)

dataset

各市区町村毎の財政力指数と夜間光画像から取得した特徴量を持つデータセットを作成することができました。

6.機械学習の適用

6.1.データセットの観察

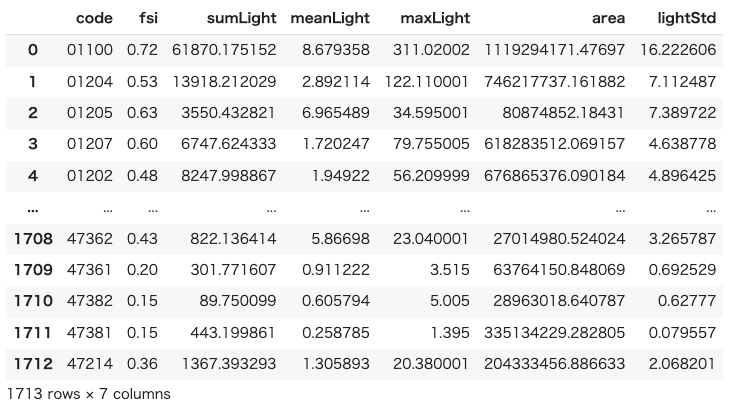
まずは作成したデータセットの観察をしてみます。夜間光データから作成した特徴量と財政力指数の散布図をプロットします。

features = [col for col in dataset.columns if col not in ['code','fsi']]

fig, axes = plt.subplots(len(features) // 3 + len(features) % 3, 3, figsize=(15, 15))
fig.tight_layout(pad=5.0)

for ax, feature in zip(axes.ravel(), features):
    sns.scatterplot(data=dataset, x=feature, y='fsi', ax=ax)
    plt.xticks(np.arange(0, 1.1, step=0.2))
    ax.set_title(f'{feature} vs fsi')
    ax.set_xlabel(feature)
    ax.set_ylabel('fsi')

# 余分なサブプロットを非表示にする
for remaining_ax in axes.ravel()[len(features):]:
    remaining_ax.axis('off')

plt.show()

平均値(meanLight)、最大値(maxLight)、ばらつき(lightStd)については、おおよそ右肩あがりの関係になっているため正の相関があるようにも見えます。

平均値、最大値に比例しそうということはなんとなく事前のイメージがつきますが、ばらつきともそのような関係がありそうなのは意外ですね。

また、夜間光データではありませんが特徴量として加えた面積（area）についてはどちらかといえば右肩下がりの関係になっているため負の相関が見られそうです。

また、最大値のグラフでは赤枠で囲ったあたりのデータは、その他のデータに比べて大きく離れた位置にあり、外れ値となっていそうです。

6.2.外れ値の除外

グラフをみると、外れ値があり、予測に影響を与えてしまう可能性があるため、外れ値を除外していきます。標準偏差からしきい値を決め、そこから外れている値は削除していきます。今回はしきい値=1σ分にしています。

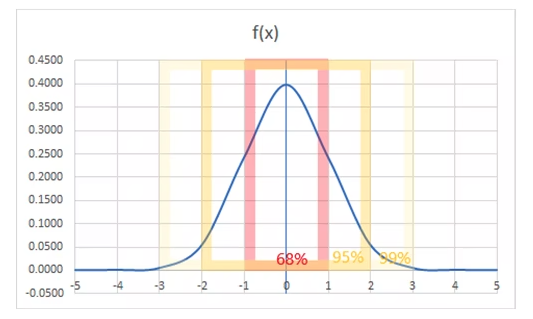
※しきい値=1σ分について
平均値を中央にして、標準偏差に従い正規化された形で分布を見るものを正規分布曲線といいます。標準偏差で出力される値を「σ」 (シグマ) で表した場合、1σ には約 68%、2σ には約 95%、3σ には約 99% のデータが含まれていると考えるものが正規分布です。(引用サイト)

今回は以下のグラフの1σ分(68%)部分のデータのみ使用し、端の方のデータを削除しました。

# オブジェクト型の列を数値型に変換
dataset[features] = dataset[features].apply(pd.to_numeric, errors='coerce')

# NaN（変換できなかった値）を除去
dataset.dropna(subset=features, inplace=True)

# Z-Scoreを計算(Z=(X-μ)/σ X:個々のデータ点, μ:データセットの平均, σ:標準偏差)
z_scores = np.abs(stats.zscore(dataset[features]))

# 閾値を設定（σと同義）
threshold = 1

# 外れ値を含まない行だけを抽出
dataset = dataset[(z_scores < threshold).all(axis=1)]

# indexをリセット
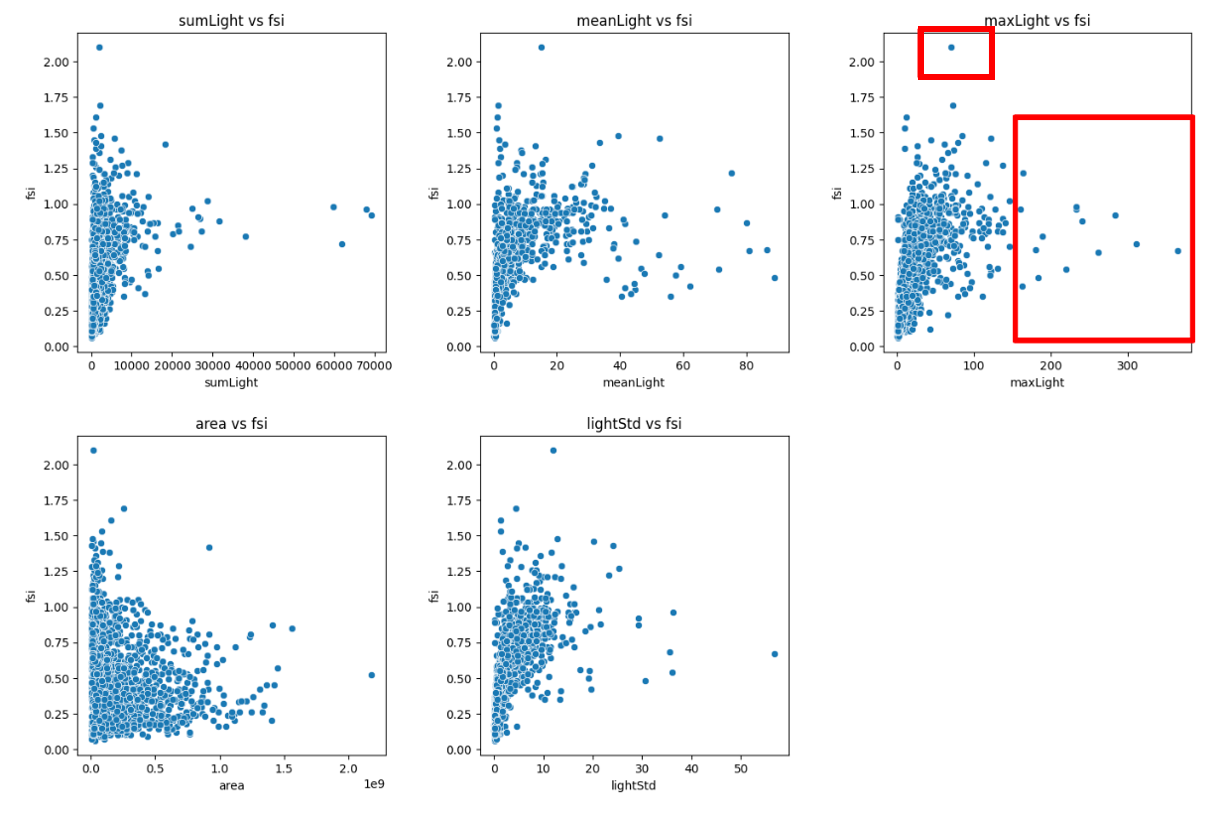
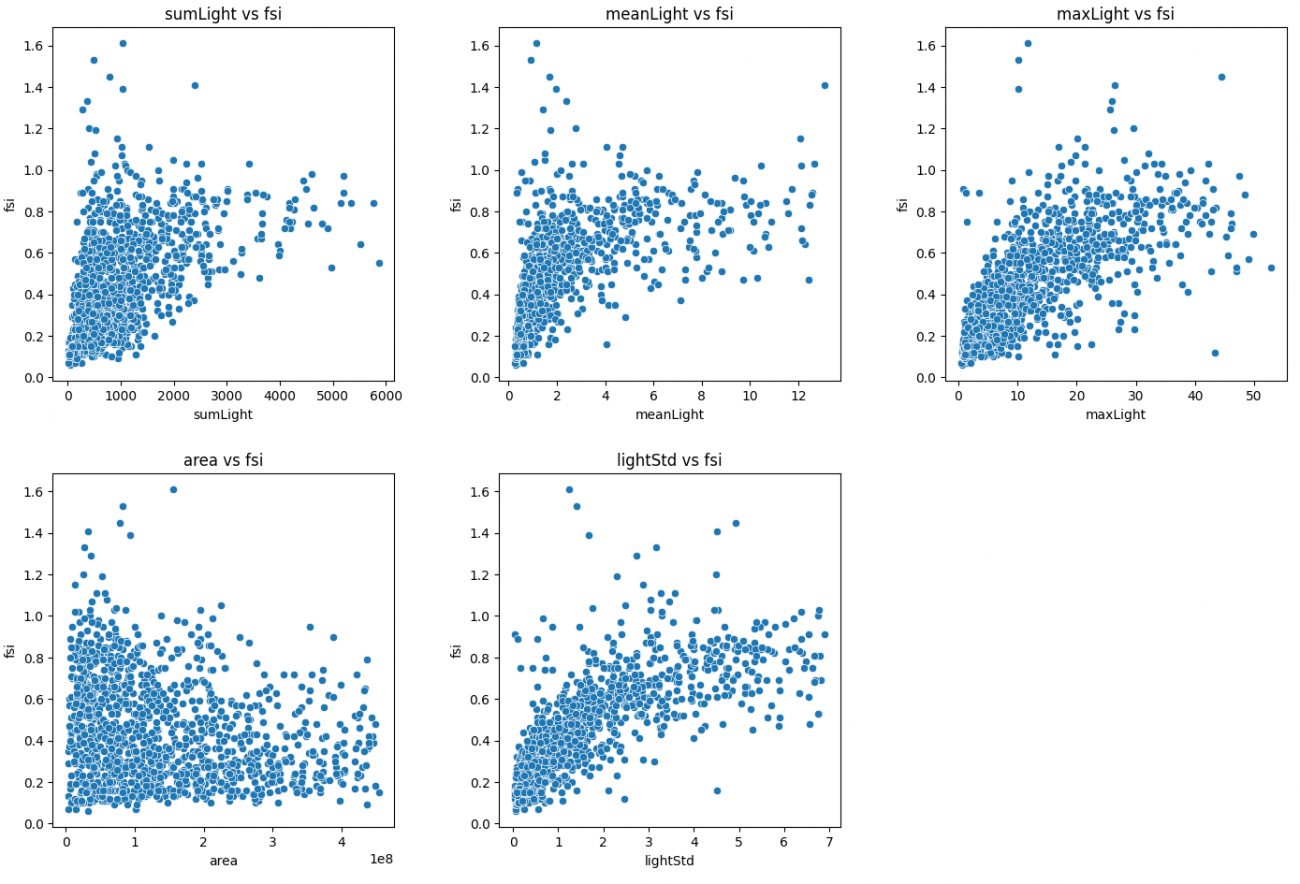
dataset.reset_index(inplace=True, drop=True)

先ほどと同じコードで散布図を表示してみると、やはり平均値、最大値、ばらつきは正の相関がありそうです。また、合計値(sumLight)も同じく正の相関がありそうなことがわかりました。

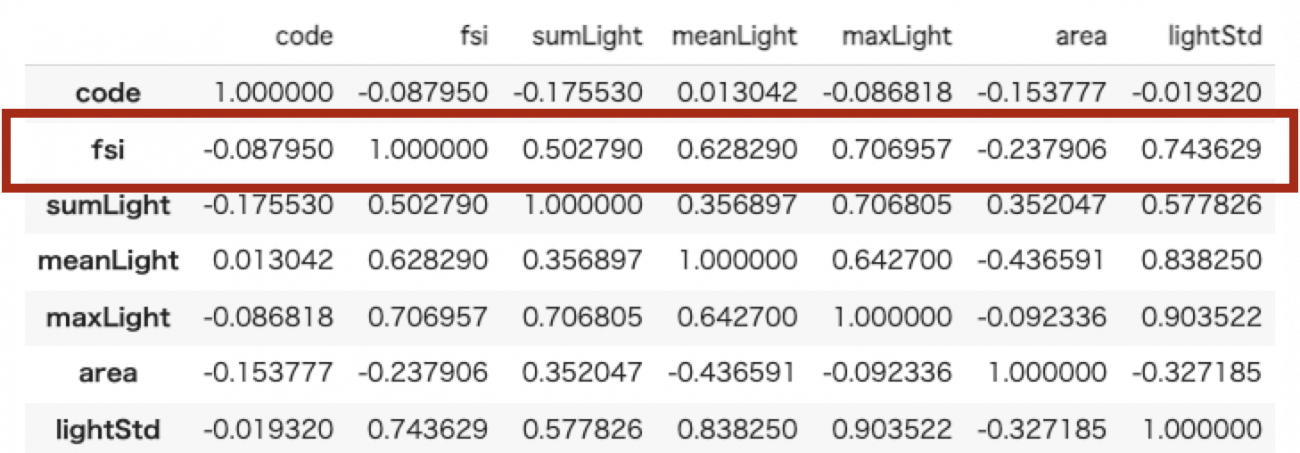
実際に相関係数を見てみます。

dataset.corr()

最大値、ばらつきは相関係数が0.7以上となっており、強い正の相関があることがわかりました。

6.3 前準備

本記事では、線形回帰モデルとランダムフォレストを適用してみます。
準備として、トレーニング用のデータとテスト用のデータでデータセットを分けます。

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 特徴量とターゲットを分割
X = dataset.drop(columns=['code', 'fsi']).astype('float64')
y = dataset['fsi'].astype('float64')

# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

6.4.機械学習

6.4.1 線形回帰モデル

まずは線形回帰モデルでクロスバリデーションを実行します。

# 線形回帰 クロスバリデーション
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

lr_model = LinearRegression()
scores = cross_val_score(lr_model, X, y, scoring='r2')

print('Cross-Validation scores: {}'.format(scores))
print('Average score: {}'.format(np.mean(scores)))

結果は以下でした。

Cross-Validation scores: [0.16447116 0.32841159 0.46352527 0.64649012 0.33741262]
Average score: 0.3880621504778688

6.4.2 ランダムフォレスト

次にランダムフォレストでクロスバリデーションを実行します。

# ランダムフォレスト クロスバリデーション
forest_model = RandomForestRegressor(random_state=42)
scores = cross_val_score(forest_model, X, y, scoring='r2')

print('Cross-Validation scores: {}'.format(scores))
print('Average score: {}'.format(np.mean(scores)))

結果は以下でした。線形回帰に比べると良い結果となりました。

Cross-Validation scores: [0.08043503 0.46811478 0.53610781 0.67483953 0.32141417]
Average score: 0.41618226129843877

7.考察

6.4項の結果から、線形回帰モデルもランダムフォレストもR2スコアが0.5未満と、正直微妙な結果となりました。とはいえ、どの特徴量が予測に効いているか考察をしてみます。

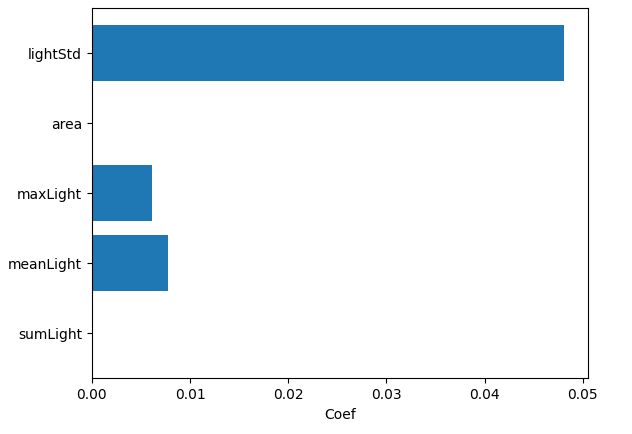
線形回帰モデルでどの特徴量が予測に寄与したか、各特徴量の係数をみてみます。

def plot_feature_coef(model, dataset):
  n_features = dataset.shape[1]
  plt.barh(range(n_features), model.coef_, align='center')
  plt.yticks(np.arange(n_features), dataset.columns.values)
  plt.xlabel('Coef')

plot_feature_coef(lr_model, X)

ばらつきが最も寄与しているようです。相関係数が最も大きかったのもばらつきのため、納得の結果ですが、最大・平均に比べて5倍以上とかなり大きめです。また、面積と合計値は係数が0となっており、全く使用されていません。

次にランダムフォレストでの各特徴量の重要度をみてみます。

def plot_feature_importances_dataset(model, dataset):
  n_features = dataset.shape[1]
  plt.barh(range(n_features), model.feature_importances_, align='center')
  plt.yticks(np.arange(n_features), dataset.columns.values)
  plt.xlabel('feature importance')

plot_feature_importances_dataset(forest_model, X)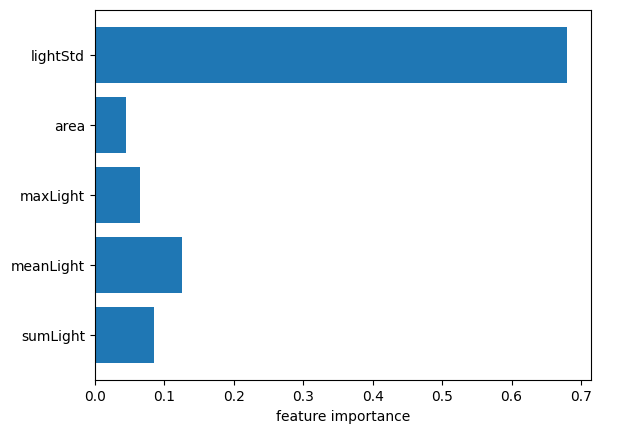

線形回帰モデル、ランダムフォレストともにばらつきが予測に最も寄与していることがわかりました。6.2項の散布図から、財政力指数とばらつきは正の相関があるため、全体的に明るい市区町村の財政力指数が高いということではなく、明るい地域と暗い地域が混在するような市区町村の財政力指数が高いことになると思われます。

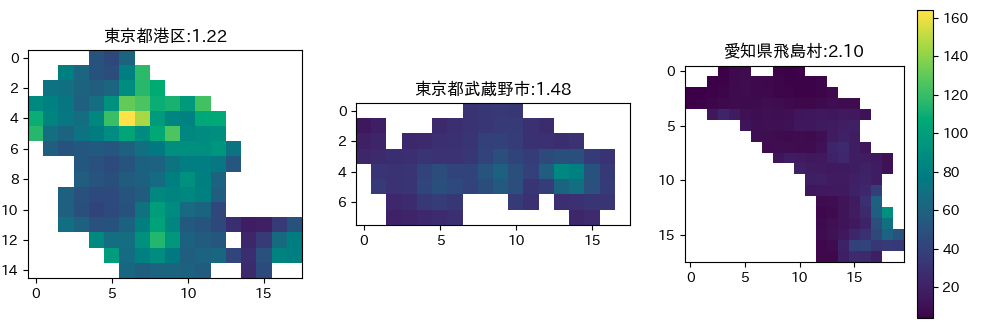
そこで、財政力指数のランキングの全国トップである愛知県飛島村、東京都で唯一TOP10入りを果たしていた東京都武蔵野市、全体的に明るそうな東京都港区(筆者の主観)の3つの市区町村について、夜間光画像を取得して表示してみます。

3つの市区町村でclip,maskした画像をGoogle Driveに保存します。

# 市区町村名と保存するファイル名を指定
# コメントアウトする市区町村を入れ替えて、3回実行してください。
target_muni = '東京都港区'
file_name = 'Tokyo_minatoku'
# target_muni = '愛知県飛島村'
# file_name = 'Aichi_tobishimamura'
# target_muni = '東京都武蔵野市'
# file_name = 'Tokyo_musashinoshi'

# 財政力指数とポリゴンデータを取得
code = data[data['市区町村名'] == target_muni]['市区町村コード'].values[0]
fsi = data[data['市区町村名'] == target_muni]['財政力指数'].values[0]
aoi = get_aoi(code, data)

#　画像のclipとmask
clipped_image = viirs.clip(aoi)
masked_image = clipped_image.updateMask(clipped_image)

# Gdriveへ保存
task = ee.batch.Export.image.toDrive(**{
    'image': masked_image,# 対象データの指定
    'description': file_name,# ファイル名の指定
    'folder':'VIIRS',# Google Drive(MyDrive)のフォルダ名
    'scale': 463.83,# 解像度の指定
    'region': aoi # 上記で指定した対象エリア
})

# 処理の実行
task.start()

画像の取得/保存の処理には少し時間がかかります。以下のコードを実行して、”False”と表示されたら、次の市区町村の画像の取得/保存を行うという手順で実行してください。(“True”と表示された場合、処理中です。)

task.active()

3つの市区町村の画像が取得できたら以下のコードでが画像を表示します。

# 東京都港区の画像を読み込み
with rasterio.open('/content/drive/My Drive/VIIRS/Tokyo_minatoku.tif') as src:
    minatoku = src.read()

# 東京都武蔵野市の画像を読み込み
with rasterio.open('/content/drive/My Drive/VIIRS/Tokyo_musashinoshi.tif') as src:
    musashinoshi = src.read()

# 愛知県飛島村の画像を読み込み
with rasterio.open('/content/drive/My Drive/VIIRS/Aichi_tobishimamura.tif') as src:
    tobishimamura = src.read()

# 画像を並べて表示するためのサブプロットを作成
fig, axes = plt.subplots(1, 3, figsize=(12, 4))

# カラーバーの最大値と最小値を設定
vmin = min(np.nanmin(minatoku[0]), np.nanmin(musashinoshi[0]), np.nanmin(tobishimamura[0]))  # 3つの配列の最小値の最小値
vmax = max(np.nanmax(minatoku[0]), np.nanmax(musashinoshi[0]), np.nanmax(tobishimamura[0]))  # 3つの配列の最大値の最大値

image_minatoku = axes[0].imshow(minatoku[0], vmin=vmin, vmax=vmax)
muni = '東京都港区'
axes[0].set_title('{}:{}'.format(muni, data[data['市区町村名'] == muni]['財政力指数'].values[0]))

image_musashinoshi = axes[1].imshow(musashinoshi[0], vmin=vmin, vmax=vmax)
muni = '東京都武蔵野市'
axes[1].set_title('{}:{}'.format(muni, data[data['市区町村名'] == muni]['財政力指数'].values[0]))

image_tobitorimura = axes[2].imshow(tobishimamura[0], vmin=vmin, vmax=vmax)
muni = '愛知県飛島村'
axes[2].set_title('{}:{}'.format(muni, data[data['市区町村名'] == muni]['財政力指数'].values[0]))

fig.colorbar(image_tobitorimura, ax=axes[2])  # カラーバーを追加

# プロットを表示
plt.show()

画像を取得することができました。どの地域も一部が明るくなっていますが、特に武蔵野市と飛島村は局所的に明るく、それ以外は暗くなっているような印象を受けます。

飛島村の財政力指数が高い理由として、南部が名古屋港の一角を占めており、貿易と物流の拠点となっていることが考えられます。つまり、それらを請け負う会社の事業所からの固定資産税が十分な収入になることが見込まれます。また、都市部に比べて人口が少ないため支出も抑えることができ、財政的には余裕が出ているのではないかと考えています。

あくまで財政力指数は「収入-支出」で表されるため、十分な収入源があり(=明るい)、なおかつ支出が抑えられる(=暗い)という両面の条件を持った地域が高くなる傾向が見て取れたと思います。
このように、単に明るさの合計や最大値が大きいだけではなく、同じ市区町村内の地域差も財政力指数に関わってくることがわかりました。

8.まとめ

夜間光のデータから特徴量を抽出し、機械学習を適用して市区町村ごとの財政力指数を予測するモデルを作成してみました。

結果は、予測精度の高いモデルは作成できませんでしたが、夜間光の最大値とばらつきとは強い正の相関があることがわかり、特にばらつきが予測に大きく寄与することがわかりました。

夜間光以外の特徴量を追加するなどすると、より良いモデルの作成ができるかもしれません。最近は単純な機械学習であれば簡単にモデルを作成できるため、みなさんも夜間光をはじめとした様々な衛星データで、機械学習に挑戦してみてはいかがでしょうか。