SAR画像で使用されるフィルターの基本と実装例、機械学習への応用【SARデータ解析者への道】
SAR (合成開口レーダー)について、使用されるフィルターの実装と適用例を紹介します。

はじめに
本記事では、SAR (合成開口レーダー)について、使用されるフィルターの実装と適用例を紹介します。さらに、フィルター選択の限界をどのように乗り越えるのかについても記載しています。
衛星画像の初心者の方には基本となる処理となりますので、ぜひ押さえていただきたい内容です。処理前後がわかりやすいように比較画像も用意しております。
また、今さらフィルター処理?って思っている方は、機械学習へ発展しているのかの先進的な軌跡についても意識してみてください。
フィルター処理の観点から考える、CNNやTransformer の機械学習による応用の理解にも繋がれば幸いです。
フィルター処理とは
SAR衛星画像は、光学画像と比較して、判読に慣れていない方にとって何が映っているのかわかりにくい画像です。そのため、何かしらの処理による情報の抽出が必要になります。
SAR(合成開口レーダー)の信号強度の画像を画像データとして扱うことで画像処理による情報の整理が可能になります。その画像処理でのデータ加工の手法の1つがフィルター処理になります。では、画像処理によるフィルター処理とはどのような処理なのでしょうか
画像処理においてのフィルター処理とは、画像を空間領域または周波数領域である範囲において演算を適用し、解析対象の成分や構造を強調しつつ不要な成分(ノイズや特定の周波数帯)を抑制する操作のことです。この時の演算は、統計処理やカーネルと言われるあるルールによって定められた計算のことです。
まずは、演算について注目して見ます。
例えば、統計処理では平均値を用いることで周囲のピクセルの平均をピクセル値に割り当てます。すると、画像全体では数値が滑らかになるので大域的な変化を捉えやすくなります。
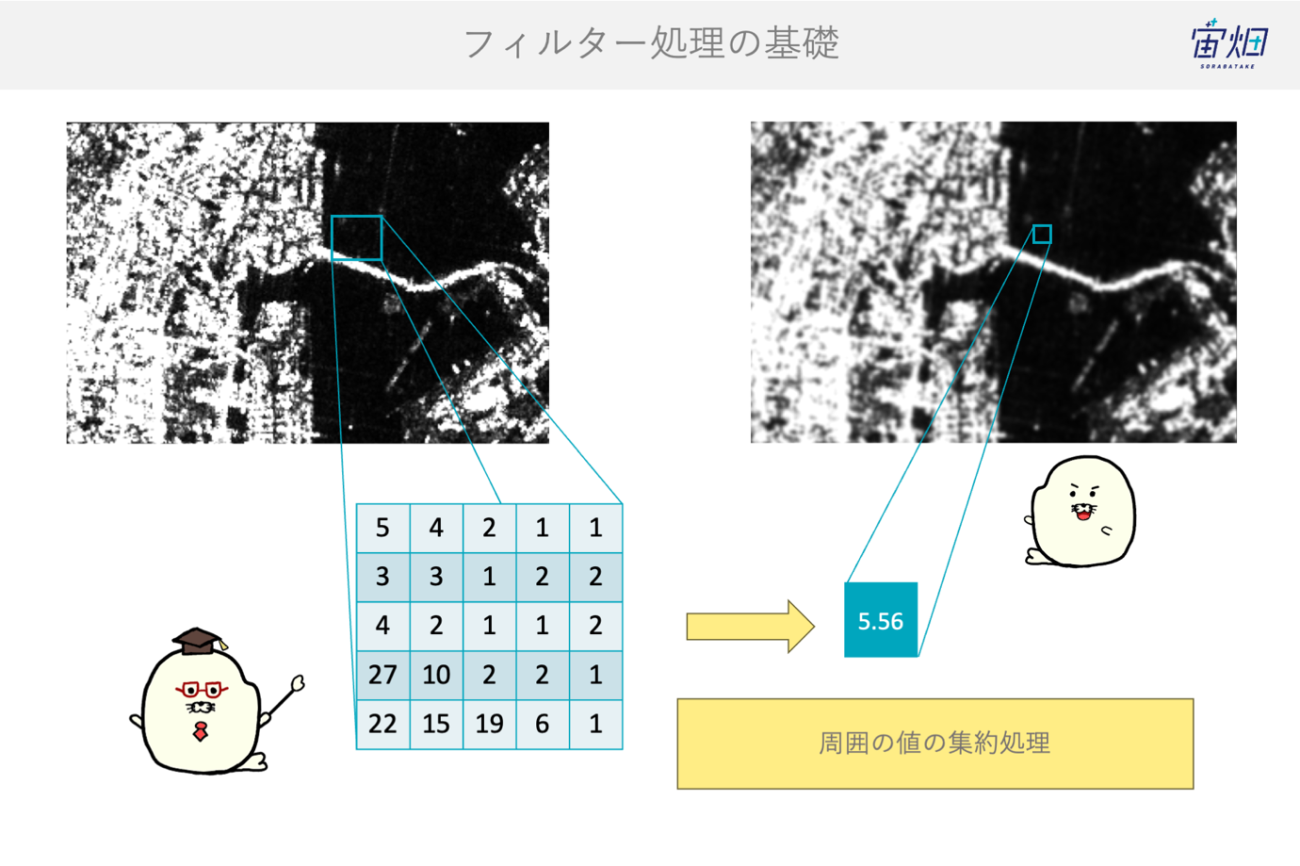
次に、処理をする範囲に注目してみます。
例えば、演算を行うピクセルを中心に周囲の7ピクセルを対象に演算を行う場合と、周囲の3ピクセルを対象に演算を行う場合では、ほとんどの場合で異なる値になります。
このように演算を行う範囲は、物理的な物体のサイズや現象に合わせた分解能や解像度に合わせてあげる必要があります。
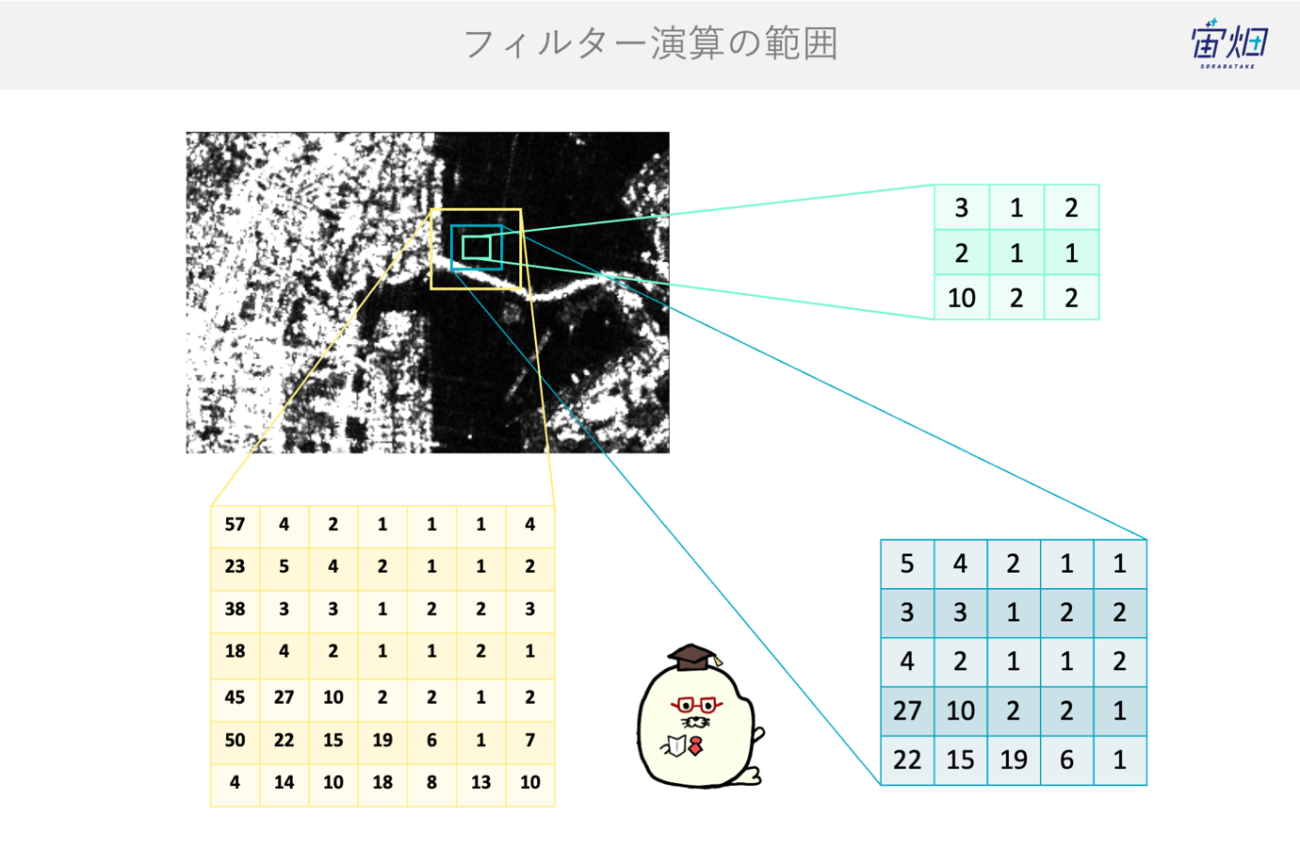
最後に、演算や範囲には沢山の種類があって実装をする時にそれぞれの条件ごとに分岐をしていては内容を理解しづらくなってしまいます。
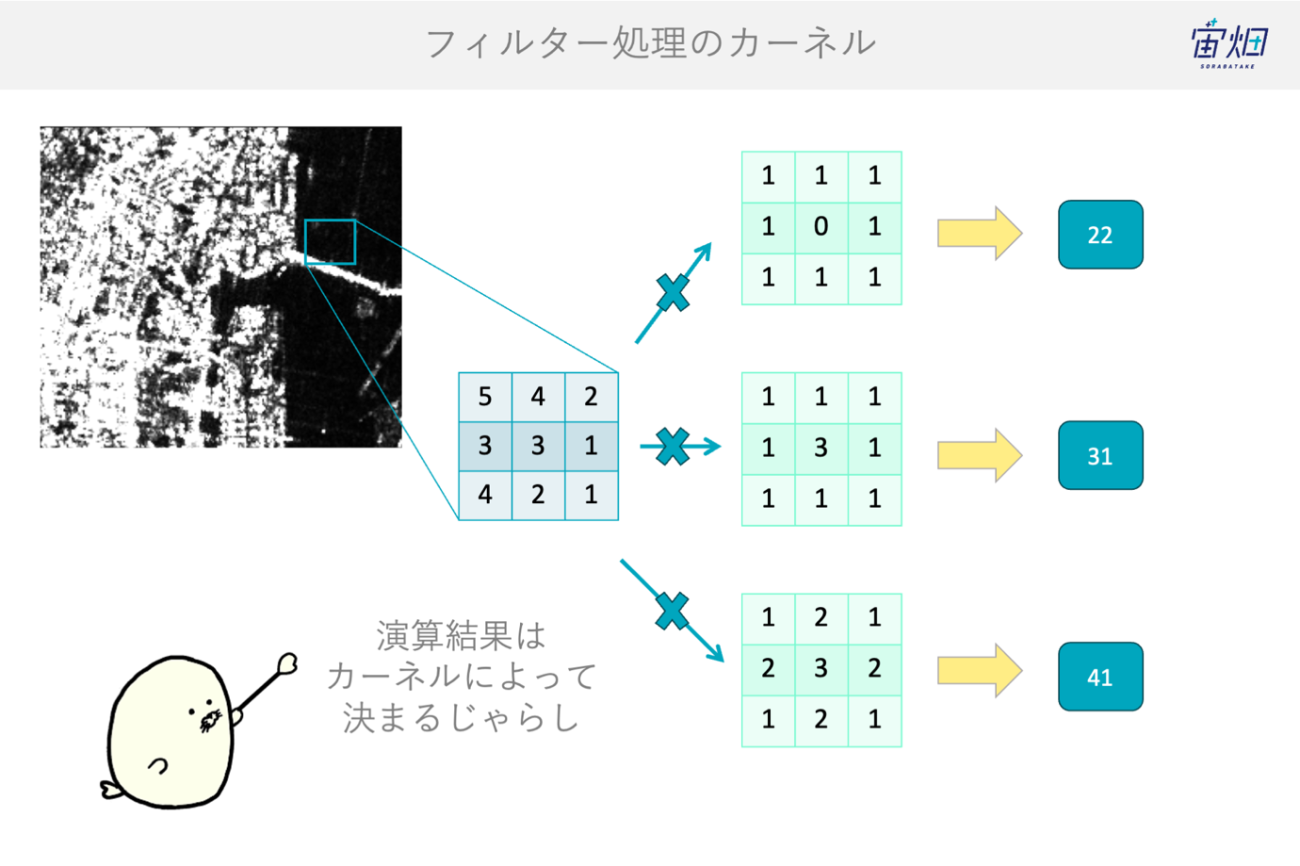
そこでこれらをわかりやすく定義するために、カーネルがあります。カーネルとは、掛け算される数字のセットのことです。次の図で示すところでは、掛け算される緑色の3×3の行列のことです。
例えば、周囲の8ピクセルは +1をして、中心の値は0を掛ける場合の合計を求める時は、図の1番上のようになります。このカーネルのサイズから 3×3 マスの範囲で、どのような演算を行うかがわかりやすいです。
そして、カーネルの値を1/3倍や2倍を適用することで出力結果をカスタマイズすることが可能です。
また、画像処理では並列演算が可能なデバイス(GPU)や画像処理ライブラリはカーネルのような同一の処理を定義してある方が、都合が良く管理しやすいです。カーネルの概念は、高速化のための工夫でもあります。

衛星画像にフィルター処理を適用する意味としては、観測する衛星のハード機器(固有の雑音やセンサー差)による変化して欲しくない変化を、解析に適した統一データに変えてくれる点にあります。
SAR衛星画像には、SARのスペックル(干渉ノイズ)、アンビギュイティなどのレーダー特有のノイズによらず、時系列変化や異なるセンサーでも解析したいからです。ソフトウェアによる自動化を実施するためにもより安定的なサービスを提供しやすくなるからです。
SAR衛星画像のノイズについては、こちらで紹介しております。
SAR画像を解析する際に理解しておきたい基礎処理【SARデータ解析者への道】
メリットは以下です。
1.ノイズ比率(本来の信号が含まれている割合)の向上により画像が「綺麗」になります。また、エッジを強化をする事で対象物(道路・海岸線・農地境界など)を抽出したい情報を選択的に強調できます。
2.近い画素(周囲の情報)を加味でき、SAR専用のLee/Refined Leeのような手法で意味のある情報(テクスチャ)は保持しつつノイズだけを抑制できます。
3.センサー間でのどうしても合わせにくいような分解能の基準が揃い、その後の処理(時空間比較や機械学習の特徴抽出)が安定します。
一方でデメリットもあります。
1.分解能の低下です。画素サイズという意味の解像度は維持できますが、本来の分解能(再現力)が低下します。特に衛星画像では重要な位置精度やエッジの強さが失われてしまいます。
2.特殊値の扱いです。衛星画像では、たまにある欠損値や異常値の補間は視覚的には改善しますが、観測対象物の本当の反射値の分布を歪めるリスクがあります。
3.悪いフィルター処理では後段の分類・回帰に誤差を招きます。不適切なカーネルは人工的なノイズを誘発し、特にSARではノイズの物理性質を無視すると良くない問題が生じやすいです。
実務上は、目的に合わせてカーネルと種類と範囲を決めます。そして、解析結果や現地データとの比較で最善のものを選んで行く流れになります。
SARフィルターの種類
では、SAR衛星画像に活用するフィルター処理について見ていきましょう。種類をざっくりと分類すると以下のようになっています。
| フィルターの分類 | 特性 | 例 |
|---|---|---|
| 統計フィルター | ・空間的に統計値をカーネルで演算に使用する基本的なフィルター ・高速に計算することが可能 |
・ガウシアンフィルター ・最大値フィルター ・中央値フィルター ・ 平均値フィルター |
| 周波数フィルター | ・周波数空間においてカーネルを演算する ・繰り返しの縞を修正やアンテナパターンの適用に有効 |
・ノッチフィルター ・ローパスフィルター ・ラプラシアンフィルター |
| SAR専用フィルター | スペックルノイズやサイドローブの原理に基づくノイズ除去のフィルター処理 | ・Leeフィルター ・Boxcarフィルター ・Frostフィルター |
| 特殊フィルター | 位相の操作や位相を強調させる処理 | ・ゴールドシュタインフィルター ・アングルコレクション |
サイドローブのノイズについてはこちらで登場しています。
衛星データのアノテーション方法~QGISでのポリゴン作成と利用する際の注意点~
まずは、統計フィルターです。SAR画像でも一般的な画像処理と同じフィルターも有効に働きます。最大や平均だけではなく、局所的な統計量(正規分布)で補正をするガウシアンフィルターもあります。
続いて、周波数フィルターです。FFTをした後のフーリエ空間で演算を行う事で周期的な補正や情報を処理に与えることが可能です。
次に、SAR専用フィルターです。合成開口レーダーは、第1弾でご紹介したようにインパルス応答によって検知を行います。その結果、スペックルノイズ(レーダーの干渉ノイズ)は、乗法ノイズと言われる掛け算のスケールでノイズが発生します。これは一般的な熱ノイズのような足し算の加法ノイズよりも大きな値で出現します。この原理に基づいた統計変化を捉えて、逆手に取ることで補正するフィルターなのでSAR専用フィルターです。
参考記事
レーダーの基礎から学ぶSAR(合成開口レーダー)の原理と奇跡【SARデータ解析者への道】
最後に、特殊なフィルターをご紹介します。今回はSAR衛星の強度画像に注目していましたが、位相に対しても適用するフィルターも存在します。合成開口処理の途中や干渉解析時の位相に対して、目的の位相に補正したり、ノイズを除去したりすることができます。
ここまでフィルター処理をご紹介したがフィルター処理にも限界があります。フィルター処理はあくまでノイズを弱めたり、対象を強調したりするだけです。闇雲に処理回数を繰り返すだけでは衛星画像にはないものを生成することがあり注意が必要です。
フィルターの実装と比較
では、実際にPythonでの実装と処理した画像の変化を比較してみて直感的な理解を深めていきましょう。
サンプルデータとしては、ESA Copernicus の Sentinel-1 というCバンドのSAR衛星のデータを使用します。データは下記に格納している VV偏波のデータを使用します。
https://github.com/syu-tan/sar-color-python-article/tree/main/data
処理の流れとしては、フィルター処理の関数を定義します。その後に、フィルター処理をして全体画像で比較をします。そして、詳細画像にて比較と共に差分を可視化します。
まずは、わかりやすい統計処理フィルターからいくつかご紹介します。
最大値フィルター
最大値フィルターについてです。
def max_filter_2d(img: np.ndarray, ksize: int = 5, cval: float = 0.0):
"""
2D(H,W)または3D(H,W,C)の画像に最大値フィルタを適用します。
- ksize は奇数(例: 5)
- cval: 埋め値
戻り値は入力と同じ dtype・形状(H,W)または(H,W,C)です。
"""
if ksize % 2 == 0:
raise ValueError("ksize は奇数である必要があります。")
if img.ndim not in (2, 3):
raise ValueError("img は2D(H,W)または3D(H,W,C)である必要があります。")
pad = ksize // 2
orig_dtype = img.dtype
if img.ndim == 2:
pad_width = ((pad, pad), (pad, pad))
padded = np.pad(img, pad_width, constant_values=cval)
win = sliding_window_view(padded, (ksize, ksize)) # (H, W, k, k)
out = win.max(axis=(-2, -1))
return out.astype(orig_dtype)
else: # (H,W,C)
H, W, C = img.shape
out = np.empty_like(img)
for c in range(C):
channel = img[..., c]
pad_width = ((pad, pad), (pad, pad))
padded = np.pad(channel, pad_width, constant_values=cval)
win = sliding_window_view(padded, (ksize, ksize)) # (H, W, k, k)
out[..., c] = win.max(axis=(-2, -1))
return out.astype(orig_dtype)周囲のピクセルに対して、カーネルのサイズでスライディングウィンドウ処理をして最大値を取得します。では、可視化します。
img_vv_max_filtered = max_filter_2d(img_vv, ksize=3)
plt.figure(figsize=(16, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 2, 1)
plt.imshow(img_vv, cmap='gray', vmin=0, vmax=1)
plt.title("Input Image (VV)")
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.subplot(1, 2, 2)
plt.imshow(img_vv_max_filtered, cmap='gray', vmin=0, vmax=1)
plt.title("Max Filtered Output (VV) with 5x5 kernel")
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_max_filtered.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();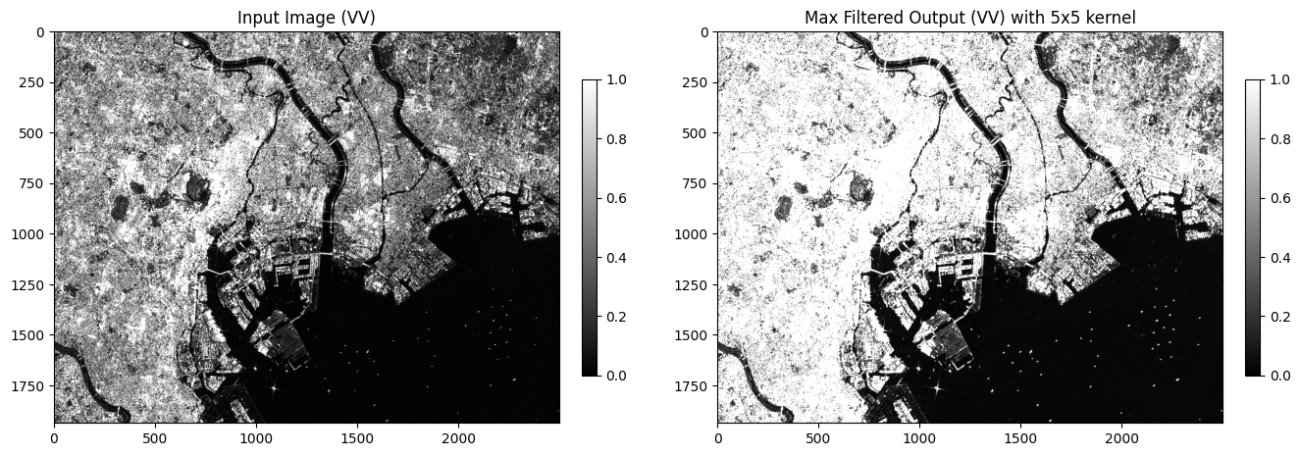
全体的に明るくなったのが分かるのではないでしょうか。
詳細部分とフィルター処理の前後の比較をしてみます。
# Patch vizualization
img_vv_max_filtered_patch = img_vv_max_filtered[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_patch = img_vv[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_diff_patch = img_vv_max_filtered_patch - img_vv_patch
plt.figure(figsize=(18, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 3, 1)
plt.title('Original VV Patch')
plt.imshow(img_vv_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 2)
plt.title('Max Filtered VV Patch')
plt.imshow(img_vv_max_filtered_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 3)
plt.title('Difference (Filtered - Original)')
plt.imshow(img_vv_diff_patch, vmin=-0.3, vmax=0.3, cmap='bwr') # 差分は-0.3〜0.3で表示
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_max_filtered_patch.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();
Credit : Contains modified Copernicus Sentinel data 2025
差分画像では、値が大きく変化した場合は、赤色。値が小さく変化した場合は、青色に変化します。最大値フィルターでは、大きい値を選択するため、差分の可視化では、真っ赤に表示されています。
中央値フィルター
次は、中央値フィルターです。関数は、scipy というライブラリーの関数を使用します。その後、可視化します。
from scipy.ndimage import median_filter
img_vv_median_filtered = median_filter(img_vv, size=5, mode="reflect")
plt.figure(figsize=(16, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 2, 1)
plt.title('Original VV')
plt.imshow(img_vv, vmin=0, vmax=1, cmap='gray')
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.subplot(1, 2, 2)
plt.title('Median Filtered VV (5x5)')
plt.imshow(img_vv_median_filtered, vmin=0, vmax=1, cmap='gray')
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_median_filtered.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();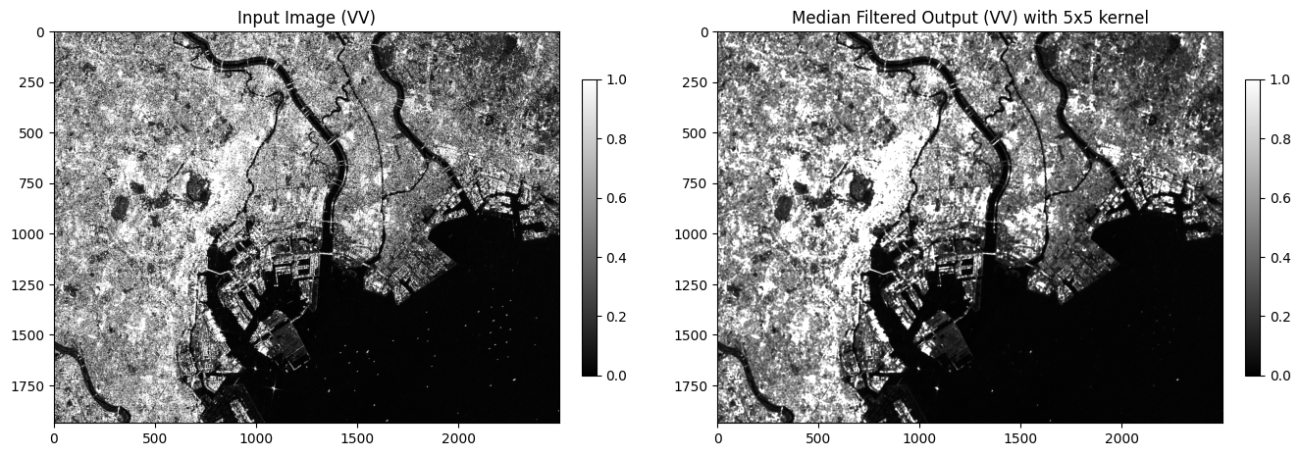
Credit : Contains modified Copernicus Sentinel data 2025
# Patch vizualization
img_vv_median_filtered_patch = img_vv_median_filtered[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_patch = img_vv[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_diff_patch = img_vv_median_filtered_patch - img_vv_patch
plt.figure(figsize=(18, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 3, 1)
plt.title('Original VV Patch')
plt.imshow(img_vv_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 2)
plt.title('Median Filtered VV Patch')
plt.imshow(img_vv_median_filtered_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 3)
plt.title('Difference (Filtered - Original)')
plt.imshow(img_vv_diff_patch, vmin=-0.3, vmax=0.3, cmap='bwr') # 差分は-0.3〜0.3で表示
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_median_filtered_patch.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();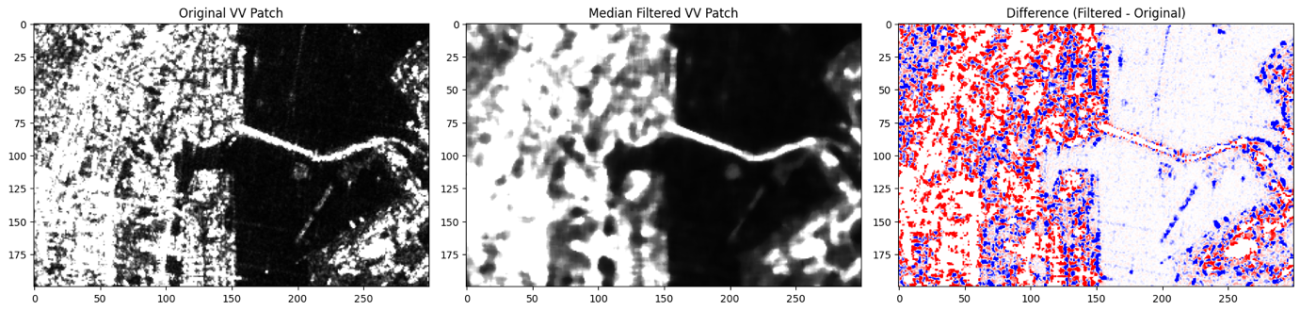
中央値フィルターでは、スペックルノイズのような局所的なピクセル値に引きずられにくいです。しかしながら、本来の値のような情報量は減りやすいです。
ガウシアンフィルター
統計フィルターの最後は、ガウシアンフィルターです。
ガウシアンフィルターは、正規分布という中心が最も値が大きく、対称な山のような分布にしたがって周囲のピクセルの値を混ぜるフィルターです。確率分布の基本で自然界でも現れることが多いです。そのため、処理後の値も直感的に自然な仕上がりになります。理論的な背景は正規分布の恩恵を多く受けます。
まずは、いくつかのガウシアンカーネルを制作します。
def gaussian_kernel1d(sigma: float, truncate: float = 3.0, *, size: int = None):
"""
1D ガウシアンカーネルを生成します(正規化済み)。
- sigma: 標準偏差
- truncate: σの何倍までで切るか(既定3σ)
- size: 明示サイズ(奇数推奨)。指定があれば truncate は無視
"""
sigma = float(sigma)
if sigma <= 0:
raise ValueError("sigma は正の値を指定してください。")
if size is None:
radius = int(truncate * sigma + 0.5)
size = 2 * radius + 1
if size % 2 == 0:
size += 1 # 奇数へ
radius = size // 2
x = np.arange(-radius, radius + 1, dtype=np.float64)
k = np.exp(-(x * x) / (2.0 * sigma * sigma))
k /= k.sum()
return k
# 代表的なカーネルをいくつか用意
GAUSS_PRESETS = {
"g3_s0.6": gaussian_kernel1d(0.6, size=3),
"g5_s1.0": gaussian_kernel1d(1.0, size=5),
"g7_s1.5": gaussian_kernel1d(1.5, size=7),
"g9_s2.0": gaussian_kernel1d(2.0, size=9),
"g11_s2.5": gaussian_kernel1d(2.5, size=11),
}そして、フィルターからレンジとアジマス方向にそれぞれ処理を適用します。
def _convolve1d_ignore_nan(arr: np.ndarray, kernel: np.ndarray, axis: int,
pad_mode: str = "reflect", constant_values: float = 0.0):
"""
1D 畳み込み(各行/列ごとに)を行い、NaNは無視(重みで割って正規化)します。
"""
if arr.ndim != 2:
raise ValueError("2次元配列を想定しています。")
if axis not in (0, 1):
raise ValueError("axis は 0(縦)または 1(横)です。")
k = kernel.astype(np.float64)
r = k.size // 2
H, W = arr.shape
out = np.empty_like(arr, dtype=np.float64)
if axis == 1: # 横方向(行ごと)
for y in range(H):
row = arr[y, :]
mask = ~np.isnan(row)
row_filled = np.where(mask, row, 0.0)
pad_kwargs = {"mode": pad_mode}
if pad_mode == "constant":
pad_kwargs["constant_values"] = constant_values
s = np.pad(row_filled, (r, r), **pad_kwargs)
m = np.pad(mask.astype(np.float64), (r, r), **pad_kwargs)
num = np.convolve(s, k, mode="valid")
den = np.convolve(m, k, mode="valid")
out_row = num / np.maximum(den, 1e-12)
out_row[den == 0.0] = np.nan
out[y, :] = out_row
return out
else: # 縦方向(列ごと)
for x in range(W):
col = arr[:, x]
mask = ~np.isnan(col)
col_filled = np.where(mask, col, 0.0)
pad_kwargs = {"mode": pad_mode}
if pad_mode == "constant":
pad_kwargs["constant_values"] = constant_values
s = np.pad(col_filled, (r, r), **pad_kwargs)
m = np.pad(mask.astype(np.float64), (r, r), **pad_kwargs)
num = np.convolve(s, k, mode="valid")
den = np.convolve(m, k, mode="valid")
out_col = num / np.maximum(den, 1e-12)
out_col[den == 0.0] = np.nan
out[:, x] = out_col
return out
def gaussian_filter_np(img: np.ndarray,
sigma: float = 1.0,
truncate: float = 3.0,
size: int = None,
kernel: np.ndarray = None,
ignore_nan: bool = True,
pad_mode: str = "reflect",
constant_values: float = 0.0):
"""
NumPyのみのガウシアンフィルター(2D)。
- sigma/size/truncate で 1D カーネルを生成(または kernel を直接渡す)
- ignore_nan=True で NaN をマスクとして無視
- pad_mode: 'reflect'|'edge'|'constant' など
"""
if img.ndim != 2:
raise ValueError("img は 2次元配列である必要があります。")
if kernel is None:
k = gaussian_kernel1d(sigma, truncate, size=size)
else:
k = np.asarray(kernel, dtype=np.float64)
if k.ndim != 1:
raise ValueError("kernel は 1次元配列を渡してください(分離畳み込み)。")
arr = img.astype(np.float64, copy=False)
if ignore_nan:
# 横 → 縦(NaN無視)
tmp = _convolve1d_ignore_nan(arr, k, axis=1, pad_mode=pad_mode, constant_values=constant_values)
out = _convolve1d_ignore_nan(tmp, k, axis=0, pad_mode=pad_mode, constant_values=constant_values)
return out
else:
# NaNを0埋め(またはそのまま)で普通に畳み込み
tmp = _convolve1d_ignore_nan(arr, k, axis=1, pad_mode=pad_mode, constant_values=constant_values)
out = _convolve1d_ignore_nan(tmp, k, axis=0, pad_mode=pad_mode, constant_values=constant_values)
return out可視化してみましょう。
img_vv_gauss_filtered = gaussian_filter_np(img_vv, kernel=k, pad_mode="reflect")
plt.figure(figsize=(16, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 2, 1)
plt.imshow(img_vv, cmap='gray', vmin=0, vmax=1)
plt.title("Input Image (VV)")
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.subplot(1, 2, 2)
plt.imshow(img_vv_gauss_filtered, cmap='gray', vmin=0, vmax=1)
plt.title("Gaussian Filtered Output (VV) with g5_s1.0 kernel")
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_gaussian_filtered.png'), bbox_inches='tight', pad_inches=0.1)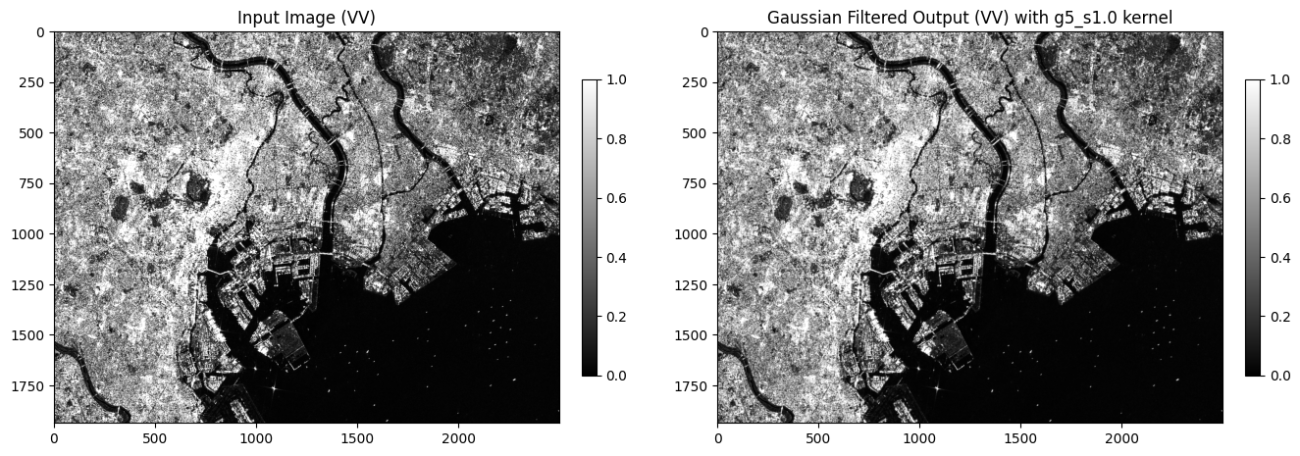
比較もしてみます。
img_vv_gauss_filtered_patch = img_vv_gauss_filtered[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_patch = img_vv[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_diff_patch = img_vv_gauss_filtered_patch - img_vv_patch
plt.figure(figsize=(18, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 3, 1)
plt.title('Original VV Patch')
plt.imshow(img_vv_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 2)
plt.title('Gaussian Filtered VV Patch')
plt.imshow(img_vv_gauss_filtered_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 3)
plt.title('Difference (Filtered - Original)')
plt.imshow(img_vv_diff_patch, vmin=-0.3, vmax=0.3, cmap='bwr') # 差分は-0.3〜0.3で表示
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_gaussian_filtered_patch.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();
周波数フィルター
さて、次は周波数フィルターをご紹介します。
主な処理の流れとしては、高速フーリエ変換(Fast Fourier Transform; FFT)を行って、周波数空間に変換します。その後に、フーリエ空間でカーネル処理をします。特定の周波数に影響を与えることで画像全体を補正します。最後に、周波数空間から時間空間に戻します。
def apply_fft_filter2d(img, H):
F = np.fft.fft2(img)
Fs = np.fft.fftshift(F)
out = np.fft.ifft2(np.fft.ifftshift(Fs * H))
return out実装としては、H がカーネルの役割です。
まずは、バターワースのローパスフィルターです。一般的なローパスフィルターは物体の外形が現れやすい低周波のみを抽出することで細かいノイズを取り除く効果があります。しかしながら、高周波も上手に残す戦略がバターワースのローパスフィルターです。適用する周波数から離れれば離れるほど、影響を減衰させるようにしています。
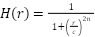
C が影響範囲で、n が影響の強さを意味します。レーダー観点では、r = c では H =12 なのでアンテナパターンの半値(パワーが半分の -3dB)に対応させることができます。実装では以下のようになります。
def butterworth_lpf(shape, cutoff=0.25, order=2):
H, W = shape
cy, cx = H//2, W//2
yy, xx = np.ogrid[:H, :W]
r = np.sqrt(((yy-cy)/H)**2 + ((xx-cx)/W)**2)
return 1.0 / (1.0 + (r/float(cutoff))**(2*order))では、適用して比較してみましょう。
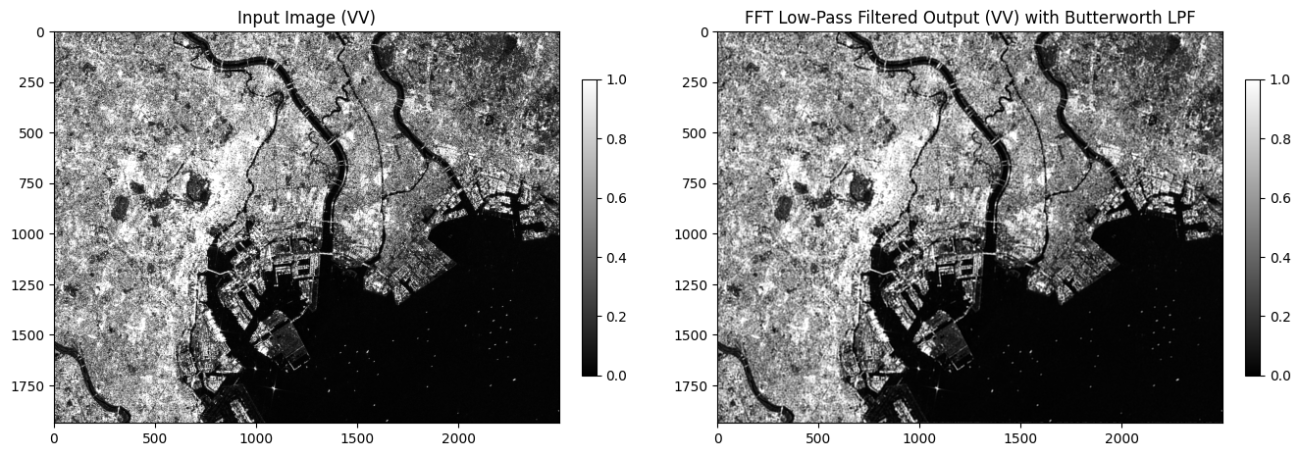
差分画像も可視化してみます。時間空間のフィルターとは少し違ったフィルター処理の効果の現れ方をしますね。

続いて、ノッチフィルターです。ノッチフィルターはある狭い周波数に対して、その影響を弱める処理です。周波数空間において、ノイズとなる領域の数値を削ぎ落とすことで特に既知の周波数ノイズの補正や縞(ストライプ・フリンジ)状のノイズを除去するには効果的です。
今回の実装では、特定の周波数領域を完全に取り除きます。
def notch_filter(shape, notches, width=3):
H, W = shape
F = np.ones(shape, np.float64)
cy, cx = H//2, W//2
for fy, fx in notches:
y = int(round(cy + fy*H))
x = int(round(cx + fx*W))
F[max(0,y-width):y+width+1, max(0,x-width):x+width+1] = 0.0
return Fでは、適用して可視化してみましょう。見た目は少しわかりにくいです。
Hn = notch_filter(img_vv.shape, notches=[(.0, 0.01), (0.0, -0.01)], width=3)
img_vv_notch = np.real(apply_fft_filter2d(img_vv, Hn))
plt.figure(figsize=(16, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 2, 1)
plt.imshow(img_vv, cmap='gray', vmin=0, vmax=1)
plt.title("Input Image (VV)")
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.subplot(1, 2, 2)
plt.imshow(img_vv_notch, cmap='gray', vmin=0, vmax=1)
plt.title("FFT Notch Filtered Output (VV)")
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_fft_notch_filtered.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();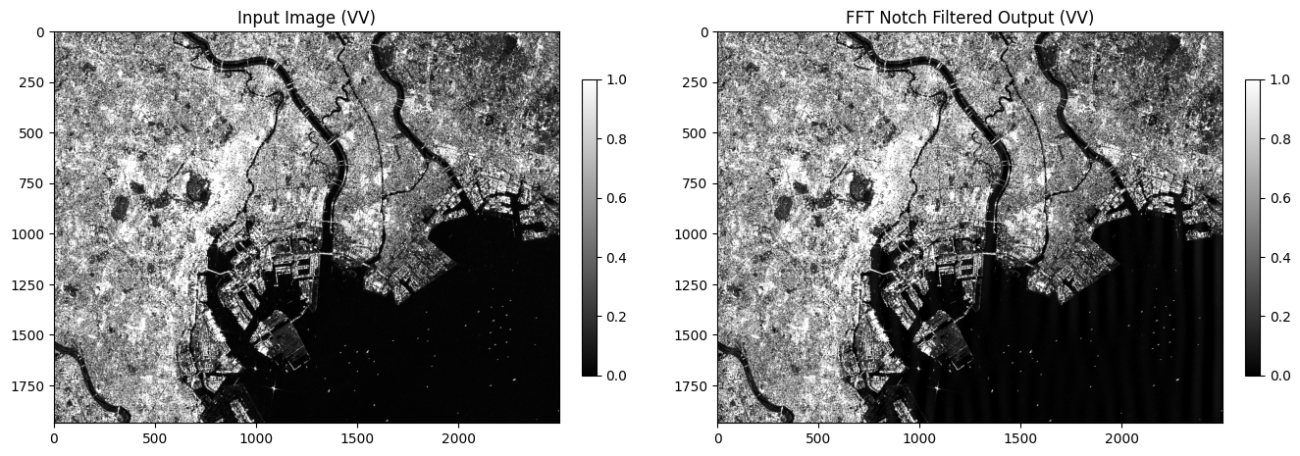
しかし、差分画像を比較すると縞状に誤差が出てきています。
img_vv_notch_patch = img_vv_notch[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_patch = img_vv[H_TOP:H_BOTTOM, W_TOP:W_BOTTOM]
img_vv_diff_patch = img_vv_notch_patch - img_vv_patch
plt.figure(figsize=(18, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 3, 1)
plt.title('Original VV Patch')
plt.imshow(img_vv_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 2)
plt.title('FFT Notch Filtered VV Patch')
plt.imshow(img_vv_notch_patch, vmin=0, vmax=1, cmap='gray')
plt.subplot(1, 3, 3)
plt.title('Difference (Filtered - Original)')
plt.imshow(img_vv_diff_patch, vmin=-0.1, vmax=0.1, cmap='bwr') # 差分は-0.1〜0.1で表示
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_fft_notch_filtered_patch.png'), bbox_inches='tight', pad_inches=0.1)
plt.show();
この縞を操作できる振る舞いを補正に使うことで、逆にデスカロッピング処理などに応用が可能です。
最後に、本命となるSAR専用フィルターの実装です。具体的な処理内容については、統計量をSARの現象に合わせてカスタマイズしているだけで、実装だけではSAR専用フィルターかどうかは分類できないでしょう。観点としてはレーダーの物理現象について考慮されているかどうかという点が重要です。
まずは、Frostフィルターについてです。Frostフィルターは変動係数(分散を平均の2乗で割った値)に damping 係数を適用することで過度なピクセル変動を抑えるような処理をしています。これはスペックルノイズのような乗法ノイズには効果的とされています。
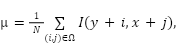
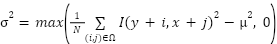
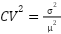
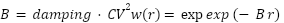
def frost_filter(img: np.ndarray,
size_y: int = 5,
size_x: int = 5,
damping: float = 2.0,
ignore_nan: bool = True,
pad_mode: str = 'reflect',
distance: str = 'euclidean',
eps: float = 1e-12):
"""
NumPyのみで実装した Frost(指数減衰)フィルター。
- img: 2次元配列(強度画像=線形スケールを想定、float推奨)
- size_y, size_x: 窓(カーネル)サイズ(奇数を推奨。偶数は内部で奇数に丸めます)
- damping: 減衰係数(SNAPの “Frost Damping Factor” に対応)
- ignore_nan: True なら NaN を無視して有効画素数で割ります
- pad_mode: np.pad のモード('reflect', 'edge', 'constant' など)
- distance: 'euclidean'(既定)または 'manhattan'。重み付け距離の定義
- eps: 0割回避用の微小量
戻り値: 入力と同じ形状の2次元配列
参考: Frostは局所統計(平均・分散)と距離に基づく指数減衰重みで
加重平均を行う代表的な SAR スペックル低減フィルター
"""
if img.ndim != 2:
raise ValueError("img は 2次元配列である必要があります。")
if size_y < 1 or size_x < 1:
raise ValueError("size_x, size_y は 1 以上にしてください。")
# 偶数は中心が曖昧になるので奇数へ丸め
if size_y % 2 == 0: size_y |= 1
if size_x % 2 == 0: size_x |= 1
H, W = img.shape
py, px = size_y // 2, size_x // 2
# 距離行列 r(中心が0)
yy, xx = np.mgrid[0:size_y, 0:size_x]
dy = yy - py
dx = xx - px
if distance == 'manhattan':
r = np.abs(dy) + np.abs(dx)
else:
r = np.sqrt(dy*dy + dx*dx)
r = r.astype(np.float64)
img = img.astype(np.float64, copy=False)
# --- 窓内平均・分散(積分画像で高速化) ---
if ignore_nan:
valid = (~np.isnan(img)).astype(np.float64)
img0 = np.where(valid, img, 0.0)
pad_img = np.pad(img0, ((py, py), (px, px)), mode=pad_mode)
pad_img2 = np.pad(img0*img0, ((py, py), (px, px)), mode=pad_mode)
pad_val = np.pad(valid, ((py, py), (px, px)), mode=pad_mode)
S = pad_img.cumsum(0).cumsum(1)
S2 = pad_img2.cumsum(0).cumsum(1)
Wv = pad_val.cumsum(0).cumsum(1)
def wnd_sum(I):
return I[size_y:, size_x:] - I[:-size_y, size_x:] - I[size_y:, :-size_x] + I[:-size_y, :-size_x]
sum1 = wnd_sum(S)
sum2 = wnd_sum(S2)
cnt = wnd_sum(Wv)
mean = sum1 / np.maximum(cnt, 1.0)
mean2 = sum2 / np.maximum(cnt, 1.0)
var = np.maximum(mean2 - mean*mean, 0.0)
B = damping * (var / np.maximum(mean*mean, eps)) # CV^2ベース
out_num = np.zeros_like(mean)
out_den = np.zeros_like(mean)
Hout, Wout = mean.shape
# 位置ごとのBに対して、各オフセットの距離rで指数重みを掛ける
for oy in range(size_y):
for ox in range(size_x):
region_img = pad_img[oy:oy+Hout, ox:ox+Wout]
region_val = pad_val[oy:oy+Hout, ox:ox+Wout]
wmap = np.exp(-B * r[oy, ox])
out_num += wmap * region_img
out_den += wmap * region_val
out = out_num / np.maximum(out_den, eps)
out[out_den == 0] = np.nan
return out
else:
pad_img = np.pad(img, ((py, py), (px, px)), mode=pad_mode)
pad_img2 = np.pad(img*img, ((py, py), (px, px)), mode=pad_mode)
S = pad_img.cumsum(0).cumsum(1)
S2 = pad_img2.cumsum(0).cumsum(1)
def wnd_sum(I):
return I[size_y:, size_x:] - I[:-size_y, size_x:] - I[size_y:, :-size_x] + I[:-size_y, :-size_x]
sum1 = wnd_sum(S)
sum2 = wnd_sum(S2)
cnt = float(size_y * size_x)
mean = sum1 / cnt
mean2 = sum2 / cnt
var = np.maximum(mean2 - mean*mean, 0.0)
B = damping * (var / np.maximum(mean*mean, eps))
out_num = np.zeros_like(mean)
out_den = np.zeros_like(mean)
Hout, Wout = mean.shape
for oy in range(size_y):
for ox in range(size_x):
region_img = pad_img[oy:oy+Hout, ox:ox+Wout]
wmap = np.exp(-B * r[oy, ox])
out_num += wmap * region_img
out_den += wmap
return out_num / np.maximum(out_den, eps)例えば、変動係数が小さく均等なデータでは、弱い抑える効果になり、変動係数が大きく不均等なデータであれば、強く抑えるような効果になります。
img_vv_frost_filtered = frost_filter(img_vv, size_y=5, size_x=5, damping=2.0, ignore_nan=True, pad_mode='reflect')
plt.figure(figsize=(16, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 2, 1)
plt.title('Original VV')
plt.imshow(img_vv, vmin=0, vmax=1, cmap='gray')
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.subplot(1, 2, 2)
plt.title('Frost Filtered VV (5x5, damping=2.0)')
plt.imshow(img_vv_frost_filtered, vmin=0, vmax=1, cmap='gray')
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_frost_filtered.png'), bbox_inches='tight', pad_inches=0.1)
plt.show(); 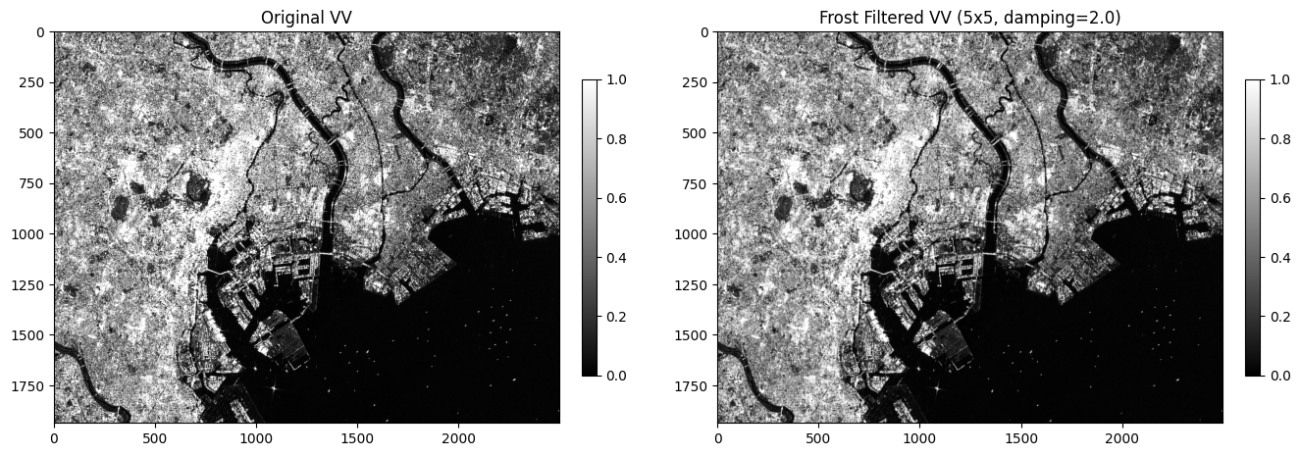
この変動係数の逆数を ENL(Equivalent Number of Looks)といい、スペックルノイズの指標として使用されたりします。この ENLがそうかするとテクスチャーが少ない滑らかな面を表していて、Frostフィルターはこの ENL が良くなる畑や水面で向いています。

続いては boxcarフィルターについてです。boxcarとは有蓋車という意味ですが、デジタル処理ではその形状から時間空間を横長の枠で平均処理をすることから移動平均を示しています。インパルス応答は、周波数空間では、sinc関数の形状になります。サイドローブがsincのように周囲に波及する場合は、そのサイズに合わせた長方形の矩形(boxcar)で抑える方が自然な仕上がりになるからです。
def boxcar_filter(img: np.ndarray, size_y: int = 5, size_x: int = 5,
ignore_nan: bool = True, pad_mode: str = 'reflect'):
"""
NumPyのみで実装したBoxcar(移動平均)フィルター。
- img: 2次元配列(強度画像を想定、float推奨)
- size_y, size_x: カーネル(窓)サイズ(奇数を推奨)
- ignore_nan: True の場合、NaN を重み0として無視し、有効画素数で割ります
- pad_mode: np.pad のモード('reflect', 'edge', 'constant' など)
戻り値: 入力と同じ形状の2次元配列
"""
if img.ndim != 2:
raise ValueError("img は 2次元配列である必要があります。")
if size_y < 1 or size_x < 1:
raise ValueError("size_x, size_y は 1 以上にしてください。")
# 偶数サイズも受け付けますが、中心定義の都合で奇数を推奨
if size_y % 2 == 0 or size_x % 2 == 0:
size_y = size_y | 1
size_x = size_x | 1
img = img.astype(np.float64, copy=False)
py, px = size_y // 2, size_x // 2
if ignore_nan:
valid = ~np.isnan(img)
img_filled = np.where(valid, img, 0.0)
pad_img = np.pad(img_filled, ((py, py), (px, px)), mode=pad_mode)
pad_val = np.pad(valid.astype(np.float64), ((py, py), (px, px)), mode=pad_mode)
# 積分画像(累積和の累積和)
S = pad_img.cumsum(axis=0).cumsum(axis=1)
W = pad_val.cumsum(axis=0).cumsum(axis=1)
# 各窓の総和と有効画素数
sum_win = S[size_y:, size_x:] - S[:-size_y, size_x:] - S[size_y:, :-size_x] + S[:-size_y, :-size_x]
cnt_win = W[size_y:, size_x:] - W[:-size_y, size_x:] - W[size_y:, :-size_x] + W[:-size_y, :-size_x]
out = sum_win / np.maximum(cnt_win, 1.0)
# 完全にNaNのみの窓だった場所はNaNに戻す
out[cnt_win == 0] = np.nan
return out
else:
pad_img = np.pad(img, ((py, py), (px, px)), mode=pad_mode)
S = pad_img.cumsum(axis=0).cumsum(axis=1)
sum_win = S[size_y:, size_x:] - S[:-size_y, size_x:] - S[size_y:, :-size_x] + S[:-size_y, :-size_x]
out = sum_win / (size_y * size_x)
return out主な振る舞いは平均フィルターと同じになります。では、可視化してみましょう。
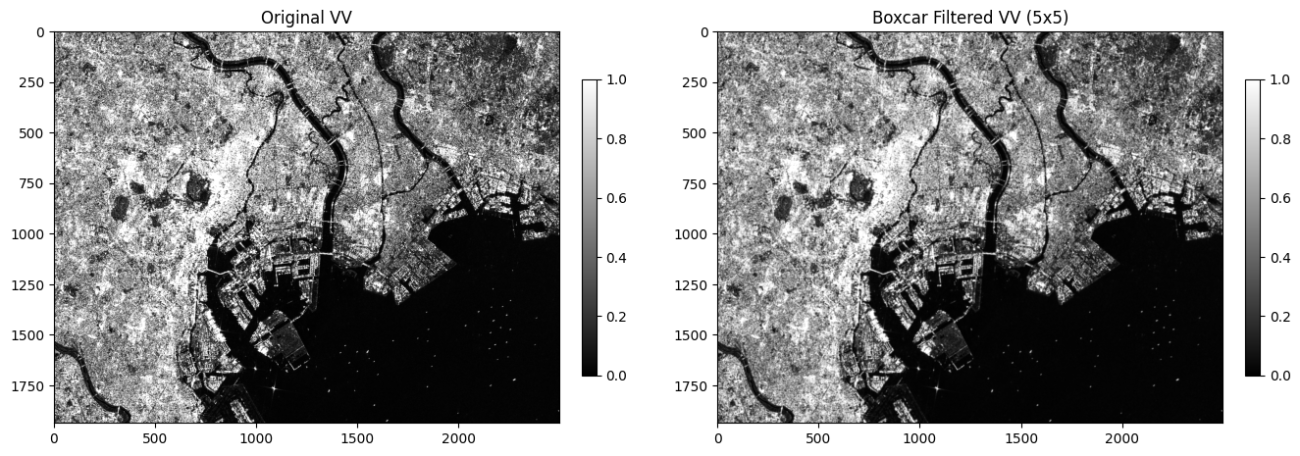
差分画像も可視化します。平均処理では、大域の特徴が抽出されるため、ローパスフィルターのような効果になります。

次は、Leeフィルターです。Leeフィルターは、ENLに基づいた乗法ノイズの抑制する処理を行います。ENLの滑らかさに合わせて強制的に乗法ノイズを抑制するようにWによる重み付けを行います。
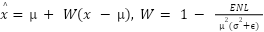
実装は以下のようになっています。
def lee_filter(img,
size_y=5, size_x=5,
enl=5.0,
input_in_db=False, # True なら dB 入力→線形に変換して処理し、dB で返す
ignore_nan=True,
pad_mode='reflect',
eps=1e-12):
"""
Lee speckle filter(クラシカル版、強度画像 2D)の NumPy 実装。
- img : 2D ndarray(線形強度 or dB)
- size_y,x : 窓サイズ(奇数推奨。偶数は内部で繰上げ)
- enl : ENL(見かけの looks 数)。S1 GRD なら 3〜7 程度が目安
- input_in_db : dB 入力を内部で線形に戻して処理 → dB で返す
- ignore_nan : NaN を無視(有効画素数で割る)
- pad_mode : 端処理モード('reflect' など)
"""
if img.ndim != 2:
raise ValueError("img は 2次元配列である必要があります。")
ky = size_y | 1
kx = size_x | 1
# 入力を線形強度へ
if input_in_db:
lin = np.power(10.0, img.astype(np.float64) / 10.0)
else:
lin = img.astype(np.float64, copy=False)
# 局所平均・分散
mean, var, cnt = _local_mean_var(lin, ky, kx, ignore_nan=ignore_nan, pad_mode=pad_mode)
# ENL からノイズ分散 σ_n^2 = μ^2 / ENL を推定(乗法スペックルの仮定)
sigma_n2 = (mean * mean) / max(enl, eps)
# Lee の重み:W = max(0, 1 - σ_n^2 / σ_l^2)
W = 1.0 - (sigma_n2 / np.maximum(var, eps))
W = np.clip(W, 0.0, 1.0)
# 推定: x_hat = μ + W * (x - μ)
x = lin
y_lin = mean + W * (x - mean)
# 欠損(窓が全NaN)の場所は NaN に
if ignore_nan:
y_lin[(cnt <= 0)] = np.nan
# 出力スケール
if input_in_db:
return 10.0 * np.log10(np.maximum(y_lin, eps))
else:
return y_linENL = 5 となるようにLeeフィルターの処理を行っていきます。
img_vv_lee_filtered = lee_filter(img_vv, size_y=5, size_x=5, enl=5.0, input_in_db=False)
plt.figure(figsize=(16, 8), dpi=100, facecolor='white', edgecolor='black')
plt.subplot(1, 2, 1)
plt.title('Original VV')
plt.imshow(img_vv, vmin=0, vmax=1, cmap='gray')
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.subplot(1, 2, 2)
plt.title('Lee Filtered VV (5x5, ENL=5.0)')
plt.imshow(img_vv_lee_filtered, vmin=0, vmax=1, cmap='gray')
plt.colorbar(fraction=0.046, pad=0.04, shrink=0.5)
plt.savefig(os.path.join(PATH_OUTPUT, 'sentinel1_vv_lee_filtered.png'), bbox_inches='tight', pad_inches=0.1)
plt.show(); 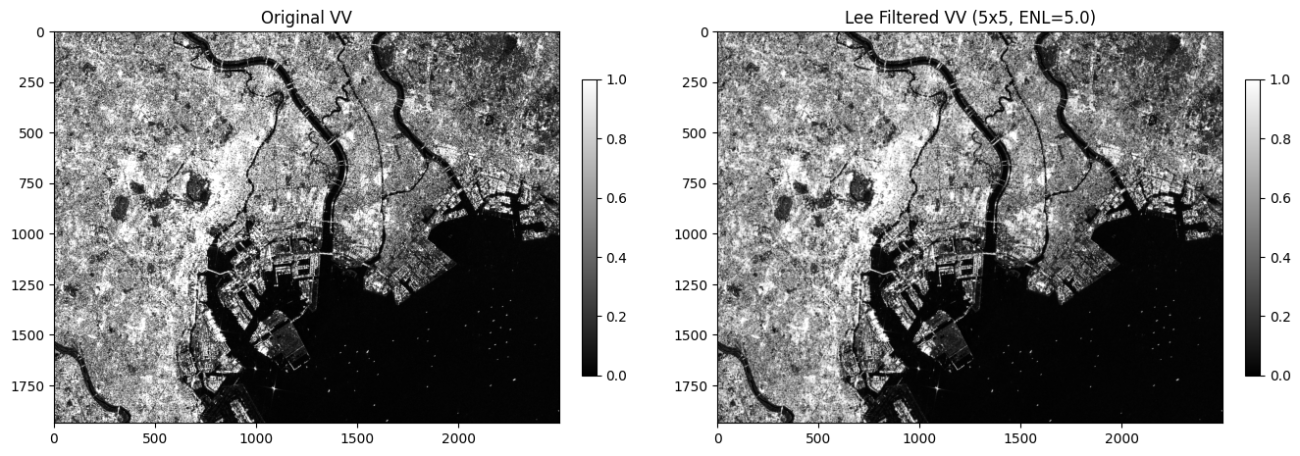
では、詳細も比較してみましょう。強い値の境界は抑制されています。

さらに、Leeフィルターはいくつかの発展系が存在します。
1つ目は、LeeSigmaフィルターです。反射面(Sigma)の値のスペックル分布に基づいた領域の統計量でLeeフィルターを算出する様に改良されています。
def _boxsum_from_padded(pad_arr, ky, kx):
S = pad_arr.cumsum(0).cumsum(1)
S = np.pad(S, ((1, 0), (1, 0)), mode='constant', constant_values=0.0)
return S[ky:, kx:] - S[:-ky, kx:] - S[ky:, :-kx] + S[:-ky, :-kx]
def _local_mean_var(img, ky, kx, ignore_nan=True, pad_mode='reflect'):
"""img と同じ (H,W) 形状で局所平均・分散・有効画素数を返します。"""
py, px = ky // 2, kx // 2
if ignore_nan:
valid = (~np.isnan(img)).astype(np.float64)
img0 = np.where(valid, img, 0.0)
pad_img = np.pad(img0, ((py, py), (px, px)), mode=pad_mode)
pad_img2 = np.pad(img0*img0, ((py, py), (px, px)), mode=pad_mode)
pad_val = np.pad(valid, ((py, py), (px, px)), mode=pad_mode)
sum1 = _boxsum_from_padded(pad_img, ky, kx)
sum2 = _boxsum_from_padded(pad_img2, ky, kx)
cnt = _boxsum_from_padded(pad_val, ky, kx)
cnt_safe = np.maximum(cnt, 1.0)
mean = sum1 / cnt_safe
mean2 = sum2 / cnt_safe
var = np.maximum(mean2 - mean*mean, 0.0)
return mean, var, cnt
else:
pad_img = np.pad(img, ((py, py), (px, px)), mode=pad_mode)
pad_img2 = np.pad(img*img, ((py, py), (px, px)), mode=pad_mode)
sum1 = _boxsum_from_padded(pad_img, ky, kx)
sum2 = _boxsum_from_padded(pad_img2, ky, kx)
cnt = float(ky * kx)
mean = sum1 / cnt
mean2 = sum2 / cnt
var = np.maximum(mean2 - mean*mean, 0.0)
return mean, var, np.full_like(mean, cnt, dtype=np.float64)
# ── Lee Sigma(Improved Sigma / MMSE) ────────────────────────────────────
# Lee et al. (2009) Table 1 に基づく A1, A2, η(looks: 1..4, sigma: 0.5..0.95)
_LEE_SIGMA_LUT = {
1: {0.5: (0.436, 1.920, 0.4057),
0.6: (0.343, 2.210, 0.4954),
0.7: (0.254, 2.582, 0.5911),
0.8: (0.168, 3.094, 0.6966),
0.9: (0.084, 3.941, 0.8191),
0.95:(0.043, 4.840, 0.8599)},
2: {0.5: (0.582, 1.584, 0.2763),
0.6: (0.501, 1.755, 0.3388),
0.7: (0.418, 1.972, 0.4062),
0.8: (0.327, 2.260, 0.4819),
0.9: (0.221, 2.744, 0.5699),
0.95:(0.152, 3.206, 0.6254)},
3: {0.5: (0.652, 1.458, 0.2222),
0.6: (0.580, 1.586, 0.2736),
0.7: (0.505, 1.751, 0.3280),
0.8: (0.419, 1.865, 0.3892),
0.9: (0.313, 2.320, 0.4624),
0.95:(0.238, 2.656, 0.5084)},
4: {0.5: (0.694, 1.385, 0.1921),
0.6: (0.630, 1.495, 0.2348),
0.7: (0.560, 1.627, 0.2825),
0.8: (0.480, 1.804, 0.3354),
0.9: (0.378, 2.094, 0.3991),
0.95:(0.302, 2.360, 0.4391)},
}
def _lut_pick(looks, sigma):
# 近傍に丸めて拾います(Lは1..4、sigmaは離散値)。厳密一致が必要ならここを変更。
Ls = sorted(_LEE_SIGMA_LUT.keys(), key=float)
sigs = sorted(next(iter(_LEE_SIGMA_LUT.values())).keys(), key=float)
L = min(Ls, key=lambda v: abs(v - looks))
s = min(sigs, key=lambda v: abs(v - sigma))
return _LEE_SIGMA_LUT[L][s]
def lee_sigma_filter(img,
win_size=9,
sigma=0.9, # Table 1 の列選択(0.5..0.95)
looks=4, # Table 1 の行選択(1..4)
tk=7, # 点ターゲット保持の 3x3 閾値(≧tkで原値保持)
input_in_db=False,
ignore_nan=True,
pad_mode='reflect',
eps=1e-12):
"""
Lee Sigma(Improved / MMSE) NumPy実装(2D強度画像)。
- img: 2D ndarray(線形強度 or dB)
- win_size: 奇数推奨(9がデフォルト)
- sigma, looks: Lee(2009) Table 1 に基づく A1, A2, η の選択
- tk: 3x3 で上位1%超の画素が tk 個以上なら原値を保持(点ターゲット保護)
"""
if img.ndim != 2:
raise ValueError("img は 2次元配列である必要があります。")
ky = kx = win_size | 1
# 入力スケール処理
if input_in_db:
lin = np.power(10.0, img.astype(np.float64) / 10.0)
else:
lin = img.astype(np.float64, copy=False)
H, W = lin.shape
# Table 1 から A1, A2, eta を取得
A1, A2, eta = _lut_pick(looks, sigma)
# η^2
eta2 = eta * eta
# まず比 r = x / μ の範囲 [A1, A2] に入る画素だけで局所統計を評価
# μ は暫定的に全画素で計算 → その μ で r を作り、範囲内だけで再計算
mean_all, var_all, _ = _local_mean_var(lin, ky, kx, ignore_nan=ignore_nan, pad_mode=pad_mode)
r = np.where(mean_all > eps, lin / mean_all, 1.0)
in_range = (r >= A1) & (r = z99).astype(np.float64)
# 3x3 の個数合計
K = _local_mean_var(over, 3, 3, ignore_nan=False, pad_mode=pad_mode)[0] * 9.0
retain = (K >= float(tk))
out_lin = np.where(retain, lin, y_lin_mmse)
# 入力が dB のときは戻す
if input_in_db:
return 10.0 * np.log10(np.maximum(out_lin, eps))
else:
return out_linこちらも同様に可視化します。
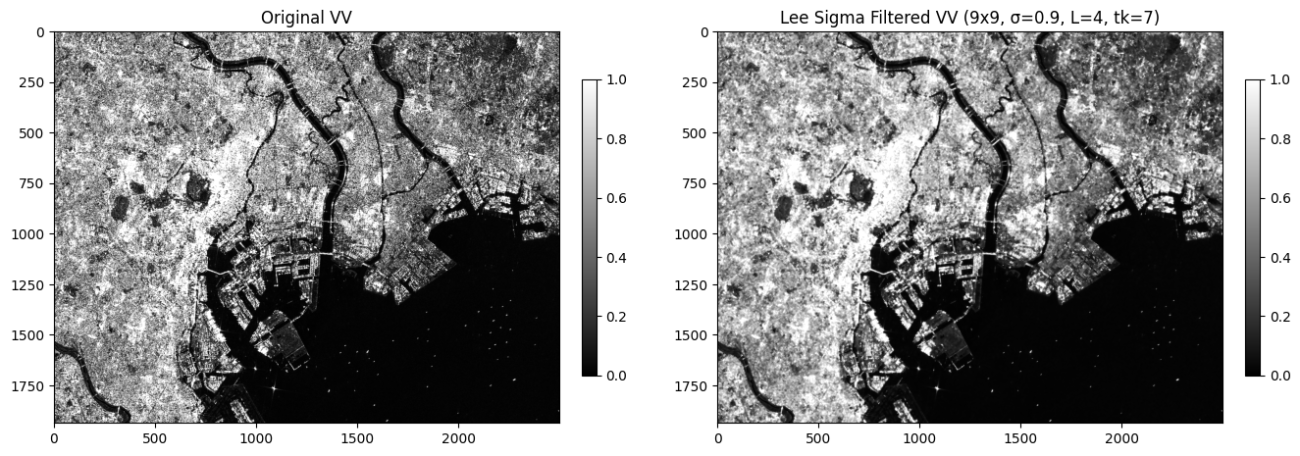
比較も見てみましょう。Leeフィルターより値が高くなりがちです。
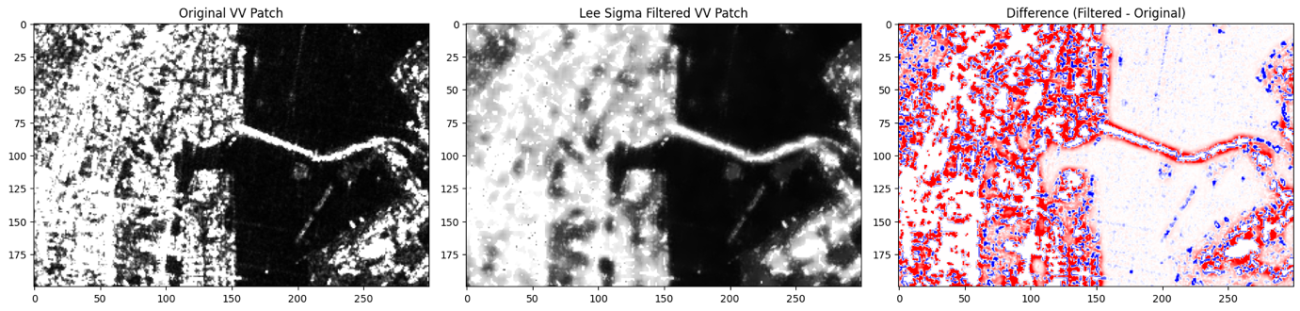
2つ目は、RefineLeeフィルターです。Leeフィルターの重みを周囲のピクセルの方向に合わせて最適化する改良です。レンジ・アジマスの時間的な倒れ込みなども方向適用することで吸収していく戦略です。
def refined_lee_filter(img: np.ndarray,
enl: float = 5.0,
win_len: int = 7, # 方向統計の線分長(奇数。典型は 7)
input_in_db: bool = False, # True なら dB 入力→線形処理→dB で返す
ignore_nan: bool = True,
pad_mode: str = 'reflect',
eps: float = 1e-12):
"""
Refined Lee speckle filter の NumPy実装(2D 強度画像用)。
アルゴリズム概要:
1) 3x3 の局所統計(平均・分散)→ ci = sqrt(var)/mean, cu = 1/sqrt(ENL)
- ci <= cu : 同質領域 → 3x3 平均を採用
- それ以外: 方向適応へ
2) 4方向(0°, 90°, 45°, 135°)の 3x3 方向勾配を計算、最小の方向を選択
3) 選択方向に沿う長さ win_len の線分窓(中心を含む)で方向平均 μ_d、分散 σ_d^2 を評価
4) ノイズ分散 σ_n^2 = μ_d^2 / ENL、Lee の重み W = max(0, 1 - σ_n^2 / σ_d^2)
出力 x̂ = μ_d + W * (x - μ_d)
引数:
img : 2D ndarray(強度=線形。dB の場合は input_in_db=True)
enl : ENL(見かけの looks)。GRD なら 3〜7 が目安
win_len : 方向窓の線分長(奇数, 推奨 7)
input_in_db: dB 入出力フラグ(内部は線形で計算)
ignore_nan : True なら NaN をマスクとして無視
pad_mode : 端処理('reflect' 推奨)
eps : 数値安定用の微小量
戻り値:
img と同形状の 2D ndarray(入力と同スケール)
"""
if img.ndim != 2:
raise ValueError("img は 2次元配列である必要があります。")
if win_len < 3 or win_len % 2 == 0:
raise ValueError("win_len は 3 以上の奇数を指定してください。")
# 入力を線形(強度)へ
if input_in_db:
x = np.power(10.0, img.astype(np.float64) / 10.0)
else:
x = img.astype(np.float64, copy=False)
H, W = x.shape
eps_enl = max(enl, eps)
# -------- 1) 3x3 局所統計 → 同質領域判定 --------
def local_mean_var_box3(a):
ky = kx = 3
py = px = 1
if ignore_nan:
valid = (~np.isnan(a)).astype(np.float64)
a0 = np.where(valid, a, 0.0)
pad_a = np.pad(a0, ((py, py), (px, px)), mode=pad_mode)
pad_a2 = np.pad(a0*a0, ((py, py), (px, px)), mode=pad_mode)
pad_v = np.pad(valid, ((py, py), (px, px)), mode=pad_mode)
S = pad_a.cumsum(0).cumsum(1); S = np.pad(S, ((1,0),(1,0)), mode='constant')
S2 = pad_a2.cumsum(0).cumsum(1); S2 = np.pad(S2, ((1,0),(1,0)), mode='constant')
V = pad_v.cumsum(0).cumsum(1); V = np.pad(V, ((1,0),(1,0)), mode='constant')
sum1 = S[ky:,kx:] - S[:-ky,kx:] - S[ky:,:-kx] + S[:-ky,:-kx]
sum2 = S2[ky:,kx:] - S2[:-ky,kx:] - S2[ky:,:-kx] + S2[:-ky,:-kx]
cnt = V[ky:,kx:] - V[:-ky,kx:] - V[ky:,:-kx] + V[:-ky,:-kx]
cnt_s = np.maximum(cnt, 1.0)
m = sum1 / cnt_s
m2 = sum2 / cnt_s
v = np.maximum(m2 - m*m, 0.0)
return m, v, cnt
else:
pad_a = np.pad(a, ((py, py), (px, px)), mode=pad_mode)
pad_a2 = np.pad(a*a, ((py, py), (px, px)), mode=pad_mode)
S = pad_a.cumsum(0).cumsum(1); S = np.pad(S, ((1,0),(1,0)), mode='constant')
S2 = pad_a2.cumsum(0).cumsum(1); S2 = np.pad(S2, ((1,0),(1,0)), mode='constant')
sum1 = S[ky:,kx:] - S[:-ky,kx:] - S[ky:,:-kx] + S[:-ky,:-kx]
sum2 = S2[ky:,kx:] - S2[:-ky,kx:] - S2[ky:,:-kx] + S2[:-ky,:-kx]
cnt = float(ky*kx)
m = sum1 / cnt
m2 = sum2 / cnt
v = np.maximum(m2 - m*m, 0.0)
return m, v, np.full_like(m, cnt, dtype=np.float64)
mean3, var3, cnt3 = local_mean_var_box3(x)
ci = np.sqrt(np.maximum(var3, 0.0)) / np.maximum(mean3, eps)
cu = 1.0 / np.sqrt(eps_enl)
homo = (ci <= cu) # 同質 → 3x3 平均
# -------- 2) 3x3 方向勾配(最小方向を選択) --------
P = np.pad(x, ((1,1),(1,1)), mode=pad_mode)
C = P[1:-1, 1:-1]
# 水平, 垂直, 対角(135° 主対角), 対角(45° 反対角)
g_h = np.abs(C - P[1:-1, 0:-2]) + np.abs(C - P[1:-1, 2:]) # 左・右
g_v = np.abs(C - P[0:-2, 1:-1]) + np.abs(C - P[2:, 1:-1]) # 上・下
g_d1 = np.abs(C - P[0:-2, 0:-2]) + np.abs(C - P[2:, 2:]) # 主対角(135°)
g_d2 = np.abs(C - P[0:-2, 2:]) + np.abs(C - P[2:, 0:-2]) # 反対角(45°)
# 順序は [水平, 垂直, 主対角, 反対角]
G = np.stack([g_h, g_v, g_d1, g_d2], axis=0)
dir_idx = np.argmin(G, axis=0) # 0..3
# -------- 3) 選択方向の 7 ピクセル線分窓で μ_d, σ_d^2 --------
L = win_len
R = L // 2
py = px = R
# パディング(線形画素/有効マスク/二乗)
if ignore_nan:
valid = (~np.isnan(x)).astype(np.float64)
x0 = np.where(valid, x, 0.0)
pad_x = np.pad(x0, ((py, py), (px, px)), mode=pad_mode)
pad_x2 = np.pad(x0*x0, ((py, py), (px, px)), mode=pad_mode)
pad_val = np.pad(valid, ((py, py), (px, px)), mode=pad_mode)
else:
pad_x = np.pad(x, ((py, py), (px, px)), mode=pad_mode)
pad_x2 = np.pad(x*x, ((py, py), (px, px)), mode=pad_mode)
pad_val = np.pad(np.ones_like(x, dtype=np.float64), ((py, py), (px, px)), mode=pad_mode)
# 方向ごとの「シフト切り出し」を合算(水平/垂直/主対角/反対角の 4 種)
def sum_shifts(pad_arr, offsets):
# pad_arr は (H+2R, W+2R)、返り値は (H, W)
H0, W0 = H, W
acc = np.zeros((H0, W0), dtype=np.float64)
for dy, dx in offsets:
acc += pad_arr[py+dy:py+dy+H0, px+dx:px+dx+W0]
return acc
offs_h = [(0, dx) for dx in range(-R, R+1)]
offs_v = [(dy, 0) for dy in range(-R, R+1)]
offs_d1 = [(k, k) for k in range(-R, R+1)] # 主対角(135°)
offs_d2 = [(k, -k) for k in range(-R, R+1)] # 反対角(45°)
sum_h = sum_shifts(pad_x, offs_h); sum2_h = sum_shifts(pad_x2, offs_h); cnt_h = sum_shifts(pad_val, offs_h)
sum_v = sum_shifts(pad_x, offs_v); sum2_v = sum_shifts(pad_x2, offs_v); cnt_v = sum_shifts(pad_val, offs_v)
sum_d1 = sum_shifts(pad_x, offs_d1); sum2_d1 = sum_shifts(pad_x2, offs_d1); cnt_d1 = sum_shifts(pad_val, offs_d1)
sum_d2 = sum_shifts(pad_x, offs_d2); sum2_d2 = sum_shifts(pad_x2, offs_d2); cnt_d2 = sum_shifts(pad_val, offs_d2)
# 有効画素で割って方向平均・分散(全NaN窓は NaN)
def mean_var(sum1, sum2, cnt):
cnt_s = np.maximum(cnt, 1.0)
m = sum1 / cnt_s
m2 = sum2 / cnt_s
v = np.maximum(m2 - m*m, 0.0)
if ignore_nan:
m[cnt <= 0] = np.nan
v[cnt <= 0] = np.nan
return m, v
mu_h, var_h = mean_var(sum_h, sum2_h, cnt_h)
mu_v, var_v = mean_var(sum_v, sum2_v, cnt_v)
mu_d1, var_d1 = mean_var(sum_d1, sum2_d1, cnt_d1)
mu_d2, var_d2 = mean_var(sum_d2, sum2_d2, cnt_d2)
# dir_idx に従って μ_d, σ_d^2 を選択
# 順序は [水平, 垂直, 主対角, 反対角] に合わせる
MU = np.stack([mu_h, mu_v, mu_d1, mu_d2], axis=0)
VAR = np.stack([var_h, var_v, var_d1, var_d2], axis=0)
# take_along_axis で (H, W) を抽出
gather_idx = dir_idx[None, :, :] # shape (1, H, W)
mu_dir = np.take_along_axis(MU, gather_idx, axis=0)[0]
var_dir = np.take_along_axis(VAR, gather_idx, axis=0)[0]
# -------- 4) Lee の MMSE 重みで推定 --------
sigma_n2 = (mu_dir * mu_dir) / eps_enl
Wt = 1.0 - sigma_n2 / np.maximum(var_dir, eps)
Wt = np.clip(Wt, 0.0, 1.0)
x_hat_dir = mu_dir + Wt * (x - mu_dir) # 方向適応
x_hat_h3 = mean3 # 同質領域は 3x3 平均
out_lin = np.where(homo, x_hat_h3, x_hat_dir)
# 全NaN窓などの扱い
if ignore_nan:
out_lin[(cnt3 <= 0)] = np.nan
# 出力スケールを戻す
if input_in_db:
return 10.0 * np.log10(np.maximum(out_lin, eps))
else:
return out_linこちらも可視化してみましょう。
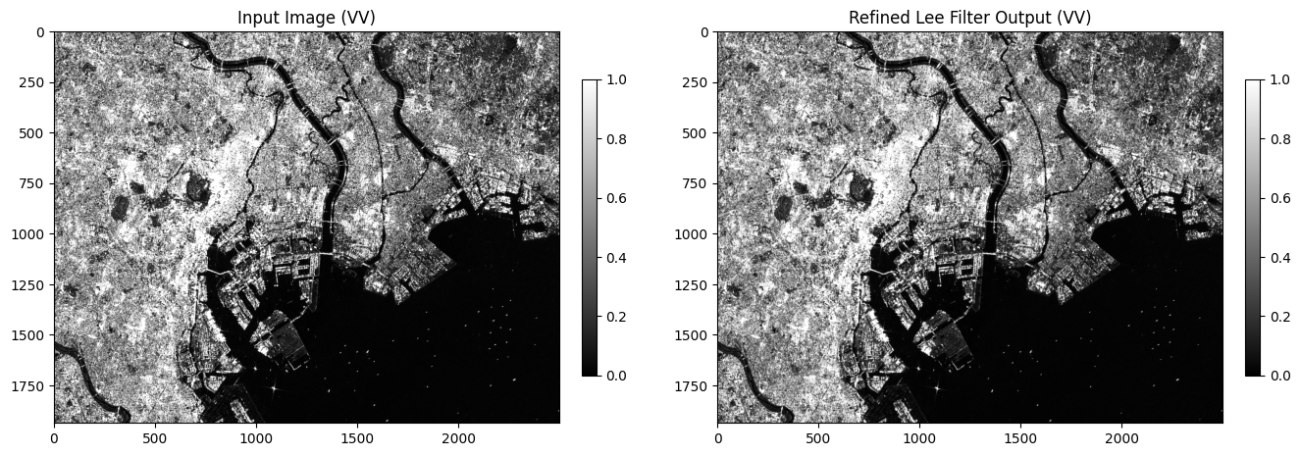
比較画像を可視化してみます。3×3枠内の処理前後では、誤差が出にくいです。

最後に、GammaMapフィルターをご紹介します。このフィルターは、変動係数ciに応じて、値をマッピングします。
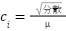
信号強度のGammaの値からマッピング処理をするため、GammaMapフィルターといいます。その後、マッピングに対応した方程式の解を再合成します。
def _boxsum_from_padded(pad_arr, ky, kx):
"""
端をパディング済みの2D配列に対して、ky×kx の全窓総和を返す。
出力形状は (H, W) になる(H,Wは元画像の形状)。
"""
S = pad_arr.cumsum(axis=0).cumsum(axis=1)
S = np.pad(S, ((1, 0), (1, 0)), mode='constant', constant_values=0.0)
# 典型的な積分画像の式
return S[ky:, kx:] - S[:-ky, kx:] - S[ky:, :-kx] + S[:-ky, :-kx]
def _local_mean_var(img, ky, kx, ignore_nan=True, pad_mode='reflect'):
"""(修正版) 画像と同じ (H,W) の局所平均・分散・有効画素数を返します。"""
py, px = ky // 2, kx // 2
if ignore_nan:
valid = (~np.isnan(img)).astype(np.float64)
img0 = np.where(valid, img, 0.0)
pad_img = np.pad(img0, ((py, py), (px, px)), mode=pad_mode)
pad_img2 = np.pad(img0*img0, ((py, py), (px, px)), mode=pad_mode)
pad_val = np.pad(valid, ((py, py), (px, px)), mode=pad_mode)
sum1 = _boxsum_from_padded(pad_img, ky, kx)
sum2 = _boxsum_from_padded(pad_img2, ky, kx)
cnt = _boxsum_from_padded(pad_val, ky, kx)
cnt_safe = np.maximum(cnt, 1.0)
mean = sum1 / cnt_safe
mean2 = sum2 / cnt_safe
var = np.maximum(mean2 - mean*mean, 0.0)
return mean, var, cnt
else:
pad_img = np.pad(img, ((py, py), (px, px)), mode=pad_mode)
pad_img2 = np.pad(img*img, ((py, py), (px, px)), mode=pad_mode)
sum1 = _boxsum_from_padded(pad_img, ky, kx)
sum2 = _boxsum_from_padded(pad_img2, ky, kx)
cnt = float(ky * kx)
mean = sum1 / cnt
mean2 = sum2 / cnt
var = np.maximum(mean2 - mean*mean, 0.0)
# 形状合わせのため cnt も配列化して返す(NaN無視しない場合は一定)
cnt_arr = np.full_like(mean, cnt, dtype=np.float64)
return mean, var, cnt_arr
def gamma_map_filter(img,
size_y=7, size_x=7,
enl=5.0,
input_in_db=False, # TrueならdB入力→線形に変換して処理、出力は入力スケールで返す
ignore_nan=True,
pad_mode='reflect',
eps=1e-12):
"""
Gamma-MAP speckle filter(Lopes 1990系)のNumPy実装(2D強度画像)。
- img: 2D ndarray(線形強度 or dB)
- size_y, size_x: 奇数推奨(偶数は内部で繰上げORにより奇数化)
- enl: ENL(見かけのlooks数)
- input_in_db: TrueならdB入力として扱い、内部で10^(x/10)→処理→dBで返す
- ignore_nan: NaNは無視(有効画素数で割る)
"""
if img.ndim != 2:
raise ValueError("imgは2次元配列である必要があります。")
ky = size_y | 1
kx = size_x | 1
# 入力スケールの扱い
if input_in_db:
lin = np.power(10.0, img.astype(np.float64) / 10.0)
else:
lin = img.astype(np.float64, copy=False)
# 局所統計
mean, var, _ = _local_mean_var(lin, ky, kx, ignore_nan=ignore_nan, pad_mode=pad_mode)
# 係数変動 ci としきい値
ci = np.sqrt(np.maximum(var, 0.0)) / np.maximum(mean, eps)
cu = 1.0 / np.sqrt(np.maximum(enl, eps))
cmax = np.sqrt(2.0) * cu
# マスク
pure = (ci cu) & (ci = cmax) # 高テクスチャ→未フィルタ
# Gamma-MAP の解
# alpha = (1 + cu^2) / (ci^2 - cu^2)
# b = alpha - (ENL + 1)
# d = mean^2 * b^2 + 4 * alpha * mean * lin * ENL
# f = (b*mean + sqrt(d)) / (2*alpha)
ci2 = ci*ci
alpha = (1.0 + cu*cu) / np.maximum(ci2 - cu*cu, eps)
b = alpha - (enl + 1.0)
d = mean*mean*b*b + 4.0*alpha*mean*lin*enl
f = (b*mean + np.sqrt(np.maximum(d, 0.0))) / np.maximum(2.0*alpha, eps)
# 合成
out_lin = np.where(pure, mean, np.where(mid, f, lin))
# 出力スケールを元に戻す
if input_in_db:
out = 10.0 * np.log10(np.maximum(out_lin, eps))
else:
out = out_lin
return out可視化してみましょう。
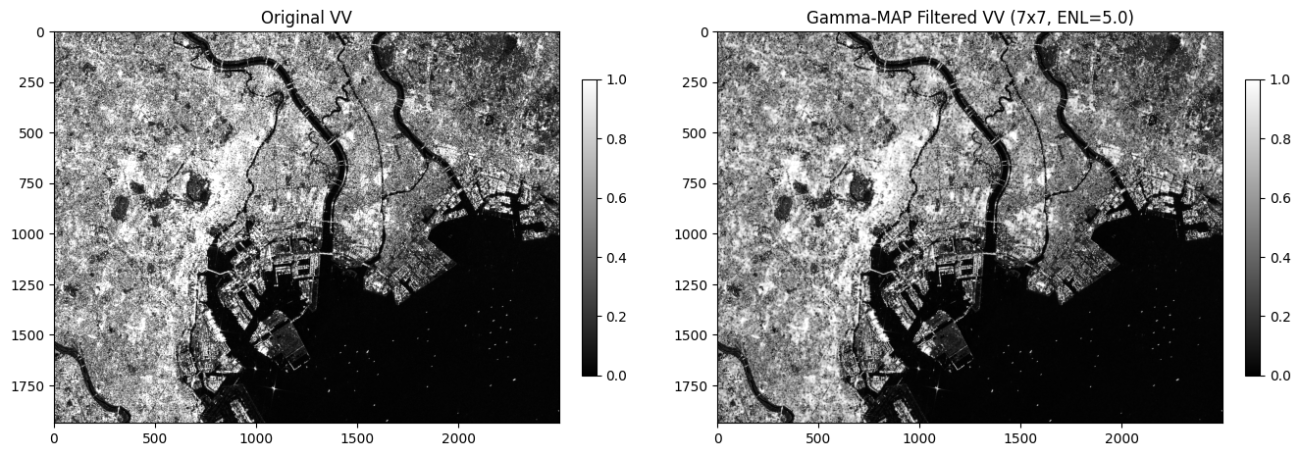
差分画像も可視化してみます。ぼかしつつも広域での物体の形は保っている様な印象です。

SAR専用フィルターについては、レーダーノイズの原理に基づいて、正規化されています。ENLをはじめとしたSAR特有の信号強度画像に合った処理をしていきましょう。
また、「結果が良ければいいよね!」だけではなく、背景理論をしっかりと考えておくことで異常な振る舞いをし難いです。そのため、汎用性の観点からも処理内容や違いを理解しておくことが大切です。
フィルター処理の限界とCNNの登場
では、ご紹介したフィルターを目的に応じてカスタムなフィルターを設計します。統計フィルター(ガウシアンや平均)、SAR専用フィルター、といった具合に、カーネルの形やスケールを調整します。必要に応じて非線形処理や複数段のパイプラインに組み合わせます。観測したい対象物の特徴に合わせて画像のスケール・多方向のフィルターを作り、しきい値や後段のルールを詰めていくことで、ある程度までは狙い通りの抽出ができます。衛星画像でも、道路や河川、建物など地物ごとに最適な組み合わせを作り込む発想はある程度までは有効です。
しかしながら、「ある程度まではなんです」。この職人芸的な最適化は次第に限界に突き当たります。観測条件や季節、センサー差による分布の揺らぎ、強度のスケールや歪みの変化に手作りが追いつかなくなるのです。フィルター数が増えるほど相互作用は複雑化し、パラメータは組合せの種類が爆発的に増加します。ある場面ではうまく機能しても、別の地域や時点では性能が崩れ、都度の再調整が必要になります。さらに、どの特徴が最終目的に有効のかという“因果”が見えにくく、設計者の勘や経験に依存しがちです。
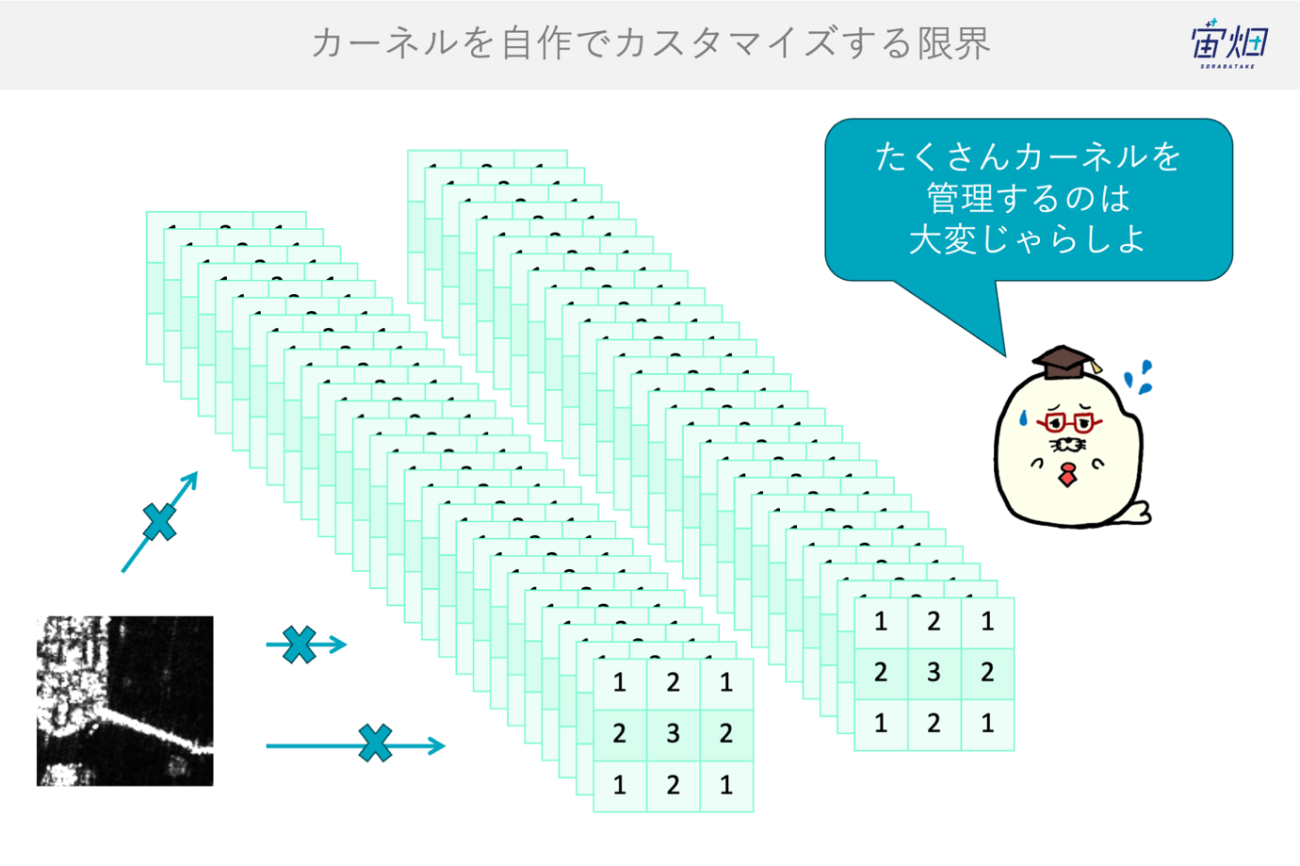
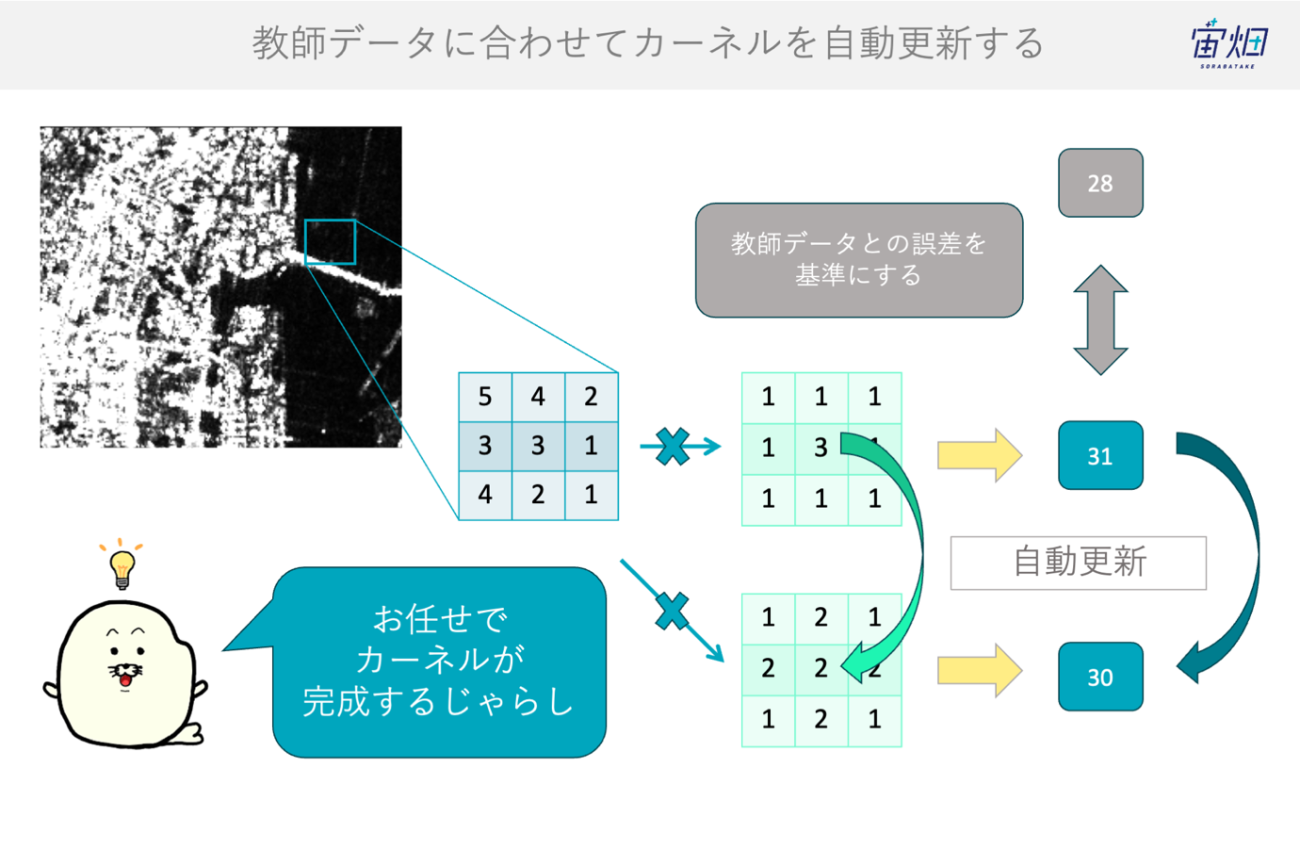
そこで発想を転換します。もし物体の場所や輪郭といった教師データ(Ground Truth; GT)があるなら、それに合わせて自動的に「フィルターそのもののカーネルを最適化」すればよいのではないか、という考えです。
すなわち、フィルター出力とGTの不一致な誤差の部分を損失関数で定義(学習目標を設定)し、カーネルを更新するという枠組みです。
この「フィルターを学習で生み出す」アプローチが畳み込みニューラルネットワーク(CNN)です。CNNでは、初段はエッジ抽出や統計フィルターに似た素朴な特徴を自動に獲得し、中間層でパーツやパターン、上位層で意味的概念へと階層的に抽象化します。
結果として、従来の手作りフィルターの長所(局所性、平行移動不変な構造)を保ちつつ、データ分布に合わせて最適化されるため、環境変動やセンサー差への適応力が高まります。要するに、物体に合わせてフィルターを「組み合わせて作る」時代から、物体の場所に合わせてフィルターを「自動で作らせる」時代に移行したのです。
フィルター処理で考えるTransformer
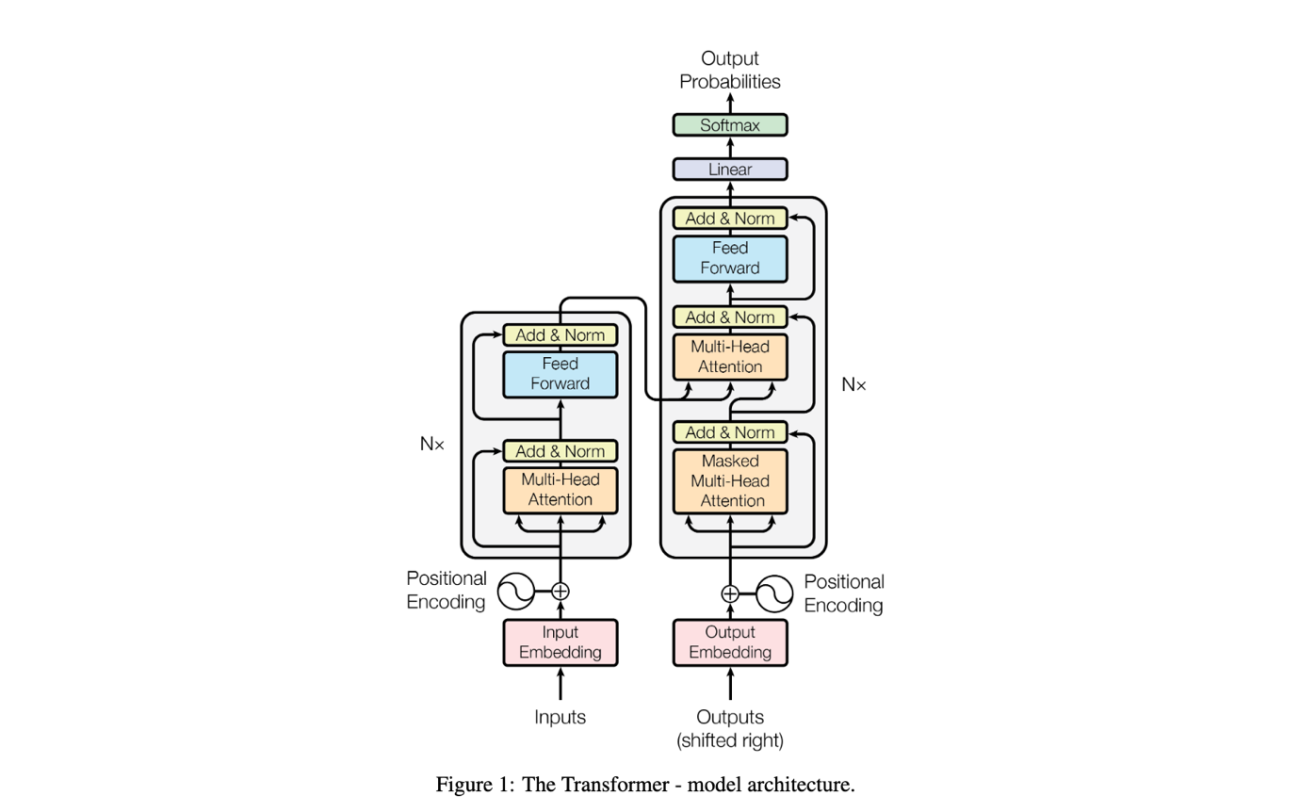
そして、まだまだ時代は進みます。フィルター処理の発想で考えると、CNNは「固定形状の多数のカーネルを学習で作る」仕組みでしたが、カーネルの大きさ(影響範囲)は段を重ねて広げるしかなく、入力画像が広域になるほど長距離の関係性を直接扱いにくいという課題が現れます。
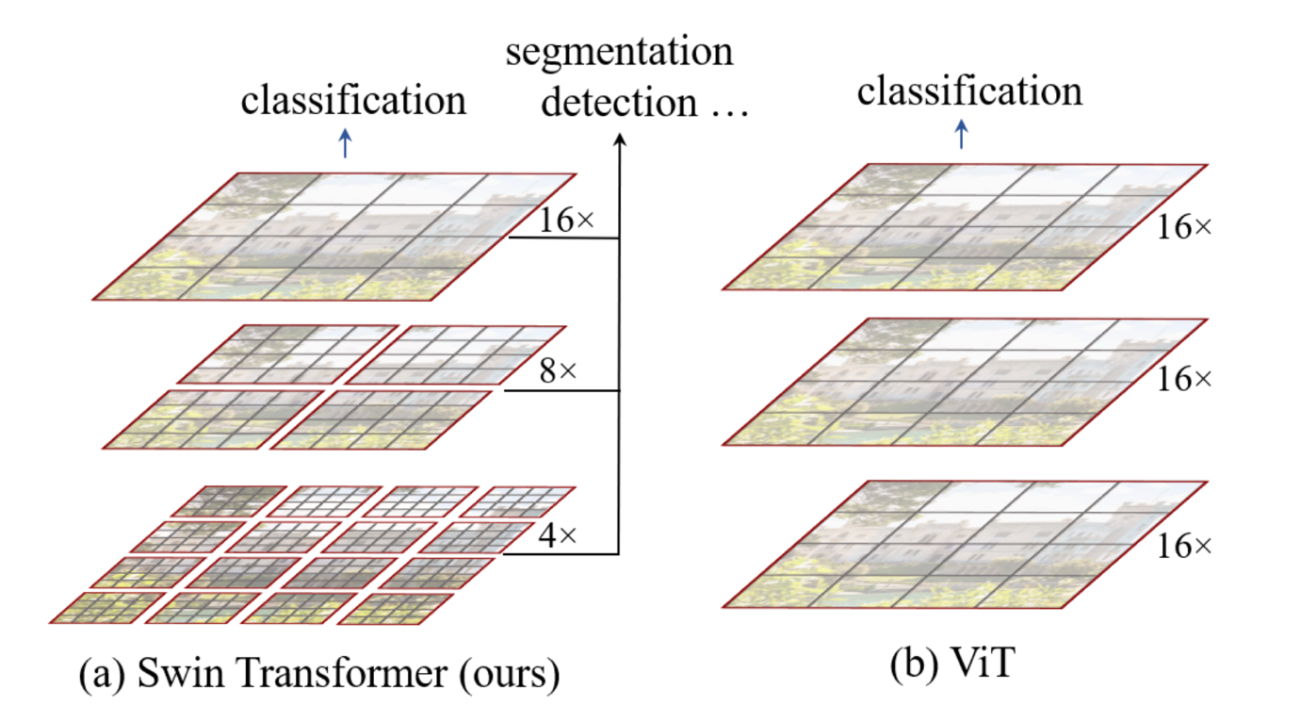
衛星画像のように数万×数万画素のシーンでは、タイル分割による境界効果や、季節・地表条件の変動に伴うコンテキストの違いが無視できず、局所カーネルの組み合わせだけでは限界が見えてまいります。
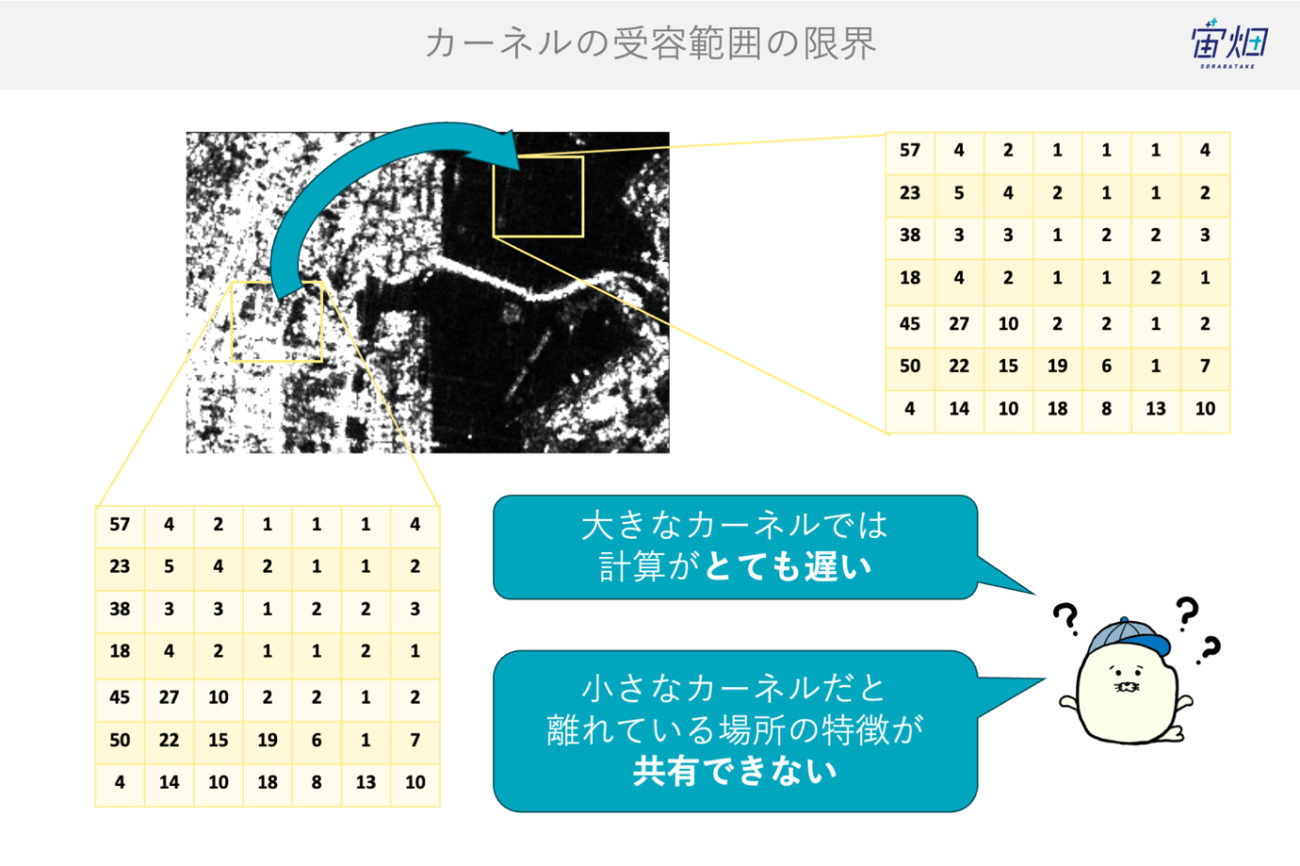
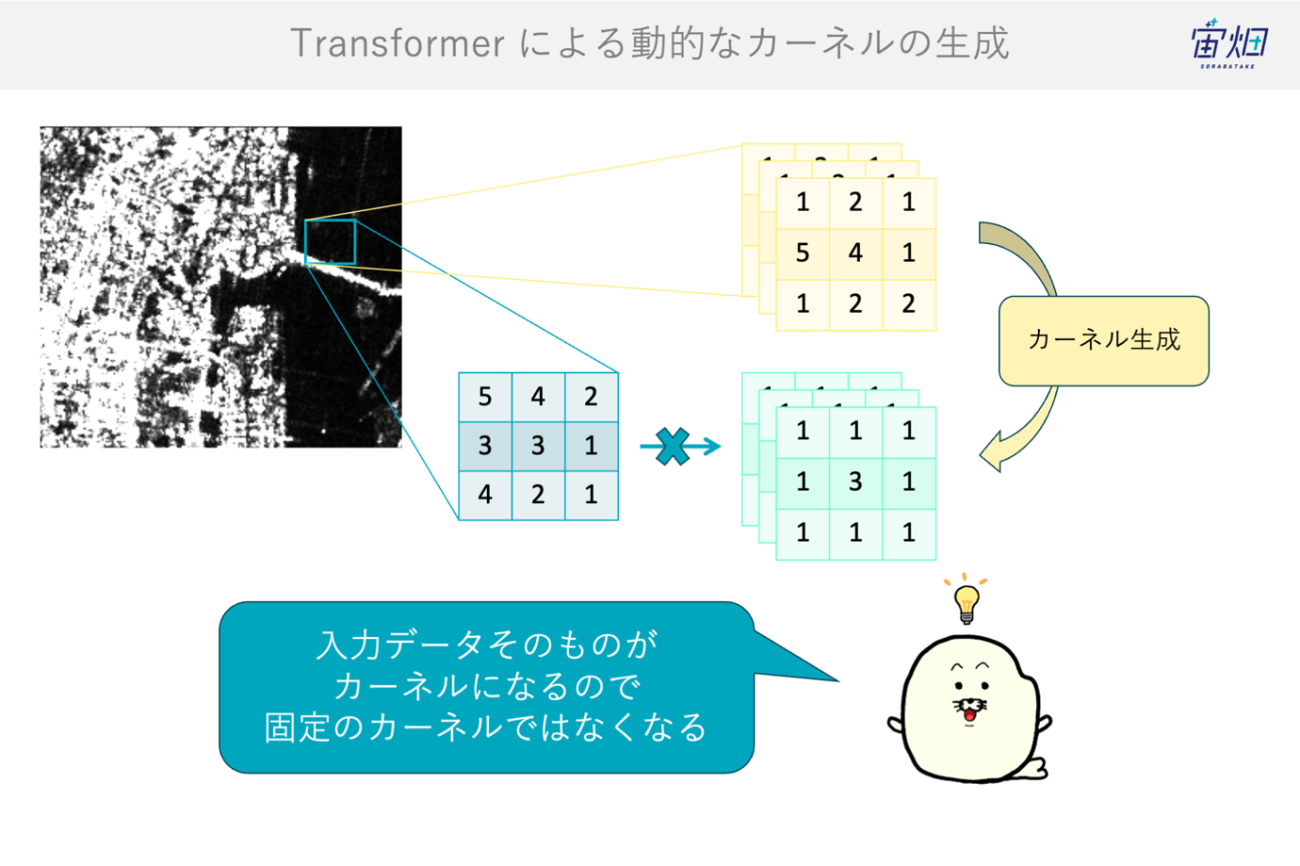
これを打破するのが Transformer です。自己注意機構(Self-Attention)は、各画素(パッチ)から算出します。入力画像のピクセル値同士の相関からその場でカーネルを生成します。言い換えれば、カーネルをデータ自身から作る“動的フィルター”です。
ある位置の特徴は、遠く離れた地点を含む全体から、関連度に応じて良いカーネルが制作される仕組みです。受容野は内容に応じて可変となり、河川と氾濫原、都市と道路網、雲と影の関係といった長距離・非局所の情報を加味する事ができます。
教師データ(GT)に適合するような動的なカーネルを最適化するため、タスクへのフィット感も高まりやすいです。また、光学衛星やSAR衛星のような融合(データフージョン)がしやすいです。いわゆる、マルチモダリティ・マルチドメイン・マルチモーダルな学習です。
しかし、良いことばかりではありません。自己注意機構は計算・メモリが画素数の二乗で増え、広域シーンでは現実的でない場合があります。また、過学習が起きやすいです。なぜなら、入力依存で変わる“動的カーネル”が不安定だからで、モデルの正規化やデータ拡張・早期打ち切り・重み減衰の制御の難易度が上がります。そして、データに依存するために「見たくない相関」(雲影やスペックルの擬似相関)に引きずられる危険性もあります。
とりわけリモートセンシングでは、放射輝度補正、SARの原理、地形(DEM)などのジオメトリによる「物理制約」が厳格です。ゆえに、AIだけに委ねず、物理に根差した制御と最適化をどうしていくかが求められます。モデルは誰でも簡単に作れる時代になったからこそ信頼できるモデルの制御が肝要です。
Transformerは「入力から自らカーネルを生成する動的なフィルター」です。広域・多様な衛星画像に強みを発揮しますが、過学習と計算量、そして物理整合の三点を丁寧に制御する――そのバランスのある設計こそがこれからのモデル戦略になる事でしょう。
まとめ
いかがだったでしょうか?SAR(合成開口レーダー)のフィルター選択とその戦略についてご紹介しました。最近でなぜ機械学習に発展しいているのかもフィルター処理の観点から考察することで有用性も捉えやすかったのではないでしょうか
引き続きSARの処理をお楽しみください!
参考文献
1.Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems 30 (2017).
2.Liu, Ze, et al. “Swin transformer: Hierarchical vision transformer using shifted windows.” Proceedings of the IEEE/CVF international conference on computer vision. 2021.
3.Lee, Jong-Sen. “Digital Image Enhancement and Noise Filtering by Use of Local Statistics.” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 2, no. 2, 1980, pp. 165–168.
4.Lee, Jong-Sen. “Digital Image Smoothing and the Sigma Filter.” Computer Vision, Graphics, and Image Processing, vol. 24, no. 2, 1983, pp. 255–269.
5.Lopes, Armand, Ridha Touzi, and Edmond Nezry. “Adaptive Speckle Filters and Scene Heterogeneity.” IEEE Transactions on Geoscience and Remote Sensing, vol. 28, no. 6, 1990, pp. 992–1000.
6.Lopes, Armand, Edmond Nezry, Ridha Touzi, and Hugues Laur. “Structure Detection and Statistical Adaptive Speckle Filtering in SAR Images.” International Journal of Remote Sensing, vol. 14, no. 9, 1993, pp. 1735–1758.
7.Lopes, Armand, Edmond Nezry, Ridha Touzi, and Hugues Laur. “Maximum A Posteriori Speckle Filtering and First Order Texture Models in SAR Images.” IGARSS ’90: Proceedings of the 1990 International Geoscience and Remote Sensing Symposium, 20–24 May 1990, IEEE, pp. 2409–2412.
8.Baraldi, Andrea, and Flavio Parmiggiani. “A Refined Gamma MAP SAR Speckle Filter with Improved Geometrical Adaptivity.” IEEE Transactions on Geoscience and Remote Sensing, vol. 33, no. 5, 1995, pp. 1245–1257.
9.Sun, Shuhan, et al. “Comparative Study on the Speckle Filters for the Very High-Resolution SAR Images.” Journal of Applied Remote Sensing, vol. 10, no. 4, 2016, 045014.
10.https://github.com/snap-stanford/snap
SARについてもっと学び、解析できるようになりたいなら
本連載「SARデータ解析者への道」の著者である安井秀輔さんが執筆した書籍『SAR衛星データ解析入門』が2026年2月27日に出版されます。本連載を通してもっとSARについて学びたい!という方にはおすすめの1冊です。


