【コード付き】地盤の沈降が分かる干渉SAR解析をTellusでやってみた
本記事では、SARの干渉解析アルゴリズムをフルスクラッチでコーディングしていきます。この記事のコードをそのまま使えば、干渉SARを誰でも実行できるようになります。
記事作成時から、Tellusからデータを検索・取得するAPIが変更になっております。該当箇所のコードについては、以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/access/traveler_api_20220310_
firstpart.html
2022年8月31日以降、Tellus OSでのデータの閲覧方法など使い方が一部変更になっております。新しいTellus OSの基本操作は以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/tellus_os/start_tellus_os.html
TellusでリリースされたPALSAR-2(JAXAが開発したALOS-2(だいち2号)に搭載されている合成開口レーダ)の標準データをみなさん活用していますでしょうか?これまで、以下の記事で、その活用方法をご紹介してきました。
【コード付き】TellusでPALSAR-2のL1.1の 画像化にチャレンジしてみた
TellusでPALSAR-2のL2.1標準処理データを使って 土地被覆の抽出にチャレンジ
本記事では、SARの干渉解析アルゴリズムをフルスクラッチでコーディングしていきます。この記事のコードをそのまま使えば、干渉SARを誰でも実行できるようになります。
一般に、干渉SARは高度な技術が必要なため、専用の商用ソフトを用いることが常識とされており、その中身についてはブラックボックスとなっています。そのため、初学者にはハードルが高く、利用者の裾野が広がらないという課題があります。本記事が、少しでもこの課題を解決するきっかけとなることを願っています。
干渉SARとは?
干渉SARとは、一言でいえば、「電波の位相差を測ることで地表面の変化を知る技術」と言えます。衛星が同じ位置から電波を放射したとき、地表面が時期によって変化していれば、それが反射波の位相のずれとして検知されるので、地表面の変化を抽出することができるのです。
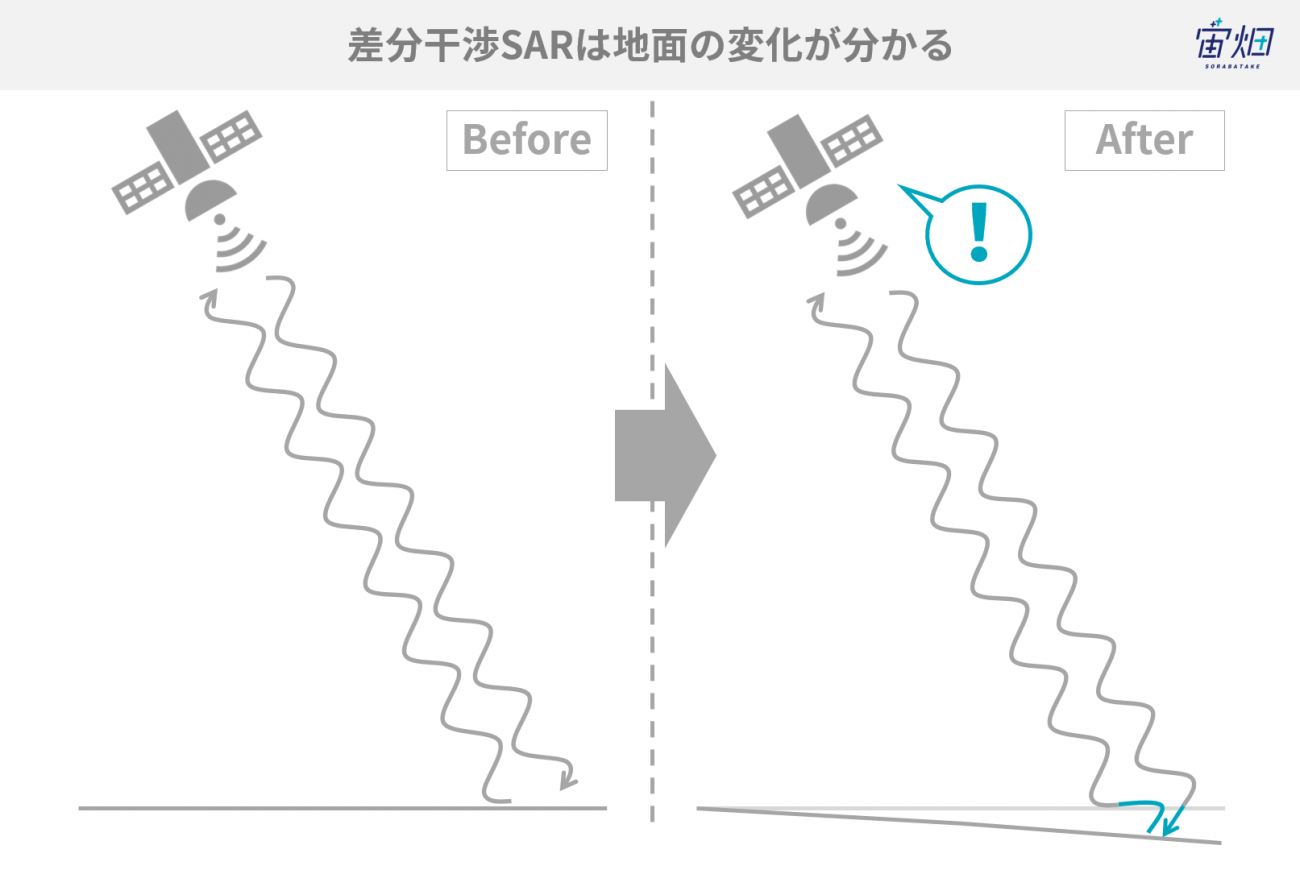
干渉SARの詳しい説明は以前に一般財団法人リモート・センシング技術センター(RESTEC)に解説していただいた記事がありますので、こちらを参照してみてください。
干渉SAR(InSAR)とは-分かること、事例、仕組み、読み解き方-
本記事では、これを実際にTellusの開発環境でプログラミングしていきたいと思います。
干渉SARの処理フローは以下の通りです。一つずつ説明していきます。

(1) 可干渉ペアを探そう
干渉SARを実践するといっても、ハードルがいくつかあります。その最初のハードルとなるのは、そもそも干渉する画像のペア(可干渉ペア)を探すことです。単純に同じ地点を写した画像なら干渉できるというわけではないのです。
干渉するための主な条件は、以下の3点です。
①同じ軌道(位置・向き)から観測したものであること
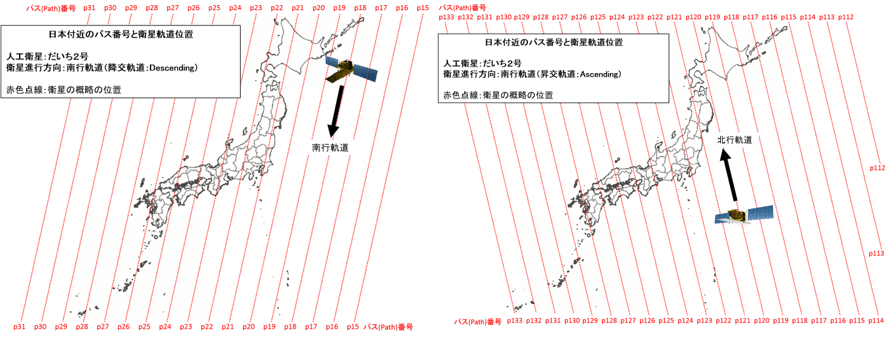
(左:北から南へ行く軌道、右:南から北へ行く軌道) Credit : 国土地理院 Source : https://insarmap.gsi.go.jp/mechanism/orbit_observation_region.html
同じ地点を写していても、その場所を写した衛星がいた場所が異なる可能性があります。違う場所から撮影していると、当然見え方が異なるので2枚の画像は干渉しません。そこで、同じ場所から撮影した画像を選ぶ必要があります。衛星の通る経路のことを「パス(path)」と呼び、衛星毎に番号が振られていますので、これを確認します。
また、衛星は地球の周りをぐるぐると回っているので北から南に下るパス(南行軌道)と南から北へ昇るパス(北行軌道)があり、この向きも合わせる必要があります。
②同じ観測モードであること
スマホのカメラにパノラマモードや高精細モードがあるのと同様に、SARセンサにも用途に合わせていくつかの観測モードがあり、それぞれで解像度や観測範囲が異なります。
今回扱うPALSAR-2の場合、大きく分けて以下の3種類の観測モードがあります。
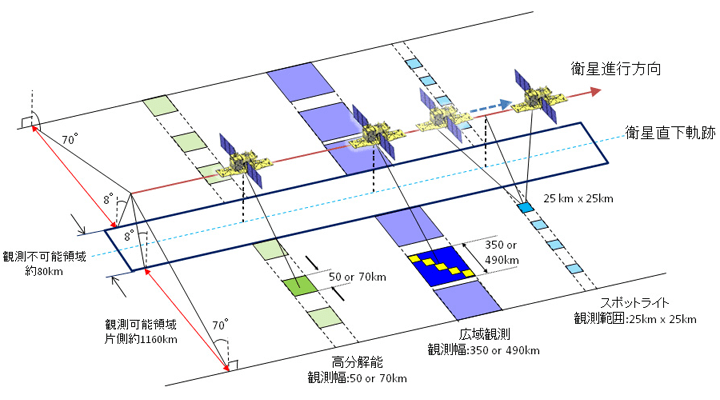
◆「スポットライトモード」
最も詳細な観測を実現する分解能1m×3m(観測域25km)
◆「高分解能モード」
分解能3m、6m、10mから選択可能(観測域50km or 70km)
◆「広域観測モード」
広範囲を一度に観測できる(分解能60m~100m、観測域350km or 490km)
可干渉ペアを探す際には、この観測モードも合わせる必要があります。
③観測時期が離れすぎていないこと
観測時期が離れすぎていると、部分的に地盤が動きながら、一部で植生が変わっていたりするなど複数の要因の影響を受ける可能性が高くなり、要因分解ができなくなるので注意が必要です。一般的には数か月の単位程度で比較が行われます。
では、上記の条件を満たす干渉ペアを実際に探していきます。
なお本記事では、元々平坦でなおかつ地盤変動測量の実例がある東京湾の埋め立て地にある某テーマパークを対象にしてみます。
※山間部など地形が複雑な地域では処理方法をより高度なものに変更する必要がありますので、注意してください
プロダクトの検索コード
まずは、希望の地点の緯度経度情報を入力して、プロダクトを検索します。その時、同時に可干渉の条件①と②で必要な軌道情報、観測モードなどを出力してみます。
import requests
TOKEN = "自分のAPIトークンを入れてください"
def search_palsar2_l11(params={}, next_url=''):
if len(next_url) > 0:
url = next_url
else:
url = 'https://file.tellusxdp.com/api/v1/origin/search/palsar2-l11'
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url,params=params, headers=headers)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
return r.json()
def main():
lat = 35.630
lon = 139.882
for k in range(100):
if k == 0:
ret = search_palsar2_l11({'after':'2017-01-01T15:00:00'})
else:
ret = search_palsar2_l11(next_url = ret['next'])
for i in ret['items']:
lon_min = i['bbox'][0]
lat_min = i['bbox'][1]
lon_max = i['bbox'][2]
lat_max = i['bbox'][3]
if lat > lat_min and lat lon_min and lon < lon_max:
print(i['dataset_id'],i['beam_number'],i['path_number'],i['frame_number'],i['mode'])
if 'next' not in ret:
break
if __name__=="__main__":
main()
このコードの実行結果は以下のようになっていると思います。

出力した情報のうち、”beam_number”, “path_number”, “frame_number”は、一種の軌道(位置・向き)の情報だと思ってください。これらが一致しないと、基本的に干渉させることはできません。東京湾が中心に位置している画像は、beam_number=U2-8, path_number=18, fram_number=2900となりますので、その条件で絞り込むことにします。
| 変数名 | 説明 | 格納例 |
| beam_number | 観測モードと衛星がどれくらい斜めに撮っているかの組み合わせ | 例)F2-5 |
| path_number | 衛星の通る経路 | 001~207 |
| frame_number | 撮影範囲の中心位置を示す | 0000~7190 |
詳しくは、JAXAのサイトをご覧ください。
また、”mode”とは、ALOS-2が持つ複数の観測モードであり、SM1はStripmap1(解像度3m), SM2はStripmap2(解像度6m)の画像になります。今回はせっかくなので、高い解像度のSM1のモードの画像を使ってみることにしましょう。
選んだ干渉ペアをまとめてダウンロードするスクリプトを以下に記載します。(以下、既出の関数は記載を省いています)
開発環境の空き容量が十分あること(30G程度)を確認してから実行してください。
import os
def publish_palsar2_l11(dataset_id):
url = 'https://file.tellusxdp.com/api/v1/origin/publish/palsar2-l11/{}'.format(dataset_id)
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url, headers=headers)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
return r.json()
def download_file(url, dir, name):
headers = requests.utils.default_headers()
headers["Authorization"] = "Bearer " + TOKEN
r = requests.get(url, headers=headers, stream=True)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
if os.path.exists(dir) == False:
os.makedirs(dir)
with open(os.path.join(dir,name), "wb") as f:
for chunk in r.iter_content(chunk_size=1024):
f.write(chunk)
def main():
for k in range(100):
if k == 0:
ret = search_palsar2_l11({'after':'2017-01-01T15:00:00'})
else:
ret = search_palsar2_l11(next_url = ret['next'])
for i in ret['items']:
if i['beam_number'] == 'U2-8' and i['path_number'] == 18 and i['frame_number'] == 2900 and i['mode'] == 'SM1':
dataset_id = i['dataset_id']
published = publish_palsar2_l11(dataset_id)
for file in published['files']:
file_name = file['file_name']
file_url = file['url']
print(file_name)
file = download_file(file_url, dataset_id, file_name)
if 'next' not in ret:
break
if __name__=="__main__":
main()この例では、5つのプロダクトが該当しました。カレントディレクトリに、プロダクトIDと同名のフォルダが作成され、その中にデータが保存されて、以下のようになっていると思います。これでまず干渉SARに必要なデータの取得が完了しました。なお観測日は、2018/3/22, 2018/3/22, 2018/6/28, 2018/10/18, 2018/11/29, 2019/3/21と、1年間で数カ月間隔のデータとなっています。
また、5つのプロダクトのサムネイル画像は以下の通りです。

Original data provided by JAXA
なお、ALOS-2の処理レベルL1.1では、画像が左右反転しています。これは次のステップで補正します。
(2) 強度画像と位相画像を出力
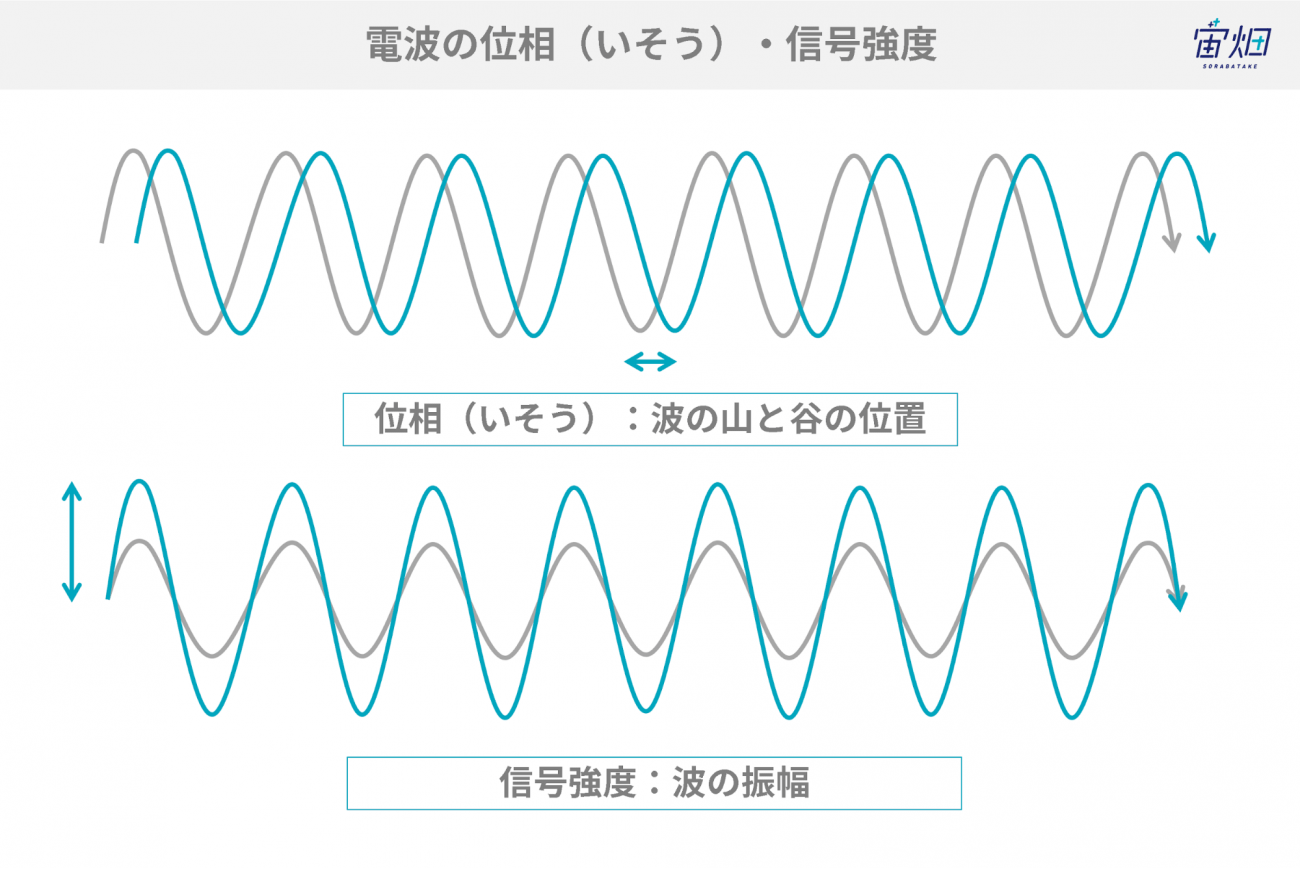
過去の記事(【コード付き】TellusでPALSAR-2のL1.1の 画像化にチャレンジしてみた)でもご紹介しましたが、 SAR画像は電波であるという特性から「強度」と「位相」という2つの情報を有しています。簡単に言うと、強度は「電波の跳ね返ってくる強さ」を位相は「電波の山と谷の位置」を表します。
それぞれのプロダクトから、強度画像と位相画像を出力してみます。画像全体では、サイズが大きすぎてメモリエラーとなるため、緯度経度を指定して、切り出すこととします。
import os
import numpy as np
import struct
import math
import matplotlib.pyplot as plt
from io import BytesIO
import cv2
def gen_img(fp,off_col,col,off_row,row):
cr = np.array([off_col,off_col+col,off_row,off_row+row],dtype="i4");
fp.seek(236)
nline = int(fp.read(8))
fp.seek(248)
ncell = int(fp.read(8))
nrec = 544 + ncell*8
nline = cr[3]-cr[2]
fp.seek(720)
fp.seek(int((nrec/4)*(cr[2])*4))
data = struct.unpack(">%s"%(int((nrec*nline)/4))+"f",fp.read(int(nrec*nline)))
data = np.array(data).reshape(-1,int(nrec/4))
data = data[:,int(544/4):]
data = data[:,::2] + 1j*data[:,1::2]
data = data[:,cr[0]:cr[1]]
sigma = 20*np.log10(abs(data)) - 83.0 - 32.0
phase = np.angle(data)
sigma = np.array(255*(sigma - np.amin(sigma))/(np.amax(sigma) - np.amin(sigma)),dtype="uint8")
sigma = cv2.equalizeHist(sigma)
return sigma, phase
def get_pl(fp,latlon):
fp.seek(720+4096+1620+4680+16384+9860+325000+511000+3072+728000+2064,0)
c = np.zeros(25,dtype="float64")
for i in range(25):
c[i] = fp.read(20)
d = np.zeros(25,dtype="float64")
for i in range(25):
d[i] = fp.read(20)
lat0 = float(fp.read(20))
lon0 = float(fp.read(20))
phi = np.zeros(2,dtype="float64")
lam = np.zeros(2,dtype="float64")
phi[0] = latlon[0] - lat0
phi[1] = latlon[1] - lat0
lam[0] = latlon[2] - lon0
lam[1] = latlon[3] - lon0
pl = np.zeros(4,dtype="float64")
for i in range(5):
for j in range(5):
id = i*5+j
pl[0] += c[id]*lam[0]**(4-j) * phi[0]**(4-i)
pl[1] += c[id]*lam[1]**(4-j) * phi[1]**(4-i)
pl[2] += d[id]*lam[0]**(4-j) * phi[0]**(4-i)
pl[3] += d[id]*lam[1]**(4-j) * phi[1]**(4-i)
return pl
def main():
#合計5つのプロダクトに対して同じ処理を行ってください
ids = ['ALOS2206702900-180322',
'ALOS2221192900-180628',
'ALOS2237752900-181018',
'ALOS2243962900-181129',
'ALOS2260522900-190321']
for i, dataset_id in enumerate(ids):
fpimg = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-UBSR1.1__D'),mode='rb')
fpled = open(os.path.join(dataset_id,'LED-'+dataset_id+'-UBSR1.1__D'),mode='rb')
latlon = np.array([35.625, 35.640, 139.86, 139.90],dtype="float64")
pl = np.array(np.ceil(get_pl(fpled,latlon)),dtype=np.int64)
print(pl)
off_col = pl[1]
col = pl[0] - pl[1]
off_row = pl[3]
row = pl[2] - pl[3]
print(col,row)
sigma, phase = gen_img(fpimg,off_col,col,off_row,row)
sigma = np.fliplr(sigma) #左右反転
phase = np.fliplr(phase) #左右反転
np.save('sigma0{}.npy'.format(i + 1),sigma) #numpy配列として出力
np.save('phase0{}.npy'.format(i + 1),phase) #numpy配列として出力
# 画像の保存
plt.imsave('sigma0{}.jpg'.format(i + 1), sigma, cmap = "gray")
plt.imsave('phase0{}.jpg'.format(i + 1), phase, cmap = "jet")
dataset_id = 'ALOS2206702900-180322'
# dataset_id = 'ALOS2221192900-180628' #合計5つのプロダクトに対して
# dataset_id = 'ALOS2237752900-181018' #同じ処理を行ってください。
# dataset_id = 'ALOS2243962900-181129'
# dataset_id = 'ALOS2260522900-190321'
fpimg = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-UBSR1.1__D'),mode='rb')
fpled = open(os.path.join(dataset_id,'LED-'+dataset_id+'-UBSR1.1__D'),mode='rb')
latlon = np.array([35.625, 35.640, 139.86, 139.90],dtype="float64")
pl = np.array(np.ceil(get_pl(fpled,latlon)),dtype=np.int64)
print(pl)
off_col = pl[1]
col = pl[0] - pl[1]
off_row = pl[3]
row = pl[2] - pl[3]
print(col,row)
sigma, phase = gen_img(fpimg,off_col,col,off_row,row)
sigma = np.fliplr(sigma) #左右反転
phase = np.fliplr(phase) #左右反転
np.save('sigma01.npy',sigma) #numpy配列として出力
np.save('phase01.npy',phase) #numpy配列として出力
#np.save('sigma02.npy',sigma) #numpy配列として出力
#np.save('phase02.npy',phase) #numpy配列として出力
#np.save('sigma03.npy',sigma) #numpy配列として出力
#np.save('phase03.npy',phase) #numpy配列として出力
#np.save('sigma04.npy',sigma) #numpy配列として出力
#np.save('phase04.npy',phase) #numpy配列として出力
#np.save('sigma05.npy',sigma) #numpy配列として出力
#np.save('phase05.npy',phase) #numpy配列として出力
if __name__=="__main__":
main()
これによって得られた画像は以下の通りです。

Original data provided by JAXA
強度画像は、電波を反射する強さを表す反射係数を校正して対数化しています。また、位相画像は、-180度~+180度(-π~+π)の範囲で表現しています。
3m解像度のため、強度画像では建物が判別できるレベルの視認性を有しています。一方で、位相画像は、これだけではまったく視認性がありません。
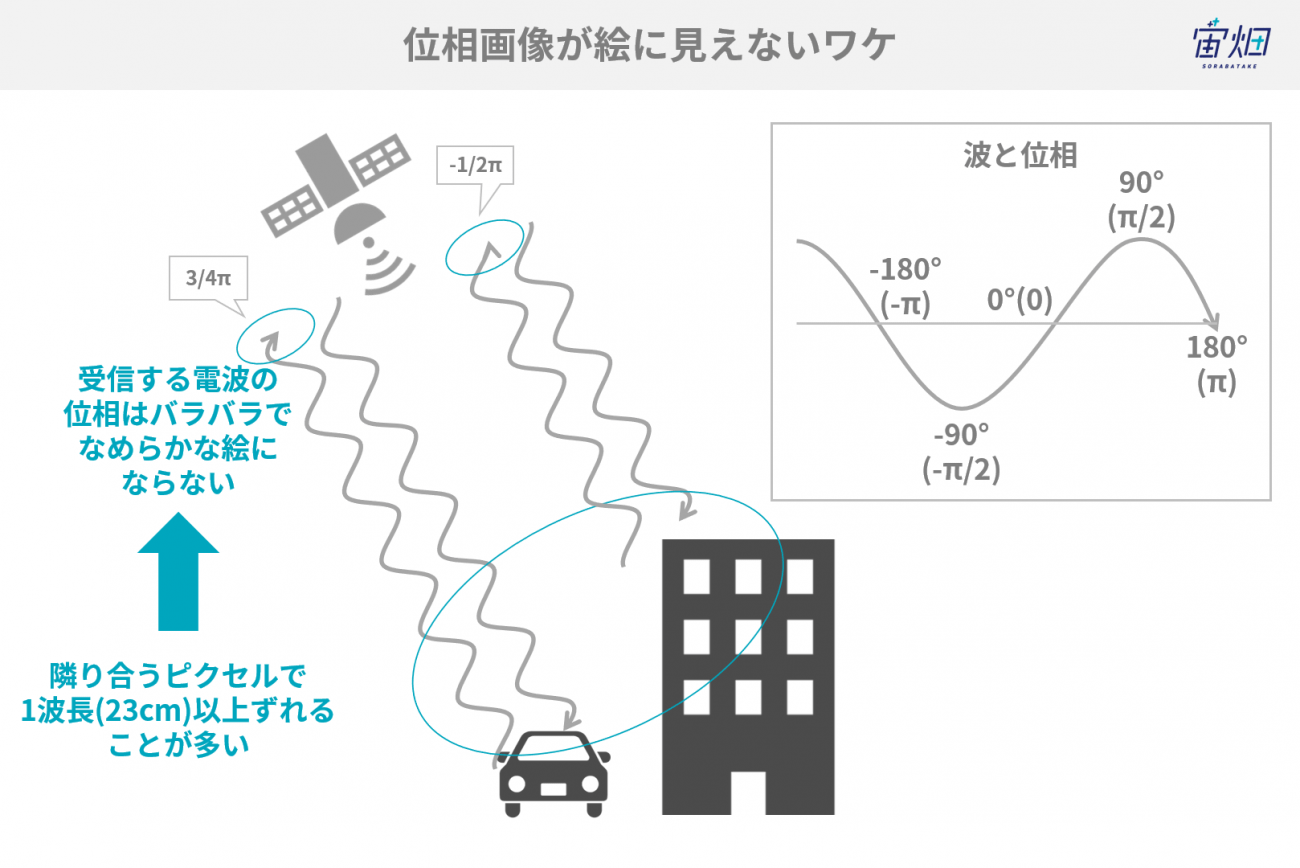
それもそのはずで、PALSAR-2の電波の波長は23cm程度なので、3m解像度では、隣接するピクセルの間に1波長以上のアンビギュイティ(曖昧さ)が存在してしまうので、隣接するピクセルで相関がほとんどないためです。
SARにおいて、波長よりも十分短い解像度で観測するということは非常に困難なため、「一つの位相画像における位相情報には意味がない」ということを覚えてくと良いでしょう。だからこそ、干渉させることに意味があるということになります。
上記のプログラムを用いて、5つのプロダクトすべての、強度画像と位相画像を、numpy配列として出力してください。そして次のステップ、いよいよ干渉解析を実施していきましょう。
(3)画像の位置合わせと干渉処理
これまで、「干渉」「干渉」と言ってきましたが、実際に何をしているのか、イメージがわかない方も多いと思います。やっていることは、主に以下の2つのステップです。
①2つの強度画像を用いて、画像の位置合わせを行う
②2つの位相画像の差分をとり、[-π~+π]にラップ※する
※[-π~+π] – [-π~+π] = [-2π~+2π]となるので、それを[-π~+π]に戻す処理を言います
特に重要なのが①の位置合わせです。2つの画像を、精度よく重ね合わせることで、より良い結果が得られます。
この位置合わせについては様々な手法が存在し、強度画像を使ってサブピクセル(1ピクセル未満)レベルの位置合わせを行い、位相画像の補間処理をするのが一般的です。
ただし今回は、干渉のために必要最低限のシンプルなアルゴリズムで、1ピクセルレベルでの位置合わせを実施し、2つの画像が重ならない部分をカットすることとします。単純な平行移動だけなので、Tellus環境で使用可能なOpenCVというライブラリにある機能を使うことにします。
②の処理はただの引き算です。この瞬間がまさに、“干渉”と言えます。また、これもまた一般的な話ですが、普通は、強度成分も含めた2つの複素画像に対して、片方の複素共役をもう片方に乗算する操作のことを干渉処理と言いますが、やっていることは全く同じです。本記事では、初学者にわかりやすいように、最初から強度と位相の情報を分けて取り扱っているので、「干渉処理は位相の差分を取ること」と覚えていただければ十分です。
また、今回は、5つのプロダクトがあるので、中央のNo.3をリファレンスとして、他の4つの画像に対して干渉させてみることにしました。
import os
import numpy as np
import matplotlib.pyplot as plt
import math
from io import BytesIO
import cv2
#画像の位置合わせを行う関数
#強度画像A,Bを用いて変位量を求めて、位相画像C,Dをその変位量で画像をカットします
#変位量は小数点以下まで結果がでますが、それを四捨五入して整数として扱っています
def coregistration(A,B,C,D):
py = len(A)
px = len(A[0])
A = np.float64(A)
B = np.float64(B)
d, etc = cv2.phaseCorrelate(B,A)
dx, dy = d
print(d) #画像の変位量です
if dx = 0:
dx = math.ceil(dx)-1
dy = math.ceil(dy)
rD = D[dy:py,0:px+dx]
rC = C[dy:py,0:px+dx]
elif dx < 0 and dy = 0 and dy = 0 and dy >= 0:
dx = math.ceil(dx)
dy = math.ceil(dy)-1
rD = D[dy:py,dx:px]
rC = C[dy:py,dx:px]
return rC, rD
def wraptopi(x):
x = x - np.floor(x/(2*np.pi))*2*np.pi - np.pi
return x
def main():
#強度画像と位相画像の読み込み。また、ここで画像のサイズを統一しています。
phase01 = np.load('phase01.npy')[0:1028,0:1420]
sigma01 = np.load('sigma01.npy')[0:1028,0:1420]
phase02 = np.load('phase02.npy')[0:1028,0:1420]
sigma02 = np.load('sigma02.npy')[0:1028,0:1420]
phase03 = np.load('phase03.npy')[0:1028,0:1420]
sigma03 = np.load('sigma03.npy')[0:1028,0:1420]
phase04 = np.load('phase04.npy')[0:1028,0:1420]
sigma04 = np.load('sigma04.npy')[0:1028,0:1420]
phase05 = np.load('phase05.npy')[0:1028,0:1420]
sigma05 = np.load('sigma05.npy')[0:1028,0:1420]
#プロダクトNo.1とNo.3で干渉処理を実施
coreg_phase01, coreg_phase03 = coregistration(sigma01,sigma03,phase01,phase03)
ifgm01 = wraptopi(coreg_phase01 - coreg_phase03)
#プロダクトNo.2とNo.3で干渉処理を実施
coreg_phase02, coreg_phase03 = coregistration(sigma02,sigma03,phase02,phase03)
ifgm02 = wraptopi(coreg_phase02 - coreg_phase03)
#プロダクトNo.4とNo.3で干渉処理を実施
coreg_phase04, coreg_phase03 = coregistration(sigma04,sigma03,phase04,phase03)
ifgm04 = wraptopi(coreg_phase04 - coreg_phase03)
#プロダクトNo.5とNo.3で干渉処理を実施
coreg_phase05, coreg_phase03 = coregistration(sigma05,sigma03,phase05,phase03)
ifgm05 = wraptopi(coreg_phase05 - coreg_phase03)
np.save('ifgm01.npy',ifgm01)
np.save('ifgm02.npy',ifgm02)
np.save('ifgm04.npy',ifgm04)
np.save('ifgm05.npy',ifgm05)
#画像の保存
plt.imsave('ifgm01.jpg', ifgm01, cmap = "jet")
plt.imsave('ifgm02.jpg', ifgm02, cmap = "jet")
plt.imsave('ifgm04.jpg', ifgm04, cmap = "jet")
plt.imsave('ifgm05.jpg', ifgm05, cmap = "jet")
if __name__=="__main__":
main()
これによって出力された干渉画像(以下インターフェログラムと言います)は以下の通りです。
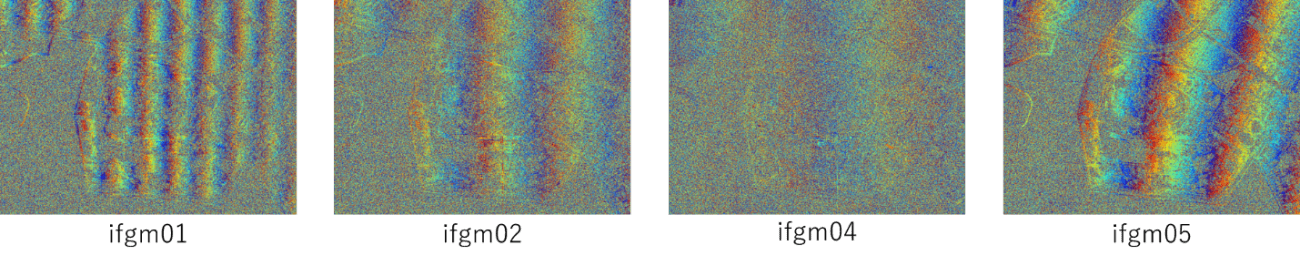
Original data provided by JAXA
キレイな縞模様が見えますね。これが、干渉によって生じる「干渉縞」です。しかも、4枚のインターフェログラムでそれぞれに形が異なります。これについては後ほど詳細を説明します。
位置合わせを1ピクセルレベルで行った割には、十分に干渉していると言えます。縞模様が判別できないところは、主に水面部分で、ここは干渉性が低い(コヒーレンスが低い)地点になります。
今回は、4つのペアでインターフェログラムを作成したのですが、一番左(ifgm01)と一番右(ifgm05)では縞模様が比較的はっきりしていますね。次章以降では、この二つのデータを用いることとします。残りのふたつは、恐らく位置合わせの精度が十分でなく、干渉性が低かったのだと考えられます。
しかしながら、この画像だけでは、まだ何も価値のある情報が抽出できません。ここからさらに、ひと手間を加える必要があります。それは、干渉縞を削除することです。
(4)軌道縞を削除し地形の変化情報を抽出する
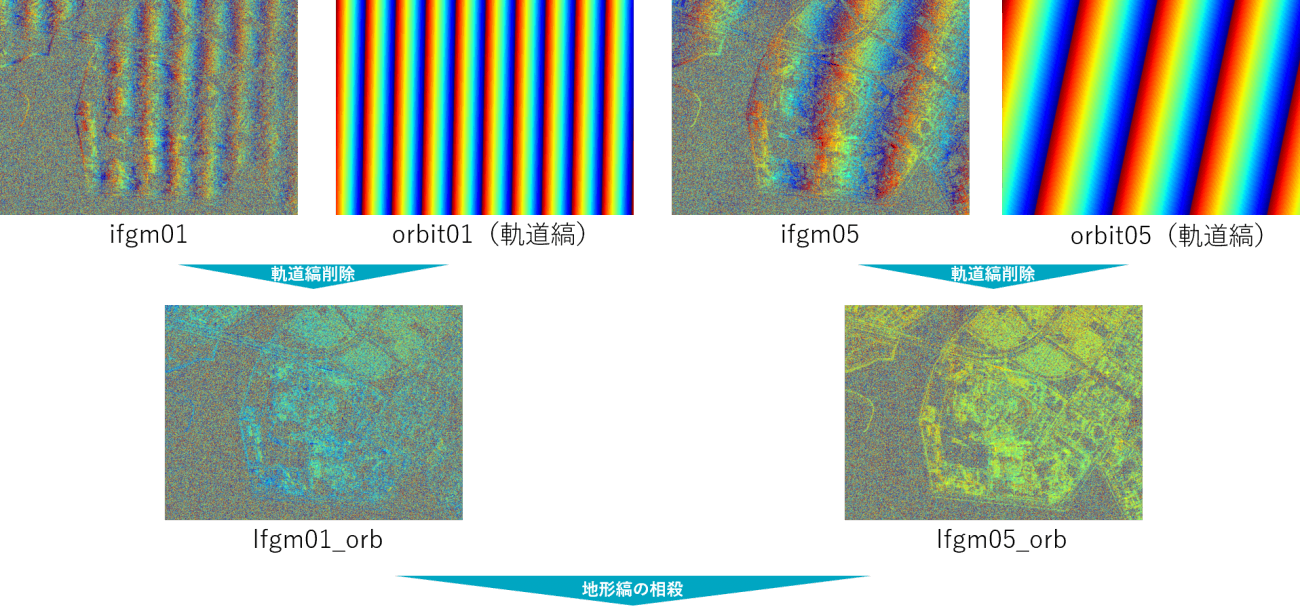
まず、干渉縞について説明します。干渉縞には2種類あって、ひとつは、山などで地形が起伏していることに由来する、「地形縞」と呼ばれるものです。これを削除するには、一般的には従来のデジタル標高モデル(DEM)を用いて地形縞を作成し、インターフェログラムから削除します。ただし今回は、DEMは用いずに、2枚のインターフェログラムを用いて地形縞を削除する手法を用います。
もうひとつ、干渉縞に含まれる成分として、「軌道縞」というものがあります。これは、2回の観測時の衛星の位置が微妙に違うことによって生じる縞模様です。したがって、前章のように、すべてのインターフェログラムにおいて、ペアとなる衛星の位置の組み合わせがそれぞれ異なるので、異なる軌道縞が生じることになります。
つまり、「干渉縞には、地形縞と軌道縞が含まれている」ということを理解していただければと思います。この両方を、インターフェログラムからキレイに削除すると、2時期における地形の変化成分を抽出することができます。

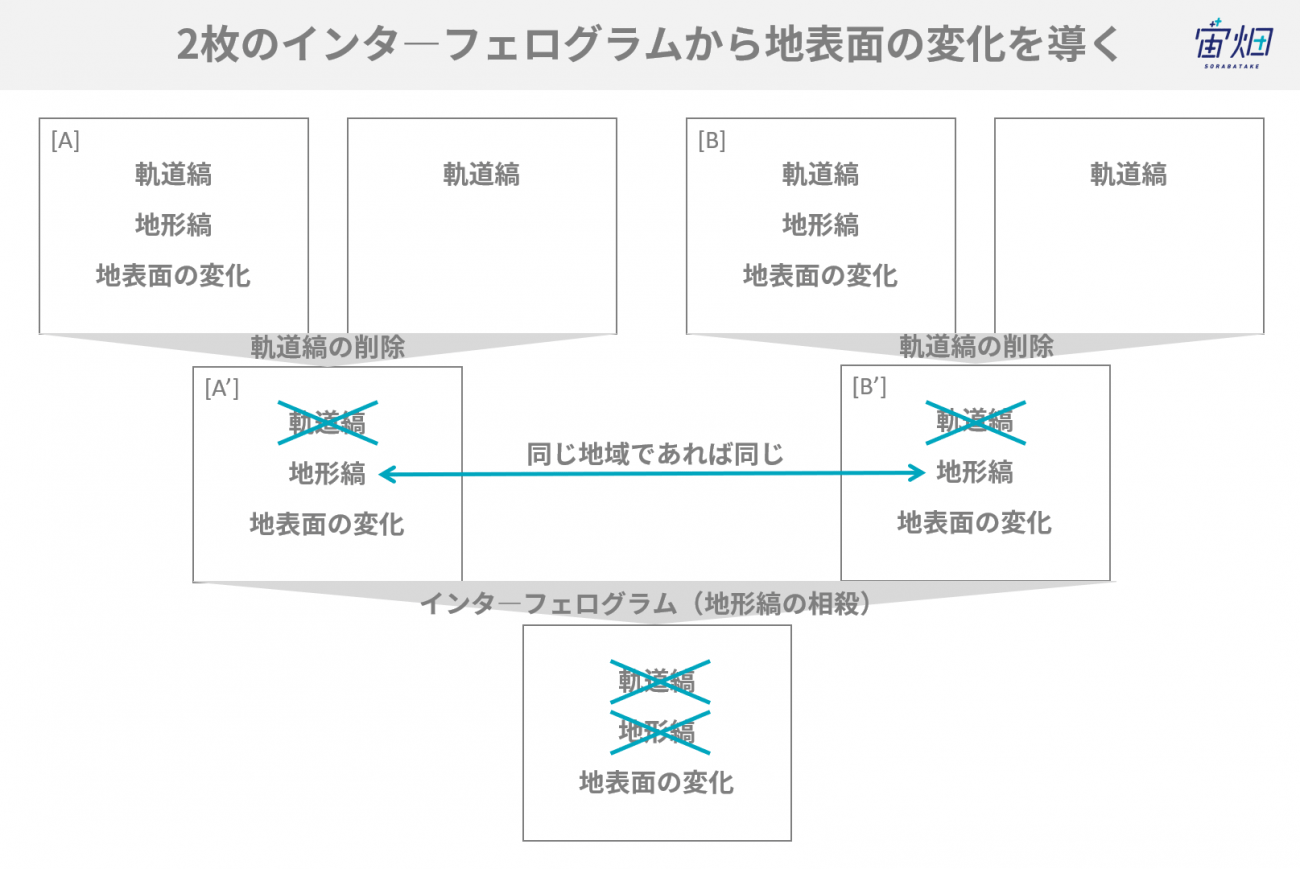
地形縞だけを削除すると、軌道縞だけが残り、軌道縞だけを削除すると地形縞だけが残る、という関係があります。この関係を使って、DEMなどの外部の情報を使用せずに、地表面の変化を抽出することができます。
すなわち、2つのインターフェログラムを用意して、ひとつ目のインターフェログラムAから地形縞は残したまま、軌道縞だけを削除します(A’)。そしてもうひとつのインターフェログラムBからも同様に地形縞を残したまま、軌道縞を削除します(B’)。ここまでの処理でA’とB’にはどちらも地形縞が残っています。この地形縞は、地形によるものなので、A’とB’で共通です。したがって、A’とB’でもう一度インタ―フェログラムの処理をすれば、地形縞は相殺されます。この場合、軌道縞を削除するアルゴリズムだけがあれば良いので、処理が楽になります。
今回はこの方法を使って、地形の変化を抽出してみましょう。軌道縞を削除するには、文字通り軌道情報を用いることが一番効果的です。しかしながら、ここも簡単に実施するため、少々アナログな方法ではありますが、平面の一次方程式の係数を調整して、軌道縞を作って削除することにします。
import numpy as np
import matplotlib.pyplot as plt
def gen_orb(nx,ny,a,b):
orb = np.zeros([ny,nx])
for iy in range(ny):
for ix in range(nx):
orb[iy,ix] = a*iy+b*ix
orb = wraptopi(orb)
return orb
def main():
#インターフェログラムの入力。相感度の強かった01と05を使用する
ifgm01 = np.load('ifgm01.npy')
ifgm05 = np.load('ifgm05.npy')
ny = ifgm05.shape[0]
nx = ifgm05.shape[1]
#軌道縞の生成
orbit01 = gen_orb(nx,ny,-0.00085,-0.044)
orbit05 = gen_orb(nx,ny,-0.0036,-0.017)
#軌道縞の削除(3π/4の係数は、画像の中央値を0に近づけるための補正値)
ifgm01_orb = wraptopi(ifgm01 - orbit01 - np.pi*3/4.)
ifgm05_orb = wraptopi(ifgm05 - orbit05 + np.pi*3/4.)
#軌道縞を削除した画像とで差分干渉処理を行い、地形の変化成分を抽出
difgm = wraptopi(ifgm01_orb - ifgm05_orb - np.pi*3/4.0)
#画像の保存
plt.imsave('orbit01.jpg', orbit01, cmap = "jet")
plt.imsave('orbit05.jpg', orbit05, cmap = "jet")
plt.imsave('ifgm01_orb.jpg', ifgm01_orb, cmap = "jet")
plt.imsave('ifgm05_orb.jpg', ifgm05_orb, cmap = "jet")
plt.imsave('difgm.jpg', difgm, cmap = "jet")
if __name__=="__main__":
main()このプログラムによって生成された画像を以下に示します。

Original data provided by JAXA
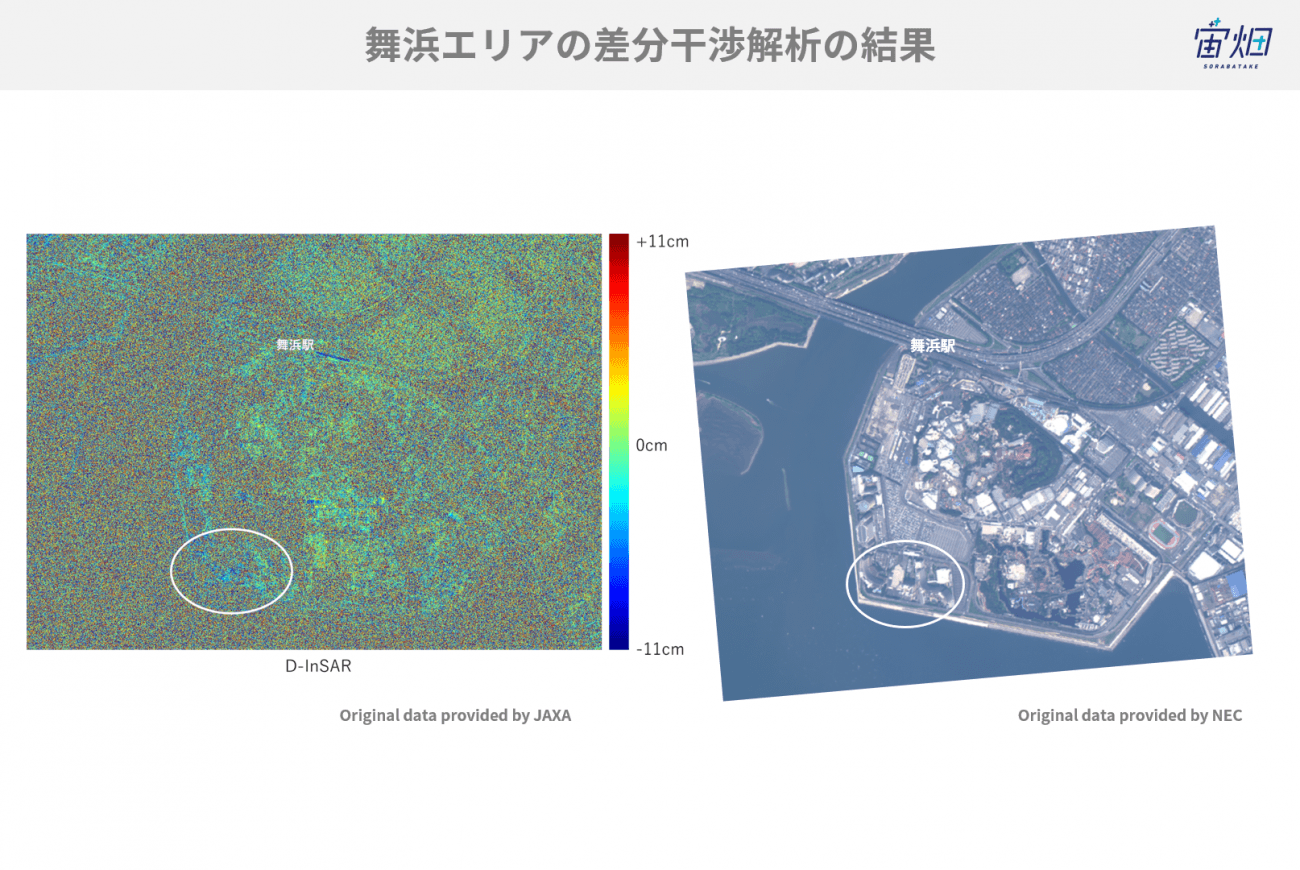
最後の干渉処理によって相感度が低下し、視認性が悪くなってしまっていますが、舞浜駅付近を基準として見た時(緑=0cm)、白枠のエリア周辺では少し青っぽくなっており、数cm程度地盤が沈下しているように見受けられます。ちなみに、プロダクトのNo.1とNo.5は、それぞれ18/03/22と19/3/21で、ちょうど1年になります。
国土地理院によると時期は異なりますが、数cmの地盤沈下は実際に起きているという報告がありますので、近い結果が得られたと言えるでしょう。
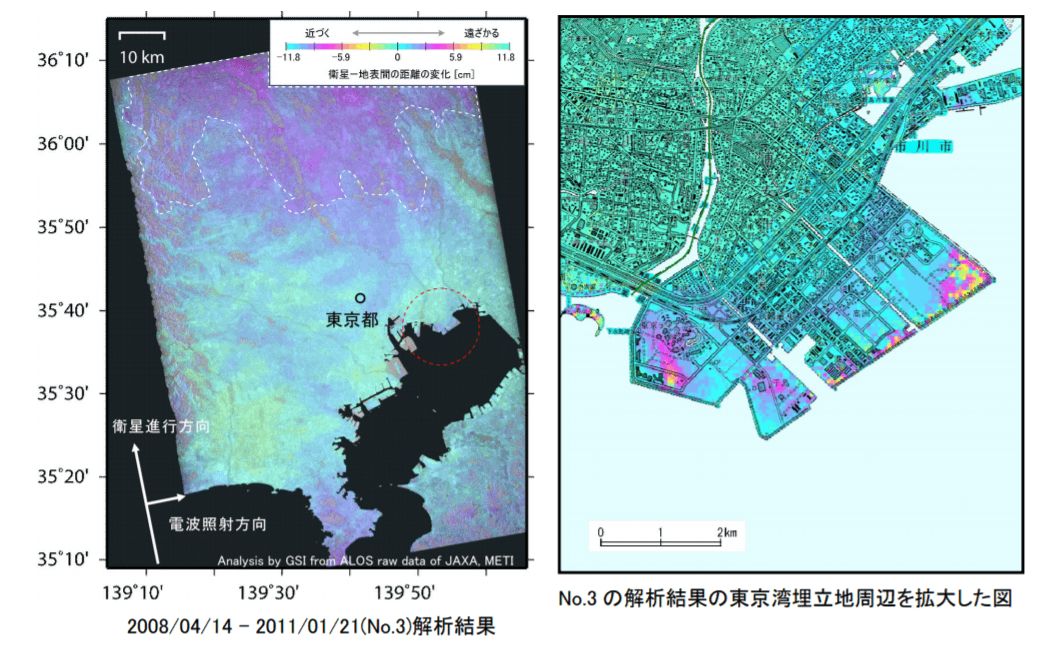
https://vldb.gsi.go.jp/sokuchi/sar/result/sar_data/report/H23_kanshi.pdf
まとめ
最後に、干渉SARの処理フローを再掲します。今回紹介したアルゴリズムは、非常に簡易なものであり、研究用や商用ソフトのレベルではありません。しかしながら、あとはこのフローに従ってそれぞれのアルゴリズムを自分流にアップグレードしていけば、オリジナルの干渉SARアプリケーションが作成可能になります。

ぜひ皆さんも、Tellusを活用して干渉SARを実践して、それぞれのビジネスや研究へ活用していただければ幸いです。
「Tellus」で衛星データを触ってみよう!
日本発のオープン&フリーなデータプラットフォーム「Tellus」で、まずは衛星データを見て、触ってみませんか?
★Tellusの利用登録はこちらから


