宙畑ではこれまで衛星観測技術であるSAR（サー）について何度かご紹介をしてきました。

電磁波を使って能動的に観測を行うことによって、雨や雲などの気象条件に左右されずに観測を行うことが強みで、現在様々なシーンで利用が進んでいる技術の一つです。

しかし、実際にSAR画像を見てみると白黒のざらざらした画像であり、一般的に用いられる画像とは大きく異なるため、「自分で使ってみるにはちょっと難しいかも」と思っていらっしゃる人も多いのではないでしょうか。

光学画像とSAR画像は例えるなら、ヒトの視覚と触覚に相当します。

SAR画像はただの白黒画像に見えますが、データの中には対象物の表面状態が分かる情報を有しており、適切に取り扱うことでそれらの新しい情報を取り出すことができるのです。

この処理のことを「偏波の成分分解」と言います。

偏波の成分分解を活用することで、土地被覆分類や物体識別の精度向上に役立てられます。

また、この処理は構造物と自然物を選り分けるだけでなく、SAR画像を扱いやすくするための処理だとも考えられます。

SAR画像を扱いやすくするための処理は、ノイズを除去するなど余計なものを削除するものは数多くありますが、今回のアプローチは画像全体に新しい情報を付加することができるので、画像の前処理として非常に有効です。

この技術は、今後発展的なSAR画像解析を行う上でも非常に重要な技術となるため、少しディープな内容にはなりますが、是非お読みいただけると幸いです。

今回の記事では、偏波の成分分解を用いて、Tellusで実際に構造物と自然物を選り分けることが出来るのかを検証していきたいと思います。

SAR画像からテクスチャ情報を取り出す「偏波の成分分解」

SARの白黒画像は「強度画像」

SAR画像としてよく見るのは、白黒の画像だと思います。
これは、観測対象物から跳ね返ってきた電磁波の強度(Intensity)を白黒で表現した画像です。

右側は水で構成されており、水は鏡面反射し衛星の方向にはほとんど返ってこないため真っ暗に写っています。左側は構造物が沢山あり、レーダを強く反射するため光っている(強度が強い)ことが確認できます。

電磁波の挙動：散乱（scattering）と反射(reflection)

散乱と反射という言葉を整理しておきます。

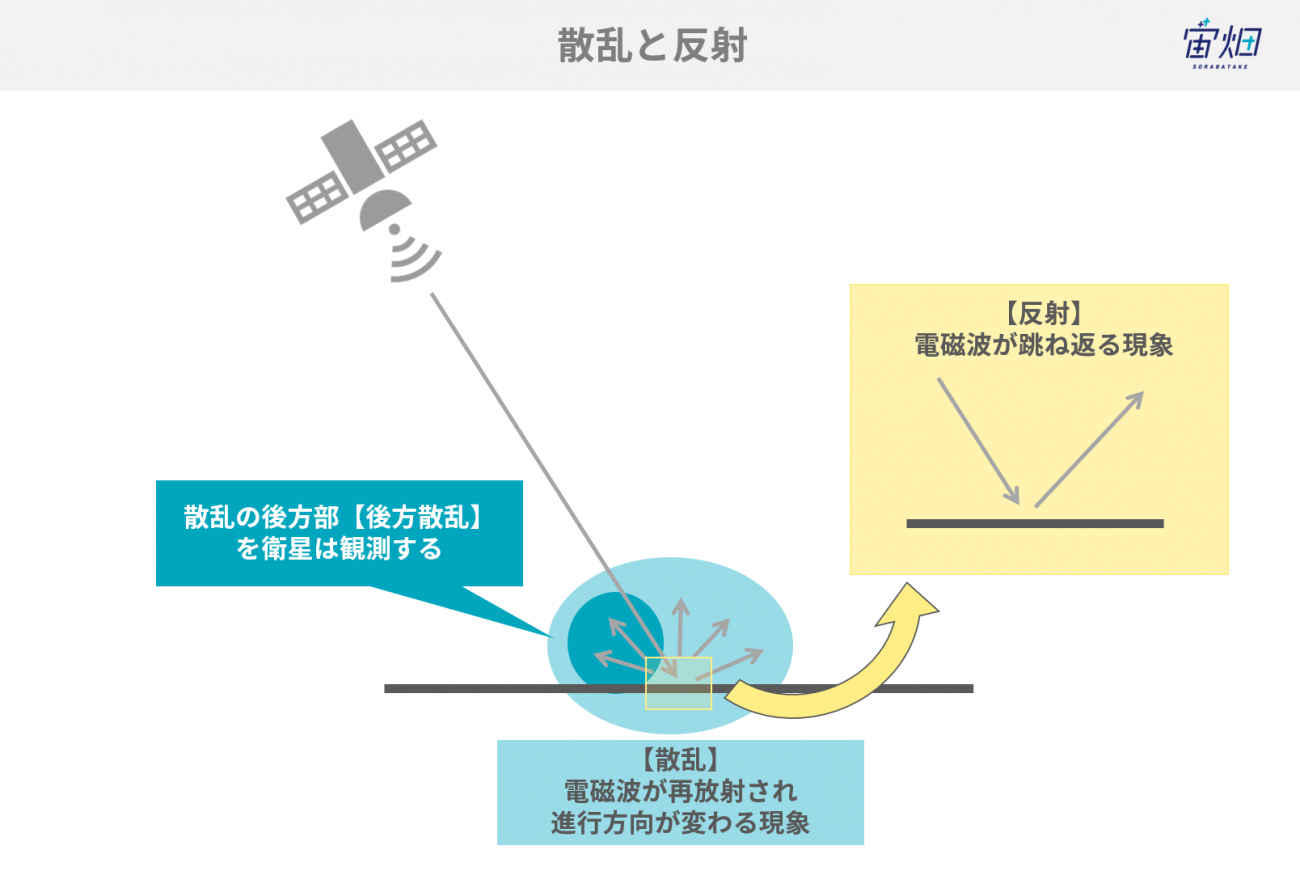
散乱（scattering）とは、電磁波が物体に入射した時、入射波のエネルギーの一部が電磁波として再放射され、電磁波の進行方向が乱れる過程のことを言います。

異なる電気的特性をもつ物体に入射するため、散乱は電磁波の反射や屈折といった現象を引き起こす要因になっています。

反射(reflection)は、単純に電磁波が跳ね返ることを反射といいます。

ここで、散乱したものの中で、入射の方向に対して(拡散)反射したものを後方散乱といいます。SAR画像は後方散乱された電磁波を画像化したのものです。

SARの様々な散乱プロセス～鏡面反射、コーナー反射、表面散乱、体積散乱～

この時、衛星から発せられた電磁波がどのような挙動をしているのかを考えてみます。

観測対象によって跳ね返り方、すなわち電磁波の散乱プロセスは様々です。以下に代表的な4種類の挙動をご紹介します。

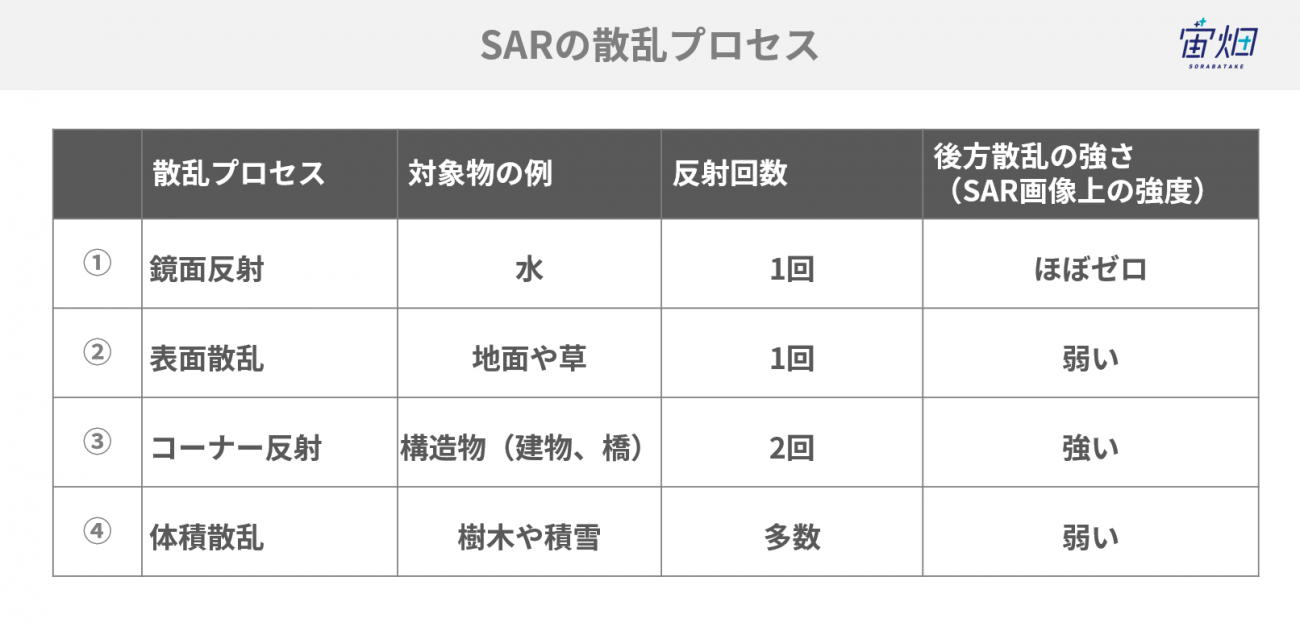
「反射回数」と「後方散乱（SAR画像上の強度）」を、SAR画像から読み解くことができるので、対象物が何かを識別できるということになります。

ただし、①の鏡面反射は後方散乱をほぼしないため、今回の偏波解析では、識別することはできません。

以下で詳しくそれぞれのプロセスについて説明していきます。

①鏡面反射＜水など滑らかかつ水平な平面＞

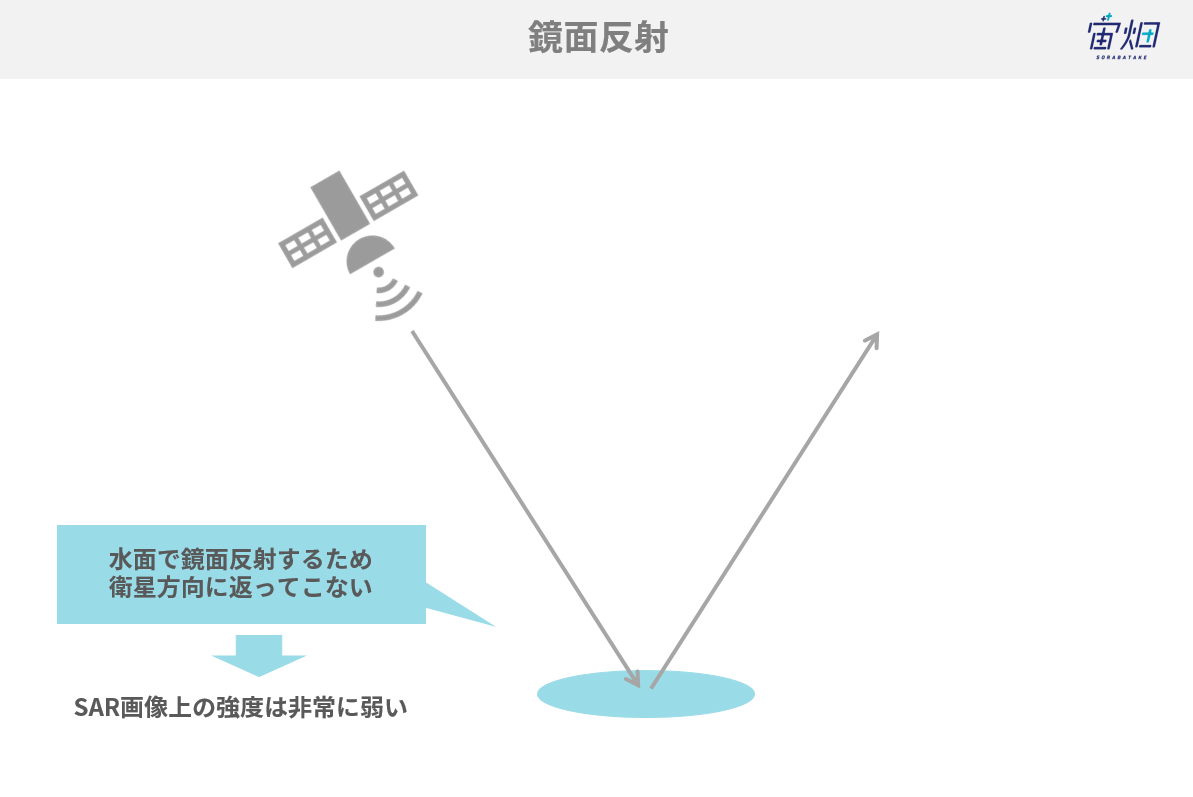
電磁波は滑らかな水面で鏡面反射を起こし、衛星にほとんど返ってきません。その結果として暗く写り(信号強度が低い)ます。

電波の反射回数としては1回となります。

②表面散乱＜地面や草など＞

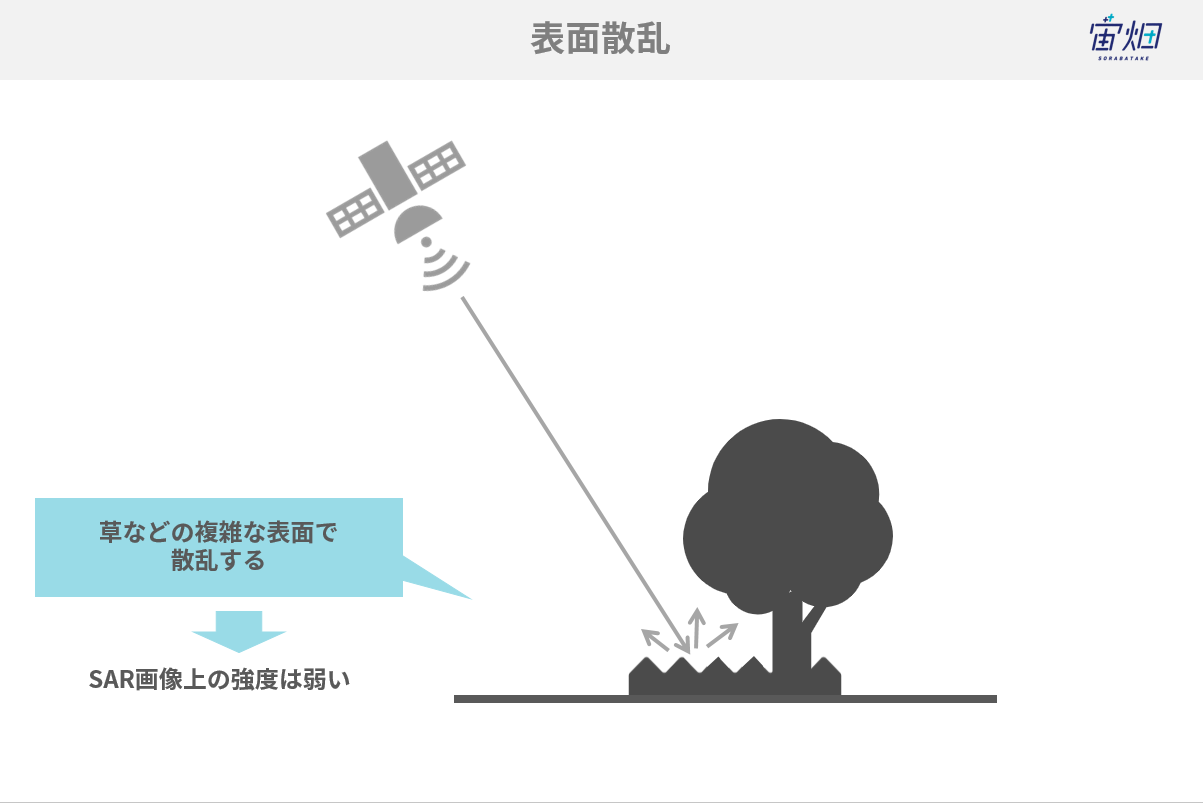
地面や草などで電磁波が反射すると、複雑な表面で電磁波は様々な方向にバラバラの強度で散乱します。これを表面散乱（surface scattering）と言います。表面散乱を起こした電磁波は、部分的にしか衛星に返っていかないため、そこまで強い信号強度を得られません。

表面散乱は一回反射となります。

③コーナー反射＜構造物（建物、橋など）＞

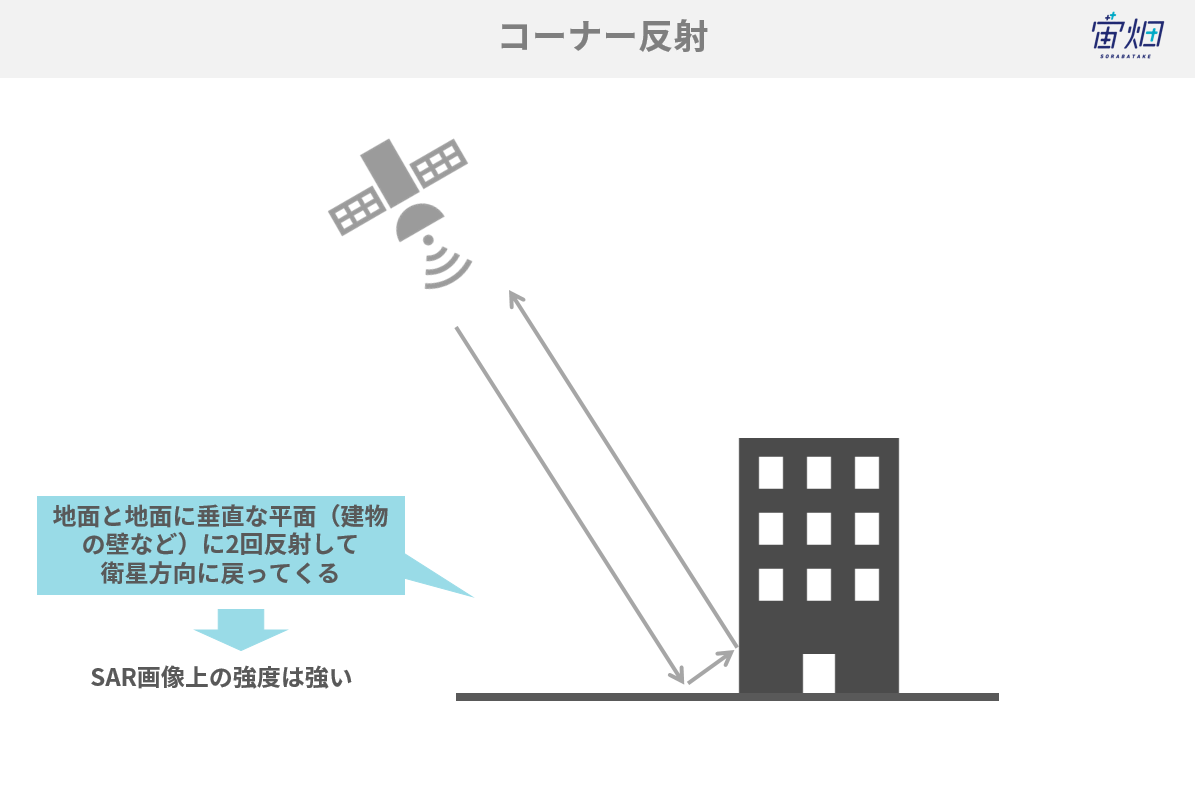
建物など地表面に対し垂直に立った平面があると、電磁波は地表面で反射した後、さらに建物の壁で反射し、衛星方向へ戻っていきます。これを2回反射と言います。

入ってきた電磁波のほとんどが戻っていくため、強い信号で衛星まで返っていきます。

④樹木や積雪など＜体積散乱＞

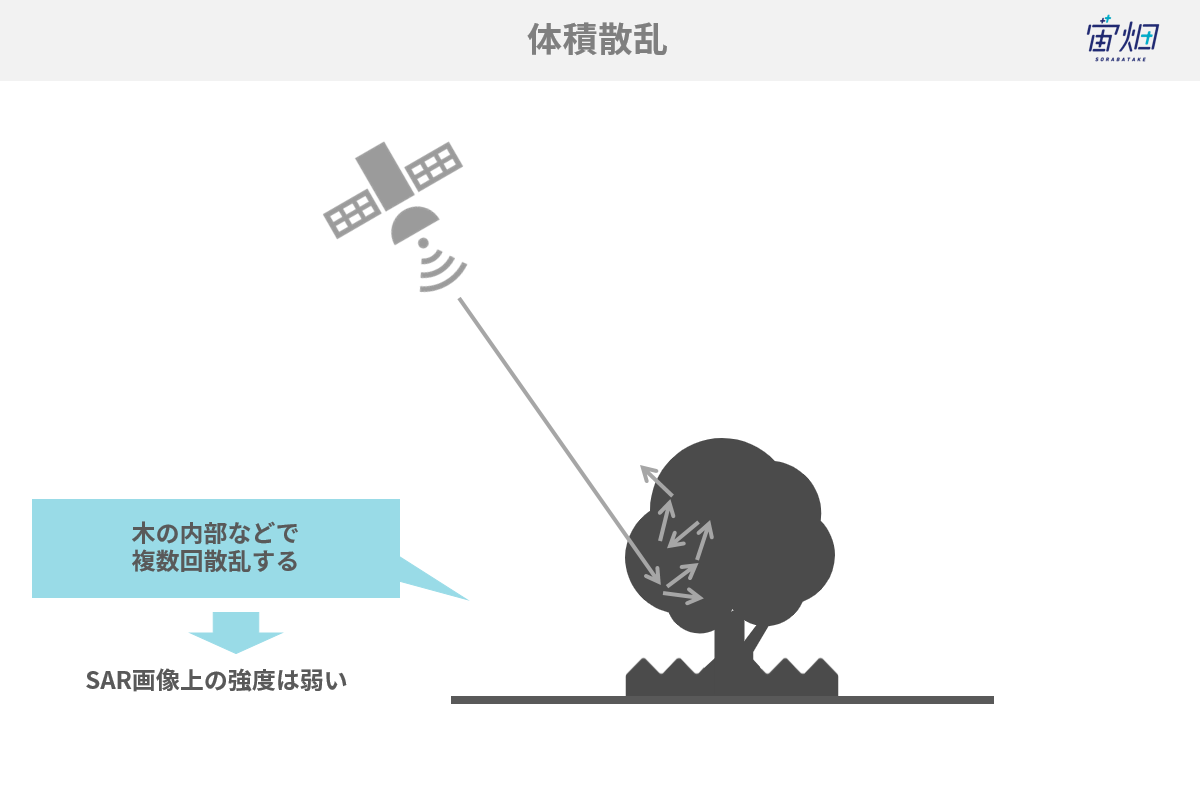
木に入射した電磁波も、葉っぱや枝等で複数回反射(体積散乱)を起こし、部分的にしか衛星に返っていかず、強い信号強度を得られません。この現象は樹木や積雪等で多くみられます。

表面散乱と体積散乱の大きな違いはその反射の回数です。先ほどの表面散乱は一回だったのに対し、体積散乱は複数回の反射を伴います。

偏波を使うと、反射や散乱が分類できる

ここまでご紹介してきた反射や散乱の種類ですが、これらはSAR観測特有の「偏波」を利用すると分類することができます。

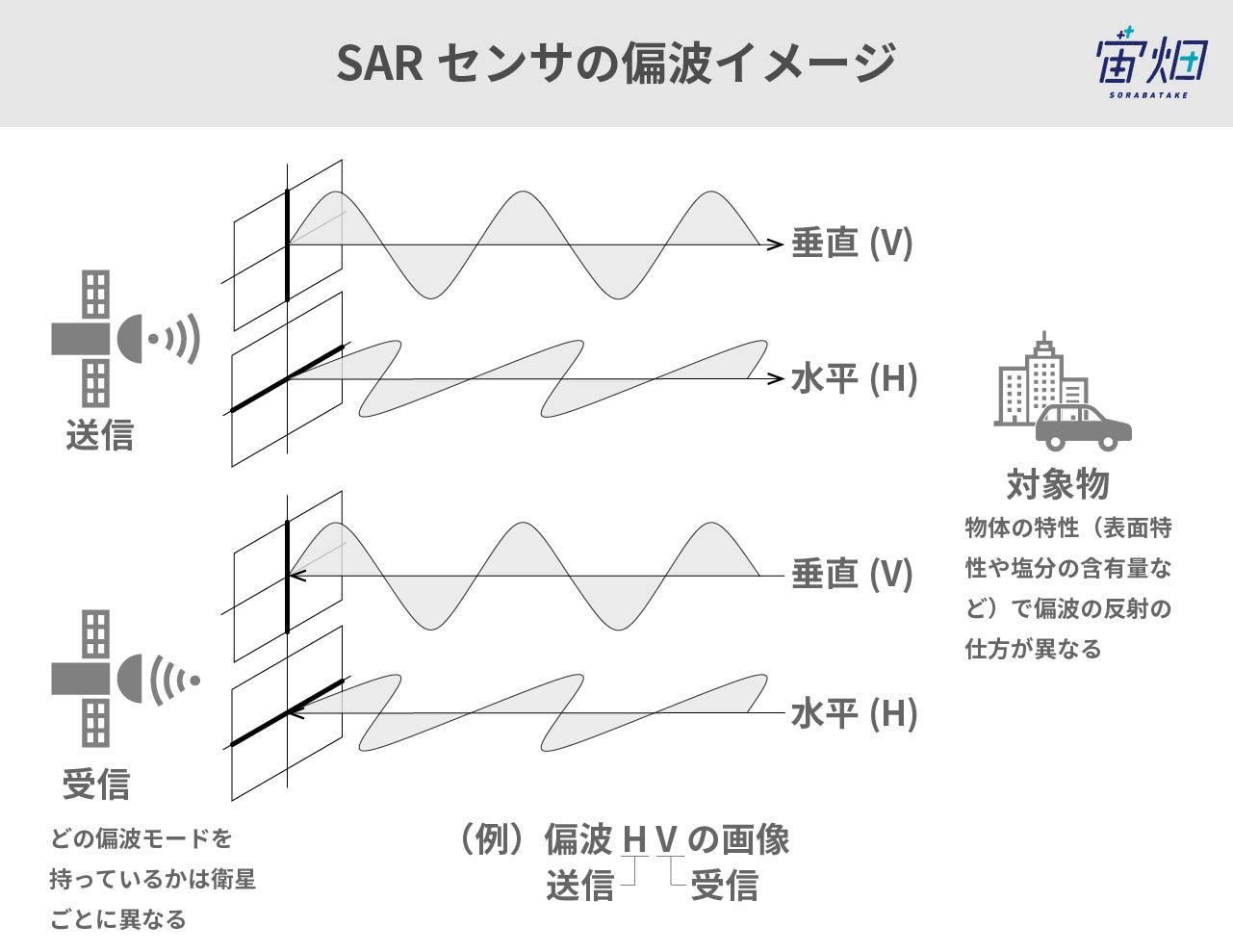
SARの電磁波は上図に示すようにその振動方向によって、垂直偏波・水平偏波に分けられます。

水平偏波Horizontal(H)もしくは垂直偏波Vertical(V)を発信し、反射して返ってきた電磁波を水平(H)、または垂直(V)で受信します。

水平偏波で電磁波を出して水平で受けることをHH、垂直で受けることをHVといい、垂直偏波で電磁波を出して、垂直で受けることをVV、水平で受けることをVHと言います。大きな衛星では、水平と垂直の両方を同時に受けられるものもありHH-HVなどと記述されます。

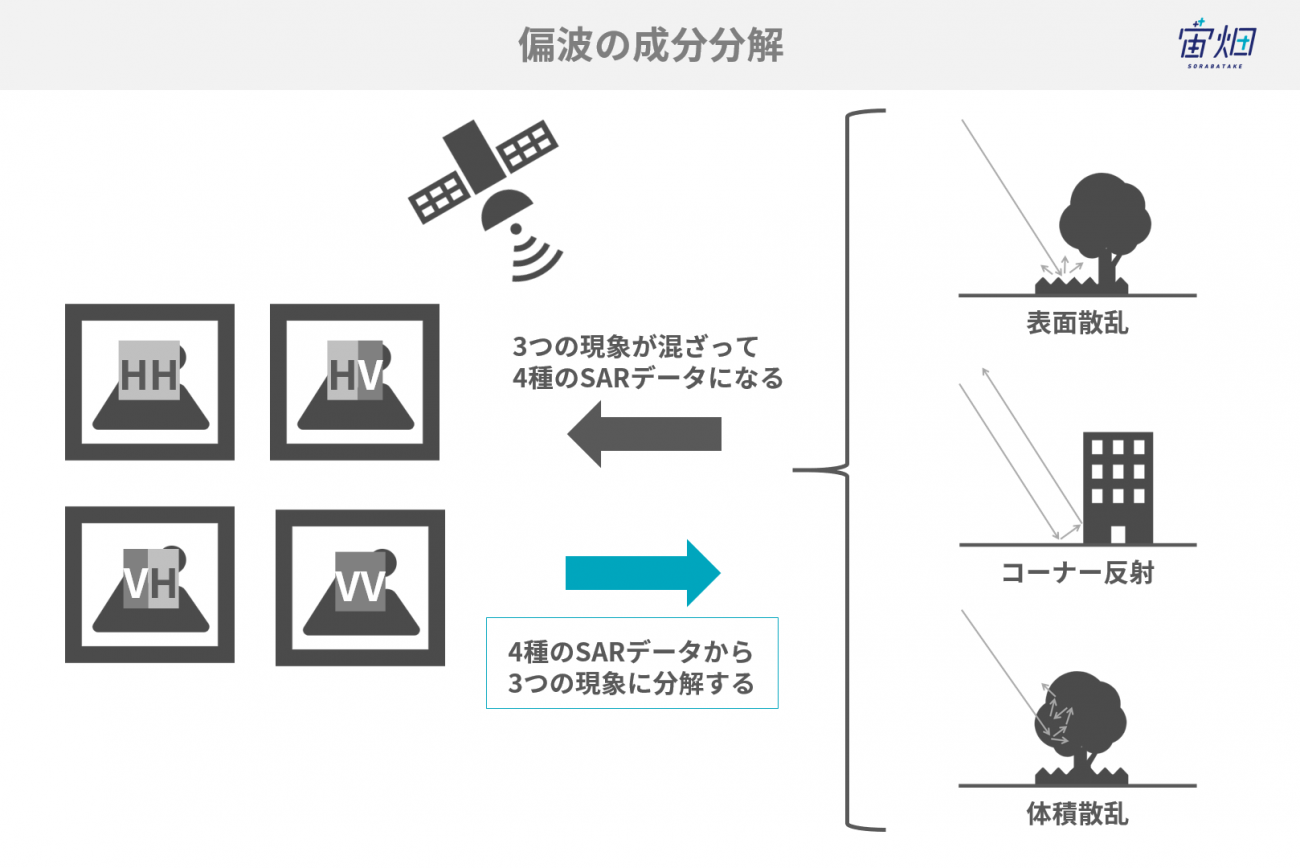
散乱プロセス（表面散乱、コーナー反射、体積散乱）によって、偏波のどの成分に寄与するかが異なるため、フルポラリメトリ(4偏波)揃ったSAR画像から、散乱プロセスを「1回反射（表面散乱）、2回反射、体積散乱」の3つに分類することができます。これを「偏波の成分分解」と言います。

フルポラリメトリのCEOSを取得

偏波の成分分解を行うにあたって4偏波のデータ必要です。以下の記事等を参考にフルポラリメトリのデータを取得していきたいと思います。

import os, requests
import geocoder # ! pip install geocoder

# Fields
BASE_API_URL = "https://file.tellusxdp.com/api/v1/origin/search/" # https://www.tellusxdp.com/docs/api-reference/palsar2-files-v1.html#/
ACCESS_TOKEN = "YOUR_TOKEN"
HEADERS = {"Authorization": "Bearer " + ACCESS_TOKEN}
TARGET_PLACE="kasumigaura, ibaraki"
SAVE_DIRECTORY="./data/"

# Functions
def rect_vs_point(ax, ay, aw, ah, bx, by):
    return 1 if bx > ax and bx < aw and by > ay and by < ah else 0
def get_scene_list_slc(_get_params={}):
    query = "palsar2-l11"
    r = requests.get(BASE_API_URL + query, _get_params, headers=HEADERS)
    if not r.status_code == requests.codes.ok:
        r.raise_for_status()
    return r.json()

def get_slc_scenes(_target_json, _get_params={}):
    # get file list
    r = requests.get(_target_json["publish_link"], _get_params, headers=HEADERS)
    if not r.status_code == requests.codes.ok:
        r.raise_for_status()
    file_list = r.json()['files']
    dataset_id = _target_json['dataset_id'] # folder name
    # make dir
    if os.path.exists(SAVE_DIRECTORY + dataset_id) == False:
        os.makedirs(SAVE_DIRECTORY + dataset_id)
    # downloading
    print("[Start downloading]", dataset_id)
    for _tmp in file_list:
        r = requests.get(_tmp['url'], headers=HEADERS, stream=True)
        if not r.status_code == requests.codes.ok:
            r.raise_for_status()
        with open(os.path.join(SAVE_DIRECTORY, dataset_id, _tmp['file_name']), "wb") as f:
            f.write(r.content)
        print("  - [Done]", _tmp['file_name'])
    print("finished") 
    return

# Entry point
def main():
    # extract slc list around the address
    gc = geocoder.osm(TARGET_PLACE, timeout=5.0) # get latlon
    slc_list_json = get_scene_list_slc({'after':'2019-1-01T00:00:00', 'polarisations':'HH+HV+VV+VH', 'page_size':'1000'})  # get single look complex list
    target_places_json = [_ for _ in slc_list_json['items'] if rect_vs_point(_['bbox'][1], _['bbox'][0], _['bbox'][3], _['bbox'][2], gc.latlng[0], gc.latlng[1])] # lot_min, lat_min, lot_max...
    target_ids = [_['dataset_id'] for _ in target_places_json]
    print("[Matched SLCs]", target_ids)
    for target_id in target_ids:
        target_json = [_ for _ in slc_list_json['items'] if _['dataset_id'] == target_id][0]
        # download the target file
        get_slc_scenes(target_json)
        break # if remove, download all data
    
if __name__=="__main__":
       main()

このソースコードは条件に合うSAR L1.1をリスト化しダウンロードしてくるプログラムです。リスト全てをダウンロードすると、すぐにHDDが埋まってしまうので最後の方に”break”を挿入してあります。これにより、リストの最初だけダウンロードしてくる仕組みになっています。

main関数内のコードを説明します。

始めに以下でTARGET_PLACEという住所の緯度と経度を取得しています。

 gc = geocoder.osm(TARGET_PLACE, timeout=5.0) #get latlon

これはgeocoderというライブラリを使うため、以下でライブラリを導入しましょう。

一々、緯度経度を調べる必要がなくなるので便利です。

次に、以下でフルポラリメトリ(HH、HV、VV、VH)のデータリストを得ています。

slc_list_json = get_scene_list_slc({'after':'2019-1-01T00:00:00', 'polarisations':'HH+HV+VV+VH', 'page_size':'1000'})

続いて以下の2行でgeocoderから得た緯度経度にマッチするSAR画像のリストを作成します。

    target_places_json = [_ for _ in slc_list_json['items'] if rect_vs_point(_['bbox'][1], _['bbox'][0], _['bbox'][3], _['bbox'][2], gc.latlng[0], gc.latlng[1])]
    target_ids = [_['dataset_id'] for _ in target_places_json]

これにより条件に合ったSAR画像のリストが”target_ids”に保存されるため、これを参照してダウンロードを開始していきます。今回は” ALOS2249732860-190107”のみをダウンロードします。ダウンロードが完了すると”./data/ALOS2249732860-190107”のフォルダ下にフルポラリメトリのSARデータが保存されています。

フルポラリメトリCEOSをパースする

CEOSの状態ではヘッダ情報とペイロード等が1つになってしまい、各データを分離できていません。ペイロード部分も複素データになっており虚部と実部で分かれていません。そこで、CEOSからペイロード部分を抽出すると伴に、複素データを分割します。この分析、抽出、分割することをパースといいます。

始めに”slcinfo.py”というSAR L1.1をパースするクラスを作成します。

class SLC_L11:
    def __init__(self, _file_name):
        self.file_name = _file_name
        self.fp = 0
        self.width = 0
        self.height = 0
        self.level = 0
        self.format = ""
        self.data = []
        
    def get_width(self):
        self.fp.seek(248)
        self.width = int(self.fp.read(8))

    def get_height(self):
        self.fp.seek(236)
        self.height = int(self.fp.read(8))
    
    def get_level(self):
        self.fp.seek(276) # if l1.1, return "544"
        self.level = int(self.fp.read(4))
   
    def get_format(self):
        self.fp.seek(400)
        self.format = self.fp.read(28).decode()
        
    def get_data(self):
        self.fp.seek(720)
        prefix_byte = 544
        data = np.zeros((self.height, self.width, 2))
        width_byte_length = prefix_byte + self.width*8 # prefix + width * byte (i32bit + q32bit)
        for i in tqdm(range(self.height)):
            data_line = struct.unpack(">%s"%(int((width_byte_length)/4))+"f", self.fp.read(int(width_byte_length)))
            data_line = np.asarray(data_line).reshape(1, -1)
            data_line = data_line[:, int(prefix_byte/4):] # float_byte:
            slc = data_line[:,::2] + 1j*data_line[:,1::2]
            data[i, :, 0] = slc.real
            data[i, :, 1] = slc.imag
        # multiplex
        self.data = data[:, :, 0] + 1j*data[:, :, 1]
        print("done")
        
    def parse(self):
        self.fp = open(self.file_name, mode='rb')   
        self.get_width()
        self.get_height()
        self.get_level()
        self.get_format()
        self.get_data()
        self.fp.close()
        self.fp = 0

“parse()”関数を実行するとCEOSファイルから画像サイズや内部の複素データを取り出す仕組みです。複素データを取り出す部分は”get_data()”関数に記述されています。画像サイズ分、ラインごとに各複素データを取り出しています。

このクラスは以下のように使います。

import os
import struct
import numpy as np
import glob
import pickle
import gc
from slcinfo import SLC_L11

# Fields
SAVE_DIRECTORY="./data/"

# Entry point
def main():   
    product_list = os.listdir(SAVE_DIRECTORY)
    for product_name in product_list:
        slc_list = glob.glob(SAVE_DIRECTORY + product_name + "/IMG-*_D")
        for slc_name in slc_list:
            print(slc_name)
            slc = SLC_L11(slc_name)
            slc.parse()
            slc.crop_data(3000, 8000, 2000) # if you use cropping,
            with open(slc_name + ".pkl", "wb") as f:
                pickle.dump(slc, f)
            slc = None
            gc.collect()

if __name__=="__main__":
       main()

これを実行すると先ほどダウンロードしたフルポラリメトリのデータ分だけ、パース処理が行われます。処理が完了すると、フルポラリメトリのデータと同じファイル名の後に”pkl”という拡張子が付き、パース済みデータが保存されます。

こちらのソースコードについて簡単に説明します。

まず、以下で各偏波のCEOSデータのファイル場所を取得しています。

slc_list = glob.glob(SAVE_DIRECTORY + product_name + "/IMG-*_D")

次に、以下の二行でCEOSデータをパースしています。

  slc = SLC_L11(slc_name)
            slc.parse()

CEOSデータを1枚まるごと保存すると非常に容量を食ってしまうので以下で切り取っています。

            slc.crop_data(3000, 8000, 2000) # if you use cropping,

切り取り後、以下で保存しています。

       with open(slc_name + ".pkl", "wb") as f:
                pickle.dump(slc, f)

保存終了後、次のCEOSデータを読み込むのですが、その際にメモリ不足にならないように、これまで確保したメモリを解放します。

            slc = None
            gc.collect()

ここまで終了すると以下のデータが得られているはずです。

IMG-HH-ALOS2249732860-190107-HBQL1.1__D
IMG-HH-ALOS2249732860-190107-HBQL1.1__D.pkl
IMG-HV-ALOS2249732860-190107-HBQL1.1__D
IMG-HV-ALOS2249732860-190107-HBQL1.1__D.pkl
IMG-VV-ALOS2249732860-190107-HBQL1.1__D
IMG-VV-ALOS2249732860-190107-HBQL1.1__D.pkl
IMG-VH-ALOS2249732860-190107-HBQL1.1__D
IMG-VH-ALOS2249732860-190107-HBQL1.1__D.pkl

偏波の成分分解 (Polarimetric Decomposition)によるレーダ反射回数の取得

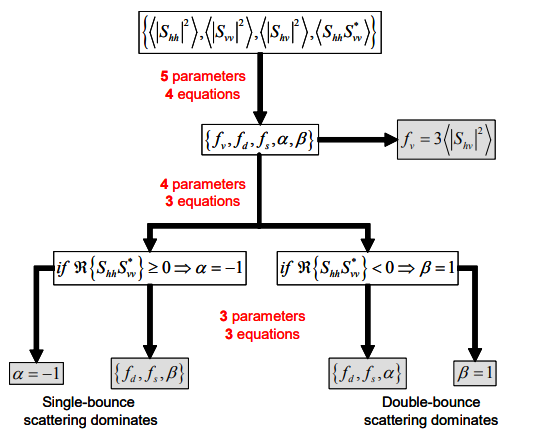
偏波の成分分解の方法は、対象物の仮定の仕方によって大きく分けて2種類あります。

「Coherent Decomposition（コヒーレントデコンポジション）」と「Incoherent Decomposition（インコヒーレントデコンポジション）」です。

・Coherent Decomposition（コヒーレントデコンポジション）：

この方法はノイズが発生しない理想的な表面から得られる散乱を仮定してSAR画像の解析を行う手法です。代表的な手法には「Pauli Decomposition」があります。

ただし、レーダはその仕組み上、熱雑音等によりスペックルノイズと呼ばれるSAR特有のノイズが発生してしまうため、実際には本仮定とはずれているということになります。そこで考えられたのが次の手法です。。

・Incoherent Decomposition（インコヒーレントデコンポジション）：

こちらの方法は、Coherent Decompositionで無視したノイズの影響を考慮したアプローチです。

偏波の成分分解をする前に、統計的処理で前述のスペックルノイズを低減させる処理を行ってます。このため、ノイズの多いレーダの装置と相性が良いと言われています。

代表的な手法には「Freeman Duran Decomposition」があります。

今回は、それぞれに代表される手法を実装して、比較してみることにしました。

Pauli Decomposition(Coherent Decomposition)

こちらは次式によって分解することができます。

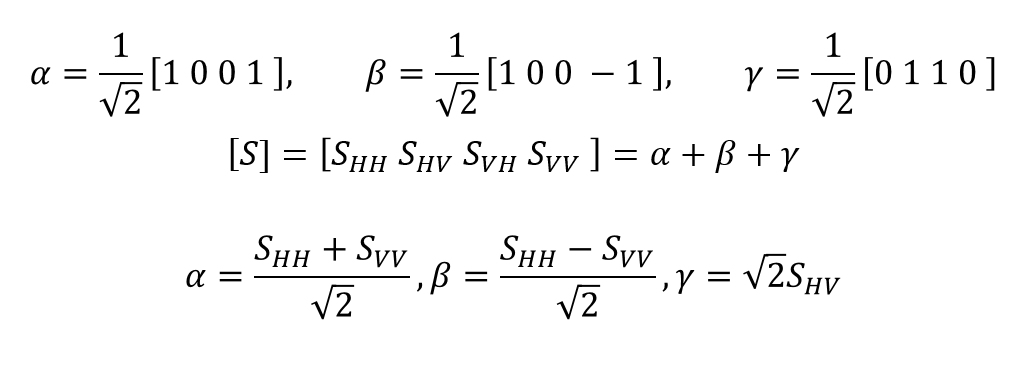
ここで、S_HV=S_VHとし、各成分は1回反射、2回反射、体積散乱とします。また、慣用的に[α,β,ɤ]=[s,d,v]=[B,R,G]のように色をマッピングします。

こちらを実装したコードは以下の通りです。

%matplotlib inline
import os
import struct
import numpy as np
import glob
from tqdm import tqdm
import pickle
import cv2
import matplotlib.pyplot as plt
from slcinfo import SLC_L11
import gc

# Fields
SAVE_DIRECTORY="./data/"

def get_intensity(_slc): 
    return 20*np.log10(abs(_slc)) - 83.0 - 32.0

def normalization(_x):
    return (_x-np.amin(_x))/(np.amax(_x)-np.amin(_x))

def adjust_value(_x):
    _x = np.asarray(normalization(_x)*255, dtype="uint8")
    return cv2.equalizeHist(_x)

def slc2pauli(_hh, _hv, _vv, _vh, _cross=0):
    if _cross == 0:
        _cross = (_hv + _vh) / 2
    else:
        _cross = _hv    
    single = ((_hh+_vv)/np.sqrt(2)) # single, odd-bounce.
    double = ((_hh-_vv)/np.sqrt(2)) # double, even-bounce
    vol = np.sqrt(2)*_cross # vol
    return np.asarray([single, double, vol])

def grayplot(_file_name, _v):
    plt.figure()
    plt.imshow(_v, cmap = "gray")
    plt.imsave(_file_name, _v, cmap = "gray")
    print("[Save]", _file_name)
    
def rgbplot(_file_name, _alpha_r, _gamma_g, _beta_b):
    plttot=(np.dstack([_alpha_r, _gamma_g,_beta_b]))
    plttot=np.asarray(plttot, dtype="uint8")
    plt.figure()
    plt.imshow(plttot)
    plt.imsave(_file_name, plttot)
    print("[Save]", _file_name)
    return

# Entry point
def main():
    offset_x = 3000
    offset_y = 8000
    limit_length = 2000
    slc_hh = 0
    slc_hv = 0
    slc_vv = 0
    slc_vh = 0
    product_list = os.listdir(SAVE_DIRECTORY)
    for product_name in product_list:
        slc_list = glob.glob(SAVE_DIRECTORY + product_name + "/IMG-*.pkl")
        for slc_name in slc_list:
            with open(slc_name, "rb") as f:
                slc = pickle.load(f)
            if "IMG-HV" in slc_name:
                slc_hv = slc.data
            if "IMG-HH" in slc_name:
                slc_hh = slc.data
            if "IMG-VV" in slc_name:
                slc_vv = slc.data
            if "IMG-VH" in slc_name:
                slc_vh = slc.data
            slc_tmp = slc2intensity(slc.data)
            grayplot(slc_name + "_p.png", adjust_value(slc_tmp))
            slc = None
            gc.collect()
        
        ##################################
        # pauli
        ##################################
        result = slc2pauli(_hh=slc_hh, _hv=slc_hv, _vv=slc_vv, _vh=slc_vh) # alpha, beta, gmma
        [s, d, v] = get_intensity(result)
        rgbplot(SAVE_DIRECTORY + product_name + "/Pauli_decomposition.png", _alpha_r=adjust_value(d), _gamma_g=adjust_value(v), _beta_b=adjust_value(s))
        
if __name__=="__main__":
       main()

これを実行すると以下のような結果が得られます。

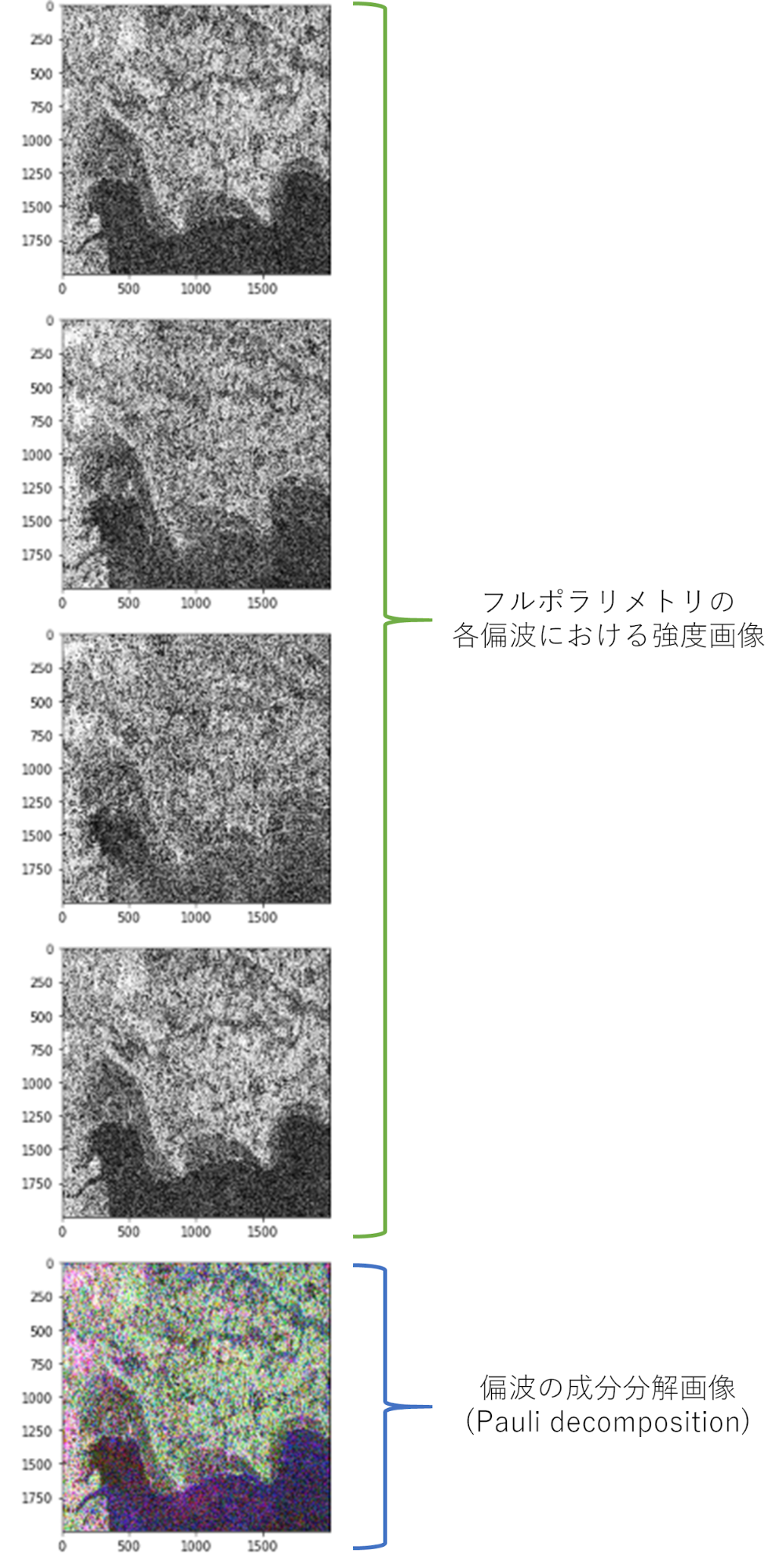
各偏波の強度画像の後に偏波の成分分解した画像が表示されます。
また、これらの画像は読み込み元のフルポラリメトリのフォルダに保存されます。

それでは簡単にコードの説明をします。

まず、以下からフルポラリメトリのファイル一覧を読み込みしています。

   slc_list = glob.glob(SAVE_DIRECTORY + product_name + "/IMG-*.pkl")

次に、以下でフルポラリメトリの各偏波成分をロードしています。

 for slc_name in slc_list:
            with open(slc_name, "rb") as f:
                slc = pickle.load(f)
            if "IMG-HV" in slc_name:
                slc_hv = slc.data
            if "IMG-HH" in slc_name:
                slc_hh = slc.data
            if "IMG-VV" in slc_name:
                slc_vv = slc.data
            if "IMG-VH" in slc_name:
                slc_vh = slc.data
            slc_tmp = slc2intensity(slc.data)
            grayplot(slc_name + "_p.png", adjust_value(slc_tmp))
            slc = None
            gc.collect()

最後に以下のコードでフルポラリメトリのデータを偏波の成分分解した後に強度変換を行っています。

    result = slc2pauli(_hh=slc_hh, _hv=slc_hv, _vv=slc_vv, _vh=slc_vh) # alpha, beta, gmma
        [s, d, v] = get_intensity(result)
        rgbplot(SAVE_DIRECTORY + product_name + "/Pauli_decomposition.png", _alpha_r=adjust_value(d), _gamma_g=adjust_value(v), _beta_b=adjust_value(s))

偏波の成分分解は具体的に以下の関数によって行われています。

def slc2pauli(_hh, _hv, _vv, _vh, _cross=0):
    if _cross == 0:
        _cross = (_hv + _vh) / 2
    else:
        _cross = _hv    
    single = ((_hh+_vv)/np.sqrt(2)) # single, odd-bounce.
    double = ((_hh-_vv)/np.sqrt(2)) # double, even-bounce
    vol = np.sqrt(2)*_cross # vol
    return np.asarray([single, double, vol])

_cross引数の部分について説明します。これはクロス偏波の計算方法を指定する引数です。支配方程式上でHV=VHの関係であることを説明しましたが、実際はノイズ等により同じものになることは少ないです。そこで、安定化のために平均を取ってクロス偏波とするような仕組みを用意しています。

変換結果が正しいか、専門のソフトウェアで変換した結果と比較してみます。

今回のコード:

専門のソフトウェア:

2つの画像にほとんど差異はなく、上手く変換できたといえます。

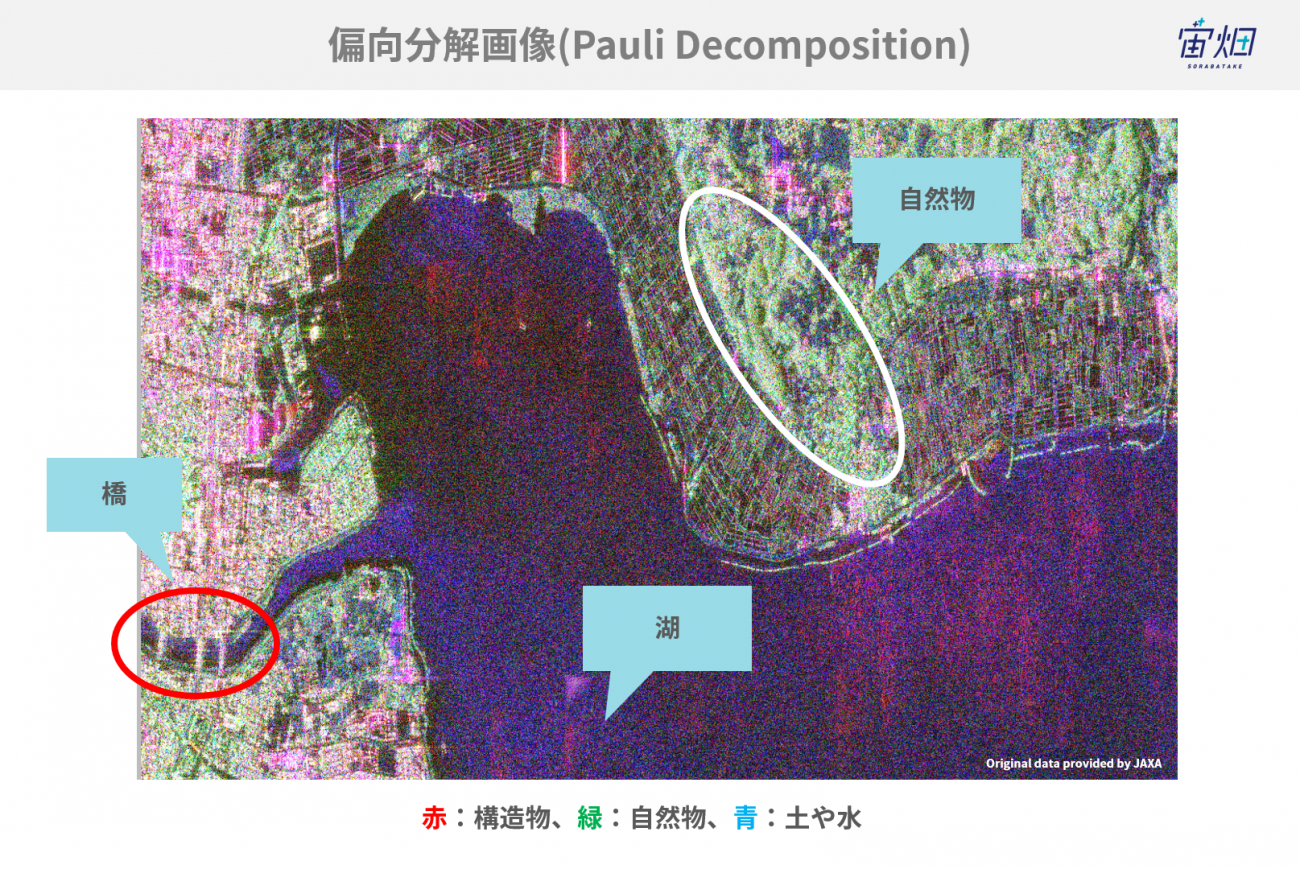
また、当初の目的である「土地被覆分類や物体識別」について、見てみると、橋などの構造物が赤く(2回反射)、海は青く(1回反射)、土や木は緑(体積散乱)となっていることが確認できました。

Freeman Duran Decomposition(Incoherent Decomposition)

こちらは一度、統計的処理で前述のスペックルノイズを低減させる処理を行った後に偏波の成分分解を行います。また、偏波の成分分解もPauli Decompositionのように単純ではなく、以下のような条件分岐があります。詳細な説明は非常に長くなるため、今回は割愛します。興味がある方は、元の資料を読んでみてください。

こちらの実装コードは以下の関数です。
※先ほどのPauli Decompositionのソースコードに追加する形で使用してください。

def slc2cov(_hh, _hv, _vv, _vh, _nb=2, _cross=0):    
    [m,n] = _hh.shape
    result = np.zeros((m,n,9),dtype=np.complex64)
    if _cross == 0:
        _cross = (_hv + _vh) / 2
    else:
        _cross = _hv   
    cross = cross * np.sqrt(2)
    for i in tqdm(np.arange(0, m)):
        for j in np.arange(0, n):
            
            i_one = np.array((0, i - _nb))
            i_two = np.array((i+_nb+1, m))
            
            j_one = np.array((0, j-_nb))
            j_two = np.array((j+_nb + 1, n))
    
            hh_tmp = np.copy(_hh[np.max(i_one):np.min(i_two),np.max(j_one):np.min(j_two)])
            vv_tmp = np.copy(_vv[np.max(i_one):np.min(i_two),np.max(j_one):np.min(j_two)])
            cross_tmp = np.copy(cross[np.max(i_one):np.min(i_two),np.max(j_one):np.min(j_two)])

            [mbis,nbis]=hh_tmp.shape
            
            hh_tmp = hh_tmp.reshape((mbis*nbis, 1))
            vv_tmp = vv_tmp.reshape((mbis*nbis, 1))
            cross_tmp = cross_tmp.reshape((mbis*nbis, 1))

            data = np.hstack((hh_tmp, cross_tmp, vv_tmp))
            
            cov = np.dot(data.T,np.conjugate(data))/(mbis*nbis)
            result[i,j,:] = cov.reshape(9,)   
    return result

def cov2fdd(data):
    [m, n, p] = data.shape
    pv_array = np.zeros((m, n))
    pd_array = np.zeros((m, n))
    ps_array = np.zeros((m, n))    
    for i in tqdm(np.arange(0, m)):
        for j in np.arange(0, n):        
            cov=(np.copy(data[i,j,:])).reshape((3, 3))
            fv=(3*cov[1,1]/2).real            
            if (cov[0,2]).real<=0:
                beta=1
                
                Af=(cov[0,0]-fv).real
                Bf=(cov[2,2]-fv).real
                Cf=((cov[0,2]).real-fv/3).real
                Df=(cov[0,2]).imag
                
                if (Af+Bf-2*Cf)!=0:
                    fd=(Df**2+(Cf-Bf)**2)/(Af+Bf-2*Cf)
                else:
                    fd=Bf
                
                fs=Bf-fd
                
                if fd!=0:
                    alpha=np.complex((Cf-Bf)/fd+1, Df/fd)
                else:
                    alpha=np.complex(1,1)
                
            else:           
                alpha=-1
                
                Af=(cov[0,0]-fv).real
                Bf=(cov[2,2]-fv).real
                Cf=(cov[0,2]).real-fv/3
                
                if (Af+Bf+2*Cf)!=0:                    
                    fs=(Cf+Bf)**2/(Af+Bf+2*Cf)
                else:
                    fs=Bf
                    
                fd=Bf-fs
                beta=(Af+Cf)/(Cf+Bf)       
                
            pv=(8*fv/3)
            ps=(fs*(1+beta*np.conjugate(beta))).real
            pd=(fd*(1+alpha*np.conjugate(alpha))).real
            
            ps_array[i, j] = ps
            pd_array[i, j] = pd
            pv_array[i, j] = pv
    return np.asarray([ps_array, pd_array, pv_array])

使い方は、main関数から以下のように呼んでください。

        ##################################
        # freeman-duran
        ##################################
        # convert slc to cov
        cov_file_name = SAVE_DIRECTORY + product_name + "/cov.pkl" 
        if not os.path.exists(cov_file_name):
            cov = slc2cov(slc_hh, slc_vv, slc_vv, slc_vh, 2)
            with open(cov_file_name, "wb") as f:
                pickle.dump(cov, f)
        with open(cov_file_name, "rb") as f:
            cov = pickle.load(f)

        # convert freeman-duran
        freeman_file_name = SAVE_DIRECTORY + product_name + "/fdd.pkl" 
        if not os.path.exists(freeman_file_name):
            fdd = cov2fdd(cov)
            with open(freeman_file_name, "wb") as f:
                pickle.dump(fdd, f)
        with open(freeman_file_name, "rb") as f:
            fdd = pickle.load(f)
        [s, d, v] = get_intensity(fdd)
        rgbplot(SAVE_DIRECTORY + product_name + "/Freeman_decomposition.png", _alpha_r=adjust_value(d), _gamma_g=adjust_value(v), _beta_b=adjust_value(s))

処理が終わるとこのように偏波の成分分解された画像が表示されます。

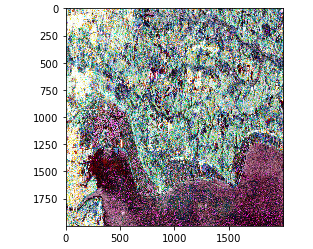
それでは専門のソフトウェアと比較してみましょう。

今回のコード:

専門のソフトウェア:

RGB化の方法が異なるのか完全一致とまではいきませんでしたが、傾向はかなり似ていますね。

まとめ

当初の目的が達成できたかの確認とこれまでのまとめをしたいと思います。

まずは、当初の目的を再掲します。
「今回の記事では、この偏波の成分分解をPALSAR-2のSAR L1.1に対して行い、実際に構造物と自然物を選り分けることが出来るのかを確認していきたいと思います。」

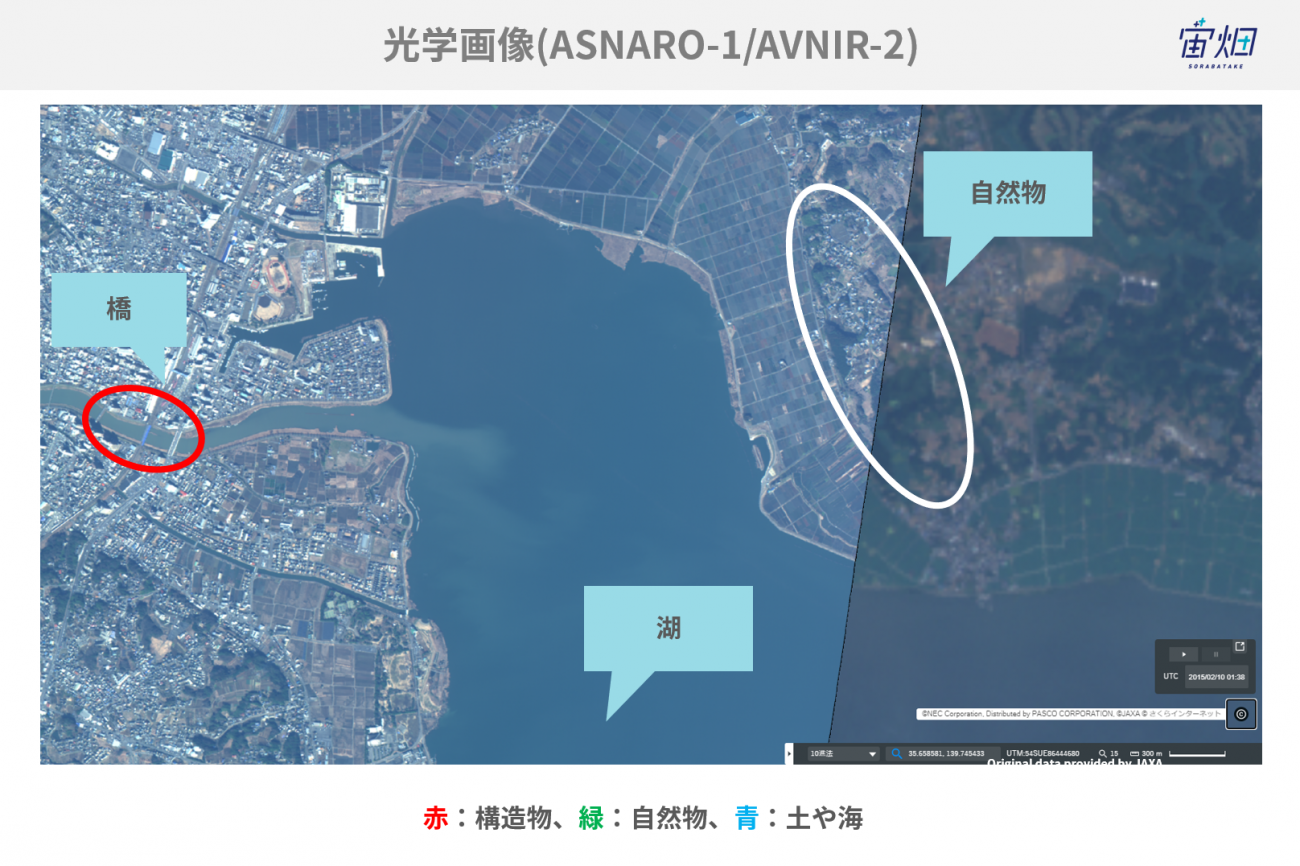
では、この目的が達成できたのかということで、光学画像とSARの偏波の成分分解画像を比較したいと思います。

光学画像:

偏波の成分分解(Pauli decomposition):

偏波の成分分解(Freeman-duran):

Freeman-duranはややノイズが多く乗ってしまっていますが、構造物と自然物(土、山、木)の見分けはある程度出来ているのではないかなと思います。
ということで、今回は目的を達成することが出来たということになります。

では最後に、今回行ったことを振り返ってまとめとしたいと思います。

・SARの散乱プロセス（1回反射、2回反射、体積散乱）について学んだ
・フルポラリメトリを偏波の成分分解することで「1回反射、2回反射、体積散乱」の情報を得られることが分かった
・偏波の成分分解から簡易的な物体識別ができることを学んだ
・フルポラリメトリCEOS (SAR L1.1)からデータを取得し、2手法で偏波の成分分解を行った
・偏波の成分分解の結果を専門のソフトウェアと比較することで適切に動作していることを確認した
・偏波分解の結果と光学画像を比較した結果、構造物と自然物をある程度選り分けることができるのを確認した

また、冒頭でも説明しましたが、この処理は構造物と自然物を選り分けるだけでなく、SAR画像を扱いやすくするための処理だとも考えられます。

SAR画像を扱いやすくするための処理は、ノイズを除去するなど余計なものを削除するものは数多くありますが、今回のアプローチは画像全体に新しい情報を付加することができるので、画像の前処理として非常に有効です。

今後、宙畑の記事では本内容の発展的な内容についても扱っていきたいと思いますので、お楽しみに！