記事作成時から、Tellusからデータを検索・取得するAPIが変更になっております。該当箇所のコードについては、以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/access/traveler_api_20220310_
firstpart.html

2022年8月31日以降、Tellus OSでのデータの閲覧方法など使い方が一部変更になっております。新しいTellus OSの基本操作は以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/tellus_os/start_tellus_os.html

以前、富士山が見える場所を計算しようという記事を公開しました。

こちらの記事ついて、多数のご指摘をいただきましたので、改めて「地球の丸さ」を考慮して解析を行いました。アドバイスをいただいた皆様には改めて御礼申し上げます。

2地点間の可視性の考え方

可視性を考える際に、考えなければいけないポイントが二つあります。
一つは地球の丸さを考慮することで、もう一つが光の屈折を考慮することです。
厳密には他にもいろいろとあると思いますが、今回はこの2点を考慮したいと思います。

(1) 地球の丸さ

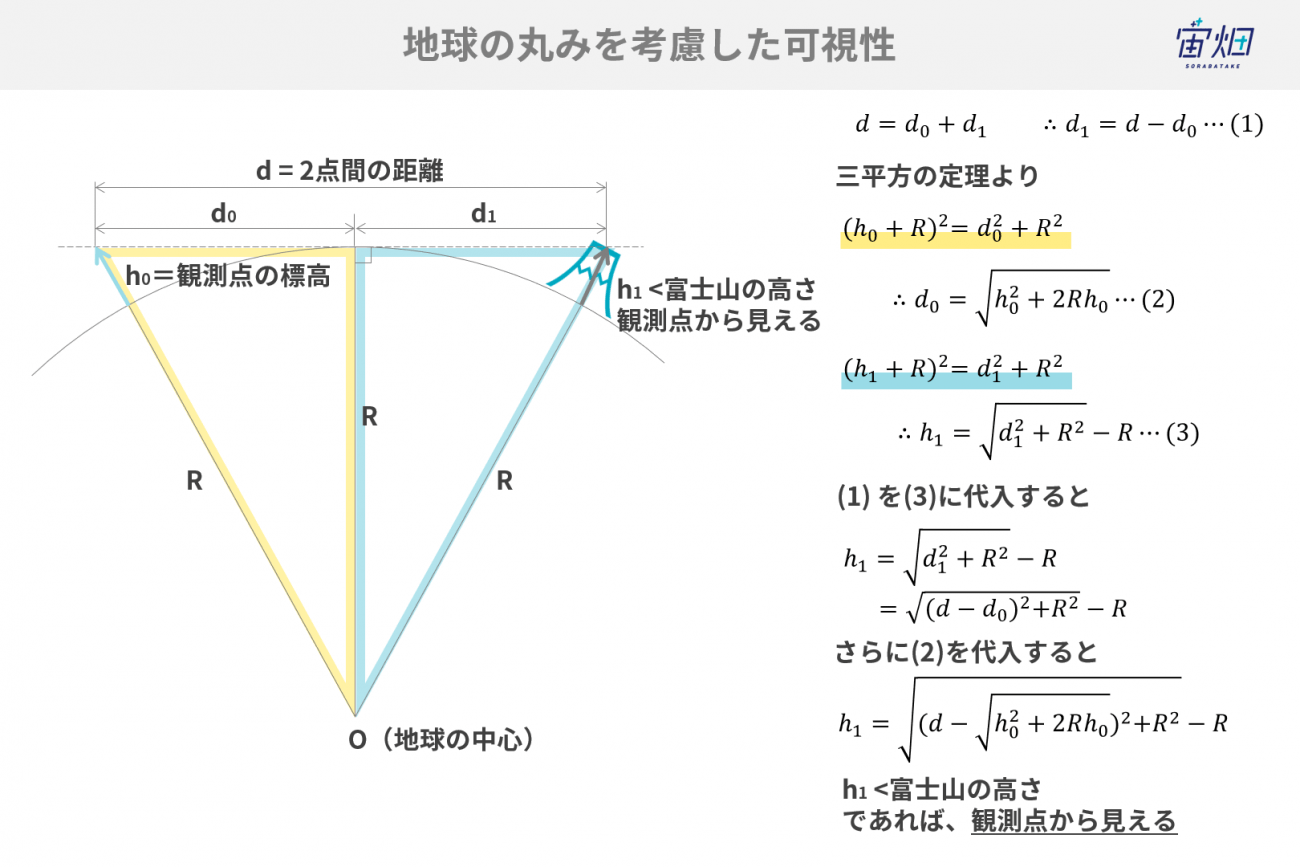
地面が平面とみなせる程度に狭い範囲であれば、前回の記事で説明した方法で解析を実施すれば良いのですが、実際には地球は球体でありその丸さを考慮する必要があります。

上図のように、平面であれば見えているはずでも、地球が丸いために富士山自体が沈み込み、地平線に隠れてしまう可能性があります。

そこで、観測点の標高（h0）と2点間の距離から、水平線ギリギリで見える高さ（h1）を算出し、h1が富士山の標高よりも低ければ「富士山が見える」、h1が富士山の標高よりも高ければ「富士山は見えない」という整理にしました。

(2)光の屈折

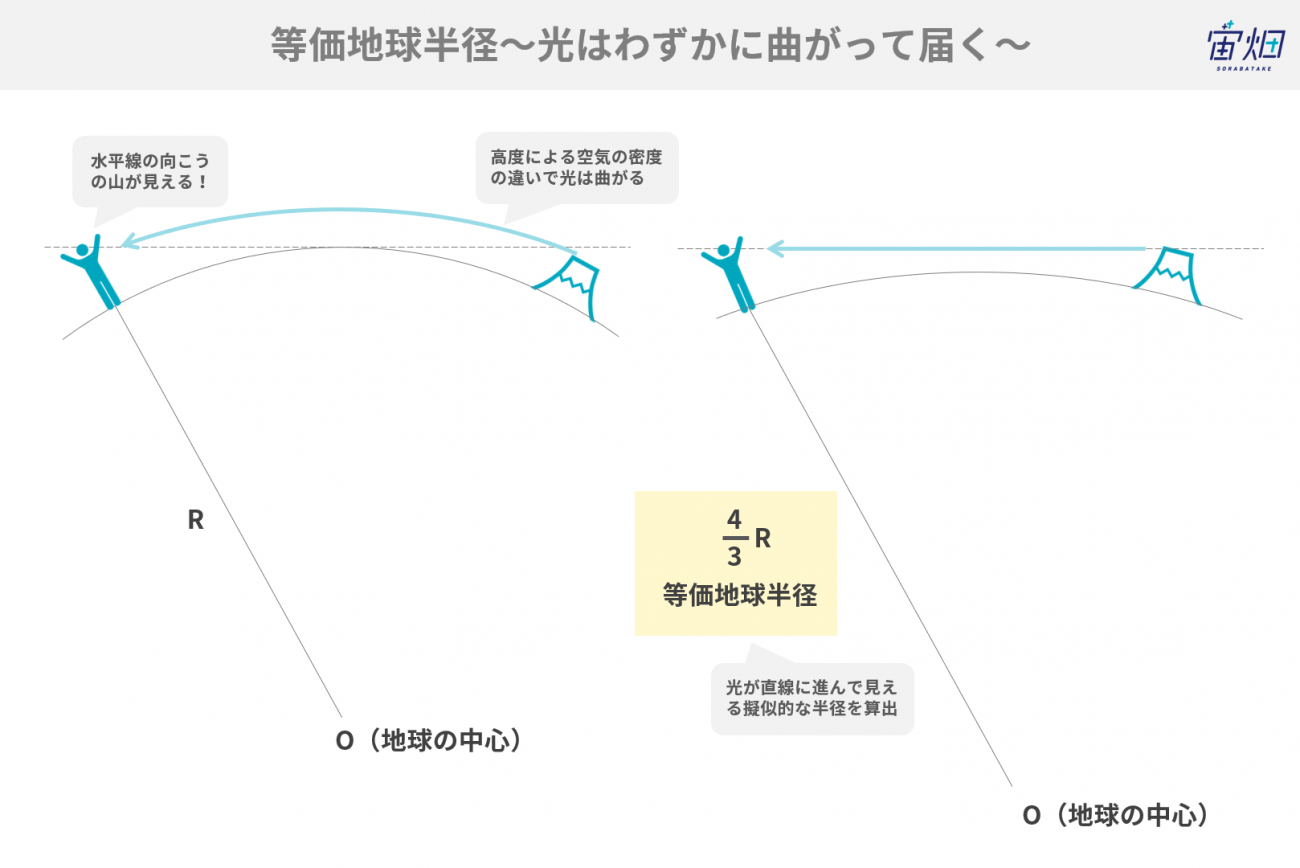
もう一つ考慮したいのが「光の屈折」です。

空気は高度が上がれば上がるほど薄くなります。

光は密度の異なる媒質の中を進むとき、密度の高い側に寄るように屈折する性質があるため、(1)の計算では見えないはずのものが少しだけ見えるという現象がおきます。

この光の屈折による効果は、光がまっすぐに進むとした場合に、同じように見える擬似的な半径を仮定することで算出できます。この半径を「等価地球半径」と呼び、実際の地球の半径の4/3倍とすれば良いことが知られています。

※本記事では可視光と電磁波の屈折率を同一とみなして計算しています。厳密な結果を求める場合は、適時コードを修正してご使用ください。

参考
無線工学の基礎
http://www.gxk.jp/elec/musen/1ama/H13/html/H1312B05_.html

コード実行手順

上記の地球の丸さと光の屈折を考慮に入れコードを修正しました。（文末にコード全文を掲載しています。）ここではこのコードを使い、任意の地点と富士山の可視性を確認する手順を紹介します。

1.Tellusの開発環境を申請し、APIキーを入手します。詳細は下の記事をご参考ください。
https://sorabatake.jp/5048/

2.コード中の TOKEN = ‘YOUR-API-KEY’をご自身のAPIキーに起きかえます。

3.次に raw1=[] に、富士山との見通しを確認したい任意の地点の緯度経度を、指定して下さい。サンプルとしていくつかの地点を記入してあります。こちらをコメントアウトしても使えます。

4.実行すると2地点の見通しを判定します。

#----------【設定箇所】----------#

#ご自身のAPIキーを設定してください
#参考：https://sorabatake.jp/5048
TOKEN = 'YOUR-API-KEY'

#地球の半径(km)
earth_r = 8490; #理想大気 （実際の半径は6371km）

# 見通しを判定したい任意の地点を緯度経度で指定
#例
# raw1 = [33.471744, 135.860882] #樫野埼灯台 （串本町　潮岬 見通し不可）
raw1 = [33.693889, 135.848611] #色川富士見峠 （那智勝浦町 最遠望）

#富士山
raw2 = [35.360833, 138.727500] #富士山 3776m

z=12 #zoomレベル設定
#--------------------------------#

結果を以下のように出力します。

青く見えている画像が、標高タイル（ASTER GDEM 2.0）です。

その下が、2点間の標高のグラフです。

最後に見通しの結果を出力します。

例：
色川富士見峠 （那智勝浦町  最遠望）

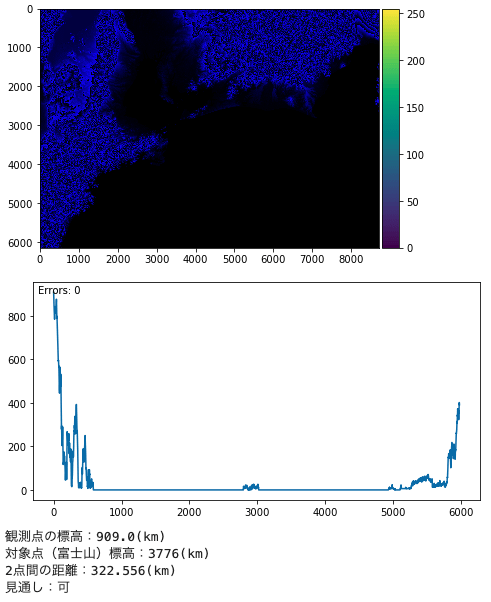
例：
樫野埼灯台（串本町 潮岬）

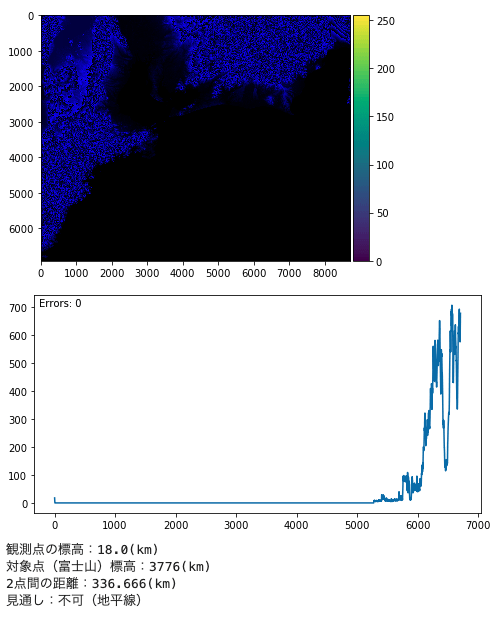
ぜひ、みなさんも自分の住んでいる場所などを、設定して試してみてください。

【コード全文】

import requests, json
import numpy
from numpy import arctanh
from skimage import io
from io import BytesIO
import math
from math import *
import matplotlib.pyplot as plt
%matplotlib inline

def vincenty_inverse(lat1, lon1, lat2, lon2, ellipsoid=None):
    """
    緯度経度で指定した2地点間の距離を返す
    """
    # 楕円体
    ELLIPSOID_GRS80 = 1 # GRS80
    ELLIPSOID_WGS84 = 2 # WGS84

    # 楕円体ごとの長軸半径と扁平率
    GEODETIC_DATUM = {
        ELLIPSOID_GRS80: [
            6378137.0,         # [GRS80]長軸半径
            1 / 298.257222101, # [GRS80]扁平率
        ],
        ELLIPSOID_WGS84: [
            6378137.0,         # [WGS84]長軸半径
            1 / 298.257223563, # [WGS84]扁平率
        ],
    }

    # 反復計算の上限回数
    ITERATION_LIMIT = 1000

    # 差異が無ければ0.0を返す
    if isclose(lat1, lat2) and isclose(lon1, lon2):
        return 0.0

    # 計算時に必要な長軸半径(a)と扁平率(ƒ)を定数から取得し、短軸半径(b)を算出する
    # 楕円体が未指定の場合はGRS80の値を用いる
    a, ƒ = GEODETIC_DATUM.get(ellipsoid, GEODETIC_DATUM.get(ELLIPSOID_GRS80))
    b = (1 - ƒ) * a

    φ1 = radians(lat1)
    φ2 = radians(lat2)
    λ1 = radians(lon1)
    λ2 = radians(lon2)

    # 更成緯度(補助球上の緯度)
    U1 = atan((1 - ƒ) * tan(φ1))
    U2 = atan((1 - ƒ) * tan(φ2))

    sinU1 = sin(U1)
    sinU2 = sin(U2)
    cosU1 = cos(U1)
    cosU2 = cos(U2)

    # 2点間の経度差
    L = λ2 - λ1

    # λをLで初期化
    λ = L

    # 以下の計算をλが収束するまで反復する
    # 地点によっては収束しないことがあり得るため、反復回数に上限を設ける
    for i in range(ITERATION_LIMIT):
        sinλ = sin(λ)
        cosλ = cos(λ)
        sinσ = sqrt((cosU2 * sinλ) ** 2 + (cosU1 * sinU2 - sinU1 * cosU2 * cosλ) ** 2)
        cosσ = sinU1 * sinU2 + cosU1 * cosU2 * cosλ
        σ = atan2(sinσ, cosσ)
        sinα = cosU1 * cosU2 * sinλ / sinσ
        cos2α = 1 - sinα ** 2
        cos2σm = cosσ - 2 * sinU1 * sinU2 / cos2α
        C = ƒ / 16 * cos2α * (4 + ƒ * (4 - 3 * cos2α))
        λʹ = λ
        λ = L + (1 - C) * ƒ * sinα * (σ + C * sinσ * (cos2σm + C * cosσ * (-1 + 2 * cos2σm ** 2)))

        # 偏差が.000000000001以下ならbreak
        if abs(λ - λʹ) <= 1e-12:
            break
    else:
        # 計算が収束しなかった場合はNoneを返す
        return None

    # λが所望の精度まで収束したら以下の計算を行う
    u2 = cos2α * (a ** 2 - b ** 2) / (b ** 2)
    A = 1 + u2 / 16384 * (4096 + u2 * (-768 + u2 * (320 - 175 * u2)))
    B = u2 / 1024 * (256 + u2 * (-128 + u2 * (74 - 47 * u2)))
    Δσ = B * sinσ * (cos2σm + B / 4 * (cosσ * (-1 + 2 * cos2σm ** 2) - B / 6 * cos2σm * (-3 + 4 * sinσ ** 2) * (-3 + 4 * cos2σm ** 2)))

    # 2点間の楕円体上の距離
    s = b * A * (σ - Δσ)

    # 各点における方位角
    α1 = atan2(cosU2 * sinλ, cosU1 * sinU2 - sinU1 * cosU2 * cosλ)
    α2 = atan2(cosU1 * sinλ, -sinU1 * cosU2 + cosU1 * sinU2 * cosλ) + pi

    if α1 < 0:
        α1 = α1 + pi * 2

    return s / 1000  #距離(km)

def get_combined_image(get_image_func, z, topleft_x, topleft_y, size=1):
    """
    指定した範囲のタイルを結合して取得
    """
    rows = []
    blank = numpy.zeros((256, 256, 4), dtype=numpy.uint8)
    
    for y in range(size):
        row = []
        for x in range(size):
            try:
                img = get_image_func(z, topleft_x + x, topleft_y + y)
            except Exception as e:
                img = blank
                
            row.append(img)
        rows.append(numpy.hstack(row))
    return  numpy.vstack(rows)


# 標高タイル（ASTER GDEM 2.0）を取得
def get_astergdem2_dsm(zoom, xtile, ytile):
    """
    ASTER GDEM2 の標高タイルを取得
    """
    url = " https://gisapi.tellusxdp.com/astergdem2/dsm/{}/{}/{}.png".format(zoom, xtile, ytile)
    headers = {
        "Authorization": "Bearer " + TOKEN
    }
    
    r = requests.get(url, headers=headers)
    return io.imread(BytesIO(r.content))

def latlon2tile2(lon, lat, z):
    """
    指定した緯度経度からピクセル座標を取得
    https://qiita.com/kobakou/items/4a5840542e74860a6b1b
    """
    L = 85.05112878
    x = int((lon/180 + 1) * 2**(z+7))
    y = int( (2**(z+7) / pi * ( -arctanh(sin(pi*lat/180)) + arctanh(sin(pi*L/180)) ) ))
    
    return [y, x]

def num2deg(xtile, ytile, zoom):
    """
    この関数は引数に ( x、y、z ) を指定することで、タイルの左上の角の緯度経度を返します。
    他にも、xとy の両方もしくは片方に、+1 した引数を指定すると別の角の座標を取得でき、
    +0.5 で中央の座標を取得できます。
    https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames#Python
    """
    n = 2.0 ** zoom
    lon_deg = xtile / n * 360.0 - 180.0
    lat_rad = atan(sinh(pi * (1 - 2 * ytile / n)))
    lat_deg = degrees(lat_rad)
    return (lon_deg, lat_deg)

def get_radian_btw_p1p2(y1, x1, y2, x2):
    """
    2点間のかたむき(y=ax)を取得する
    """
    #0で割ると division by zero エラーが出る
    if (x2 - x1) == 0:
        return "vertical"
    elif (y2 - y1) == 0:
        return "horizontal"
    else:
        return (y2 - y1) / (x2 - x1)

def get_heights_btw_p1p2(tile, y1, x1, y2, x2, radian):
    """
    始点から終点を結ぶ直線上の、標高データを取得
    一次関数：y = ax + b
    
    Parameters
    ----------
    tile : ndarray
        標高タイル
    y1 : number 
        点Aのy座標
    x1 : number 
        点AのX座標
    radian : number 
        傾き
    Returns
    -------
    actual_heights : ndarray
        x1y1を通り、かたむきradian上の標高データ
    """
    if radian == "vertical":
        return tile[:,y1]
    elif radian == "horizontal":
        return tile[x1,:]
    
    #原点を設定
    #x座標が小さい点をoriginに設定
    if x1 <= x2:
        origin_y = y1
        origin_x = x1
        point_y = y2
        point_x = x2
    else:
        origin_y = y2
        origin_x = x2
        point_y = y1
        point_x = x1
        
    max_index = len(tile) -1
    radian_tile = []
    
    while (round(origin_y) <= max_index and round(origin_x)  8388608:
        hyoko = (hyoko - 16777216)/u
    if hyoko < 8388608:
        hyoko = hyoko/u
    return hyoko

def plot_height(actual_heights, u=1):
    """
    高度のグラフをプロットする
    """
    heights = []
    heights_err = []

    for k in range(len(actual_heights)):
        R = actual_heights[k,0]
        G = actual_heights[k,1]
        B = actual_heights[k,2]
        try:
            heights.append(calc_height_chiriin_style(R, G, B, u))
        except ValueError as e:
            heights.append(0)
            heights_err.append((i,j))
            
    fig, ax= plt.subplots(figsize=(8, 4)) 
    plt.plot(heights)
    ax.text(0.01, 0.95, 'Errors: {}'.format(len(heights_err)), transform=ax.transAxes)
    plt.show()

def worldpx2tilepx(worldpx,left_top_bbx_px):
    """
    世界座標をタイル内座標に変換する
    """
    y1 = worldpx[0] - left_top_bbx_px[0] -1
    x1 = worldpx[1] - left_top_bbx_px[1] -1
    return [y1,x1]

def calc_max_theta(distance,earth_r):
    """
    観測点と対象点の角度（radian）を返す
    """
    return distance/(2 *earth_r)
    
def getHorizonDistance_km(h0_km,earth_r):
    return sqrt(pow(h0_km, 2) + 2 * earth_r * h0_km);

def getTargetHiddenHeight_km(d2_km, earth_r):
    if d2_km  target_tile[index]:
        smaller = target_tile[index]
    elif target_tile[index] > observer_tile[index]:
        smaller = observer_tile[index]
    else:
        smaller = observer_tile[index]
        
    return smaller

def get_origin_tile(observer_tile,target_tile,get_smaller_tile_axis):

    x_smaller = get_smaller_tile_axis(observer_tile,target_tile,"x")
    y_smaller = get_smaller_tile_axis(observer_tile,target_tile,"y")

    return [x_smaller,y_smaller]

def get_bigger_diff(observer_tile,target_tile):
    
    x_diff = abs(observer_tile[0] - target_tile[0])
    y_diff = abs(observer_tile[1] - target_tile[1])
    
    if x_diff > y_diff:
        return x_diff
    elif y_diff > x_diff:
        return y_diff
    else:
        return x_diff


#----------【設定箇所】----------#

#ご自身のAPIキーを設定してください
#参考：https://sorabatake.jp/5048
TOKEN = 'YOUR-API-KEY'

#地球の半径(km)
earth_r = 8490; #理想大気 （実際の半径は6371km）

# 見通しを判定したい任意の地点を緯度経度で指定
#例
# raw1 = [33.471744, 135.860882] #樫野埼灯台 （串本町　潮岬 見通し不可）
raw1 = [33.693889, 135.848611] #色川富士見峠 （那智勝浦町 最遠望）

#富士山
raw2 = [35.360833, 138.727500] #富士山 3776m

z=12 #zoomレベル設定
#--------------------------------#

#緯度と経度に分割
lon1=raw1[1]
lat1=raw1[0]
lon2=raw2[1]
lat2=raw2[0]

#タイル座標取得
observer_tile = get_tile_num(lat1,lon1,z)
target_tile = get_tile_num(lat2,lon2,z)

#始点を取得：観測点と対象点を角とする四角形の左上の座標
origin_tile = get_origin_tile(observer_tile,target_tile,get_smaller_tile_axis)

#上の四角形で長辺のタイル数を取得
diff = get_bigger_diff(observer_tile,target_tile)

##タイルを取得
combined_img = get_combined_image(get_astergdem2_dsm, z, origin_tile[0], origin_tile[1], diff+1)
io.imshow(combined_img)

#地球の曲率を含めた2点間の距離
distance_km = vincenty_inverse(lat1, lon1, lat2, lon2, 1)

##世界ピクセル座標を取得
left_top_bbx = num2deg(origin_tile[0], origin_tile[1], z)
left_top_bbx_px = latlon2tile2(left_top_bbx[0], left_top_bbx[1], z) #始点

px1_wpx = latlon2tile2(lon1, lat1, z) #観測点
px2_wpx = latlon2tile2(lon2, lat2, z) #対象点

##タイル内ピクセル座標を取得
px1_tpx = worldpx2tilepx(px1_wpx,left_top_bbx_px) #観測点
y1 = px1_tpx[0]
x1 = px1_tpx[1]
px2_tpx = worldpx2tilepx(px2_wpx,left_top_bbx_px) #対象点
y2 = px2_tpx[0]
x2 = px2_tpx[1]

##2点間のかたむきを取得
radian = get_radian_btw_p1p2(y1, x1, y2, x2)

##2点間の標高データを取得（単位:m）
actual_heights = get_heights_btw_p1p2(combined_img, y1, x1, y2, x2, radian) 
plot_height(actual_heights) #グラフ描画

#2点のカラーコードを取得
observer_color = combined_img[y1][x1]
target_color = combined_img[y2][x2]

#2点の標高を取得（単位:m）
u=1
observer_height = round(calc_height_chiriin_style(observer_color[0],observer_color[1],observer_color[2],u),2) #観測点
# target_height = round(calc_height_chiriin_style(combined_img[y2][x2] [0],combined_img[y2][x2] [1],combined_img[y2][x2] [2],u),2) # 対象点
# 本来は上のコードで対象点の標高を取得するが、標高タイル（ASTER GDEM 2.0）の解像度が 30m メッシュのため、3776mを取得できず、計測に誤差が出る。
# その為、観測点の標高（富士山）を下のように設定。
target_height = 3776

#沈み込み量を取得（単位:m）
shizumikomi = calculate_shizumikomi(observer_height,distance_km,earth_r)

#対象点（富士山）の見た目の標高を取得（単位:m）
h1_mitame = target_height - shizumikomi

#タイル当たりの辺の長さを取得（km）
tile_km = km_per_tile(distance_km,len(actual_heights))

first_hyoko = round(calc_height_chiriin_style( actual_heights[0][0], actual_heights[0][1], actual_heights[0][2],u),2)

# 障害物の見た目の標高を取得する順番を判定
if observer_height == first_hyoko:
    order = "normal"
else:
    order = "reverse"

#標高で取得したタイル数分ループを回す
for indexNum in range(len(actual_heights)):

    if order == "reverse":
        index = (len(actual_heights) -1) - indexNum
    else:
        index = indexNum
        
    #中間の標高を取得
    hyoko = round(calc_height_chiriin_style( actual_heights[indexNum][0], actual_heights[indexNum][1], actual_heights[indexNum][2],u),2)

    #沈み込み量を取得
    d0 = index*tile_km
    shizumikomi = calculate_shizumikomi(observer_height,d0,earth_r)
    
    #中間の見た目の標高を取得
    h2_mitame = hyoko - shizumikomi
    
    #見た目の高さで比較
    distance_km = round(distance_km,3)
    if h1_mitame < 0:
        result="見通し：不可（地平線）"
        break;
    elif h1_mitame < h2_mitame: 
        
        result='''
    見通し：不可（障害物有り）
    障害物までの距離：{}(km)'''.format(d0)
        break;
    else:
        result="見通し：可"
        
print('観測点の標高：{}(km)' .format(observer_height))
print('対象点（富士山）標高：{}(km)' .format(target_height))
print('2点間の距離：{}(km)' .format(distance_km))
print(result)