宙畑では、衛星観測技術である合成開口レーダ(Synthetic Aperture Radar: 以下SAR)についていくつか解析事例を紹介しています。

その中でも、都市や自然物、湖などの構造物や自然物の推定をパウリ分解(Pauli Decomposition)や三成分散乱分解(Freeman-duran Decomposition)と呼ばれる偏波分解手法を用いて可視化した事例があります。これらの手法を用いることによって、散乱成分を表面散乱(一回反射)、二回反射、体積散乱の成分に分解し、構造物と自然物の選定ができるのです。

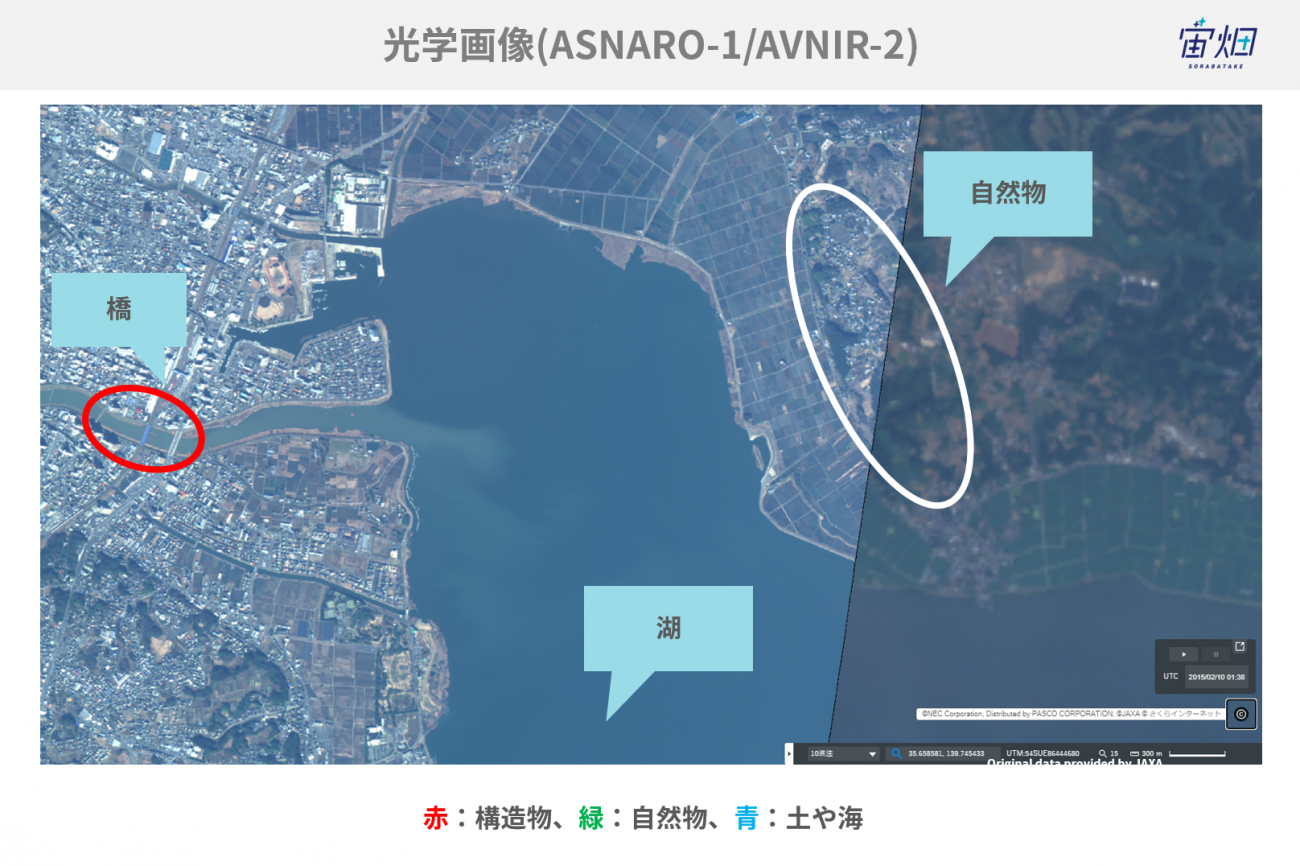
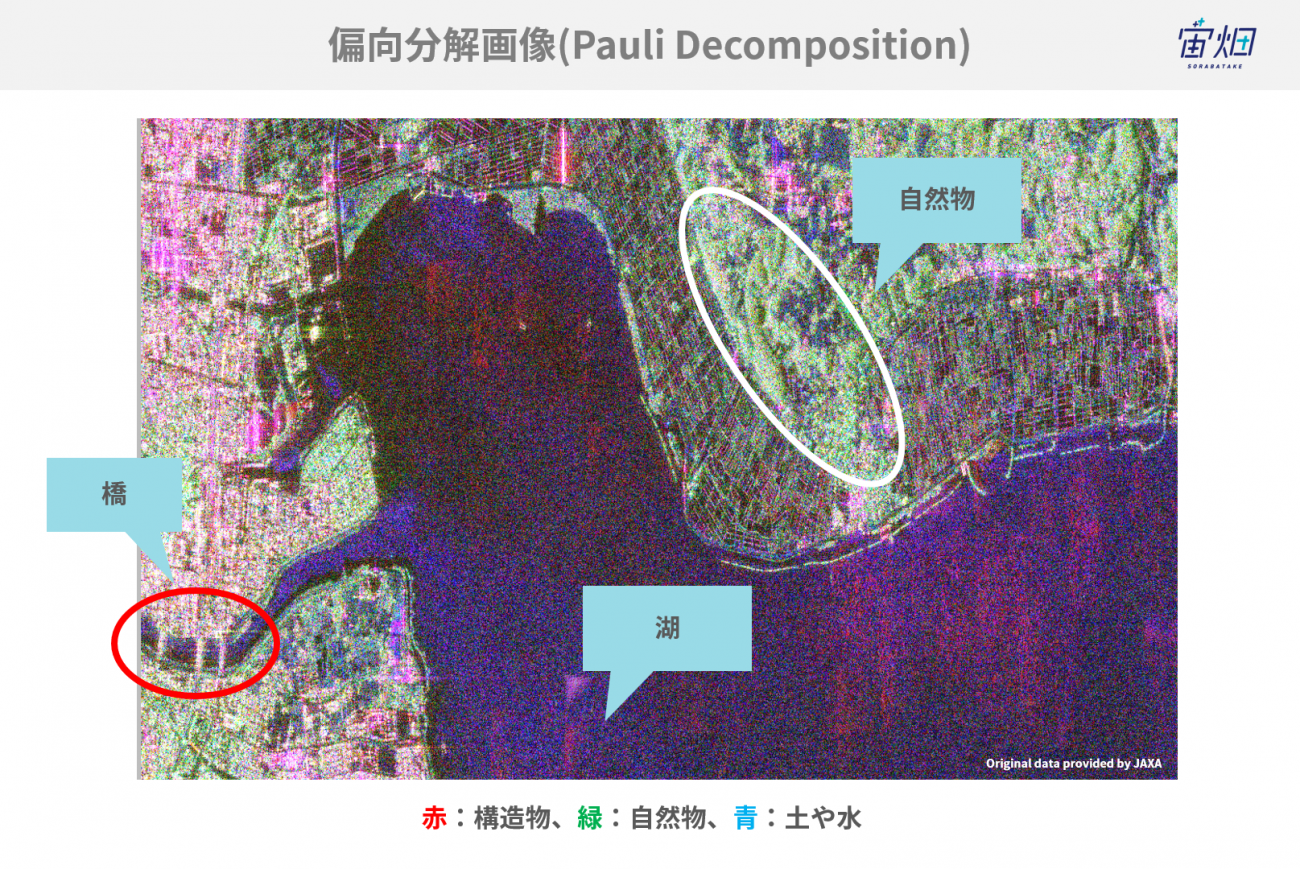
例えば、下記の写真は、霞ヶ浦周辺を解析対象としてパウリ分解や三成分散乱分解を実行した結果です(より詳しく知りたい方は、以下の記事を参考にしてください)。

実行結果に対してパウリ分解や三成分散乱分解を適用することで、自然物や市街地の推定が可能になりました。しかし、様々な形状や材料の建物で構成された都市環境の複雑な散乱特性にあまり対応できてない課題が残っていました。そこで、今回の記事では四成分散乱分解という手法を用いることで、従来の散乱分解手法では検出できなかった「建物に設置されている太陽光パネル」の検出に成功しています。

従来の散乱分解手法の欠点を補う四成分散乱分解を実装する

しかしながら、以前行なってきた散乱分解手法(特に、三成分散乱分解)には主に2つの欠点があります。

・都市域の複雑な散乱特性を考慮していない

以前の記事で取り上げた三成分散乱分解の手法は自然物のような理想的な反射特性を想定しているため、様々な構造物が複雑に入り組んでいる都市域の複雑な散乱特性を表現できていないケースがあります。

具体的には、以前の記事で取り上げた三成分散乱分解の手法は、森林や植生などの散乱要素が一様に分布しているという条件（反射対称性を仮定して）の下でSAR画像を分解しています。

しかしながら、その条件は理想的な場合において成り立つ条件なので、様々な形の建造物が並んでいて複雑な散乱特性を有している都市域においては常に成立するとは限らず、非反射対称性制約が生じてしまいます。

・三成分散乱分解は体積散乱が優位になりやすい

三成分散乱分解における体積散乱の成分がHV偏波のみで算出されている問題があるため、HH偏波やVV偏波の影響が考慮されておらず、体積散乱においてHV偏波が優位になってしまいます。したがって、HH偏波やVV偏波の影響を考慮して体積散乱を調整する必要があります。

これらの問題点を対処するための偏波分解の手法として、四成分散乱分解と呼ばれる手法があります(元論文はこちら：Four-component scattering model for polarimetric SAR image decomposition – IEEE Journals & Magazine)。これによって、より詳細に地域の散乱特性を把握することができ、元々のデータに潜在的に存在する新しい知見を発見しやすくなります。

四成分散乱分解では、その名の通り4つの散乱成分を利用しており、4つ目の散乱成分としてヘリックス散乱と呼ばれるものを導入しています。

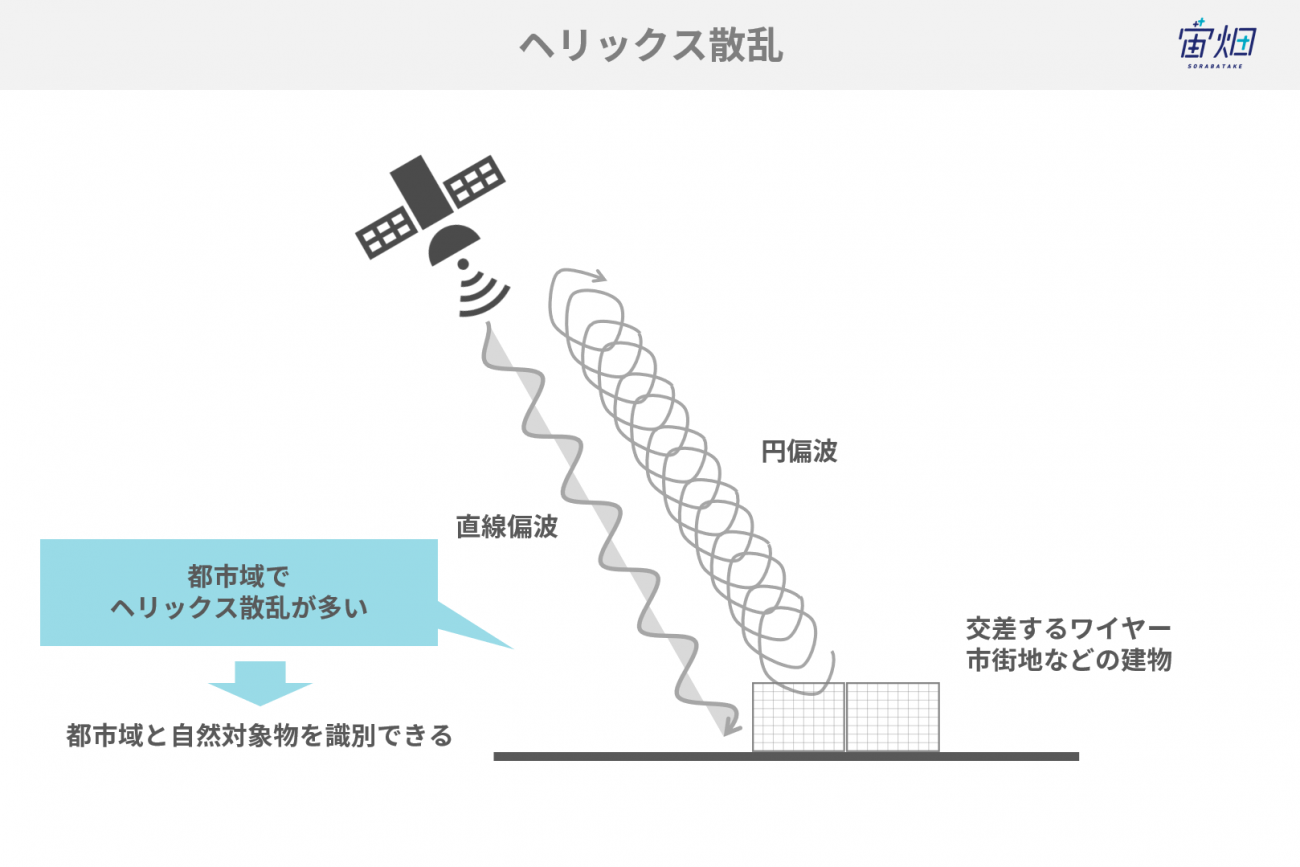
ヘリックス散乱とは直線偏波の入射波を円偏波の反射波に変化させる散乱プロセスです。交差したワイヤや、市街地の建物などから発生します。

ヘリックス散乱を用いて反射対称性が成立する場合とそうでない場合を分離することで、都市域の複雑な散乱と自然な分散散乱を分離することを可能にしています。

また、体積散乱の理論的なモデリングにおいては、植生(雑草など)がランダムな方向を向いていると仮定していますが、森林の木の幹の散乱は垂直に立っていることが多いです。そこで、四成分散乱分解はこれらの条件に対応させるために体積散乱行列を変更させることで修正を行なっています。

四成分散乱分解の実装方法

四成分散乱分解のアルゴリズムの具体的な実装方法についてですが、非常に長い説明となってしまうため、重要な部分だけをかいつまんで説明したいと思います。使用するデータはフルポラリメトリックSARのデータでHH,HV,VV偏波を利用します。TellusのSAR画像を取得する記事は別の記事で紹介しているので、参考にしていただければと思います。

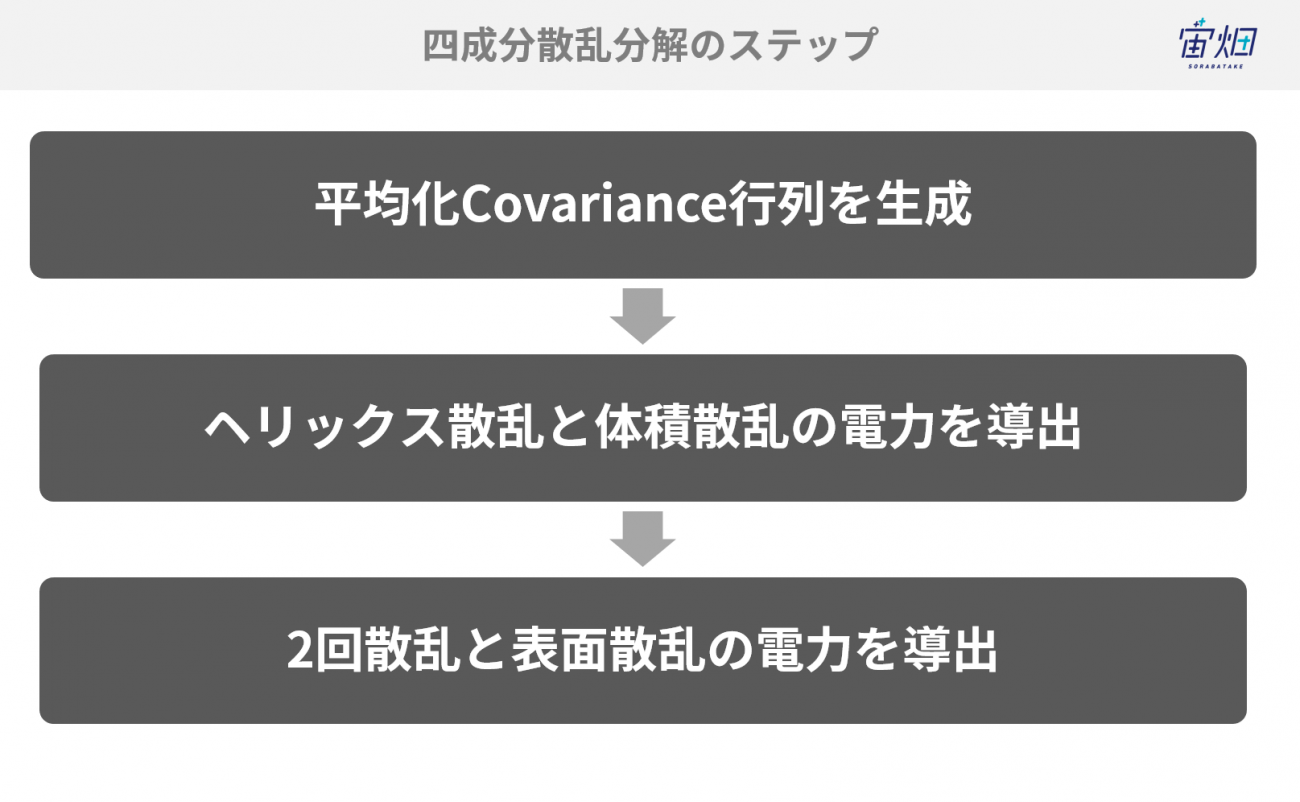
以下に、上記の手順を細かく分けた具体的な導出方法について解説していきます。

①平均化Covariance行列を生成する

まず初めに、HH,HV,VVの偏波成分をそれぞれ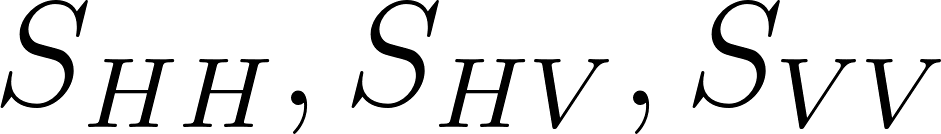とおいて、以下のような行列を生成して、一部の情報を保存します(写真は元論文から抜粋)。＜＞の記号は空間平均を意味していて、今回は3×3の範囲で画像の値を空間平均化処理しています。このような処理を実行することによって、SAR特有のノイズであるスペックルを低減させることができます※もう少し具体的に述べると、二次統計量に変換してから平均化処理をすることによって、大事な情報を失うことなくノイズを減らすことが可能になってます。

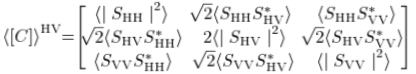
②ヘリックス散乱の電力を導出する

以下の式に従い、ヘリックス散乱を導出していきます。

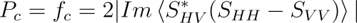
次に、先ほど述べた体積散乱行列の修正を行います。具体的には、以下の図にしたがって、値に応じて体積散乱行列を変更していきます(図は元論文より抜粋)。

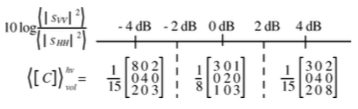
③体積散乱の電力を導出する

以下の式に基づいて、体積散乱の電力を導出します。

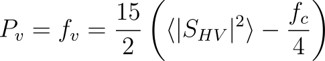
④連立方程式を解く

以下の複数の式で構成された連立方程式を解いて、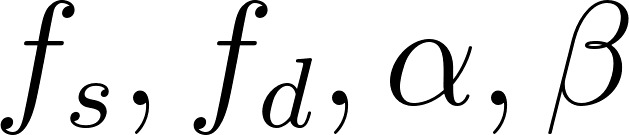を求めます。

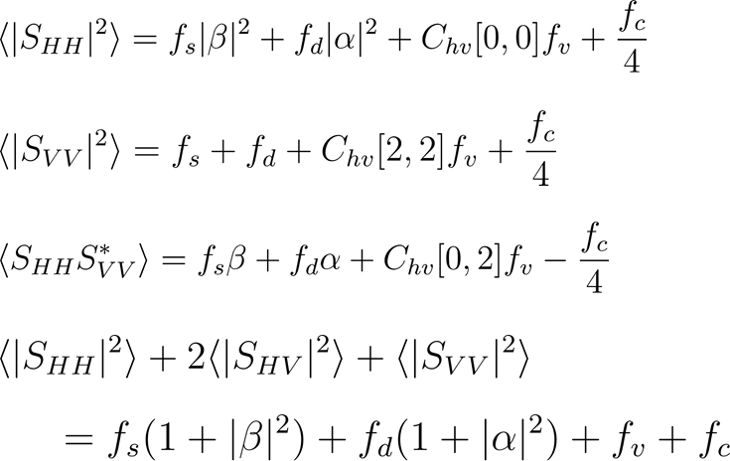
ただし、最後の方程式については、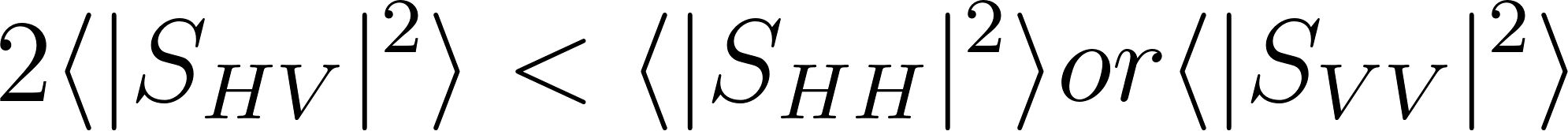が成り立った時のみ使用される形になっており、この条件を満たさない場合は通常の三成分散乱分解のアプローチで問題を解いていきます。

⑤表面散乱と二回散乱の電力を導出する

最後に、上記の連立方程式から得られた解を用いて表面散乱と二回散乱の電力を導出する

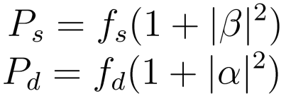
これにより、四つの散乱成分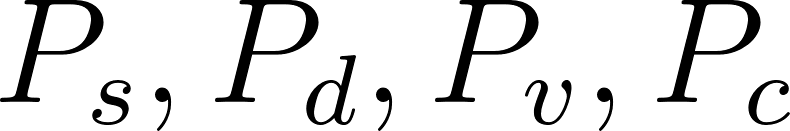を求めることができます。したがって、今までのアルゴリズムをまとめると以下のようにまとめることができます(元論文から抜粋)

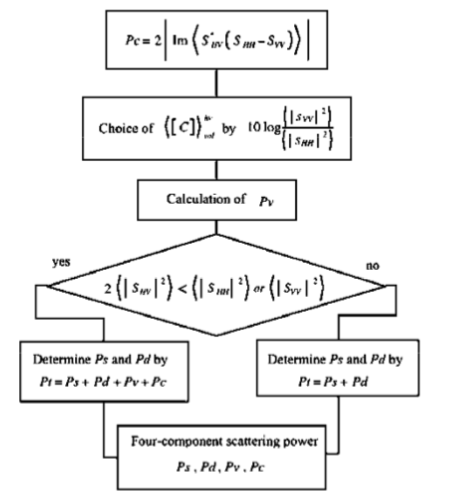
実際に上記の手順を反映したソースコードが下記になります。
まずは、空間平均化処理を施したCovariance行列を生成して、解析に必要な情報を保存していきます。

import numpy as np
def blur(a):
    kernel = np.array([[1.0,1.0,1.0], [1.0,1.0,1.0], [1.0,1.0,1.0]])
    kernel = kernel / np.sum(kernel)
    arraylist = []
    for y in range(3):
        temparray = np.copy(a)
        temparray = np.roll(temparray, y - 1, axis=0)
        for x in range(3):
            temparray_X = np.copy(temparray)
            temparray_X = np.roll(temparray_X, x - 1, axis=1)*kernel[y,x]
            arraylist.append(temparray_X)

    arraylist = np.array(arraylist)
    arraylist_sum = np.sum(arraylist, axis=0)
    return arraylist_sum

def Decomposition(HH,HV,VV,x,y):
    
    SHH = np.zeros((x,y), dtype=np.complex)
    SHV = np.zeros((x,y), dtype=np.complex)
    SVV = np.zeros((x,y), dtype=np.complex)
    SHHSVV = np.zeros((x,y), dtype=np.complex)
    SHHSHV = np.zeros((x,y), dtype=np.complex)
    SHVSVV = np.zeros((x,y), dtype=np.complex)
    
    
    for i in range(x):
        for j in range(y):
            a = HH[i,j]
            c = VV[i,j]
            b = HV[i,j]
            
            SHH[i,j] = (np.absolute(a))**2
            SHV[i,j] = (np.absolute(b))**2
            SVV[i,j] = (np.absolute(c))**2
            SHHSVV[i,j] = (a*c.conjugate())
            SHHSHV[i,j] = (a*b.conjugate())
            SHVSVV[i,j] = (b*c.conjugate())    
            
    SHH = blur(SHH)
    SHV = blur(SHV)
    SVV = blur(SVV)
    np.save('/SHH',SHH)
    np.save('/SHV',SHV)
    np.save('/SVV',SVV)
    np.save('/SHHSVV',SHHSVV)
    np.save('/SHHSHV',SHHSHV)
    np.save('/SHVSVV',SHVSVV)

HH = np.load('/HH.npy')
HV = np.load('/HV.npy')
VV = np.load('/VV.npy')

Decomposition(HH,HV,VV,np.shape(HH)[0],np.shape(HH)[1])

次に、生成した平均化Covariance行列を用いて四成分散乱分解を行います。今回は2000×2000の画像領域を対象にしていますが、実際に行うと2時間近くかかってしまいます。ですので、jupyterでの実行ではなく、例えばdecomp.pyと生成して、

nohup python decomp.py &

とターミナル上でバックグラウンド実行するのをオススメします。
※進捗はターミナルでps uと打てば確認できますし、エラーが起きていればworkディレクトリ上に生成されたnohup.outをcat nohup.outとコマンドを打てば確認できます

import math
import numpy as np
from scipy.optimize import newton_krylov
import scipy.linalg as linalg
from scipy import optimize

SHH = np.load('/SHH.npy')
SHV = np.load('/SHV.npy')
SVV = np.load('/SVV.npy')
SHH_SVV = np.load('/SHHSVV.npy')
SHH_SHV = np.load('/SHHSHV.npy')
SHV_SVV = np.load('/SHVSVV.npy')
rows = np.shape(SHH)[0]
cols = np.shape(SHH)[1]
    
surface = np.zeros(shape=(rows, cols), dtype=np.float64)
double = np.zeros(shape=(rows, cols), dtype=np.float64)
scatter = np.zeros(shape=(rows, cols), dtype=np.float64)
helix = np.zeros(shape=(rows, cols), dtype=np.float64)
    
for x in range(rows):
    for y in range(cols):
        fc = 2 * np.absolute((SHH_SHV[x,y]+SHV_SVV[x,y]).imag)
        if 10*np.log10((np.absolute(SVV[x,y]))/(np.absolute(SHH[x,y])))>2:
            hv = np.array([[3,0,2],
                         [0,4,0],
                         [2,0,8]])
            Chv = (1/15)*hv
        if 10*np.log10((np.absolute(SVV[x,y]))/(np.absolute(SHH[x,y])))<-2:
            hv = np.array([[8,0,2],
                         [0,4,0],
                         [2,0,3]])
            Chv = (1/15)*hv
        else:
            hv = np.array([[3,0,1],
                         [0,2,0],
                         [1,0,3]])
            Chv = (1/8)*hv
        fv = np.absolute((2*SHV[x,y] - fc/2)*(1/Chv[1,1]))
        
        if (2*SHV[x,y] < SHH[x,y]) or (2*SHV[x,y] x[0],fd->x[1],a->x[2],b->x[3]
            def F(x):
                return [
                    x[0]*(1+np.absolute(x[3])**2) + x[1]*(1+np.absolute(x[2])**2),
                    x[0]*(np.absolute(x[3])**2) + x[1]*(np.absolute(x[2])**2),
                    x[0] + x[1],
                    x[0]*x[3] + x[1]*x[2]
                    ]
            guess = [
                2*(np.absolute(SHV[x,y])) + (np.absolute(SHH[x,y])) + (np.absolute(SVV[x,y])) - fv - fc,
                np.absolute(SHH[x,y]) - Chv[0,0]*fv - 0.25*fc,
                np.absolute(SVV[x,y]) - Chv[2,2]*fv - 0.25*fc,
                np.absolute(SHH_SVV[x,y]) - Chv[0,2]*fv + 0.25*fc
            ]   
        elif (2*SHV[x,y] > SHH[x,y]) or (2*SHV[x,y] > SVV[x,y]):
            # fs->x[0],fd->x[1],a->x[2],b->x[3]
            def F(x):
                return [
                x[0]*(1+np.absolute(x[3])**2) + x[1]*(1+np.absolute(x[2])**2),
                x[0]*(np.absolute(x[3])**2) + x[1]*(np.absolute(x[2])**2),
                x[0] + x[1],
                x[0]*x[3] + x[1]*x[2]
                ]
            guess = [
                2*(np.absolute(SHV[x,y])) + (np.absolute(SHH[x,y])) + (np.absolute(SVV[x,y])),
                np.absolute(SHH[x,y]),
                np.absolute(SVV[x,y]),
                np.absolute(SHH_SVV[x,y])
            ]
        result = optimize.root(F, guess, method="lm")
        if SHH_SVV[x,y].real0:
            result.x[2]=-1
        surface[x,y] = int((result.x[0])*(1+np.absolute(result.x[3])**2))
        double[x,y] = int((result.x[1])*(1+np.absolute(result.x[2])**2))
        scatter[x,y] = int(fv)
        helix[x,y] = int(fc)

np.save('/fs',surface)
np.save('/fd',double)
np.save('/fv',scatter)
np.save('/fc',helix)

最後に、以下のコードで可視化を行います。

import cv2
import matplotlib.pyplot as plt
surface = np.load('/fs.npy')
double = np.load('/fd.npy')
scatter = np.load('/fv.npy')
helix = np.load('/fc.npy')

# np.log10の計算をするときにゼロが入るとinfになってしまうため、その対策手段
surface[surface==0]=1
double[double==0]=1

# 表面散乱
sigma = ((10*np.log10(abs(surface))-82-32) + (10*np.log10(abs(helix))-82-32))/2
sigma = np.array(255*(sigma-np.amin(sigma))/(np.amax(sigma)-np.amin(sigma)),dtype="uint8")
fs = cv2.equalizeHist(sigma)

# 二回散乱
sigma = 10*np.log10(abs(double))-82-32
sigma = np.array(255*(sigma-np.amin(sigma))/(np.amax(sigma)-np.amin(sigma)),dtype="uint8")
masks = np.where(sigma > 200, 1, 0)
fd = cv2.equalizeHist(sigma)

# 体積散乱(これだけヒストグラム平坦化の処理を加えない)
sigma = ((10*np.log10(abs(scatter))-82-32) + (10*np.log10(abs(helix))-82-32))/2
sigma = np.array(255*(sigma-np.amin(sigma))/(np.amax(sigma)-np.amin(sigma)),dtype="uint8")
fv = sigma

img=np.zeros((2000, 2000, 3), np.uint8)
img[:,:,0]=fd
img[:,:,1]=fv
img[:,:,2]=fs
img = cv2.GaussianBlur(img,(5,5),0)

# コントラスト強調
min_table = 90
max_table = 255
diff_table = max_table - min_table
look_up_table = np.arange(256, dtype = 'uint8')
for i in range(0, min_table):
    look_up_table[i] = 0
for i in range(min_table, max_table):
    look_up_table[i] = 255 * (i - min_table) / diff_table
for i in range(max_table, 255):
    look_up_table[i] = 255

img = cv2.LUT(img, look_up_table)

plt.figure()
plt.imshow(img)
plt.imsave('sample.png', img)

解析結果

実際に可視化した結果が以下のようになります。解析対象は霞ヶ浦周辺のSAR画像で、前回行なったパウリ分解や三成分散乱分解で使用した地域と同じです。

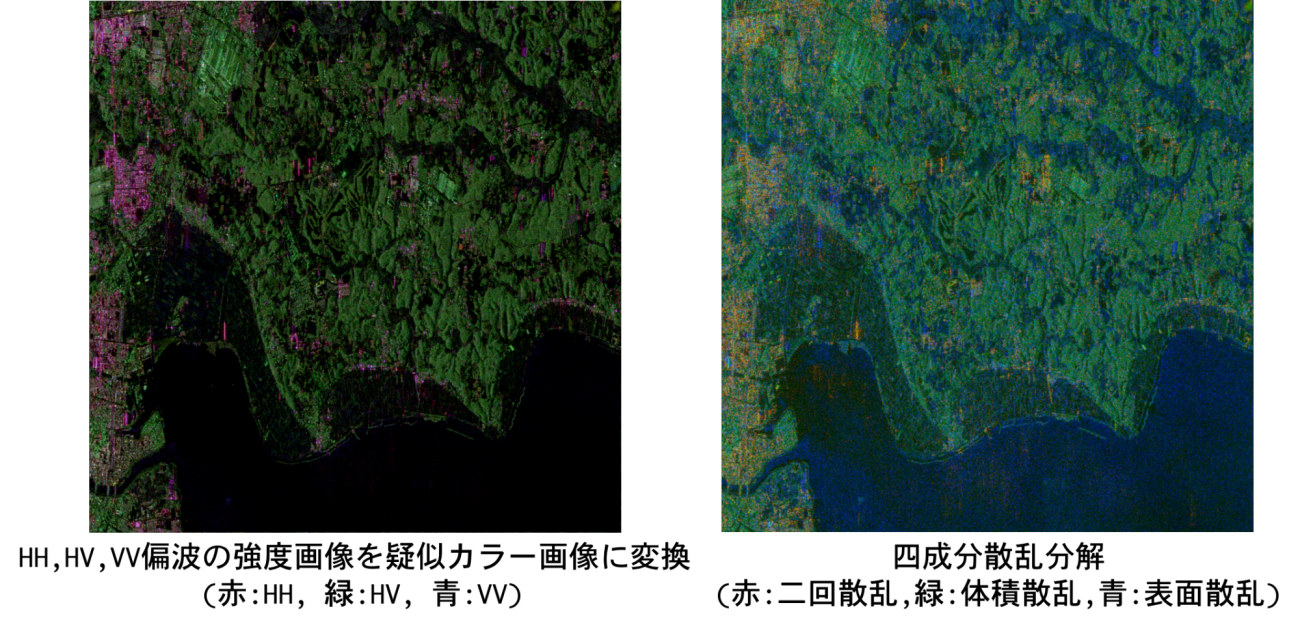
左側が、SARの元々の後方散乱係数を強度画像に変換したもの、右側が四成分散乱分解の結果になります(実際の結果にコントラスト強調やヒストグラム平坦化などを行なって調整してあります。SAR画像のコントラスト強調やヒストグラム平坦化については以下のサイトを参考にしてください→SAR画像の見た目を基本的な画像処理で一瞬に改善する方法)。左側の疑似カラー画像は全ての偏波成分においてコントラスト調整とヒストグラム平坦化を施していますが、右側の四成分散乱分解については、体積散乱のみヒストグラム平坦化を行なっていないので注意してください。また、コントラスト調整は今回はmin_tableの値とmax_tableの値をソースコードの形で固定してますが、本解析の場合はmin_tableを60以上にするとノイズも減っているのが目視で確認しやすいと思います。

ヘリックス散乱については、緑色と青色に均等に割り振っています(本当は赤色と緑色にした方が市街地がより鮮明に見えるのですが、思った以上に霞ヶ浦周辺の湖の二回散乱のノイズが厳しかったので、ヘリックス散乱を緑色と青色に均等に割り振ることで湖のノイズを抑えることに成功しています)。

結果的に、僅かに霞ヶ浦周辺の二回散乱のノイズは残ってしまいましたが、都市域(赤色)や自然物(緑色)、畑や湖(青色)が反映されているので、無事に散乱分解できてることを確認できました。

今回の散乱分解手法によって、市街地に隠れている太陽光パネルを可視化できた！

通常のSAR画像の強度画像と比較して、四成分散乱分解を行なったことによってどんな新しい知見が得られたのか確認していきたいと思います。四成分散乱分解による可視化結果の左下(土浦駅周辺)に注目してみると、下図のように大変興味深い結果が出てきました。

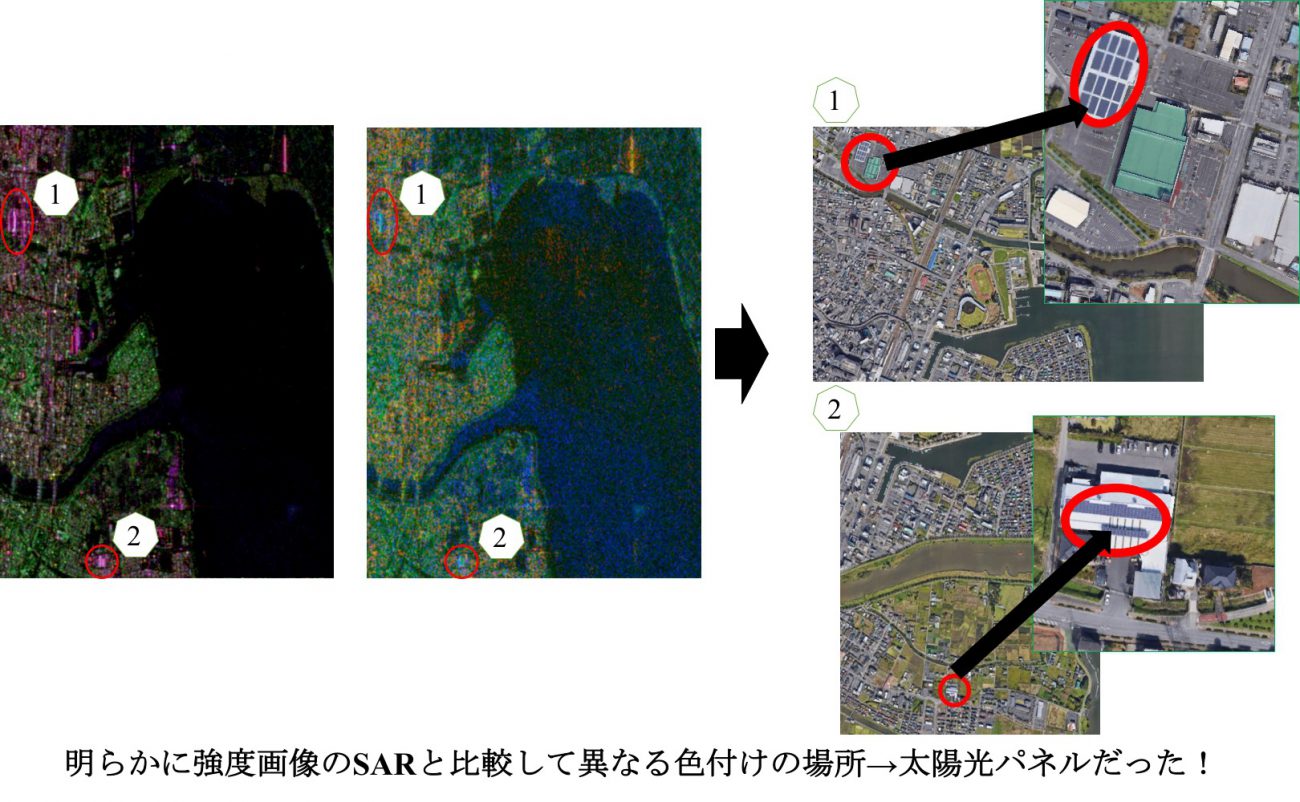
上の図を見ていただけると分かるように、市街地や畑の近くにある建物に設置されている太陽光パネルを検出することができました。

太陽光パネルが検出できた理由についてですが、太陽光パネルにコーディングされている酸化防止膜による表面反射が原因だと思われます。本来は、表面反射のロスを抑えて太陽電池のコストを抑える仕組みが施されているのですが、その影響によるものだと推測できました。

もしこの仮説が正しければ、四成分散乱分解を用いて太陽光パネルの位置を検出し、縦断的に観測することで酸化防止膜の経年劣化のモニタリングができるかもしれません。

このように、純粋にSARの強度画像を疑似カラーにしただけでは発見できないような情報や光学画像では特定に時間を要する対象でも、散乱分解手法を用いて新しい情報を検出できることを実証しました。

まとめ

今回は、四成分散乱分解を用いて通常のSAR画像を強度画像として疑似カラーにした時と比較して、太陽光パネルの検出を可能にすることができました。今後、このようなSAR画像散乱分解によって散乱特性を読み解く技術が進歩することによって、通常だと探すのが困難な都市域の環境情報などを検出することが可能になると思います。

特に、太陽光パネルについては光学画像から探すことは困難だと思いますので、SAR画像の散乱分解手法を通して地域のエコ指標として活躍する可能性もあるかもしれません。今後の課題としては、具体的にこの太陽光パネルがどのような散乱特性を有しているのかをシグネチャ分析などでより詳細にしていくなどの課題が考えられました。

今回の解析手法はGPU環境などが必要なくCPU環境で動作するので、気になる方はぜひTellusに開発環境を申請して解析してみてください！

「Tellus」で衛星データを触ってみよう！

日本発のオープン＆フリーなデータプラットフォーム「Tellus」で、まずは衛星データを見て、触ってみませんか？
★Tellusの利用登録はこちらから