【コード付き】Tellusで干渉SARをやってみた(山編)
地盤沈下などが分かる干渉SARをフルスクラッチで実装します。今回は、山などの起伏のある地形でやってみたいと思います。
記事作成時から、Tellusからデータを検索・取得するAPIが変更になっております。該当箇所のコードについては、以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/access/traveler_api_20220310_
firstpart.html
2022年8月31日以降、Tellus OSでのデータの閲覧方法など使い方が一部変更になっております。新しいTellus OSの基本操作は以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/tellus_os/start_tellus_os.html
Tellusでは、PALSAR-2(JAXAが開発したALOS-2(だいち二号)に搭載されている合成開口レーダ)の標準プロダクトが提供されています。以前こちらで、そのデータを使って「干渉SAR」を実際にやってみるという記事を紹介しました。
【コード付き】地盤の沈降が分かる干渉SAR解析をTellusでやってみた
本記事では、この続編として、山などの起伏のある地形で干渉SARをやってみたいと思います。前回の記事のアルゴリズムでは、軌道縞を手動で除去しているため、起伏のある地形ではキレイに軌道縞を除去することができません。そこで今回は、「軌道縞を軌道情報から推定して除去する」というアルゴリズムを新たに紹介します。
そうすることで、起伏のある地形の干渉画像から、キレイな地形縞を抽出できます。地形縞とは、そのまま地形の高さの測量情報(等高線)になります。つまり、この記事のコードを使えば、誰でも「干渉SARによって標高地図を作る」ことができるようになります!実際の事業や研究向けの実用的なレベルには及びませんが、干渉SARの魅力を肌で感じていただければと思います!
干渉SARとは?
おさらいになりますが、干渉SARとは、一言でいえば、「電波の位相差を測ることで地表面の変化を知る技術」と言えます。衛星が同じ位置から電波を放射したとき、地表面が時期によって変化していれば、それが反射波の位相のずれとして検知されるので、地表面の変化を抽出することができるのです。
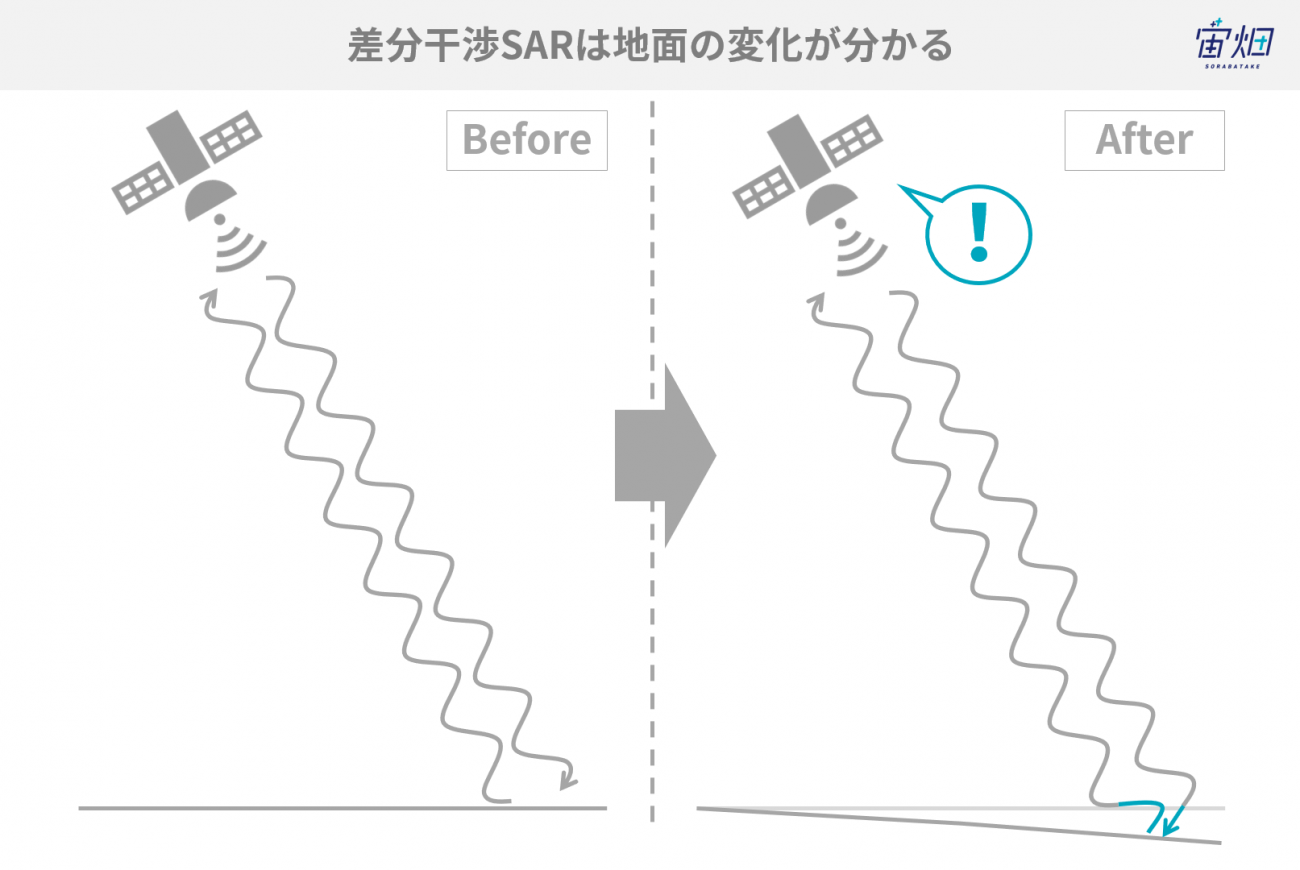
干渉SARの詳しい説明は以前に一般財団法人リモート・センシング技術センター(RESTEC)に解説していただいた記事がありますので、こちらを参照してみてください。
干渉SAR(InSAR)とは-分かること、事例、仕組み、読み解き方-
本記事では、これを実際にTellusの開発環境でプログラミングしていきたいと思います。
干渉ペアをダウンロードする
SAR画像を干渉させるには、いくつか条件があることを前回の記事で説明しました。大事なことは同じ軌道(位置・向き)から観測したものであること、同じ観測モードであること、そして、観測時期が離れすぎていないこと、の3点です。
ALOS-2の場合、ビーム番号、パス番号、フレーム番号、観測モードがすべて一致するプロダクトで干渉可能です。今回は、様々な条件で干渉ペアを探し、干渉結果を確認したうえで良い結果が得られたいくつかの干渉ペアのプロダクトIDを紹介しますので、以下のサンプルコードに従ってダウンロードしてください。
◇ペア1:東京湾埋め立て地周辺
(軌道縞除去アルゴリズムの検証用として、前回の記事で最もキレイに干渉していたペアを使います)
ALOS2237752900-181018
ALOS2260522900-190321
◇ペア2:黒部ダム~立山連峰周辺
ALOS2178980720-170915
ALOS2232800720-180914
◇ペア3:山中湖~富士山周辺
ALOS2176170700-170827
ALOS2229990700-180826
□ダウンロード用サンプルコード
import os, requests
TOKEN = "ご自身のトークンを入力してください"
def publish_palsar2_l11(dataset_id):
url = 'https://file.tellusxdp.com/api/v1/origin/publish/palsar2-l11/{}'.format(dataset_id)
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url, headers=headers)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
return r.json()
def download_file(url, dir, name):
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url, headers=headers, stream=True)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
if os.path.exists(dir) == False:
os.makedirs(dir)
with open(os.path.join(dir,name), "wb") as f:
for chunk in r.iter_content(chunk_size=1024):
f.write(chunk)
def main():
dataset_id == 'プロダクトIDをコピペしてください'
published = publish_palsar2_l11(dataset_id)
for file in published['files']:
file_name = file['file_name']
file_url = file['url']
#サムネイル画像、HH偏波の画像、サマリテキストファイル、リーダファイルのみをダウンロードします
if "jpg" in file_name or "IMG-HH" in file_name or "summary" in file_name or "LED" in file_name:
print(file_name)
file = download_file(file_url, dataset_id, file_name)
if __name__=="__main__":
main()
ダウンロードができたら、サムネイル画像が以下のものになっているかを確認して次に進んでください。
強度画像と位相画像を出力
それぞれのプロダクトから、強度画像と位相画像を出力します。
ここは前回の記事のコードとほぼ同じです。画像全体では、サイズが大きすぎてメモリエラーとなるため、範囲を指定して出力します。範囲はペアごとに異なります。
また、干渉解析のステップごとに、Numpy配列を出力・保存して、次のステップで読み込んで利用することで、ステップごとにコードを改良しやすいように工夫しています。また、記事中に一度記載したインポートモジュール、関数は、2度目以降は省略していきます。
□サンプルコード
import os
import numpy as np
import struct
import math
from io import BytesIO
import cv2
def get_slc(fp,pl):
fp.seek(236)
nline = int(fp.read(8))
fp.seek(248)
ncell = int(fp.read(8))
nrec = 544 + ncell*8
nline = pl[3]-pl[2]
fp.seek(720)
fp.seek(int((nrec/4)*(pl[2])*4))
data = struct.unpack(">%s"%(int((nrec*nline)/4))+"f",fp.read(int(nrec*nline)))
data = np.array(data).reshape(-1,int(nrec/4))
data = data[:,int(544/4):]
data = data[:,::2] + 1j*data[:,1::2]
data = data[:,pl[0]:pl[1]]
sigma = 20*np.log10(abs(data)) - 83.0 - 32.0
phase = np.angle(data)
sigma = np.array(255*(sigma - np.amin(sigma))/(np.amax(sigma) - np.amin(sigma)),dtype="uint8")
sigma = cv2.equalizeHist(sigma)
return sigma, phase
def main():
#例としてペア1を実施します。
#二つの画像に対してコメントアウトを入れ替えて2度実行してください。
dataset_id = 'ALOS2237752900-181018'
#dataset_id = 'ALOS2260522900-190321'
img = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-UBSR1.1__D'),mode='rb')
#範囲を指定する配列(実施するペアによって、コメントアウトを入れ替えてください)
pl = [2500, 4500, 12000, 14000] #ペア1用
#pl = [5000, 7500, 13000, 15500] #ペア2用
#pl = [3750, 7450, 8500, 10500] #ペア3用
#複素画像の取得
sigma, phase = get_slc(img,pl)
#強度、位相画像の出力(2つの画像に対してコメントアウトを入れ替えて二度実行)
np.save('sigma01.npy',sigma) #numpy配列として出力
np.save('phase01.npy',phase) #numpy配列として出力
#np.save('sigma02.npy',sigma) #numpy配列として出力
#np.save('phase02.npy',phase) #numpy配列として出力
#強度画像の出力・保存
plt.figure()
plt.imsave('sigma.png', sigma,cmap='gray', vmin = 0, vmax = 255)
plt.imsave('phase.png', phase,cmap='jet', vmin = 0, vmax = 255)
if __name__=="__main__":
main()
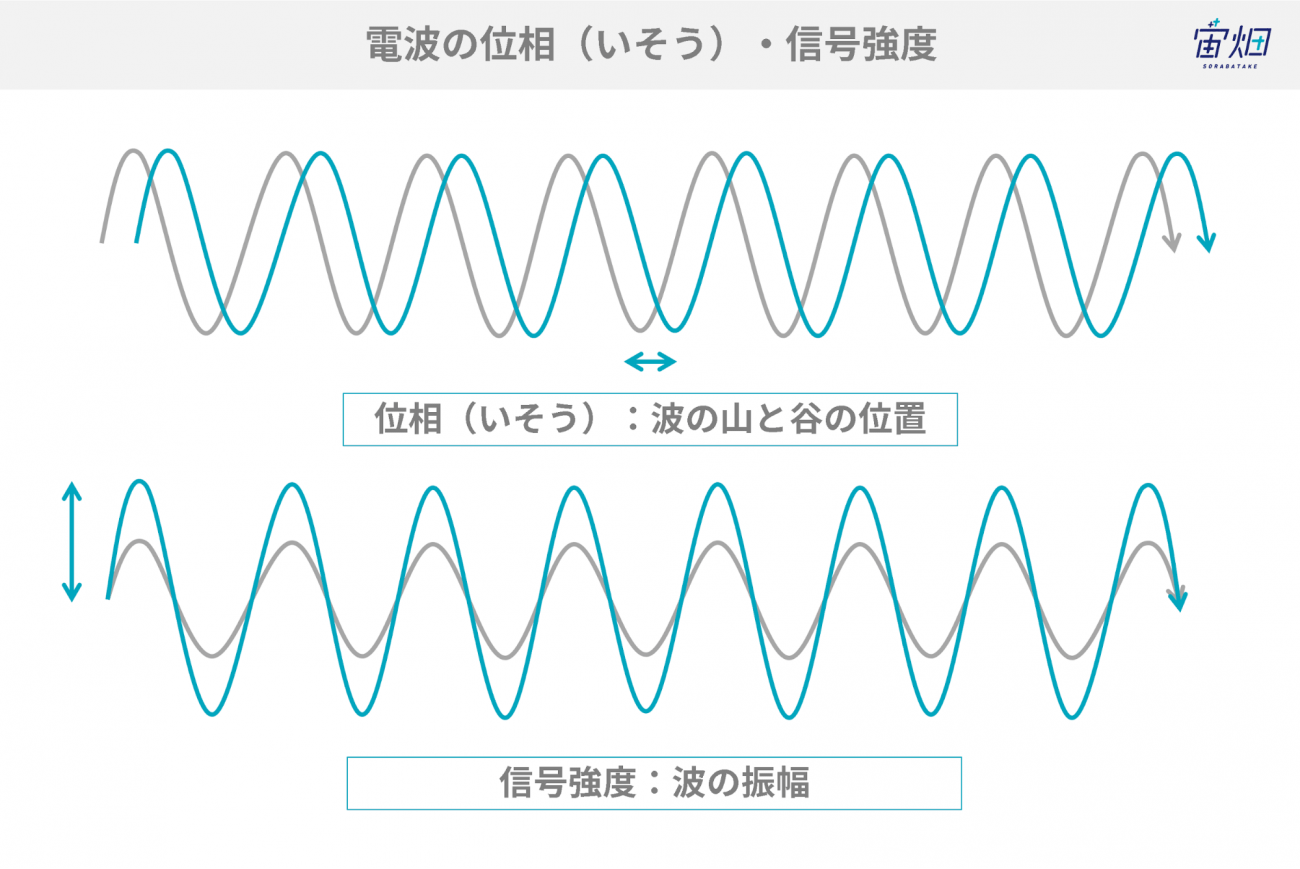
これによって得られた画像は以下の通りです。各ペアの1枚目と2枚目はほぼ同じ画像なので、1枚目のみ表示します。強度画像は、反射係数を校正して対数化し、さらにOpenCVの機能を使ってヒストグラムを平坦化しています。また、位相画像は、-180度~+180度(-π~+π)にラップされています。


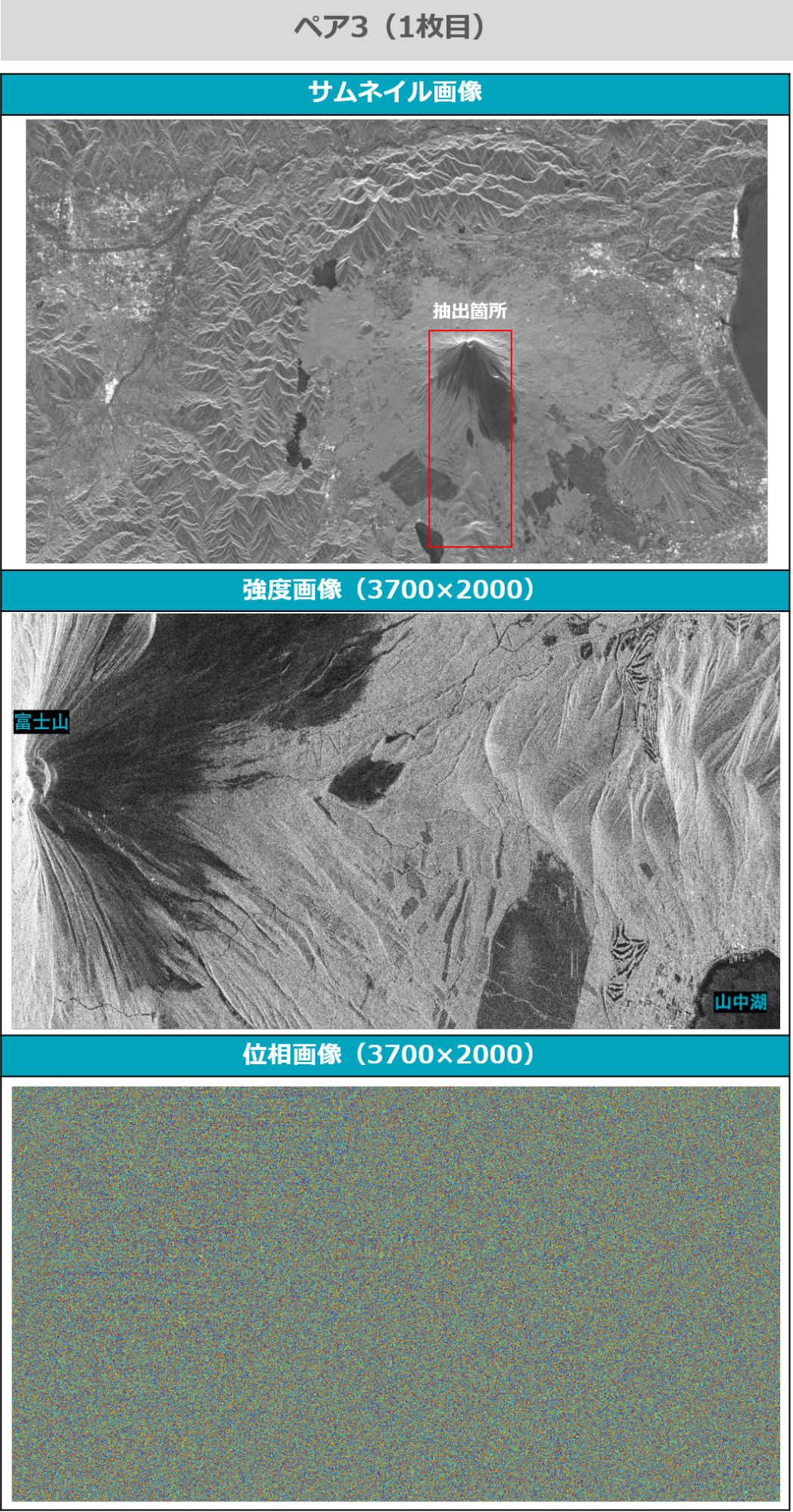
強度画像は6m解像度ですが、地形を認識するためには十分な解像度です。各画像は200~3700ピクセルありますので、実際にダウンロードしてみていただくことをお勧めします。
また、位相画像にまったく視認性がないことは、前回の記事でも触れたとおりです。位相情報が意味を持つのは、干渉解析など、他の画像との差分を抽出した時になります。しかし、正確に干渉させるためには、二つの画像の位置をピッタリ合わせる必要があるので、その位置合わせを行うために強度画像が必要、ということでしたね。
では、上記のプログラムを用いて、それぞれのペアの、位置合わせをするために用いる2枚の強度画像と、干渉させる2枚の位相画像を出力できたら、次のステップへ進んでください。
干渉処理
SAR画像を干渉させるとはどういうことかについては、前回の記事で詳細に触れました。一言でいえば、「強度画像で位置を合わせて、位相画像の差分を取ること」です。この処理も、基本的に前回のコードとほぼ同じです。以下のコードをコピペして実行してください。
□サンプルコード
#画像の位置合わせを行う関数
def coregistration(A,B,C,D):
py = len(A)
px = len(A[0])
A = np.float64(A)
B = np.float64(B)
d, etc = cv2.phaseCorrelate(B,A)
dx, dy = d
if dx >= 0 and dy >= 0:
dx = int(np.round(dx))
dy = int(np.round(dy))
rD = D[0:py-dy,0:px-dx]
rC = C[dy:py,dx:px]
elif dx = 0:
dx = int(np.round(dx))
dy = int(np.round(dy))
rD = D[0:py-dy,abs(dx):px]
rC = C[dy:py,0:px-abs(dx)]
return rC, rD
def wraptopi(x):
x = x - np.floor(x/(2*np.pi))*2*np.pi - np.pi
return x
def main():
#強度画像と位相画像の読み込み。
phase01 = np.load('phase01.npy')
sigma01 = np.load('sigma01.npy')
phase02 = np.load('phase02.npy')
sigma02 = np.load('sigma02.npy')
coreg_phase01, coreg_phase02 = coregistration(sigma01,sigma02,phase01,phase02)
ifgm = wraptopi(coreg_phase01 - coreg_phase03)
np.save('ifgm.npy',ifgm01)
plt.imsave('ifgm.jpg', ifgm, cmap = "jet")
if __name__=="__main__":
main()
これによって出力された干渉画像(インターフェログラム)は以下の通りです。



ここでわかるのは、ペア1のような、港湾の埋め立て地では、ほとんど地形の起伏がないため、一様な縞模様だけが残っています。これを軌道縞と呼びますが、このように一様な軌道縞なら、前回の記事で紹介したように、画像を目で見て軌道縞を作成して除去することが可能です。しかし、ペア2、ペア3のように、山があって地形が凸凹しているようなところでは、地形縞と軌道縞が混ざってしまい、それらを目視で区別することができません。
そこで本記事では、この軌道縞を、SARの標準プロダクトに格納されている軌道情報から推定するアルゴリズムを紹介します。これによって、軌道縞がキレイに取り除くことで、地形の形に添った地形縞を取得するのが今回のゴールです。
本記事のメインテーマ:軌道情報を使って軌道縞を除去しよう!
軌道縞について、前回の記事よりも詳細に説明をしておきます。
軌道縞とは、2回の観測時の衛星の位置が微妙に違うことによって生じる縞模様です。より正確には、地面と衛星の距離の差分を、レーダの波長で割った余りが、軌道縞の位相成分にあたります。言葉だけでは少し難しいと思いますので、図で解説します。
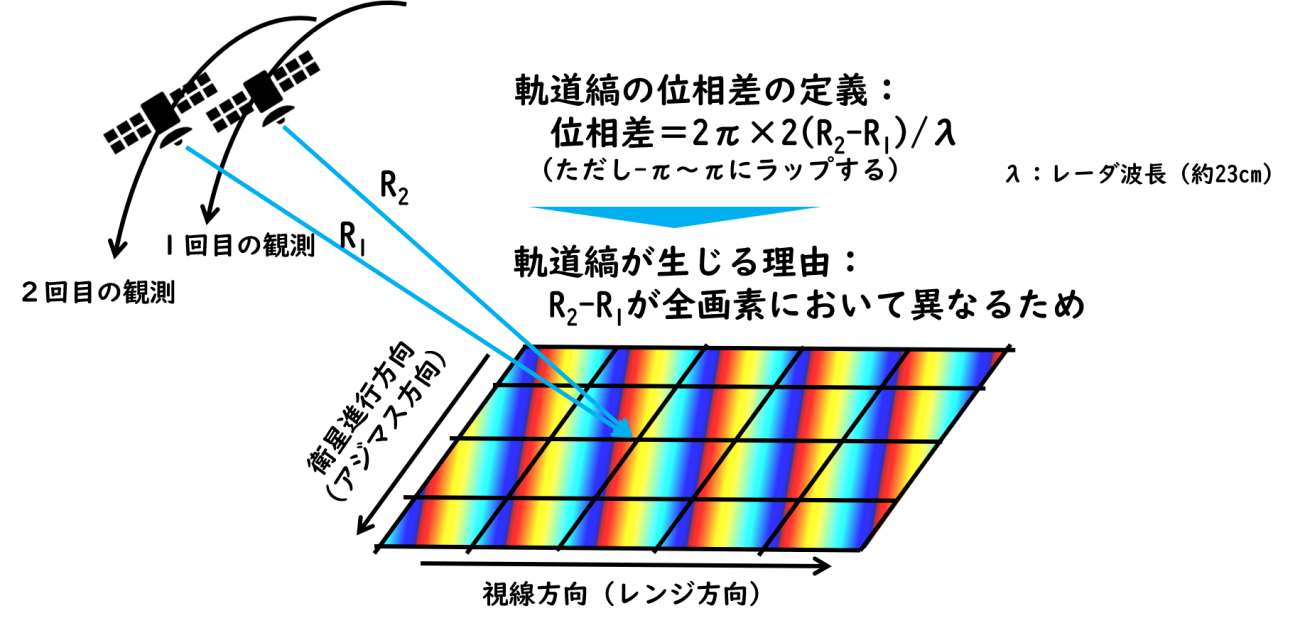
また、実際にはSAR画像は10秒くらいの時間をかけて画像1枚分のエリアを観測しています。その10秒間で衛星は100km程度移動していますので、その移動分を無視することはできません。そこで、画像の各画素が取得された時の衛星の位置を特定するため、観測中の衛星の位置と時刻を記録したデータを用いて、適切に補間していきます。データはCEOSと呼ばれるフォーマットに格納しています(CEOSフォーマットについて、詳しくはこちらの記事をご覧ください。)。こちらも図で内容を理解していただければと思います。
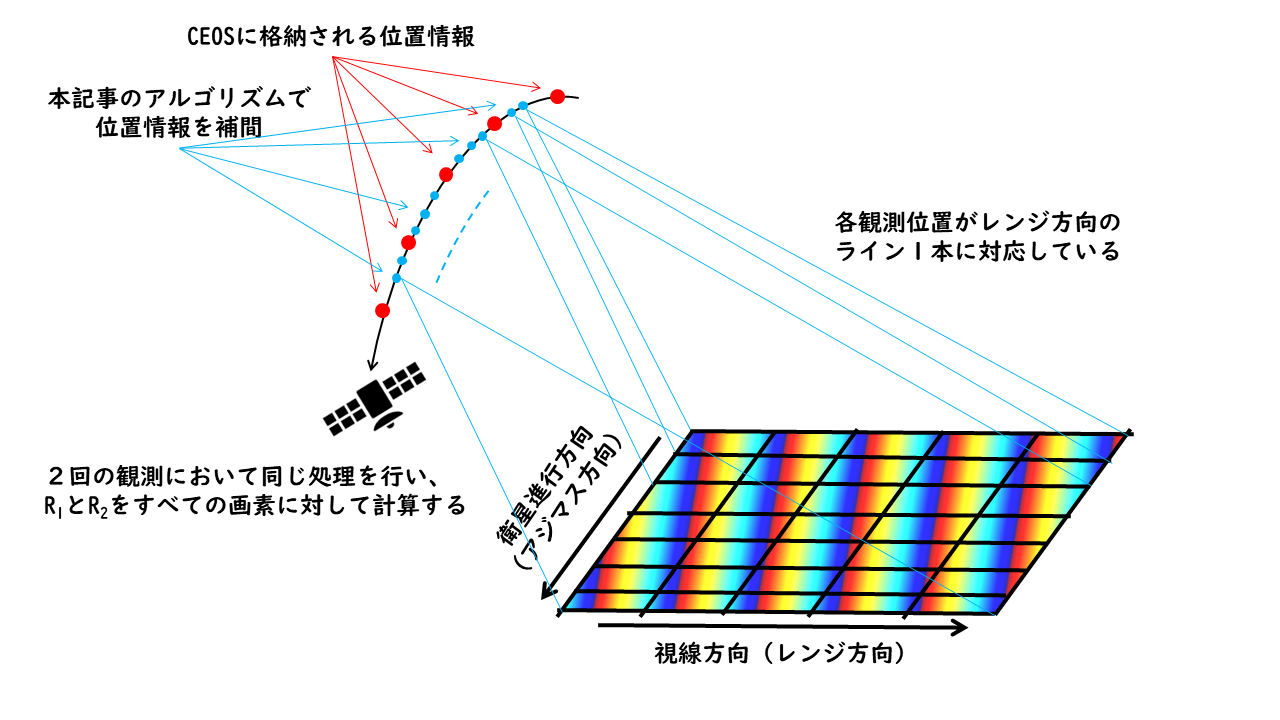
実際のアルゴリズムは、CEOSフォーマットを読み込む非常に難解(煩雑)なものなので、コードをすべて理解する必要はありません。大事なことは、図で説明したような軌道縞を正確に取得するための方法を理解することだと思いますので、ここまでの説明が理解できたら、以下のコードをひとまずコピペして実行してみてください。
□サンプルコード
import scipy
from scipy.interpolate import interp1d
#観測中の衛星位置を出力する関数
def get_sat_pos(led,img):
img.seek(720+44)
time_start = struct.unpack(">i",img.read(4))[0]/1000
led.seek(720+500)
lam = float(led.read(16)) #m
led.seek(720+4096+140)
position_num = int(led.read(4))
led.seek(720+4096+182)
time_interval = int(float(led.read(22)))
led.seek(720+4096+160)
start_time = float(led.read(22))
led.seek(720+68)
center_time = led.read(32)
Hr = float(center_time[8:10])*3600
Min = float(center_time[10:12])*60
Sec = float(center_time[12:14])
msec = float(center_time[14:17])*1e-3
center_time = Hr+Min+Sec+msec;
time_end = time_start + (center_time - time_start)*2;
img.seek(236)
nline = int(img.read(8))
time_obs = np.arange(time_start, time_end, (time_end - time_start)/nline)
time_pos = np.arange(start_time, start_time+time_interval*position_num,time_interval)
pos_ary = [];
led.seek(720+4096+386)
for i in range(position_num):
for j in range(3):
pos = float(led.read(22))
pos_ary.append(pos)
led.read(66)
pos_ary = np.array(pos_ary).reshape(-1,3)
fx = scipy.interpolate.interp1d(time_pos,pos_ary[:,0],kind="cubic")
fy = scipy.interpolate.interp1d(time_pos,pos_ary[:,1],kind="cubic")
fz = scipy.interpolate.interp1d(time_pos,pos_ary[:,2],kind="cubic")
X = fx(time_obs)
Y = fy(time_obs)
Z = fz(time_obs)
XYZ = np.zeros(nline*3).reshape(-1,3)
XYZ[:,0] = X
XYZ[:,1] = Y
XYZ[:,2] = Z
return XYZ
#軌道縞を生成する関数
def get_orbit_stripe(pos1,pos2,pl,led):
led.seek(720+500)
lam = float(led.read(16)) # [m]
a = []
b = []
c = []
led.seek(720+4096+1620+4680+16384+9860+325000+511000+3072+728000+1024)
for i in range(25):
a.append(float(led.read(20)))
for i in range(25):
b.append(float(led.read(20)))
for i in range(2):
c.append(float(led.read(20)))
npix = pl[1]-pl[0]
nline = pl[3]-pl[2]
orb = np.zeros((nline,npix))
for i in range(npix):
if i % 100 == 0:
print(i)
for j in range(nline):
px = i+pl[0]-c[0]
ln = j+pl[2]-c[1]
ilat = (a[0]*ln**4 + a[1]*ln**3 + a[2]*ln**2 + a[3]*ln + a[4])*px**4 + (a[5]*ln**4 + a[6]*ln**3 + a[7]*ln**2 + a[8]*ln + a[9])*px**3 + (a[10]*ln**4 + a[11]*ln**3 + a[12]*ln**2 + a[13]*ln + a[14])*px**2 + (a[15]*ln**4 + a[16]*ln**3 + a[17]*ln**2 + a[18]*ln + a[19])*px + a[20]*ln**4 + a[21]*ln**3 + a[22]*ln**2 + a[23]*ln + a[24]
ilon = (b[0]*ln**4 + b[1]*ln**3 + b[2]*ln**2 + b[3]*ln + b[4])*px**4 + (b[5]*ln**4 + b[6]*ln**3 + b[7]*ln**2 + b[8]*ln + b[9])*px**3 + (b[10]*ln**4 + b[11]*ln**3 + b[12]*ln**2 + b[13]*ln + b[14])*px**2 + (b[15]*ln**4 + b[16]*ln**3 + b[17]*ln**2 + b[18]*ln + b[19])*px + b[20]*ln**4 + b[21]*ln**3 + b[22]*ln**2 + b[23]*ln + b[24]
ixyz = lla2ecef(ilat*np.pi/180.0,ilon*np.pi/180.0,0)
r1 = np.linalg.norm(pos1[j+pl[2],:] - ixyz);
r2 = np.linalg.norm(pos2[j+pl[2],:] - ixyz);
orb[j,i] = wraptopi(2*np.pi/lam*2*(r2-r1));
return orb
#緯度経度高度から地球のECEF座標系のXYZを出力する関数
def lla2ecef(lat,lon,alt):
a = 6378137.0
f = 1 / 298.257223563
e2 = 1 - (1 - f) * (1 - f)
v = a / math.sqrt(1 - e2 * math.sin(lat) * math.sin(lat))
x = (v + alt) * math.cos(lat) * math.cos(lon)
y = (v + alt) * math.cos(lat) * math.sin(lon)
z = (v * (1 - e2) + alt) * math.sin(lat)
return np.array([x,y,z])
def main():
dataset_id = 'ALOS2237752900-181018' #ペア1の1枚目
fpimg = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-UBSR1.1__D'),mode='rb')
fpled = open(os.path.join(dataset_id,'LED-'+dataset_id+'-UBSR1.1__D'),mode='rb')
pos1 = get_sat_pos(fpled,fpimg)
dataset_id = 'ALOS2260522900-190321' #ペア1の2枚目
fpimg = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-UBSR1.1__D'),mode='rb')
fpled = open(os.path.join(dataset_id,'LED-'+dataset_id+'-UBSR1.1__D'),mode='rb')
pos2 = get_sat_pos(fpled,fpimg)
pl = [2500, 4500, 12000, 14000] #ペア1用
#pl = [5000, 7500, 13000, 15500] #ペア2用
#pl = [3750, 7450, 8500, 10500] #ペア3用
orbit_stripe = get_orbit_stripe(pos1,pos2,pl,fpled)
np.save('orbit_stripe.npy',orbit_stripe)
plt.figure()
plt.imsave('orbit_stripe.jpg', orbit_stripe, cmap = "jet")
if __name__=="__main__":
main()
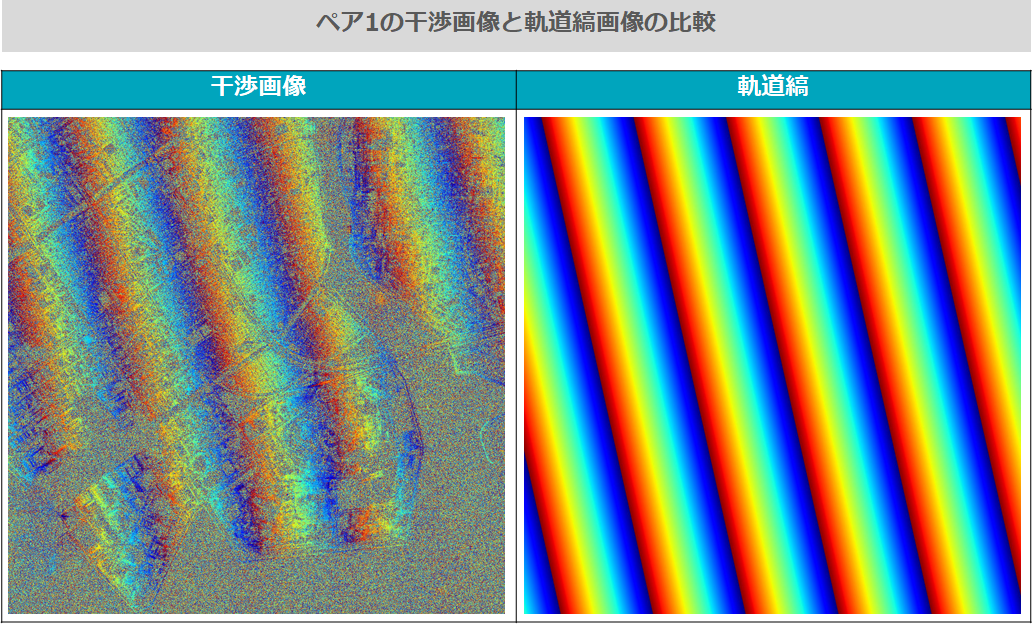
このプログラムによって生成されたペア1の軌道縞画像を以下に示します。ペア1では、地形が平坦なため、干渉縞とほぼ同じ形になっていることがわかります。これで、キレイに軌道縞を除去する準備はできたと言えるでしょう。
軌道縞を除去してみよう
それでは最後に、軌道縞を除去して、キレイな地形縞になるかどうか、確認したいと思います。サンプルコードは簡単で、用意したインターフェログラムと軌道縞を、引き算して[-π~π]へラップするだけです。
def main():
ifgm = np.load('ifgm.npy')
orbit_stripe = np.load('orbit_stripe.npy')
#軌道縞の画像サイズをインターフェログラムのサイズと合わせます
orbit_stripe = orbit_stripe[0:ifgm.shape[0],0:ifgm.shape[1]]
ifgm_sub_orb = wraptopi(ifgm - orbit_stripe) #軌道縞除去の処理
plt.figure()
plt.imsave('ifgm_sub_orb.jpg', ifgm_sub_orb, cmap = "jet")
if __name__=="__main__":
main()
まず、検証用に用意した平坦なペア1の画像でみてみましょう。
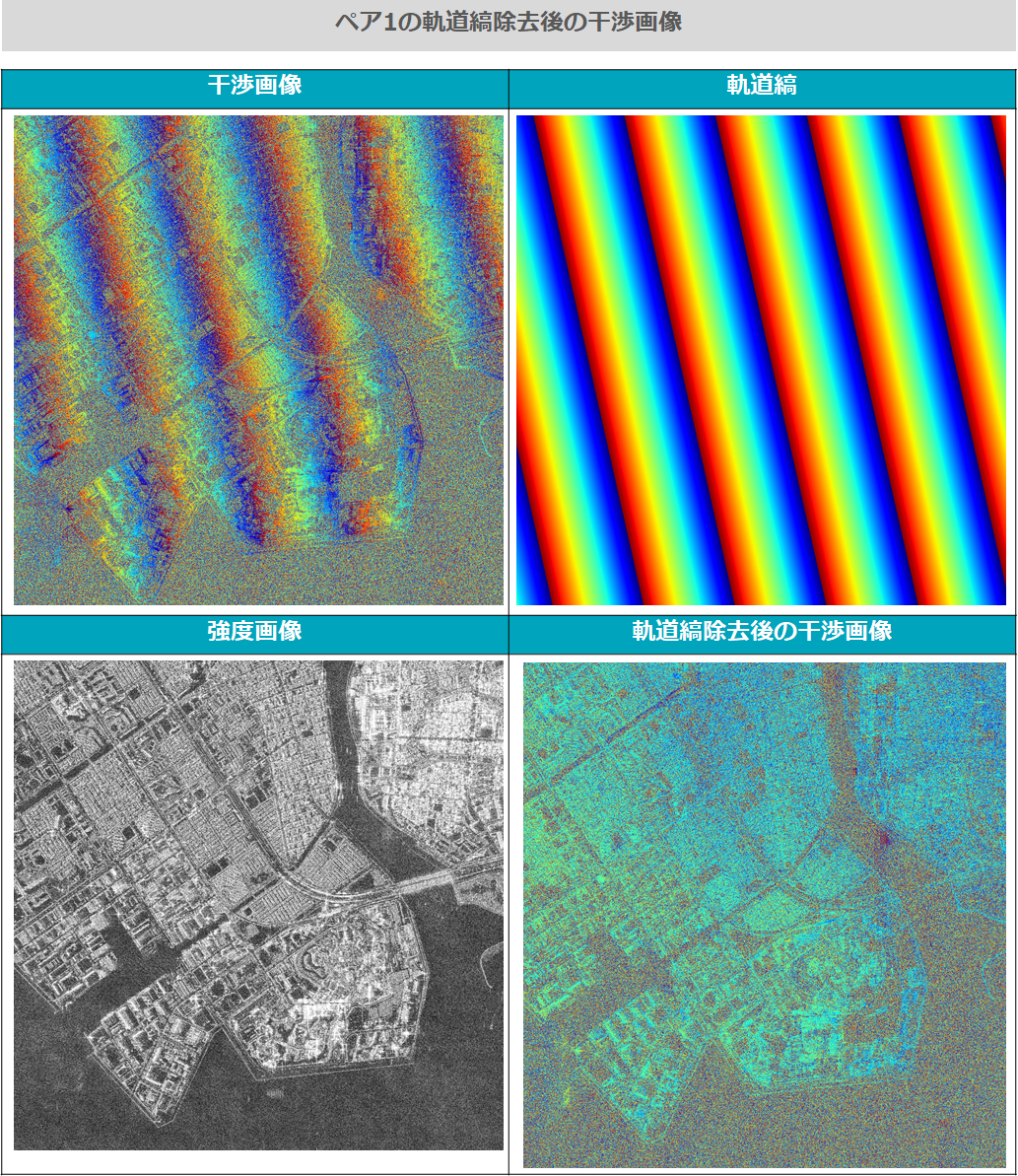
かなりキレイに軌道縞が取り除けていることがわかります。また、前回の記事の実行結果とほぼ同じ結果が得られているので、それなりに精度が出ていると言えそうです。
ではここからが本題で、山などの起伏がある地形での処理結果を示します。なお、出力画像は自然な地形に見えるよう適宜左右・上下反転させています。


軌道縞除去後のインターフェログラムの見方
処理を終えたところで、軌道縞除去後のインターフェログラムから何がわかるか考えてみたいと思います。まず、軌道縞を除去した後のインターフェログラムには、「地形縞」が現れていると考えてください。地形縞とは、一言で言い換えれば等高線のことです。これを利用すれば、SARによって標高測量ができるということになります。
実際にやってみましょう。教科書によると、地形縞の1周期を標高に換算する式は以下のようにあらわすことができます。記号の意味は図の通りです。
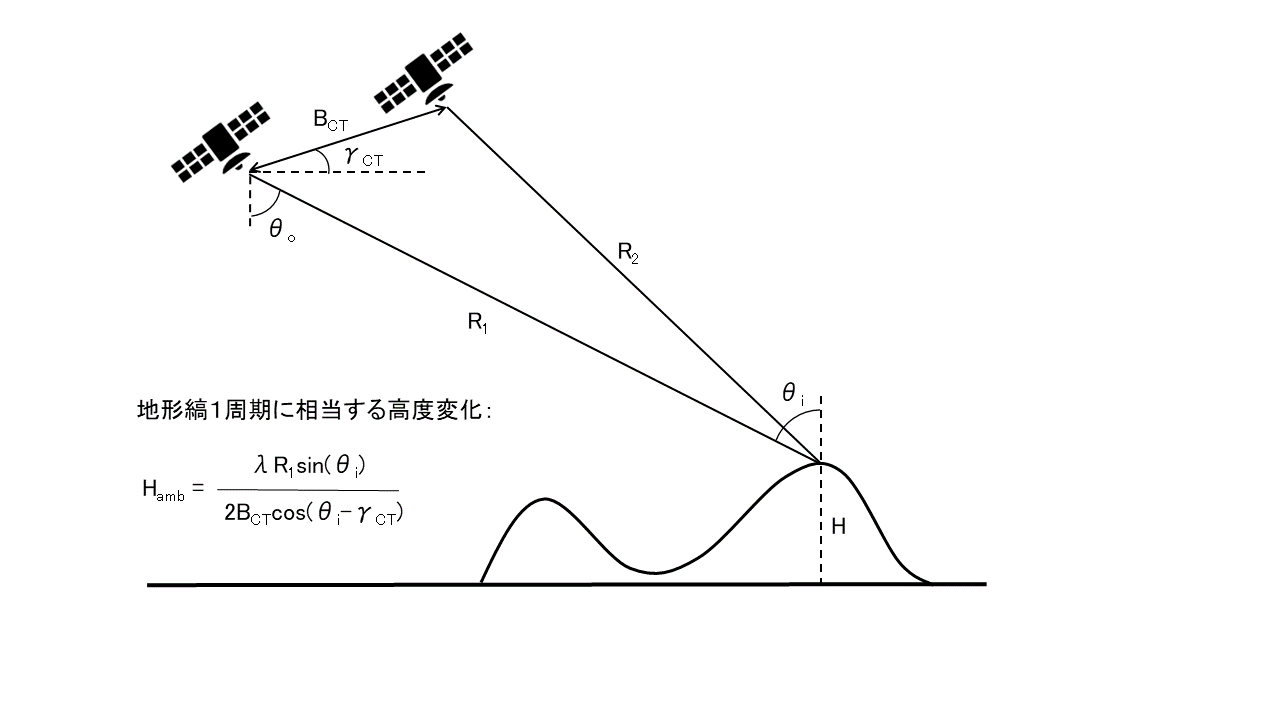
(リモートセンシングのための合成開口レーダの基礎[第2版]大内和夫著, 東京電機大学出版局, p.230, 231を参考に作成)
本来であれば、R1やθiは、画像内の画素すべてにおいて値が異なるので、画像全体にわたって計算していく必要があるのですが、今回は画像の中心付近で代表値を見積もって、計算してみました。

なんと、ざっくりした計算でしたが、標高がピタリと一致しました!ただし、この干渉画像では、全体が1周期の中に納まっていて、波数のカウント(N=0.8の部分)があまり正確ではありません。そこで、ペア3の富士山でも全く同じ計算方法で計算してみました。

計算の結果、富士山の標高は3941mでした。先ほどよりは誤差がありますが、それでも誤差は5%以下ですので、精度はそれなりと言えそうです。そしてこの計算を画像内のすべての画素に対して行えば、画像全体の標高が5%以内の範囲で測量できるということになります。
個人的には、映画「劔岳~点の記~」がとても好きなのですが、命がけで測量していたあの時代を思うと、宇宙からこんなに簡単に測量ができてしまうってすごいな、と改めて思いました。しかも、「点」ではなく「面」で測量できるのが、やはり宇宙から観測する利点であることがよくわかりますね。

まとめ
前回の記事でご紹介した、干渉SARの処理フローを再掲しておきます。今回紹介したアルゴリズムは、フロー中の5項の軌道縞除去を、軌道情報を用いて処理する、ということでした。これで地形が複雑な場所でも、干渉解析が可能になりました。
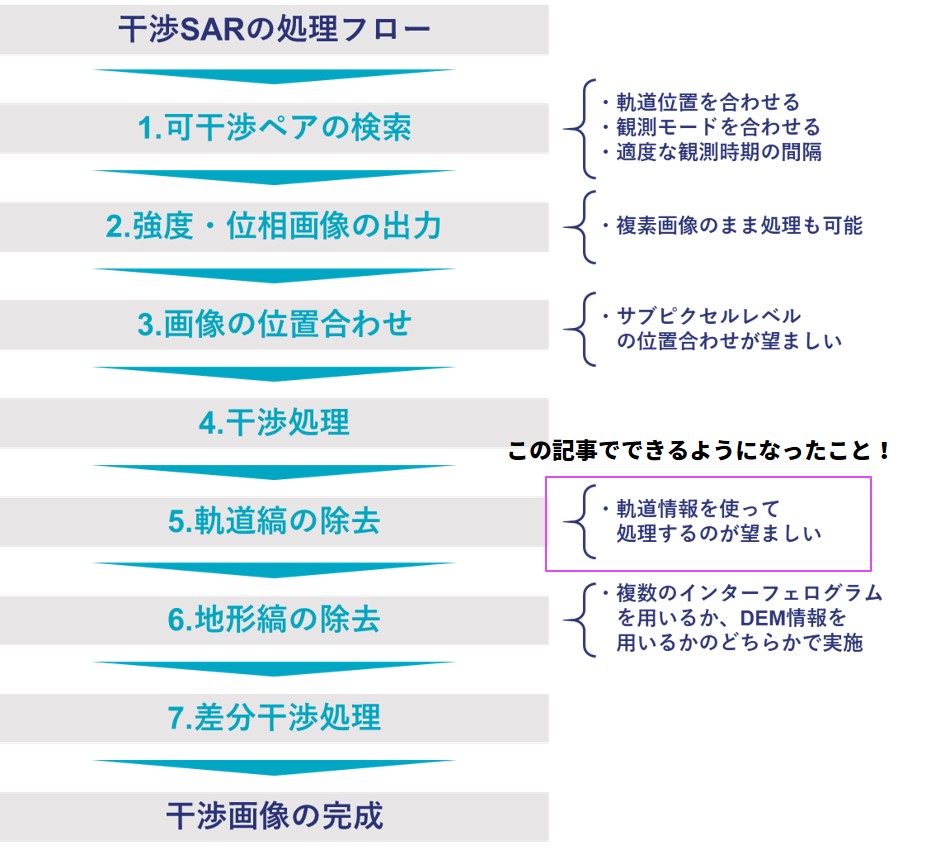
今後も、徐々に高度なアルゴリズムを紹介していく予定ですので、それを基にご自身でアップグレードさせていくことで、オリジナルの干渉SARアプリケーションを目指していただければと思います。ご拝読ありがとうございました。


