【コード付き】Tellusで干渉SARをやってみた(DEM編)
SARの有望な解析手法の一つである干渉SARを深堀していくシリーズ第三弾!いよいよ、標高モデルを使って地形縞の除去にチャレンジします。
記事作成時から、Tellusからデータを検索・取得するAPIが変更になっております。該当箇所のコードについては、以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/access/traveler_api_20220310_
firstpart.html
2022年8月31日以降、Tellus OSでのデータの閲覧方法など使い方が一部変更になっております。新しいTellus OSの基本操作は以下のリンクをご参照ください。
https://www.tellusxdp.com/ja/howtouse/tellus_os/start_tellus_os.html
宙畑では衛星データの一つであるSAR(サー)についてこれまでも詳しく取り上げてきました。
その中でも、干渉SARという解析手法は、地盤の沈下や隆起を把握することができ実ビジネスへの応用が様々考えられる技術です。
この連載では、SARの原理を深く知ってもらいたいとの思いから、干渉SARの解析手法を、Tellusで実装することを目標に、これまで必要なアルゴリズムをフルスクラッチで書いてきました。
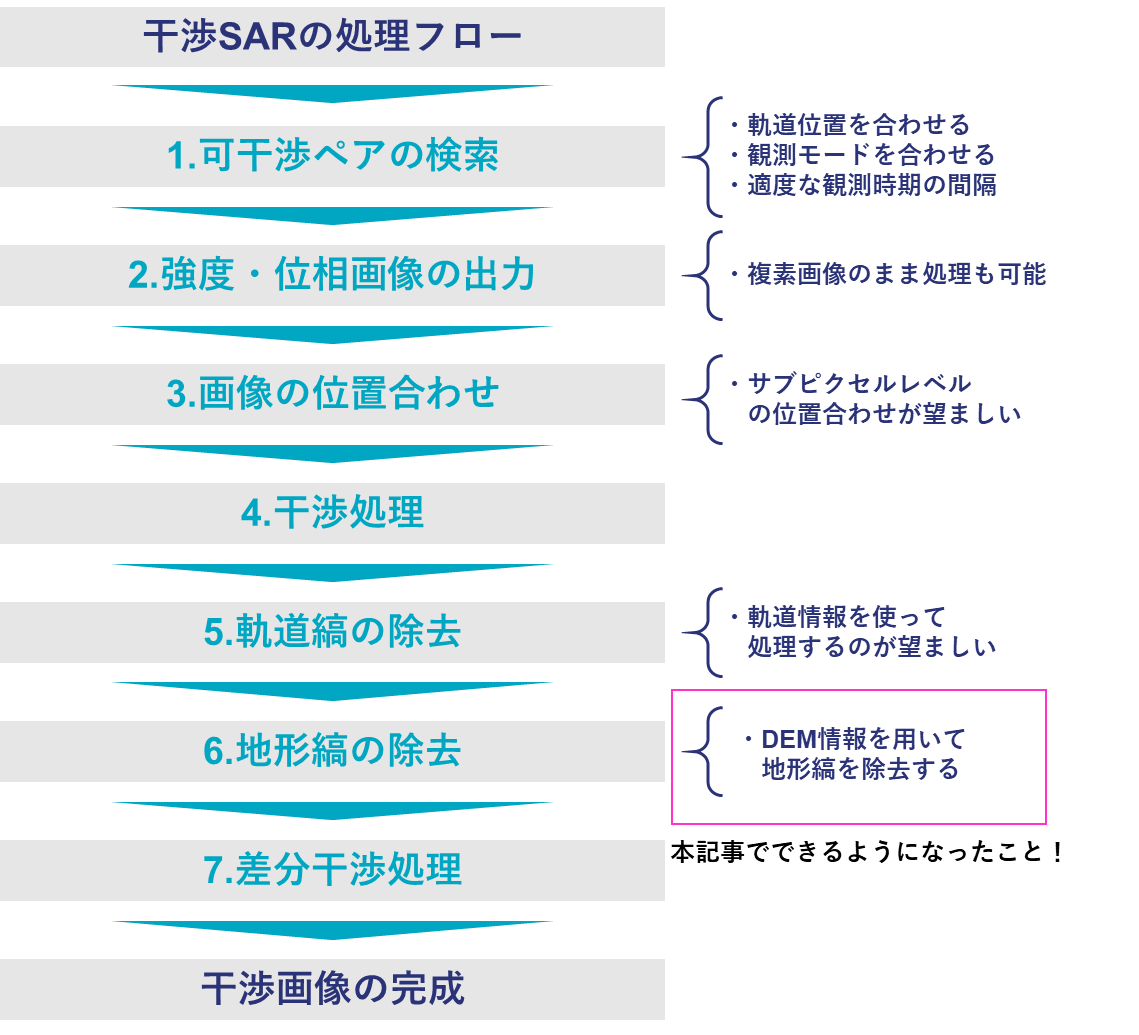
干渉SARの処理フローは以下の通りです。
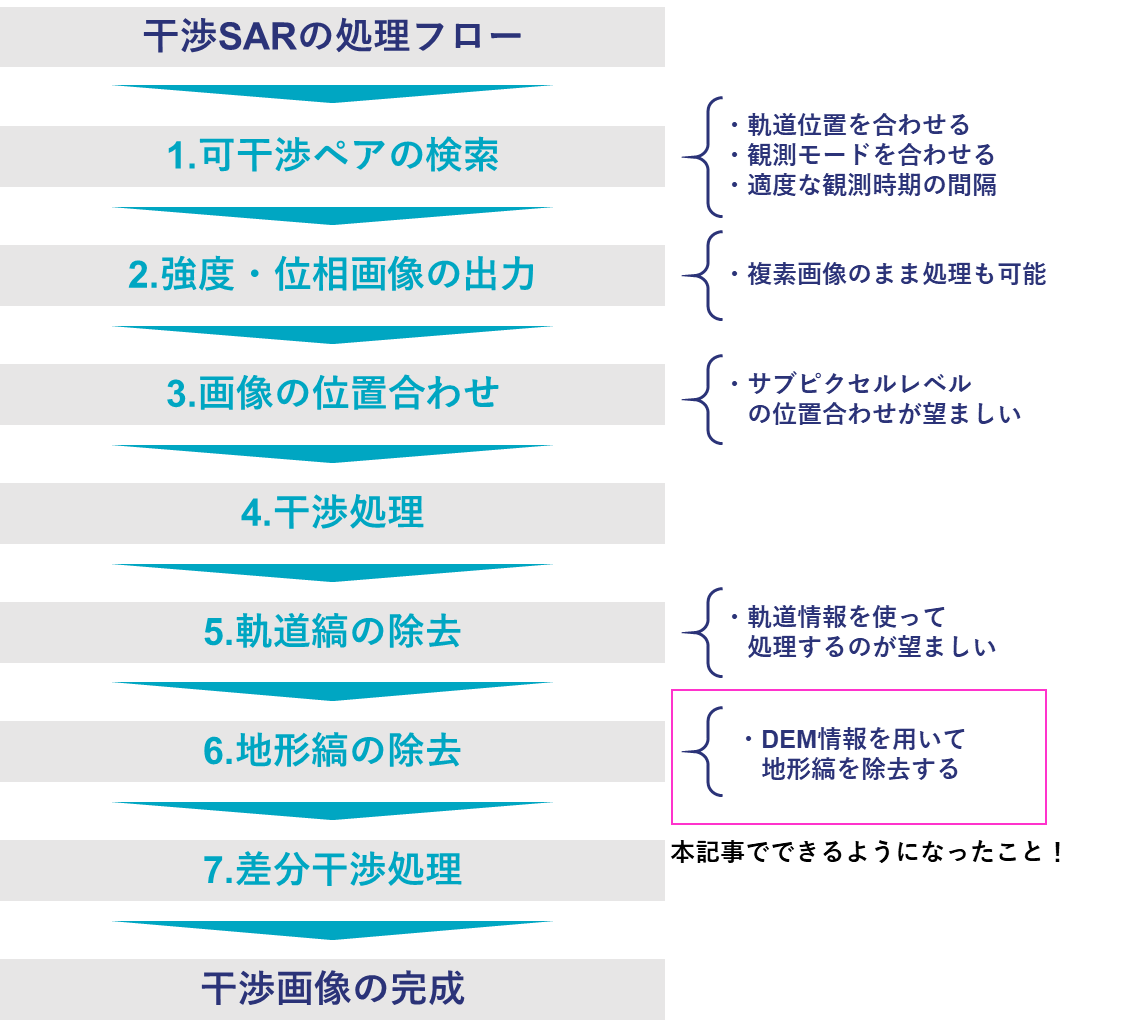
このフローの全体については以下の記事で解説していますので、まだご覧になっていない方はご覧ください。
【コード付き】地盤の沈降が分かる干渉SAR解析をTellusでやってみた
https://sorabatake.jp/12465/
また、フローの「5.軌道縞の除去」については、以下の記事にさらに詳しく取り上げています。
【コード付き】Tellusで干渉SARをやってみた(山編)
https://sorabatake.jp/15653/
本記事ではこの続編として、「6.地形縞の除去」について詳しく取り上げます。具体的には、DEM(標高情報)を用いて地形縞を除去する方法を紹介します。
この手法は、山などの起伏のある地形で干渉SARを行い、地震や劣化による地盤の変化を解析するために、必要となるアルゴリズムです。
本記事前半は、これまでの記事でもご紹介した内容をおさらいとして掲載しています。すでにご存じの方は、本記事の「メイントピック:DEMによる地形縞の除去」よりお読みください。
また、本記事で出てくるコードはGithubでも公開していますので、適宜ご参照ください。
干渉SARとは?
おさらいになりますが、干渉SARとは、一言でいえば、「電波の位相差を測ることで地表面の変化を知る技術」と言えます。衛星が同じ位置から電波を放射したとき、地表面が時期によって変化していれば、それが反射波の位相のずれとして検知されるので、地表面の変化を抽出することができるのです。
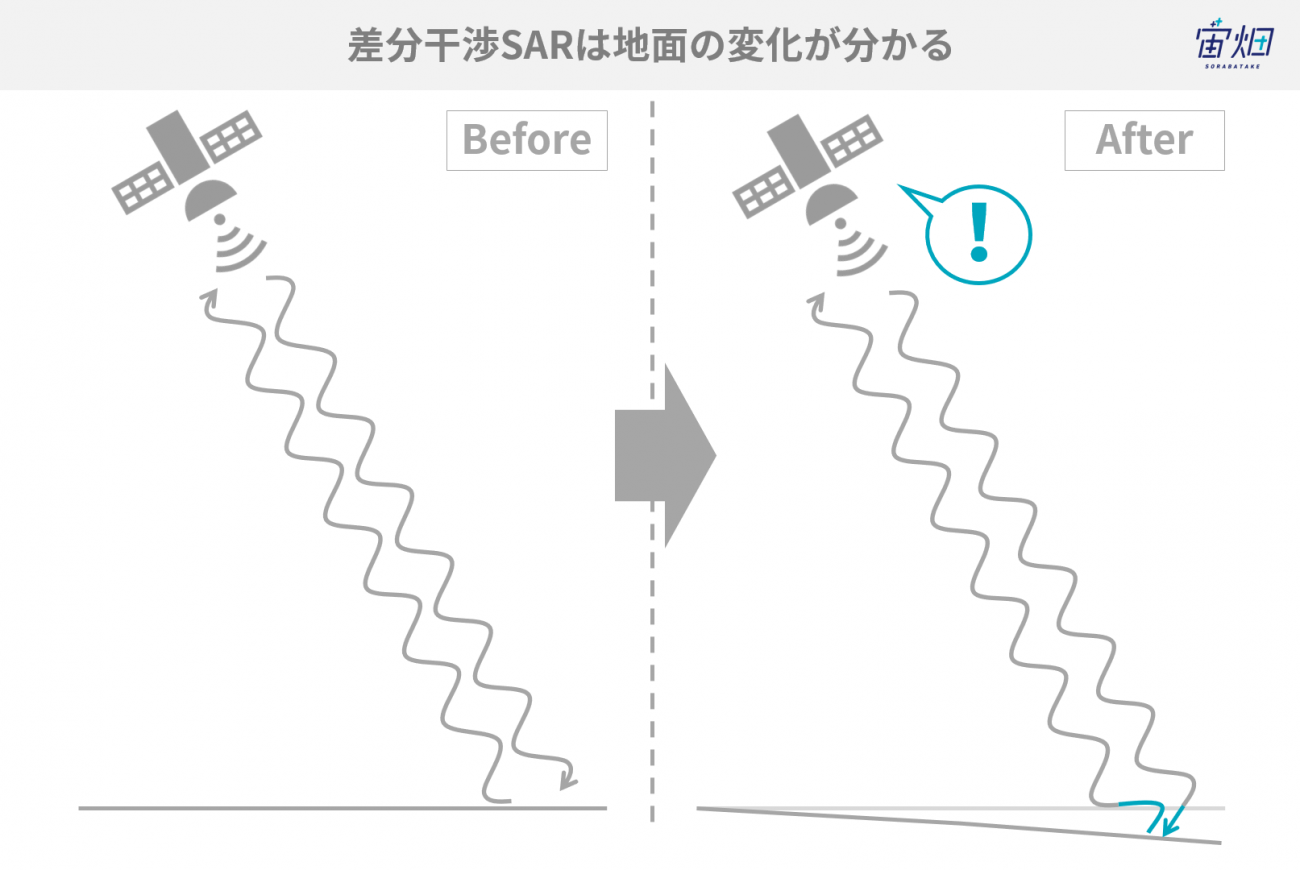
干渉SARの詳しい説明は以前に一般財団法人リモート・センシング技術センター(RESTEC)に解説していただいた記事がありますので、こちらを参照してください。
【干渉SAR(InSAR)とは-分かること、事例、仕組み、読み解き方-】
https://sorabatake.jp/4343/
干渉ペアをダウンロードする
2枚のSAR画像を干渉させるには、いくつか条件があることを以前の記事で説明しました。大事なことは、同じ軌道(位置・向き)から観測したものであること、同じ観測モードであること、そして、観測時期が離れすぎていないこと、の3点です。
ALOS-2の場合、ビーム番号、パス番号、フレーム番号、観測モードがすべて一致するプロダクトで干渉可能です。今回は、前回の記事でも使用した富士山周辺のシーンを使っていきます。
import os, requests
import numpy as np
TOKEN = "ご自身のトークンを入力してください"
def search_palsar2_l11(params={}, next_url=''):
if len(next_url) > 0:
url = next_url
else:
url = 'https://file.tellusxdp.com/api/v1/origin/search/palsar2-l11'
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url,params=params, headers=headers)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
return r.json()
def publish_palsar2_l11(dataset_id):
url = 'https://file.tellusxdp.com/api/v1/origin/publish/palsar2-l11/{}'.format(dataset_id)
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url, headers=headers)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
return r.json()
def download_file(url, dir, name):
headers = {
"Authorization": "Bearer " + TOKEN
}
r = requests.get(url, headers=headers, stream=True)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
if os.path.exists(dir) == False:
os.makedirs(dir)
with open(os.path.join(dir,name), "wb") as f:
for chunk in r.iter_content(chunk_size=1024):
f.write(chunk)
def main():
#富士山周辺の2シーンをダウンロード
dataset_id = ['ALOS2176170700-170827','ALOS2229990700-180826']
for i in range(2):
published = publish_palsar2_l11(dataset_id[i])
for file in published['files']:
file_name = file['file_name']
file_url = file['url']
#サムネイル画像、HH偏波の画像、サマリテキストファイル、リーダファイルのみをダウンロードします
if "jpg" in file_name or "IMG-HH" in file_name or "summary" in file_name or "LED" in file_name:
print(file_name)
file = download_file(file_url, dataset_id[i], file_name)
if __name__=="__main__":
main()
ダウンロードができたら、サムネイル画像が以下のものになっているかを確認して次に進んでください。

強度画像と位相画像を出力
それぞれのプロダクトから、強度画像と位相画像を出力します。シーン全体では、サイズが大きすぎてメモリエラーとなるため、範囲を指定して出力します。
また、解析のステップごとに、Numpy配列を出力・保存して、次のステップで読み込んで利用することで、ステップごとにコードを改良しやすいように工夫しています。また、記事中に一度記載した関数は、2度目以降は省略していきます。
import os
import numpy as np
import struct
import matplotlib.pyplot as plt
import math
from io import BytesIO
import cv2
def gen_img(fp,pl):
fp.seek(236)
nline = int(fp.read(8))
fp.seek(248)
ncell = int(fp.read(8))
nrec = 544 + ncell*8
nline = pl[3]-pl[2]
fp.seek(720)
fp.seek(int((nrec/4)*(pl[2])*4))
data = struct.unpack(">%s"%(int((nrec*nline)/4))+"f",fp.read(int(nrec*nline)))
data = np.array(data).reshape(-1,int(nrec/4))
data = data[:,int(544/4):]
data = data[:,::2] + 1j*data[:,1::2]
data = data[:,pl[0]:pl[1]]
sigma = 20*np.log10(abs(data)) - 83.0 - 32.0
phase = np.angle(data)
sigma = np.array(255*(sigma - np.amin(sigma))/(np.amax(sigma) - np.amin(sigma)),dtype="uint8")
sigma = cv2.equalizeHist(sigma)
return sigma, phase
def main():
dataset_id = ['ALOS2176170700-170827','ALOS2229990700-180826'] #Mt.Fuji
pl = [2050, 6150, 6450, 12750]
for i in range(2):
img = open(os.path.join(dataset_id[i],'IMG-HH-'+dataset_id[i]+'-HBQR1.1__A'),mode='rb')
sigma, phase = gen_img(img,pl)
np.save('sigma%02d.npy'%(i+1),sigma)
np.save('phase%02d.npy'%(i+1),phase)
plt.figure()
plt.imsave('sigma%02d.png'%(i+1), sigma,cmap='gray', vmin = 0, vmax = 255)
plt.imsave('phase%02d.png'%(i+1), phase,cmap='jet')
if __name__=="__main__":
main()
これによって得られた強度画像は以下の通りです。シーン1とシーン2はほぼ同じ画像なので、シーン1のみ表示します。強度画像は、反射係数を校正して対数化し、さらにOpenCVの機能を使って強度のヒストグラムを平坦化しています。そうすることで、ふたつのシーンの濃淡を合わせて、位置合わせがしやすくなります。また、この時点ではまだ位相はノイズと変わらない画像のため省略します。
位相情報が意味を持つのは、干渉解析など、他の画像との差分を抽出した時になります。しかし、正確に干渉させるためには、ふたつの画像の位置をピッタリ合わせる必要があるので、その位置合わせを行うために強度画像が必要、ということを理解しておいていただければと思います。

干渉処理
SAR画像を干渉させるとは、一言でいえば「強度画像で位置を合わせて、位相画像の差分を取ること」です。この処理も、基本的に前回のコードとほぼ同じです。以下のコードをそのまま実行すれば、干渉させた位相画像が得られます。
#画像の位置合わせを行う関数
def coregistration(A,B,C,D):
py = len(A)
px = len(A[0])
A = np.float64(A)
B = np.float64(B)
d, etc = cv2.phaseCorrelate(B,A)
dx, dy = d
if dx >= 0 and dy >= 0:
dx = int(np.round(dx))
dy = int(np.round(dy))
rD = D[0:py-dy,0:px-dx]
rC = C[dy:py,dx:px]
elif dx = 0:
dx = int(np.round(dx))
dy = int(np.round(dy))
rD = D[0:py-dy,abs(dx):px]
rC = C[dy:py,0:px-abs(dx)]
return rC, rD
def wraptopi(x):
x = x - np.floor(x/(2*np.pi))*2*np.pi - np.pi
return x
def main():
phase01 = np.load('phase01.npy')
sigma01 = np.load('sigma01.npy')
phase02 = np.load('phase02.npy')
sigma02 = np.load('sigma02.npy')
coreg_phase01, coreg_phase02 = coregistration(sigma01,sigma02,phase01,phase02)
ifgm = wraptopi(coreg_phase01 - coreg_phase02)
np.save('ifgm.npy',ifgm)
plt.figure()
plt.imsave('ifgm.png', ifgm, cmap = "jet")
if __name__=="__main__":
main()これによって出力された干渉画像(インターフェログラム)は以下の通りです。中央に富士山の山頂らしきものは判別できますが、縞模様が多すぎてほとんど何も判別できません。この干渉画像には、軌道縞(衛星の軌道のずれによる縞)と地形縞(地形の起伏に起因する縞)が混在しています。

ここではまず、前回の記事で紹介したアルゴリズムで、軌道縞を除去していきます。そしてそのあと、本記事のメイントピックである「DEMによる地形縞の除去」を実施してみたいと思います。
軌道情報を使って軌道縞を除去する
軌道縞とは、2回の観測時の衛星の位置が違うことによって生じる縞模様です。図で表すと以下のようになります。
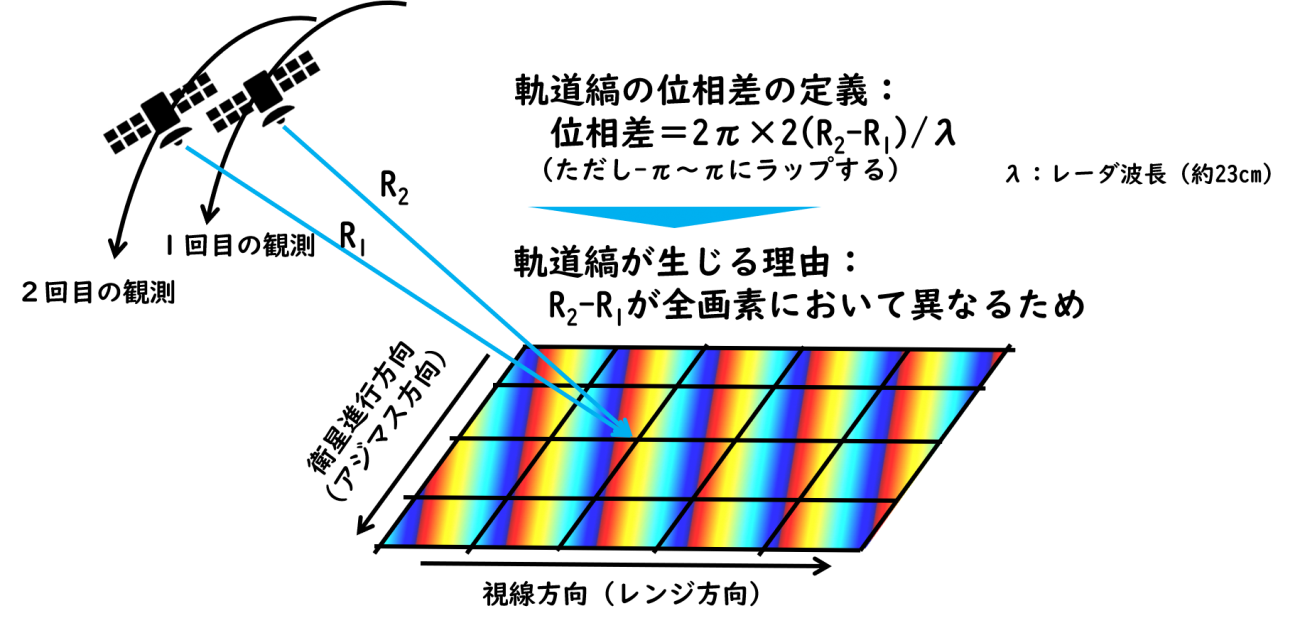
※ラップ:この式だと結果が-πより小さくなったり、πより大きくなったりするので、
それを[-π~+π]に戻す処理を言います
また、実際にはSAR画像は10秒くらいの時間をかけて画像1枚分のエリアを観測しています。その10秒間で衛星は100km程度移動していますので、その移動分を無視することはできません。そこで、画像の各画素が取得された時の衛星の位置を特定するため、観測中の衛星の位置と時刻を記録したデータを用いて、適切に補間していきます。
実際のアルゴリズムは、CEOSフォーマットを読み込む非常に難解なものなので、コードをすべて理解する必要はありません。上記の説明が理解できれば、以下のコードをそのまま実行してみてください。今回は画像サイズが大きいため、10分ほどかかります。
import scipy
from scipy.interpolate import interp1d
#観測中の衛星位置を出力する関数
def get_sat_pos(led,img):
img.seek(720+44)
time_start = struct.unpack(">i",img.read(4))[0]/1000
led.seek(720+500)
lam = float(led.read(16)) #m
led.seek(720+4096+140)
position_num = int(led.read(4))
led.seek(720+4096+182)
time_interval = int(float(led.read(22)))
led.seek(720+4096+160)
start_time = float(led.read(22))
led.seek(720+68)
center_time = led.read(32)
Hr = float(center_time[8:10])*3600
Min = float(center_time[10:12])*60
Sec = float(center_time[12:14])
msec = float(center_time[14:17])*1e-3
center_time = Hr+Min+Sec+msec;
time_end = time_start + (center_time - time_start)*2;
img.seek(236)
nline = int(img.read(8))
time_obs = np.arange(time_start, time_end, (time_end - time_start)/nline)
time_pos = np.arange(start_time, start_time+time_interval*position_num,time_interval)
pos_ary = [];
led.seek(720+4096+386)
for i in range(position_num):
for j in range(3):
pos = float(led.read(22))
pos_ary.append(pos)
led.read(66)
pos_ary = np.array(pos_ary).reshape(-1,3)
fx = scipy.interpolate.interp1d(time_pos,pos_ary[:,0],kind="cubic")
fy = scipy.interpolate.interp1d(time_pos,pos_ary[:,1],kind="cubic")
fz = scipy.interpolate.interp1d(time_pos,pos_ary[:,2],kind="cubic")
X = fx(time_obs)
Y = fy(time_obs)
Z = fz(time_obs)
XYZ = np.zeros(nline*3).reshape(-1,3)
XYZ[:,0] = X
XYZ[:,1] = Y
XYZ[:,2] = Z
return XYZ
#軌道縞を生成する関数
def get_orbit_stripe(pos1,pos2,pl,led):
led.seek(720+500)
lam = float(led.read(16)) # [m]
a = []
b = []
c = []
led.seek(720+4096+1620+4680+16384+9860+325000+511000+3072+728000+1024)
for i in range(25):
a.append(float(led.read(20)))
for i in range(25):
b.append(float(led.read(20)))
for i in range(2):
c.append(float(led.read(20)))
npix = pl[1]-pl[0]
nline = pl[3]-pl[2]
orb = np.zeros((nline,npix))
for i in range(npix):
for j in range(nline):
px = i+pl[0]-c[0]
ln = j+pl[2]-c[1]
ilat = (a[0]*ln**4 + a[1]*ln**3 + a[2]*ln**2 + a[3]*ln + a[4])*px**4 + (a[5]*ln**4 + a[6]*ln**3 + a[7]*ln**2 + a[8]*ln + a[9])*px**3 + (a[10]*ln**4 + a[11]*ln**3 + a[12]*ln**2 + a[13]*ln + a[14])*px**2 + (a[15]*ln**4 + a[16]*ln**3 + a[17]*ln**2 + a[18]*ln + a[19])*px + a[20]*ln**4 + a[21]*ln**3 + a[22]*ln**2 + a[23]*ln + a[24]
ilon = (b[0]*ln**4 + b[1]*ln**3 + b[2]*ln**2 + b[3]*ln + b[4])*px**4 + (b[5]*ln**4 + b[6]*ln**3 + b[7]*ln**2 + b[8]*ln + b[9])*px**3 + (b[10]*ln**4 + b[11]*ln**3 + b[12]*ln**2 + b[13]*ln + b[14])*px**2 + (b[15]*ln**4 + b[16]*ln**3 + b[17]*ln**2 + b[18]*ln + b[19])*px + b[20]*ln**4 + b[21]*ln**3 + b[22]*ln**2 + b[23]*ln + b[24]
ixyz = lla2ecef(ilat*np.pi/180.0,ilon*np.pi/180.0,0)
r1 = np.linalg.norm(pos1[j+pl[2],:] - ixyz);
r2 = np.linalg.norm(pos2[j+pl[2],:] - ixyz);
orb[j,i] = wraptopi(2*np.pi/lam*2*(r2-r1));
return orb
#緯度経度高度から地球のECEF座標系のXYZを出力する関数
def lla2ecef(lat,lon,alt):
a = 6378137.0
f = 1 / 298.257223563
e2 = 1 - (1 - f) * (1 - f)
v = a / math.sqrt(1 - e2 * math.sin(lat) * math.sin(lat))
x = (v + alt) * math.cos(lat) * math.cos(lon)
y = (v + alt) * math.cos(lat) * math.sin(lon)
z = (v * (1 - e2) + alt) * math.sin(lat)
return np.array([x,y,z])
def main():
dataset_id = 'ALOS2176170700-170827' #Mt.Fuji
fpimg = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-HBQR1.1__A'),mode='rb')
fpled = open(os.path.join(dataset_id,'LED-'+dataset_id+'-HBQR1.1__A'),mode='rb')
pos1 = get_sat_pos(fpled,fpimg)
dataset_id = 'ALOS2229990700-180826' #Mt.Fuji
fpimg = open(os.path.join(dataset_id,'IMG-HH-'+dataset_id+'-HBQR1.1__A'),mode='rb')
fpled = open(os.path.join(dataset_id,'LED-'+dataset_id+'-HBQR1.1__A'),mode='rb')
pos2 = get_sat_pos(fpled,fpimg)
pl = [2050, 6150, 6450, 12750]
orbit_stripe = get_orbit_stripe(pos1,pos2,pl,fpled)
np.save('orbit_stripe.npy',orbit_stripe)
plt.figure()
plt.imsave('orbit_stripe.png', orbit_stripe, cmap = "jet")
if __name__=="__main__":
main()
得られた軌道縞は以下の図の通りです。干渉画像に対して、軌道縞だけをまずは除去するため、ここでは地球を起伏の無い楕円球体であると仮定して、軌道縞をシミュレートしています。

次に、この軌道縞を干渉画像から差し引いて、軌道縞を除去します。
def main():
ifgm = np.load('ifgm.npy')
orbit_stripe = np.load('orbit_stripe.npy')
#軌道縞の画像サイズをインターフェログラムのサイズと合わせます
orbit_stripe = orbit_stripe[0:ifgm.shape[0],0:ifgm.shape[1]]
ifgm_sub_orb = wraptopi(ifgm - orbit_stripe) #軌道縞除去の処理
np.save('ifgm_sub_orb.npy',ifgm_sub_orb)
plt.figure()
plt.imsave('ifgm_sub_orb.png', ifgm_sub_orb, cmap = "hsv")
if __name__=="__main__":
main()
得られた画像は以下の通りです(強度画像と重ね合わせています)。かなりキレイに軌道縞が取り除けていることがわかります。その証拠に、山頂を中心に等高線のように縞模様が分布しています。この残った縞模様が、地形の起伏に起因する地形縞となります。

ではここからが本記事のメイントピックとなる、DEMを用いた地形縞の除去について、説明していきます。
本記事のメイントピック:DEMによる地形縞の除去
DEMとは、Digital Elevation Modelの略で、日本語では「数値標高モデル」と呼ばれています。つまり、標高を含んだ地図情報です。日本のDEMについては、国土地理院が整備している基盤地図情報数値標高モデル、JAXAが衛星画像を基に作成したAW3D、NASAのスペースシャトルによって観測されたSRTMなどが無料で公開されています。それぞれ精度や観測時期、データのフォーマットなどが異なりますので、必要に応じて使い分けます。
◇国土地理院
特徴:5m~10mと比較的解像度が高い。航空機によって測量されたデータ。
リンク:https://fgd.gsi.go.jp/download/ref_dem.html
JAXA AW3D30
特徴:JAXAの衛星ALOSに搭載された光学立体視センサPRISMによって観測されたモデル。30mの解像度(標高の精度は約5m)で地球の陸域全体がカバーされている。
リンク:https://www.eorc.jaxa.jp/ALOS/aw3d30/index_j.htm
※Tellus上でもAPIが公開されています
ASTER GDEM
特徴:経産省が開発したASTERセンサによって観測されたモデル。30mの解像度(標高の精度は約7~14m)で地球の陸域全体がカバーされている。
リンク:https://ssl.jspacesystems.or.jp/ersdac/GDEM/J/
※Tellus上でもAPIが公開されています
NASA SRTM
特徴:30mか90mの解像度。船外アンテナを用いたSARによる観測。
リンク:https://www2.jpl.nasa.gov/srtm/
今回は、JAXAが公開しているAW3D30を使用します。上記のリンク先から、ユーザー登録をしてダウンロードページに進んでください。なお、今回掲載するコードでは、特定のDEMデータに最適化・自動化したものではないため、配列の形式さえ揃っていれば、解像度の異なるどんなDEMでも処理は可能です。
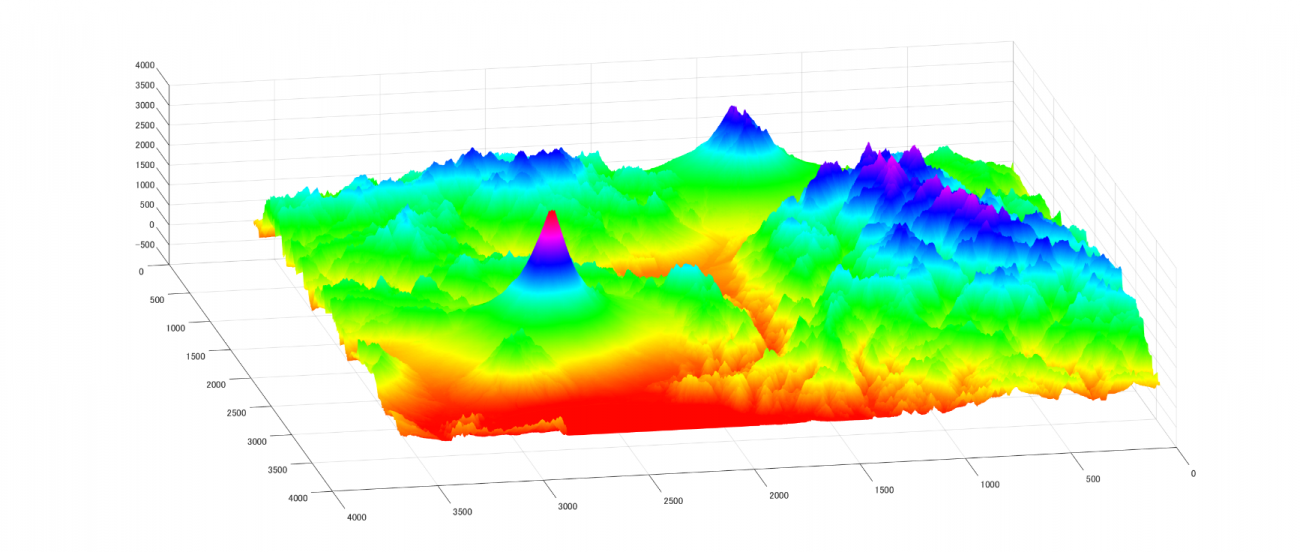
AW3D30は緯度経度1度ごとに分けられた「タイル」で用意されています。今回は富士山を含んだエリアのDEMですので、北緯35度、東経138度のエリアをダウンロードします。
ダウンロードができたら、フォルダ内の「ALPSMLC30_N035E138_DSM.tif」をTellusの開発環境にアップロードしてください。3Dグラフで表示するとこのようになります。
Credit : JAXA
AW3D30は、緯度によって空間の解像度が異なるのですが、0~60度の範囲であれば、緯度方向も経度方向も1秒角刻みです。3600秒角が1度ですから、1タイル(緯度1度×経度1度)あたり3600×3600の解像度を持つデータということになります。
それでは、このDEMを使って、先ほどの干渉画像から地形縞を除去するには、どのようにしたらよいでしょうか?大きくは以下の三つのステップになります。
①DEMを干渉画像に合わせてカット・回転させ、干渉画像にフィットさせる
②軌道縞と同じ要領で、衛星の軌道を模擬して地形縞をシミュレートする
③干渉画像と同じになるように幾何補正・解像度を合わせてリサンプリングする
この各ステップで、いかに誤差を抑え、自動化するかが、最終的なアプリケーションにおいては極めて重要ですが、ここではあえてそのような高度な手法は用いず、原始的ですがわかりやすい手順で進めていきたいと思います。(①~③の順番は部分的に前後します)
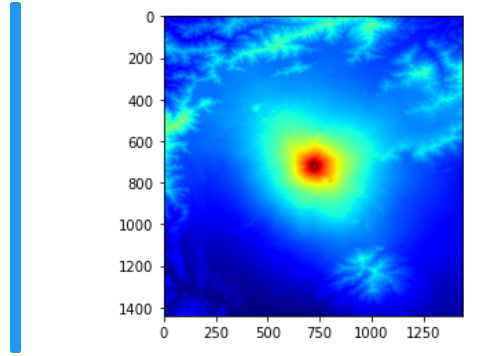
ではまず、富士山を中心に、DEMを適当な大きさにカットします。ここで、あとで画像を回転させることを考えて、少し大きめにカットしておきます。
import os
import numpy as np
import matplotlib.pyplot as plt
import cv2
import math
from osgeo import gdal, gdalconst, gdal_array
def main():
tif = gdal.Open('ALPSMLC30_N035E138_DSM.tif', gdalconst.GA_ReadOnly)
dem = tif.GetRasterBand(1).ReadAsArray(0,0,3600,3600)
N = 35#DEMの北緯
E = 138#DEMの東経
P = 3600#DEMのピクセル数
lat = np.linspace(N+1,N,P);
lon = np.linspace(E,E+1,P);
latlon = [35.163, 35.563, 138.530, 138.930]#富士山山頂を中心とした±0.2度のLat/Lon
top_lat = int(np.fix(P-(latlon[1]-N)*P))
bottom_lat = int(np.fix(P-(latlon[0]-N)*P))
left_lon = int(np.fix((latlon[2]-E)*P)-1)
right_lon = int(np.fix((latlon[3]-E)*P))
#上記の情報を使ってDEMをカットする
dem = dem[top_lat:bottom_lat,left_lon:right_lon]
lat = lat[top_lat:bottom_lat]
lon = lon[left_lon:right_lon]
np.save('dem_cut.npy',dem)
np.save('lat.npy',lat)
np.save('lon.npy',lon)
plt.imshow(dem, cmap = "jet", clim = [0,3771])
plt.imsave('dem_cut.png', dem, cmap = "hsv")
if __name__=="__main__":
main()
実行結果は以下の通りです。中央の赤くなっている標高の高い部分が富士山です。
次に、軌道縞と同じように、衛星の軌道情報を使って、地形縞をシミュレートします。やり方は軌道縞の時とほとんど同じですが、今回は、アルゴリズムの簡素化と、計算量の節約のために、衛星の位置はシーンセンタの座標として固定します。
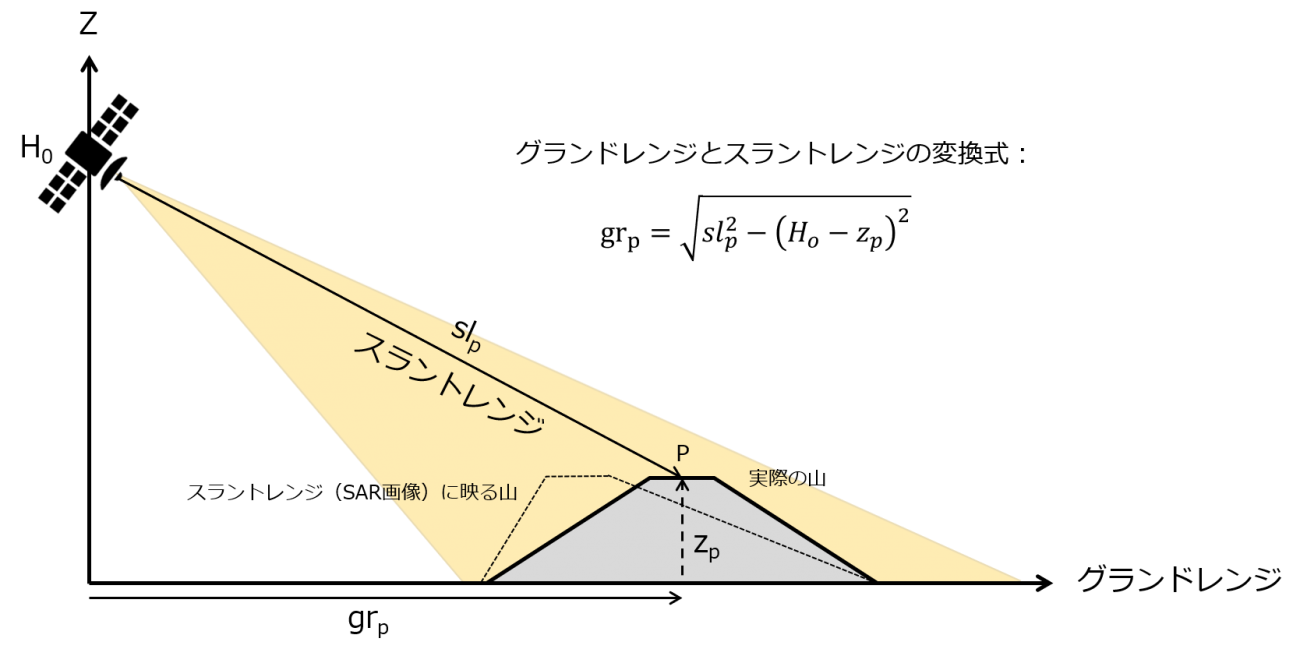
また、DEMを干渉画像へ重ね合わせるためには、幾何補正が必要になります。下図に示すように、幾何補正前のSAR画像は、SARから見て手前にある山腹が倒れこんでいるように画像化されています。それは、送受信されている電波の経路が、山の標高分短くなるためです。
これは、簡単な三平方の定理を使って、地平面上の距離(グランドレンジ)と、電波の経路(スラントレンジ)の座標変換を行うことで、幾何補正をすることができます。これを行うために、次のコード内で、衛星と各観測点との距離(スラントレンジ)をリスト化しておきます。DEMは元々グランドレンジ上に等間隔に保存されているので、これらを用いて変換が可能になります。実際の幾何補正は後ほど行います。
import os
import numpy as np
import matplotlib.pyplot as plt
import cv2
import math
def main():
dem = np.load('dem_cut.npy')
lat = np.load('lat.npy')
lon = np.load('lon.npy')
#衛星座標(シーンセンタ固定※軌道縞を作成したコードから抽出しています)
satpos0c = [-4078.581984e3, 4081.311933e3, 3974.603863e3]
satpos1c = [-4078.383306e3, 4081.518669e3, 3974.563115e3]
Fc = 1257.5e6
CVEL = 3e8
lam = CVEL/Fc
geo_resample = np.zeros(np.shape(dem)) #幾何補正パラメータ
terrain_stripe = np.zeros(np.shape(dem)) #地形縞シミュレート
for i in range(len(lat)):
if i % 100 == 0:
print(i,len(lat))
for j in range(len(lon)):
ixyz = lla2ecef(np.deg2rad(lat[i]),np.deg2rad(lon[j]),dem[i,j]+50.0) #DEMの座標(50mはジオイド高)
fxyz = lla2ecef(np.deg2rad(lat[i]),np.deg2rad(lon[j]),50.0) #楕円球体の座標
r0 = np.linalg.norm(satpos0c - ixyz)
r1 = np.linalg.norm(satpos1c - ixyz)
f0 = np.linalg.norm(satpos0c - fxyz)
f1 = np.linalg.norm(satpos1c - fxyz)
terrain_stripe[i,j] = wraptopi(4*np.pi/lam*4*(r1-r0-(f1-f0)))
geo_resample[i,j] = r0
geo_resample[i,:] = (geo_resample[i,:]-min(geo_resample[i,:]))/(max(geo_resample[i,:])-min(geo_resample[i,:]))
np.save('geo_resample.npy',geo_resample)
np.save('terrain_stripe.npy',terrain_stripe)
plt.imsave('terrain_stripe.png', terrain_stripe, cmap = "hsv")
if __name__=="__main__":
main()
ここで得られた地形縞のシミュレート結果は以下の通りです。この図と、先ほど作った干渉画像(下図(右))を見比べてみるとわかるように、このシミュレートした地形縞は、富士山を真上から見たような図になっています。一方で右の干渉画像は、富士山を斜めから見たような縞模様になっています。この違いが、先ほどの図で示した、グランドレンジ(DEM)、スラントレンジ(干渉画像)の違いであると言えます。

では次に、この画像をさらに加工していきます。次の工程では、一気に地形縞を干渉画像にフィットさせていきます。まず、①地形縞を回転させ、干渉画像と同じ角度に直します。今回は、配列を90度回転させた後、さらに10度時計回りに回転させます。次に、②先ほど作った幾何補正用の配列を使って、地形縞をリサンプリングします。これで、DEMによる地形縞が斜めから見たような図になります。最後に、③干渉画像と照らし合わせて、縦横にフィットするようカットします。ここでは、目視でフィッティングさせた結果を用いています。
import os
import numpy as np
import matplotlib.pyplot as plt
import cv2
import math
from scipy import interpolate
def main():
terrain = np.load('terrain_stripe.npy')
terrain = np.rot90(terrain,-1)#干渉画像と向きを合わせるため90度行列を回転
#①地形縞の回転
center = (int(terrain.shape[1]/2),int(terrain.shape[0]/2))
angle = -10.0
trans = cv2.getRotationMatrix2D(center, angle, 1.0) #時計回りに10度回転
terrain_rot = cv2.warpAffine(terrain, trans, (terrain.shape[1],terrain.shape[0]))
plt.imsave('terrain_rot.png', terrain_rot, cmap = "hsv")
resample = np.load('geo_resample.npy')
resample = np.rot90(resample,-1)
#②幾何補正
for i in range(np.shape(resample)[1]):
f = interpolate.interp1d(resample[:,i],terrain_rot[:,i])
terrain_rot[:,i] = f(np.linspace(0,1,np.shape(resample)[0]))
plt.imsave('terrain_geo.png', terrain_rot, cmap = "hsv")
#③干渉画像にフィットするようにカット
dem = terrain_rot[150:980,435:1065]
np.save('dem_fit.npy',dem)
plt.imsave('dem_fit.png', dem, cmap = "hsv")
if __name__=="__main__":
main()
実行結果が下図になります。

ここで、フィッティングした画像が、干渉画像と重なっているかを確認してみます。簡易的なフィッティングではありますが、それなりに一致していることがわかります。

では、最後の加工として、DEMからシミュレートした地形縞の解像度を補間します。この時点では、まだAW3D30の30m分解能のままなので、これを干渉画像と全く同じ解像度になるよう、リサンプリングを行います。ここでは、一般的な補間処理の手法として、平面上の近傍にある既知の4点から補間を行う、バイリニア補間法を用います。出力される画像の見た目は前の画像と変わらないので省略します。処理には10分ほど時間を要します。
import os
import numpy as np
import matplotlib.pyplot as plt
import cv2
import math
def main():
dem = np.load('dem_fit.npy')
ifgm = np.load('ifgm_sub_orb.npy')
ifgm = np.fliplr(np.rot90(ifgm,-1))
NY = np.shape(ifgm)[0];
NX = np.shape(ifgm)[1];
posY = np.linspace(1,np.shape(dem)[0]-1,NY);
posX = np.linspace(1,np.shape(dem)[1]-1,NX);
#解像度のリサンプリング(バイリニア補間)
dem_res = np.zeros([NY,NX]);
for i in range(NY):
iy = int(np.fix(posY[i]))
dy = posY[i]-iy
for j in range(NX):
ix = int(np.fix(posX[j]))
dx = posX[j]-ix
dem_res[i,j] = (1-dx)*(1-dy)*dem[iy-1,ix-1]+dx*(1-dy)*dem[iy-1,ix]+(1-dx)*dy*dem[iy,ix-1]+dy*dx*dem[iy,ix]
np.save('dem_res.npy',dem_res)
plt.imsave('dem_res.png', dem_res, cmap = "hsv")
if __name__=="__main__":
main()
地形縞を除去してみよう!
これでようやく、干渉画像からDEMを用いて地形縞を除去する準備が整いました。軌道縞を除去した時と同様、最後は非常に簡単な処理になります。
import os
import numpy as np
import matplotlib.pyplot as plt
import cv2
import math
def main():
ifgm = np.load('ifgm_sub_orb.npy')
ifgm = np.fliplr(np.rot90(ifgm,-1))
plt.imsave('ifgm_fliplr.png', ifgm, cmap = "hsv")
dem = np.load('dem_res.npy')
#干渉画像から地形縞を除去する
ifgm_sub_dem = wraptopi(ifgm - dem)
np.save('ifgm_sub_dem.npy',ifgm_sub_dem)
plt.imsave('ifgm_sub_dem.png', ifgm_sub_dem, cmap = "hsv")
if __name__=="__main__":
main()それでは、地形縞を除去した干渉画像の出力結果をご覧ください。

この画像からどのようなことがわかるでしょうか?まず全体を見て、富士山の等高線に相当していた縞模様はある程度なくなっており、完全ではありませんが地形縞を取り除くことができたと言ってよいと思います。(よく見ると細い筋のような線が残ってしまっていますが、これは途中で回転・補間をした際に、縞の切れ目が上手く処理できていないためです)
また、山腹から離れた平野(画像左上部分)では、縞模様がほとんど見られないことから、軌道縞・地形縞の両方が正しく除去できていると言うことができると思います。
しかしながら、山腹にある局所的な凸凹地形に対して、はっきりした縞模様が残っています。この辺りは、やはり位置合わせが厳密に上手くいっていないことを表しており、今回の手法では十分な精度であるとは言えないと思われます。
この干渉画像が、仮に軌道縞と地形縞を正しく除去できていたとすると、残った縞模様は、観測した二時期の「差分」である、ということができます。今回の場合、2017年8月と2018年8月の差分になります。その差分の主成分は、二時期の間での地面の変位であり、1周期は1波長(約23cm)に相当します。ただし、この変位は、衛星の視線方向(スラントレンジ方向)に対する変位であるため、地面に垂直な変位成分を取り出すには、ここから更に幾何補正をかけていく必要があります。
しかしながら、これで干渉SARに必要な干渉処理と干渉縞(軌道縞と地形縞)の除去については、基本的な手順をすべてクリアしたと言ってよいでしょう。
まとめ
干渉SARの処理フローを再掲しておきます。今回は、DEMを用いて地形縞を除去することを新しく紹介しました。今回はかなりアナログな操作もありましたので、そういったところを自動化したり、高精度化させることで、より実用的なアプリケーションにすることが可能です。
現在、国内外で新しいSAR衛星が続々と打ち上げられており、SAR画像を解析する需要はますます高まりつつあります。Tellusを活用して、様々な解析にチャレンジしてみてはいかがでしょうか。ご読了ありがとうございました。
本記事で出てくるコードはGithubでも公開していますので、適宜ご参照ください。


