近年、自然災害が激甚化しており、洪水被害の報道が増えたと感じている方も多いのではないでしょうか？

実際に、全国の1時間降水量50mm以上の年間の発生回数は増えており、各地で対策が求められています。

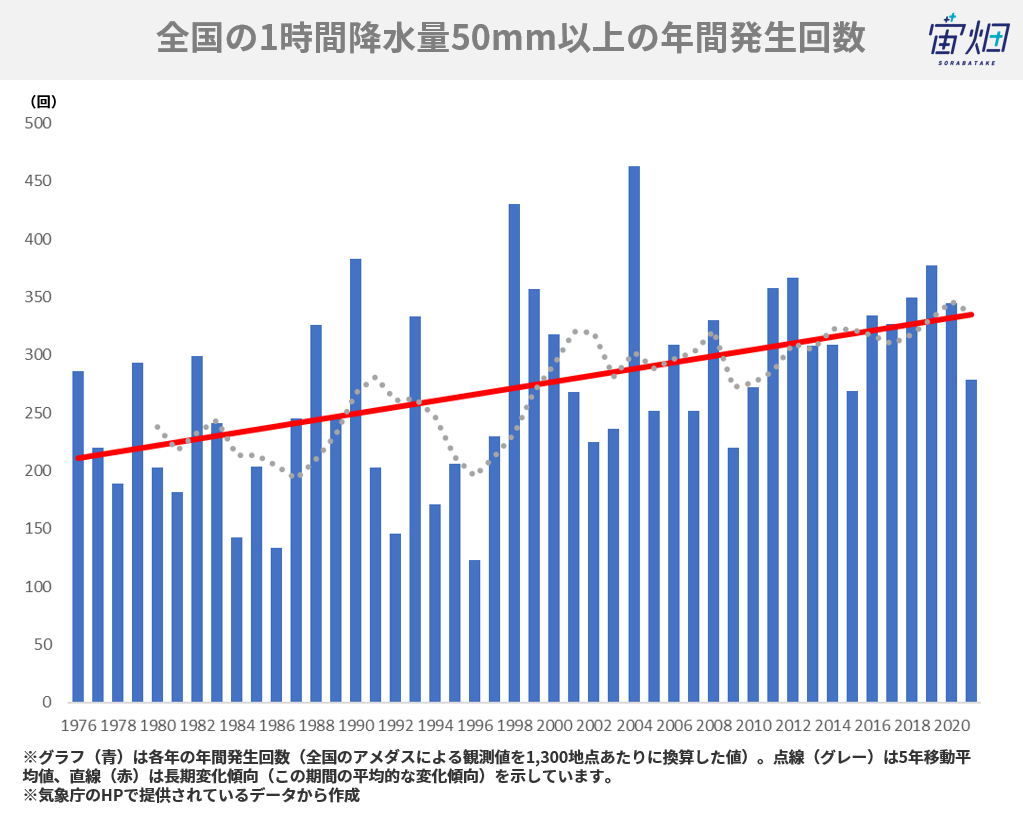
自然災害の激甚化は、これまで洪水被害にあっていなかった場所にも大きな被害をもたらしてしまうかもしれません。

現在、衛星データを活用した浸水深予測のソリューションが保険会社や地方自治体に導入され始めていますが、これまで一度も浸水被害が無かった場所の浸水深予測を行う場合は、当たり前ですが教師データがありません。

では、そのような場合にどのようにして被害が起きた場所の浸水深予測をするとよいのか。本記事では先にシミュレーションデータを作って、教師データとすればよいのではないかというアプローチから衛星データの解析までをコードと合わせて紹介しています。

ぜひ、読者の皆さんが住んでいる土地でもコードを動かしてみてください。

水害時の衛星データ

冒頭で紹介したように、水害時に衛星データを確認するということは近年増えています。被災に遭われた地域を衛星が撮像することで現地に行かなくても、その場の情報を得られる手段として衛星データが有効だからです。

特に、被災地は危険な場合が多く、現地で確かめることが難しい時には有効とされています。災害時のデータに以下の記事が詳しいです。

しかしながら、上述のように、全ての地域が被害にあったことがある訳ではありません。さらには、実際に撮像タイミングが合わず正確な被害状況のデータと衛星データがすべてのケースで揃っていることはなく、解析や予測を行うのを難航させています。特にディープラーニングのようなデータを必要とする分野では課題の１つです。

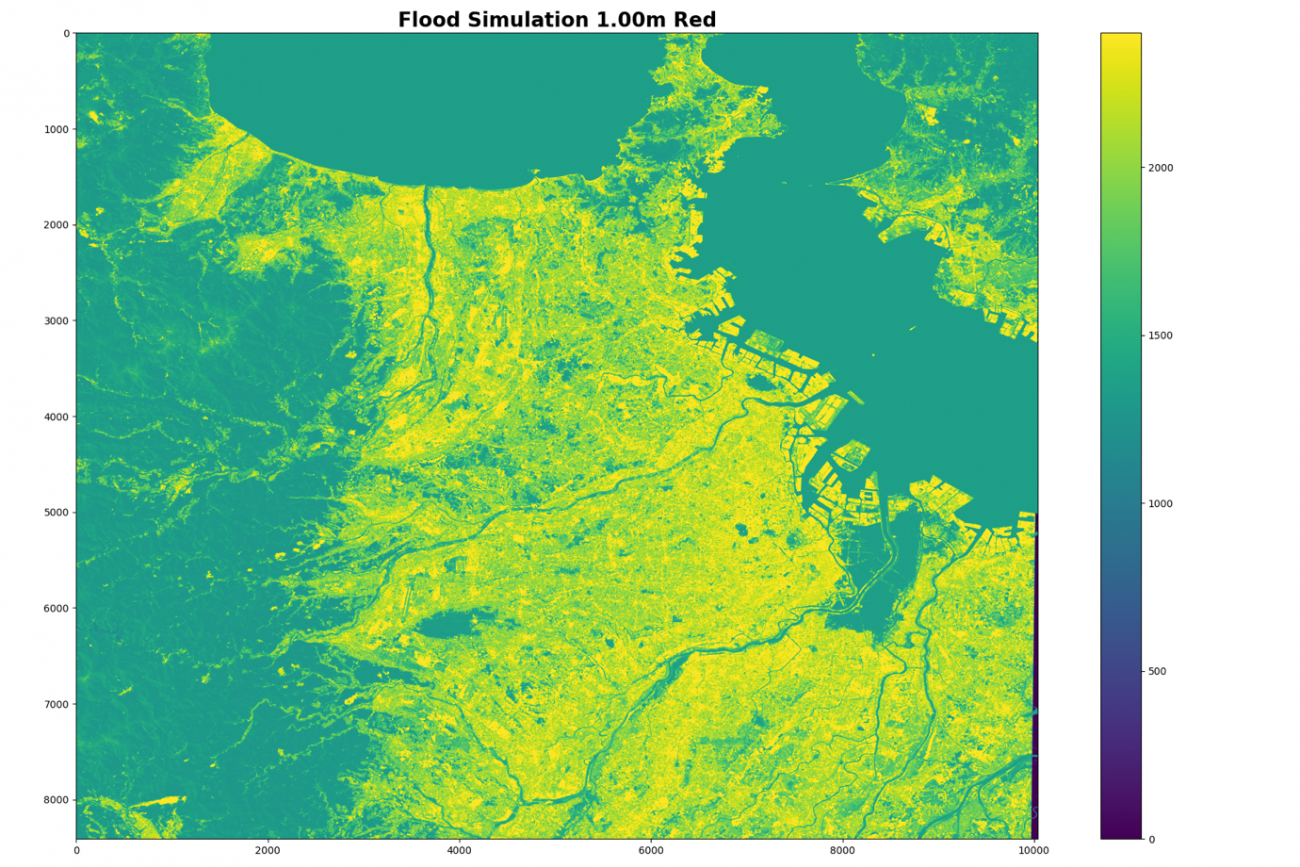
今回は海や河川の氾濫などで洪水被害の状況をシミュレーションして、教師データとして使えるような衛星データを作り出します。その後、そのデータを用いて予測モデルを作成するまでを紹介します。

また、本記事の特徴として、利用する衛星データは光学のデータです。近年はSAR衛星を用いた洪水のエリアや浸水深予測を行うケースが増えていますが、どのように光学衛星のデータを利用して浸水深の予測をするのかという点でも興味深い事例として紹介できればと考えています。

衛星データと標高モデル

使用する衛星は Sentinel-2 という光学衛星です。バンドは B2, B3, B4 の所謂可視光の画像です。以下の記事で光学衛星と光の特性について詳説しています。

データの取得については最近買収されて話題になった Sentinel Hub から取得しました。プラットフォームの役割や Sentinel Hub についてはこちらをご覧ください。

そして、もう一つ、地形情報として DEM (Digital Elevation Model)を使用します。すごく大雑把な説明としては標高情報になります。今回は国土地理院(https://fgd.gsi.go.jp/download/ref_dem.html)のDEMを使用します。メッシュは5m解像度です。これは Sentinel-2 の解像度 10m より良いものとなります。
DEM については以下の記事をご覧ください。

再現性のためにデータ以下にて公開しています
https://drive.google.com/drive/folders/12u8zH6-7kVcOcKi-oeaDw53AeSxOJUOg

対象エリアは東京とします。では、実際のデータを見ていきましょう。

Sentinel-2 バンド B2 (凡例: 赤)

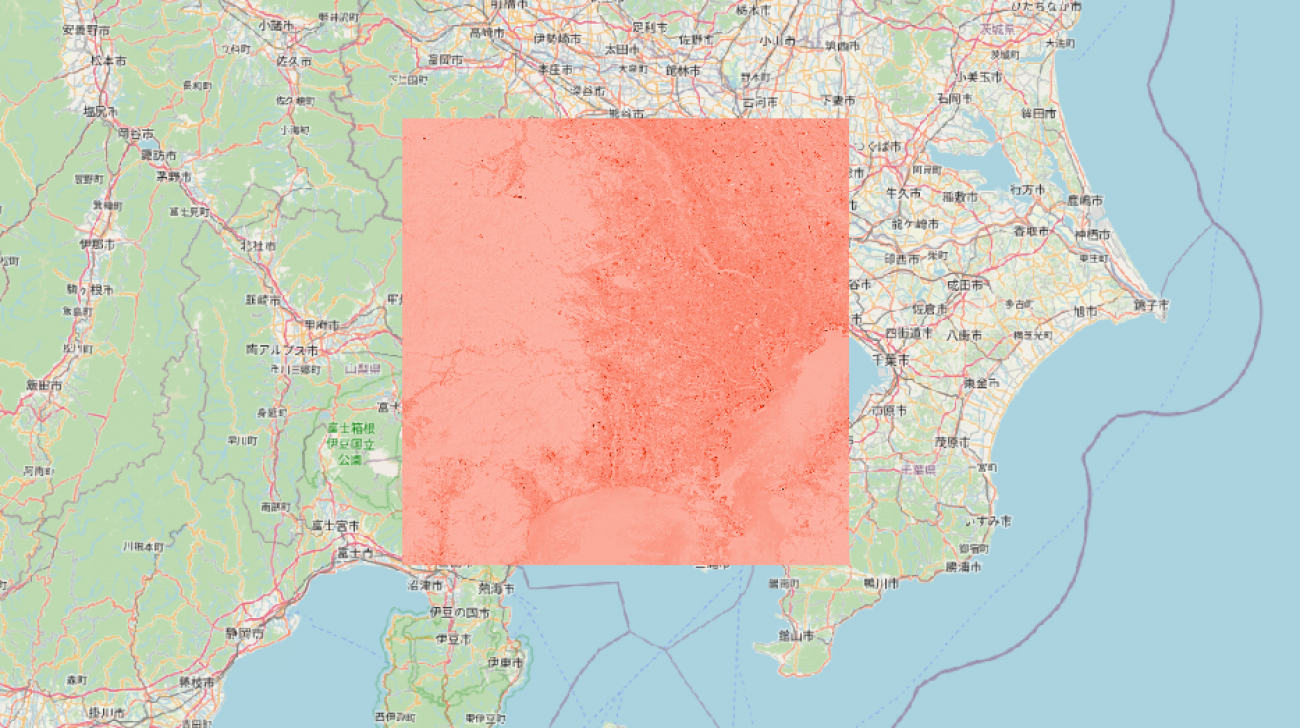
DEM (凡例: 青)

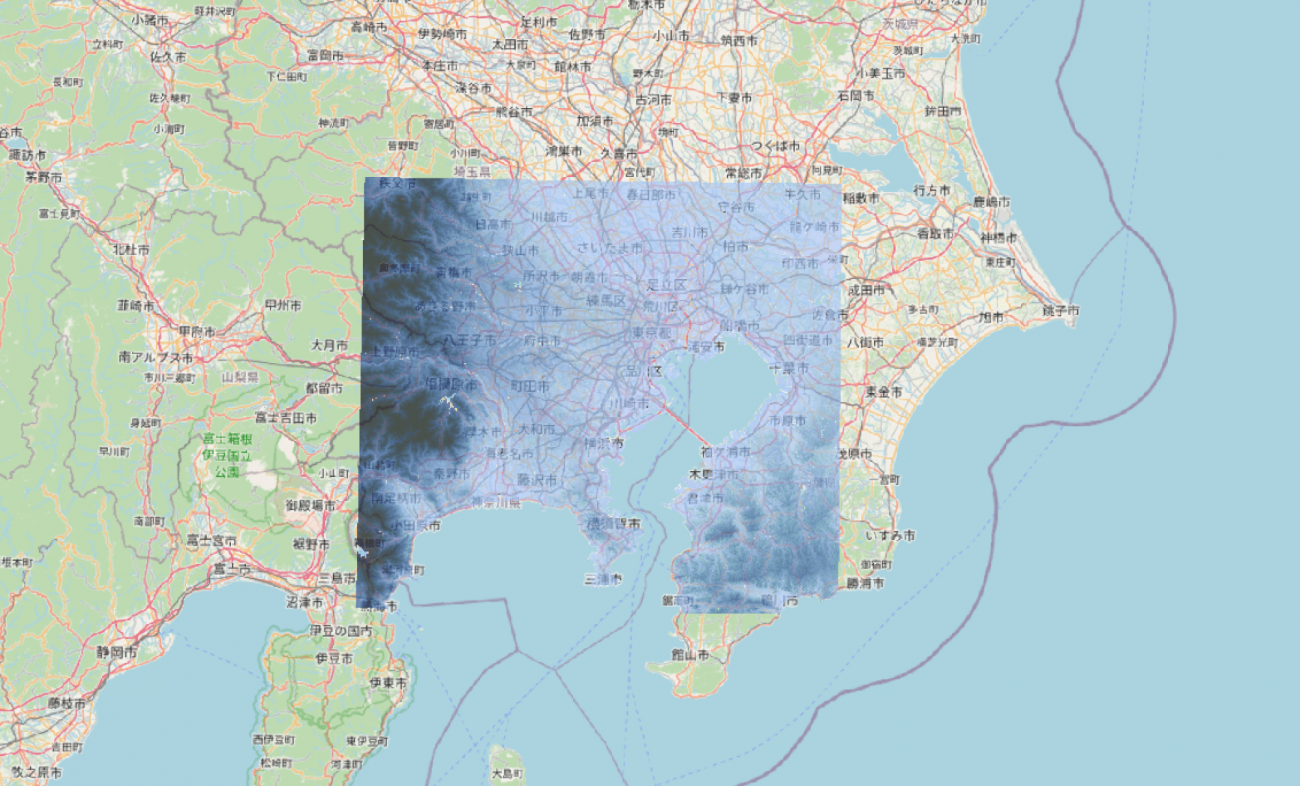
それぞれをレイヤーで重ねて表示します。

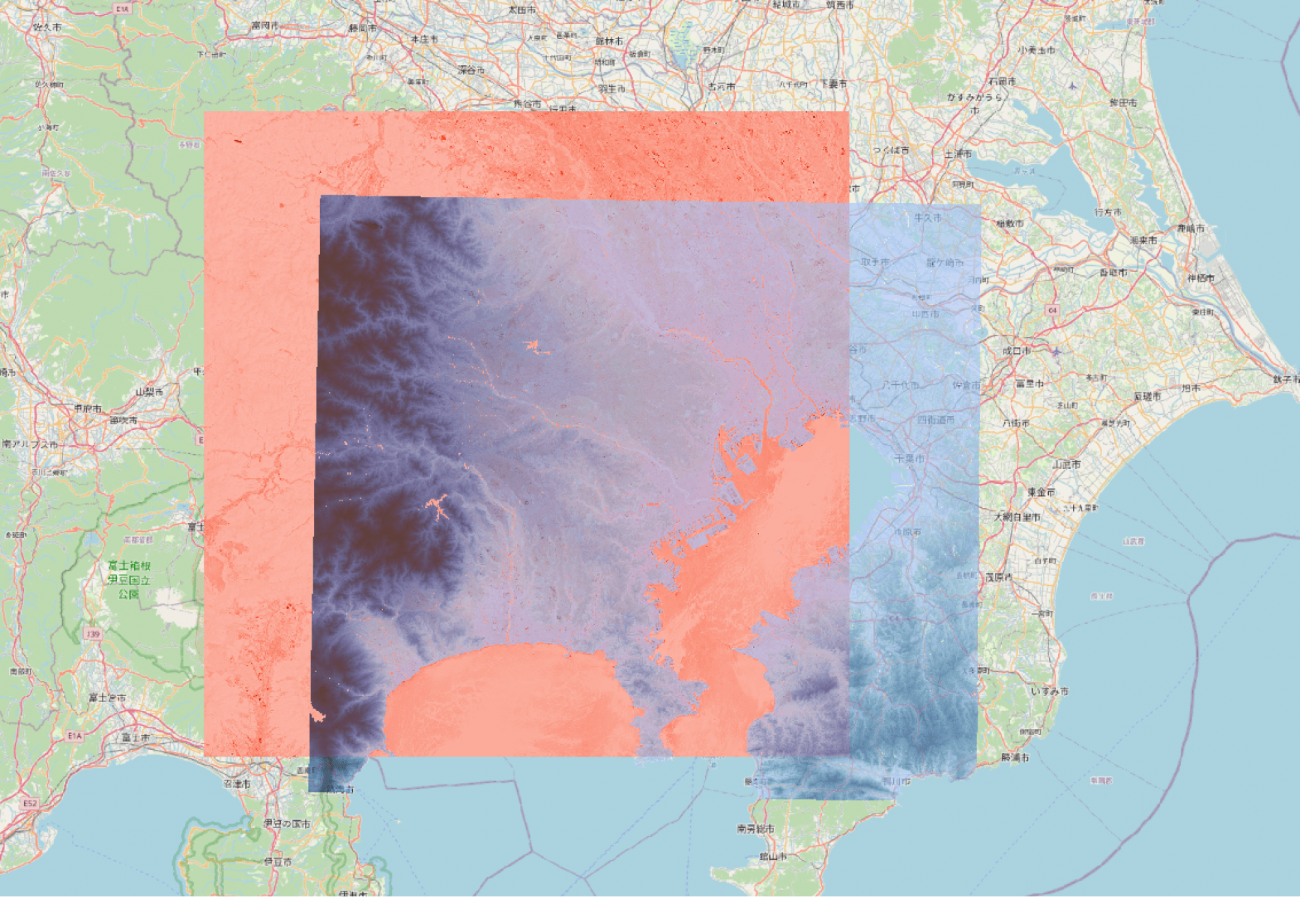
もっと東京に寄った画像も見てみましょう。

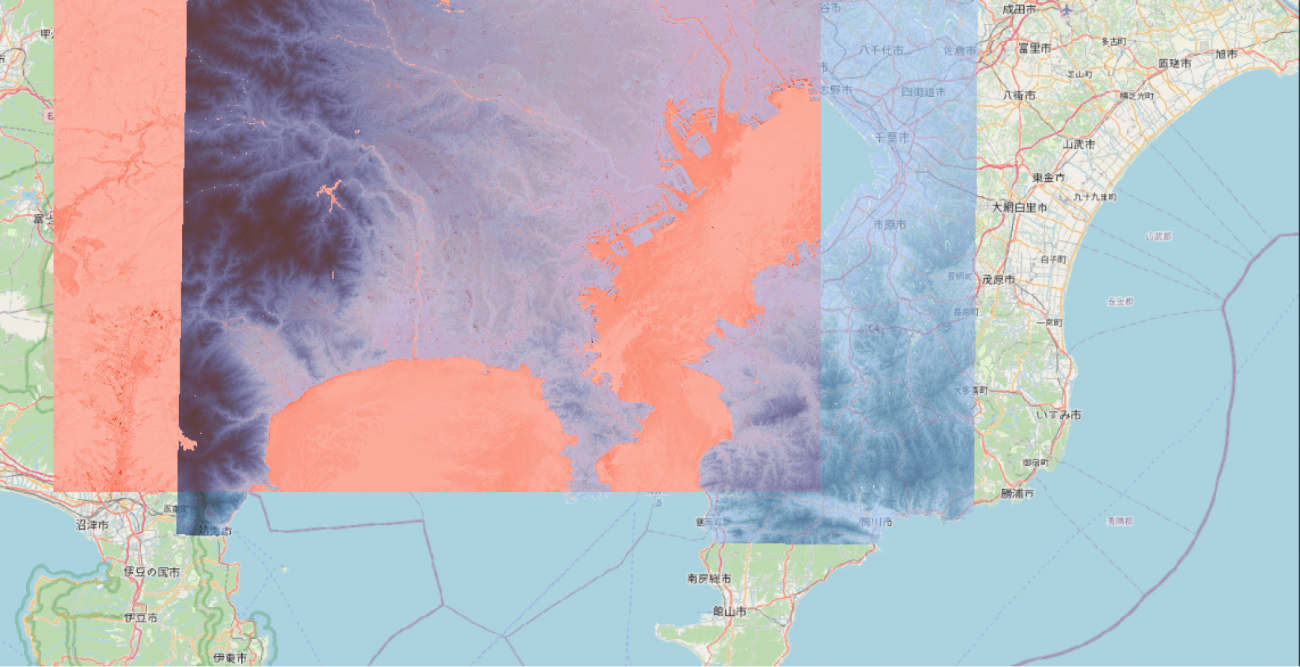
東京の埠頭が高くなっていることや、逆に川や池が低いことも見て取れますね。

次に、両方のデータが存在する場所でくり抜きます。左上の端点 (139.00331,35.99591) と右下の端点(140.00690,35.15523)で処理をします。
(CRS: `WGS84`)

DEM の地理空間処理

gdalwarp -te 139.00331 35.99591 140.00690 35.15523 -t_srs EPSG:4326 -te_srs EPSG:4326 dem.tif dem_cut.tif

可視光画像の地理空間処理

gdalwarp -te 139.00331 35.99591 140.00690 35.15523 -t_srs EPSG:4326 -te_srs EPSG:4326 R10m/B02.jp2 R10m/B02_cut.tif
gdalwarp -te 139.00331 35.99591 140.00690 35.15523 -t_srs EPSG:4326 -te_srs EPSG:4326 R10m/B03.jp2 R10m/B03_cut.tif
gdalwarp -te 139.00331 35.99591 140.00690 35.15523 -t_srs EPSG:4326 -te_srs EPSG:4326 R10m/B04.jp2 R10m/B04_cut.tif

くり抜く地理空間処理については以下に方法の説明や例がありますのでご覧ください。

くり抜いた画像を見て確認します。

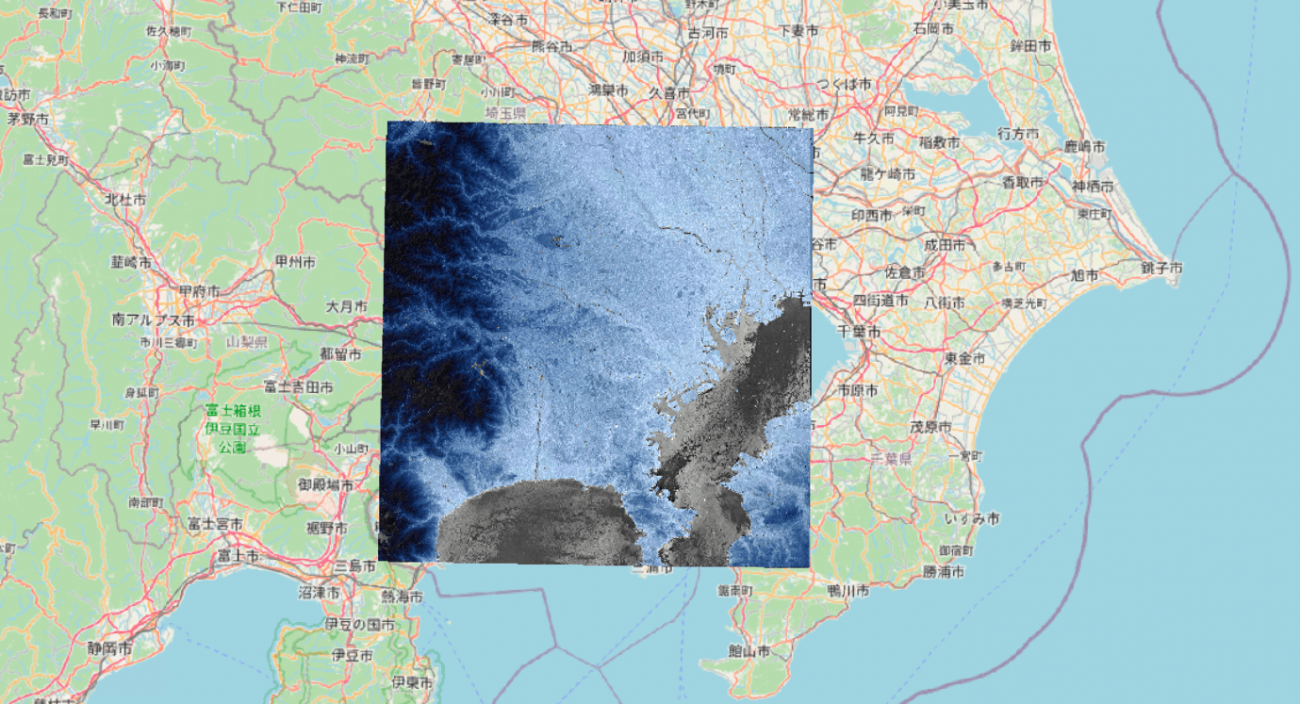
では、コードで処理していきましょう

PATH_B2  = '../sample/B02_cut.tif'
PATH_DEM = '../sample/dem_cut.tif'

Sentinel-2 の青バンドを読み込んで可視化します。

b2 = tifffile.imread(PATH_B2)
b2 = b2.astype(np.float32)

plt.imshow(b2, cmap='plasma', vmin=0., vmax=8000.)
plt.colorbar(shrink=0.75)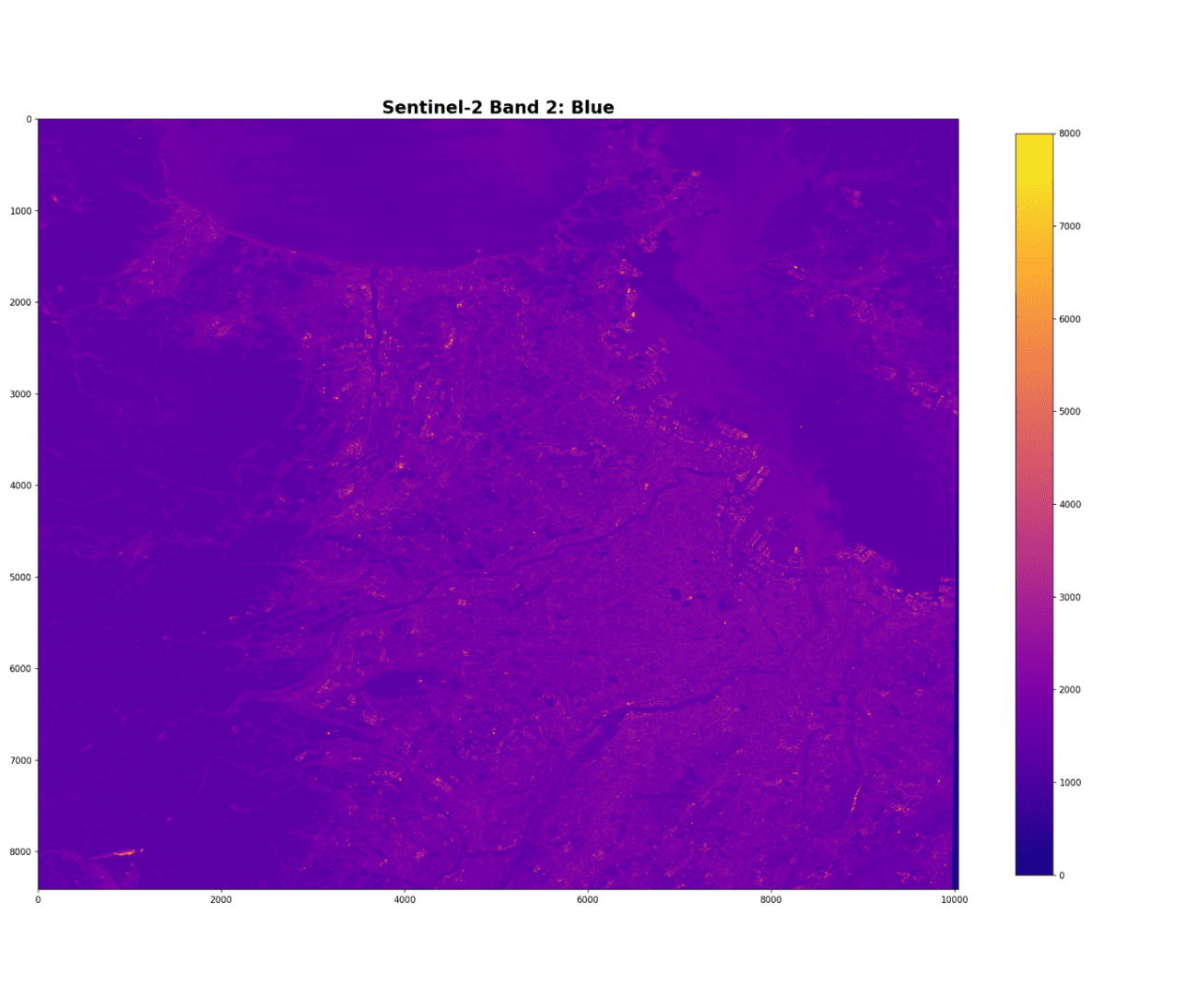

DEMのラスター画像を読み込んで可視化します。

dem = tifffile.imread(PATH_DEM)
dem[np.isnan(dem)] = -1
dem = dem.astype(np.float32)

plt.imshow(dem, cmap='terrain', vmin=0., vmax=50.)
plt.colorbar(shrink=0.75)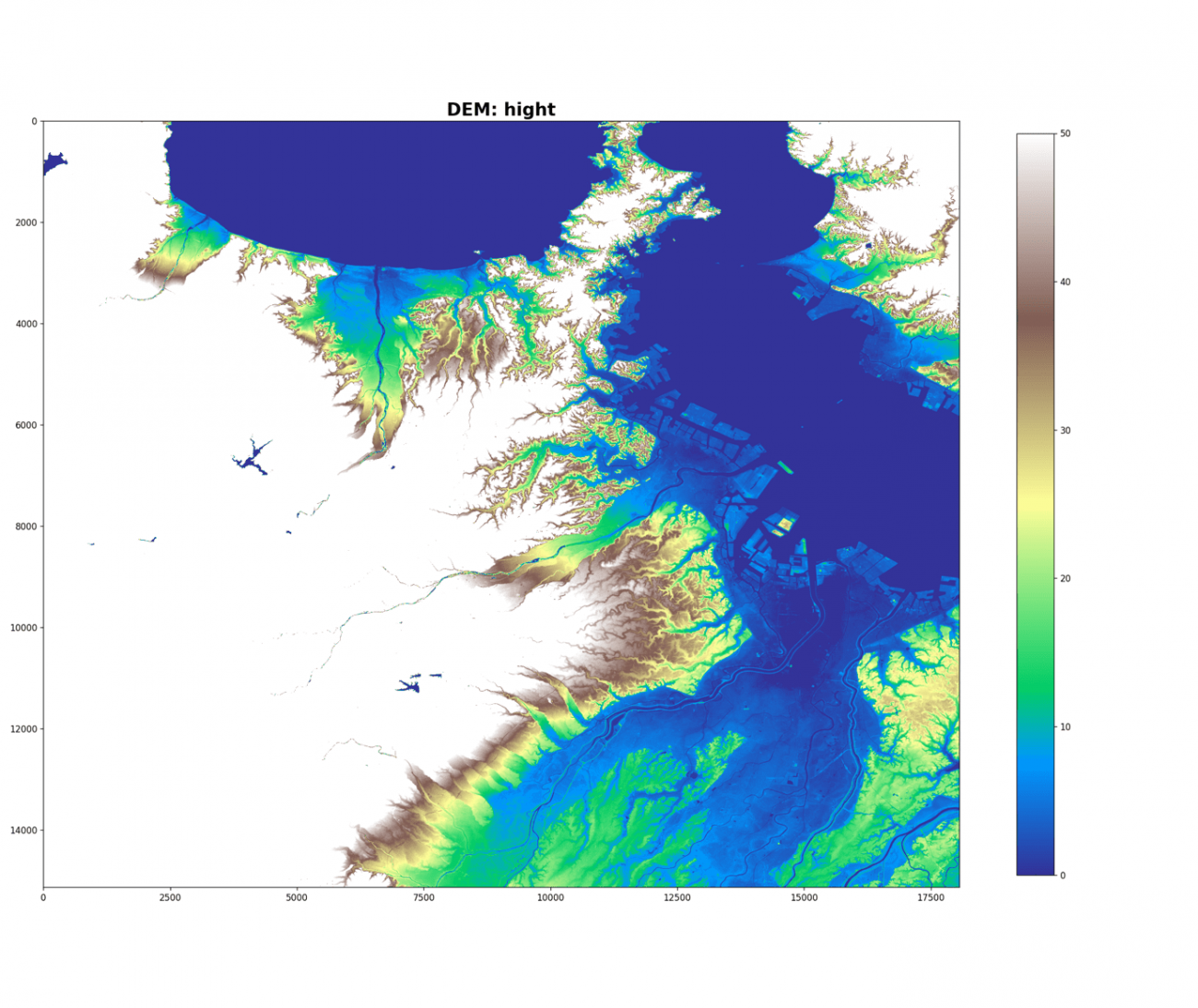

お気づきだと思いますが、衛星が昇交軌道から撮像していることと撮像方向の関係で上下左右が逆転しています。

ピクセル解像度を確認します。

b2.shape, dem.shape

出力結果：((8412, 10042), (15132, 18065))

今回は衛星データ自体をメインに扱いたいので DEM の解像度を下げて揃えます。

dem = cv2.resize(dem, (b2.shape[1], b2.shape[0]), interpolation=cv2.INTER_LINEAR)
dem.shape

出力結果：(8412, 10042)

洪水シミュレーション

洪水のシミュレーションでも何をシミュレーションするかは千差万別です。本記事では、仮想の海面を作成することで、浸水被害のでた衛星データをシミュレーションします。

それでは仮想海面を作成していきましょう。まずは、DEM情報から標高0メートルの場所、即ち海である領域のみのマスクを可視化します。

b2_sea = np.where(dem == -1, b2, 0)

plt.imshow(b2_sea, cmap='winter_r', vmin=0., vmax=3000.)
plt.colorbar(shrink=0.75,)
plt.show();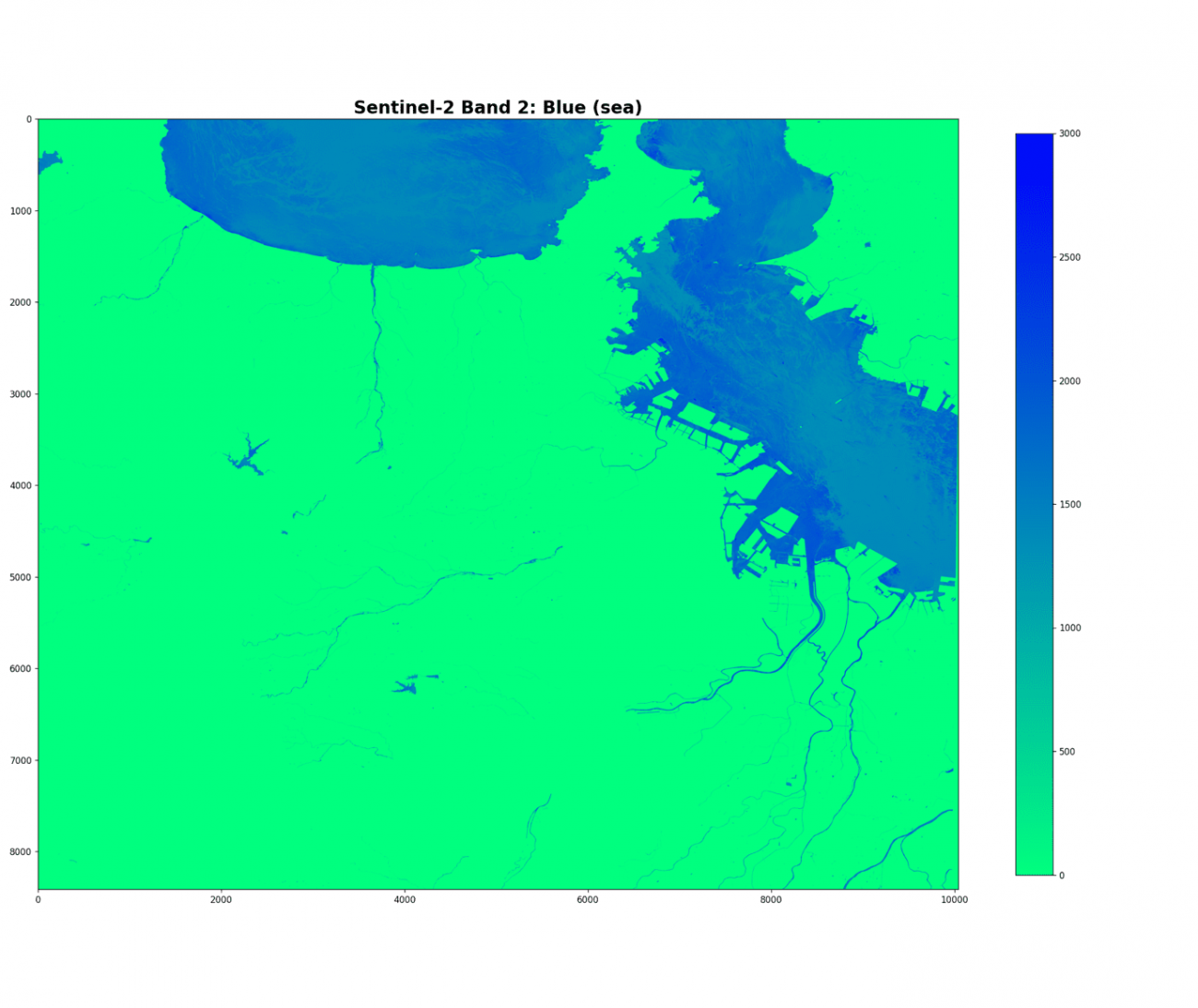

海面が見えてきたので標高0メートルのマスクされていない青波長の強度分布を見てみます。

plt.hist(b2_sea[b2_sea > 1].ravel(), bins=100, range=(1200., 2300.), fc='b', ec='k')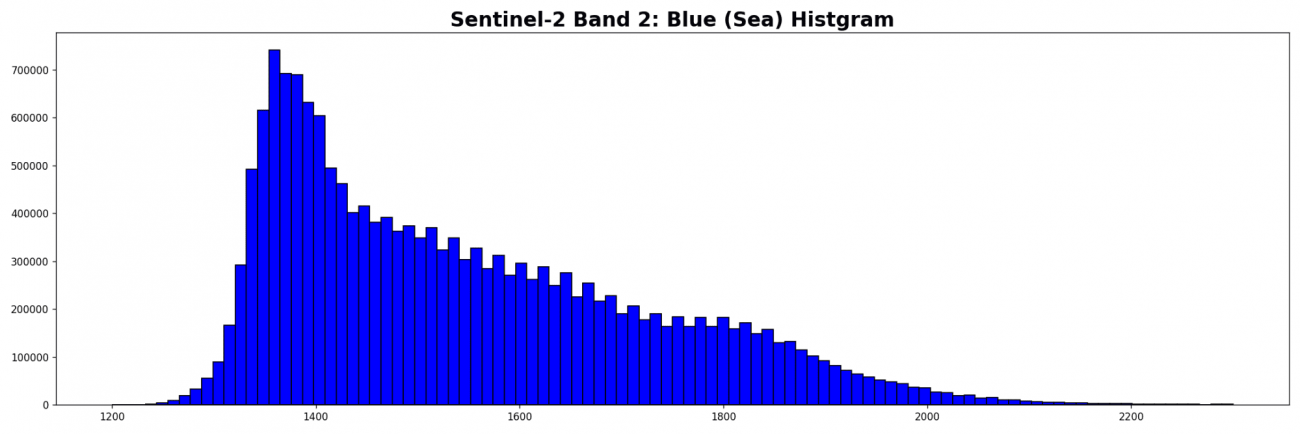

標高0メートルの場所だからすべてが海面であるわけではありません。上記の画像には船舶や波などが含まれています。ここでは海面以外の物体は白く反射すると仮定して値が大きくなっているとします。そのように考えると、分布の右裾は海面以外の物体であると推測できます。

海面だけの場合は波浪が規則性がなく、光が反射する方向がランダムだと仮定すれば、海面の反射強度は正規分布になります。反射強度の値が低く、分布解析をした衛星データから海面の割合が多いと判断し、左端の山が海面のみ分布だと推察できます。よって左端の山に対して正規分布を作成します。

gauss_sea = np.random.normal(loc=1375, scale=50 , size=(len(b2_sea[b2_sea > 1])))

plt.hist(gauss_sea.ravel(), bins=100, range=(1200., 2300.), fc='r', ec='k')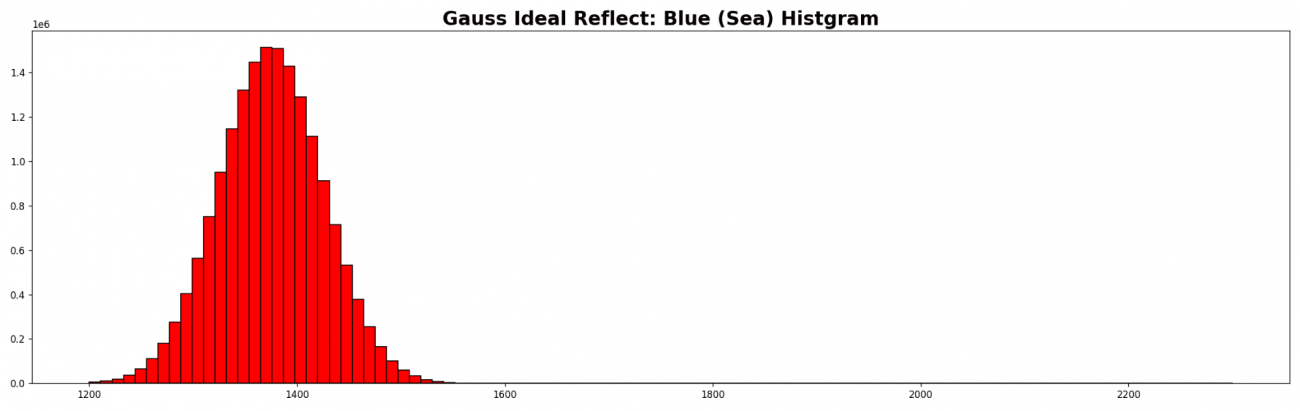

分布を重ねてみましょう。

plt.hist(b2_sea[b2_sea > 1].ravel(), bins=100, range=(1200., 2300.), fc='b', ec='k', alpha=0.6)
plt.hist(gauss_sea.ravel(), bins=100, range=(1200., 2300.), fc='r', ec='k', alpha=0.6)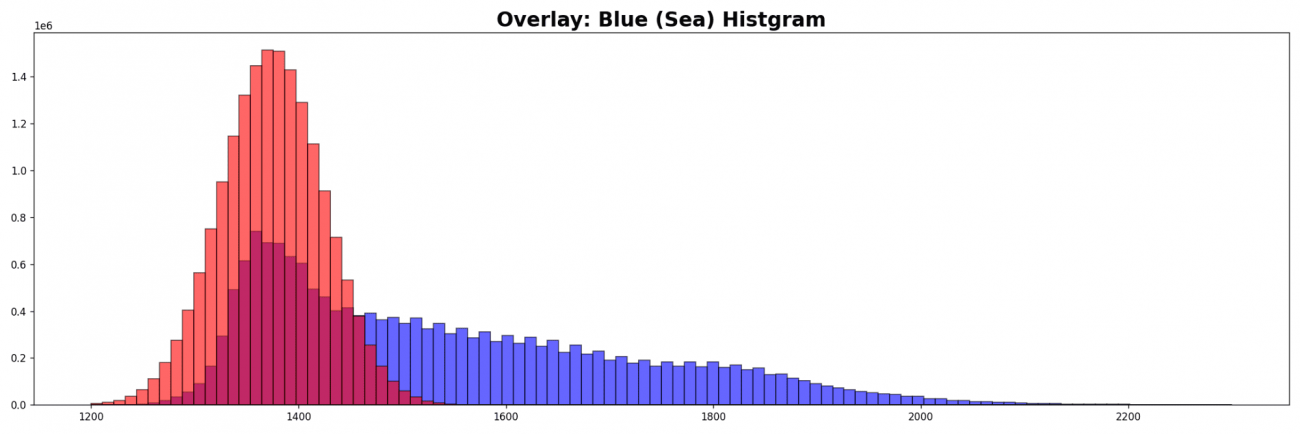

理想反射だと最小は 1100、最大は 1600 くらいなので 1600 を目安にします。より正確なデータを求める場合は船舶のポリゴンの値を調査するなども行います。

b2_sea_points = b2_sea[b2_sea > 1]
b2_sea_points = b2_sea_points[b2_sea_points < 1600]

plt.hist(b2_sea_points, bins=100, range=(1200., 2300.), fc='b', ec='k')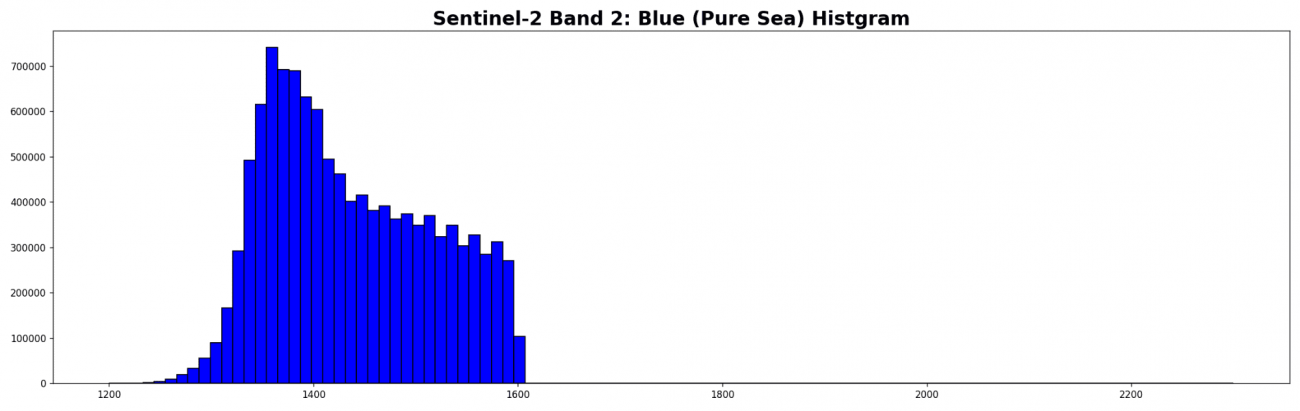

できたこの分布が理想の純粋な海面値になります。さっそく、この値から衛星画像のサイズの仮想海面を作成しましょう。

virtual_sea = random.choices(b2_sea_points, k=math.prod(b2.shape))
virtual_sea = np.array(virtual_sea).reshape(b2.shape)

plt.imshow(virtual_sea, cmap='Blues', vmin=1200., vmax=1650.)
plt.colorbar(shrink=0.75)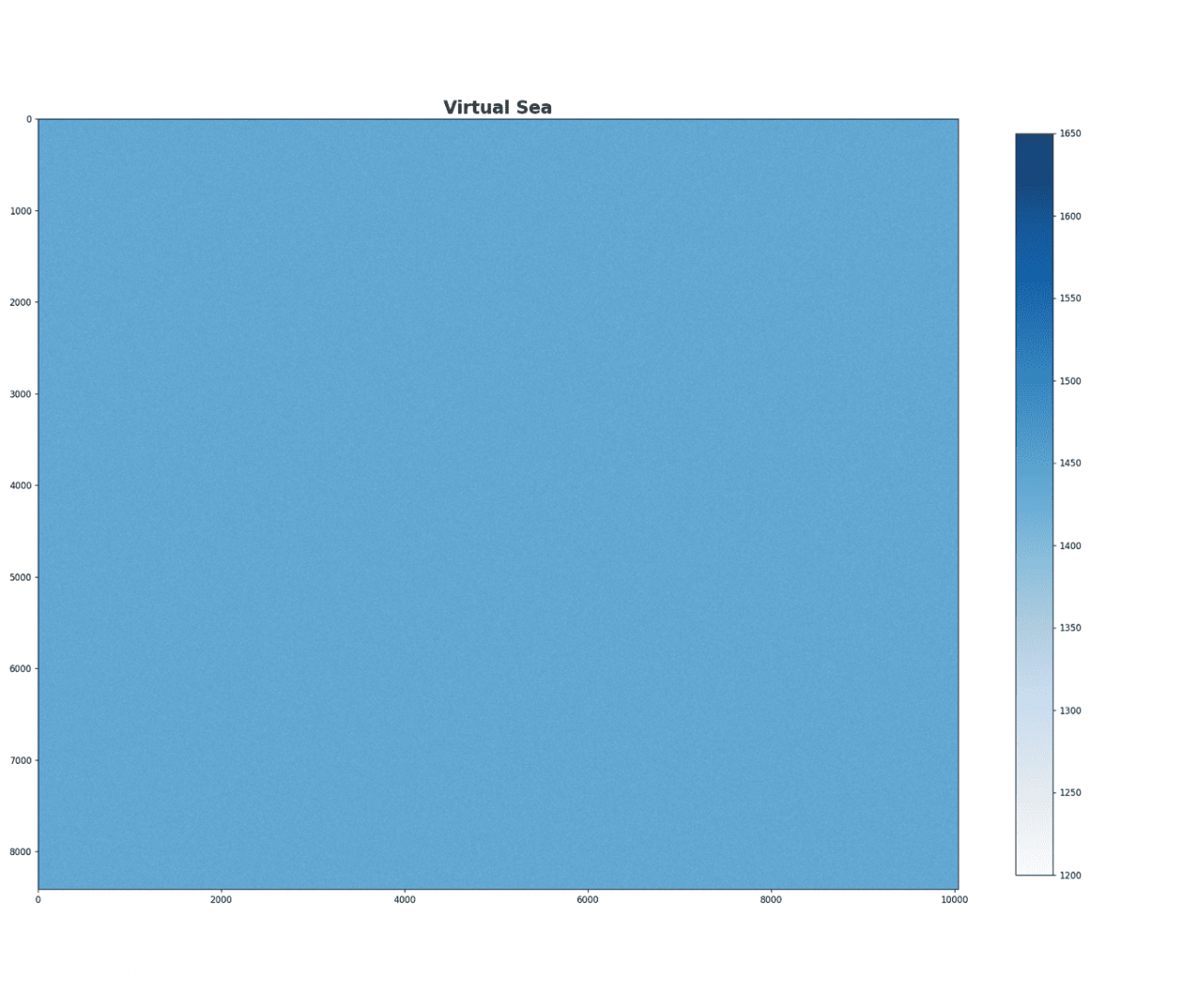

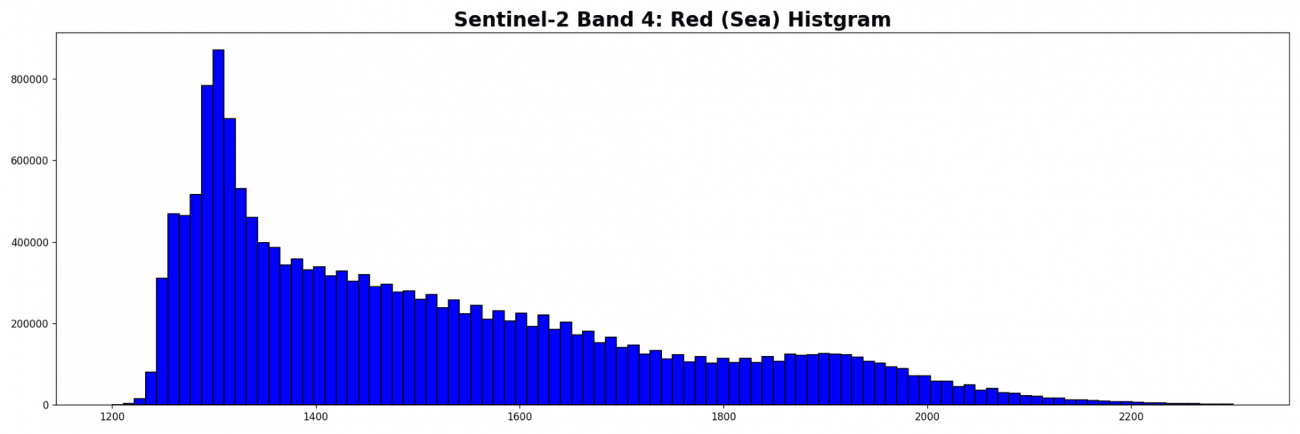
同様の処理を B3(緑), B4(赤) についても行います。

PATH_B3  = '../sample/B03_cut.tif'
b3 = tifffile.imread(PATH_B3)
b3 = b3.astype(np.float32)
b3_sea = np.where(dem == -1, b3, 0)

plt.hist(b2_sea[b2_sea > 1].ravel(), bins=100, range=(1200., 2300.), fc='b', ec='k')

PATH_B4  = '../sample/B04_cut.tif'
b4 = tifffile.imread(PATH_B4)
b4 = b4.astype(np.float32)

b4_sea = np.where(dem == -1, b4, 0)
plt.hist(b4_sea[b4_sea > 1].ravel(), bins=100, range=(1200., 2300.), fc='b', ec='k')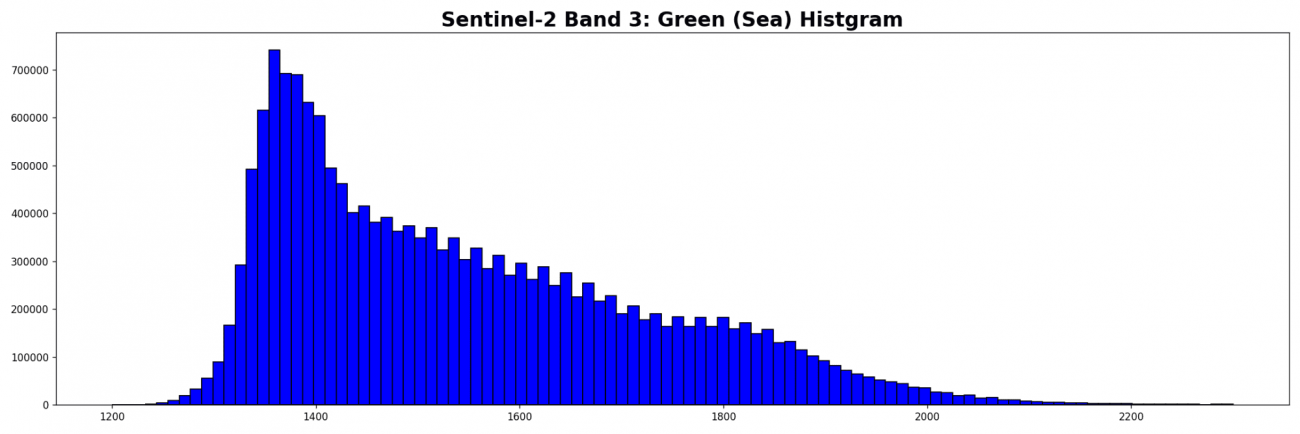

b3_sea_points = b3_sea[b3_sea > 1]
b3_sea_points = b3_sea_points[b3_sea_points  1]
b4_sea_points = b4_sea_points[b4_sea_points < 1500]

今度はDEMの分布も見てみます。

plt.hist(dem[dem > 0].ravel(), bins=100, range=(0., 50.), fc='y', ec='k')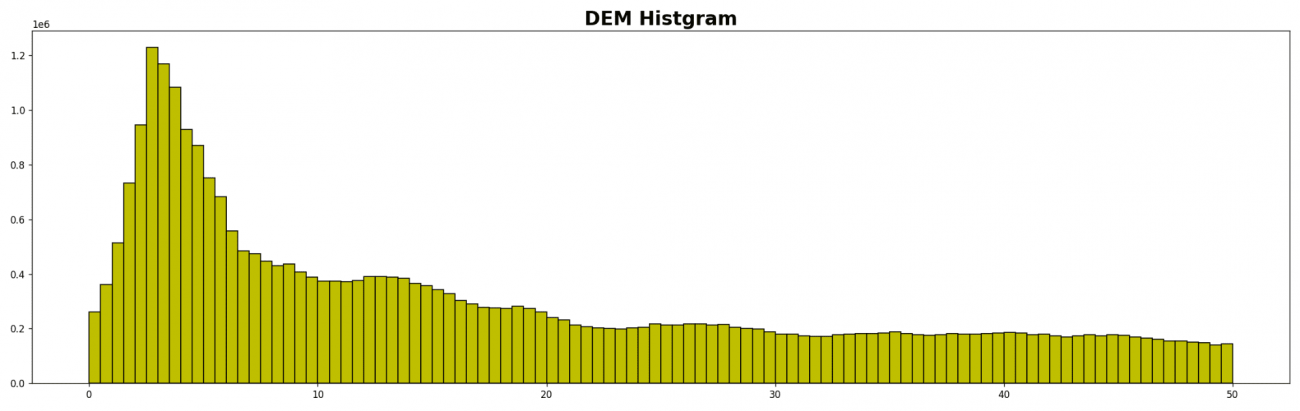

2〜5メートルが一番多く、それ以上の高さとなると減りながら漸近しています。

step = 1
depthes = np.arange(0., 40., step=step)

特に理由はないですが、1メートル幅で標高0メートルから40メートル手前まで海面を上昇させていきます。

for i, depth in tqdm(enumerate(depthes)):
    
    flood_bands = []
    
    for b_sea_points, _b in tqdm(zip([b2_sea_points, b3_sea_points, b4_sea_points], [b2, b3, b4])):
    
        # ramdom virtual sea
        virtual_sea = random.choices(b_sea_points, k=math.prod(_b.shape))
        virtual_sea = np.array(virtual_sea).reshape(_b.shape)
        
        # select flood area from dem
        flood = np.where(dem > depth, _b, virtual_sea)
        flood = flood.astype(np.float32)
        flood_bands.append(flood)
        
    # merge bands
    flood = np.stack(flood_bands, axis=2)
    tifffile.imsave(os.path.join(PATH_DATA, f'flood_{depth:.2f}.tif'), flood)

シミュレーションした画像は保存して次の機械学習モデルの学習データにします。

では、経過を可視化します

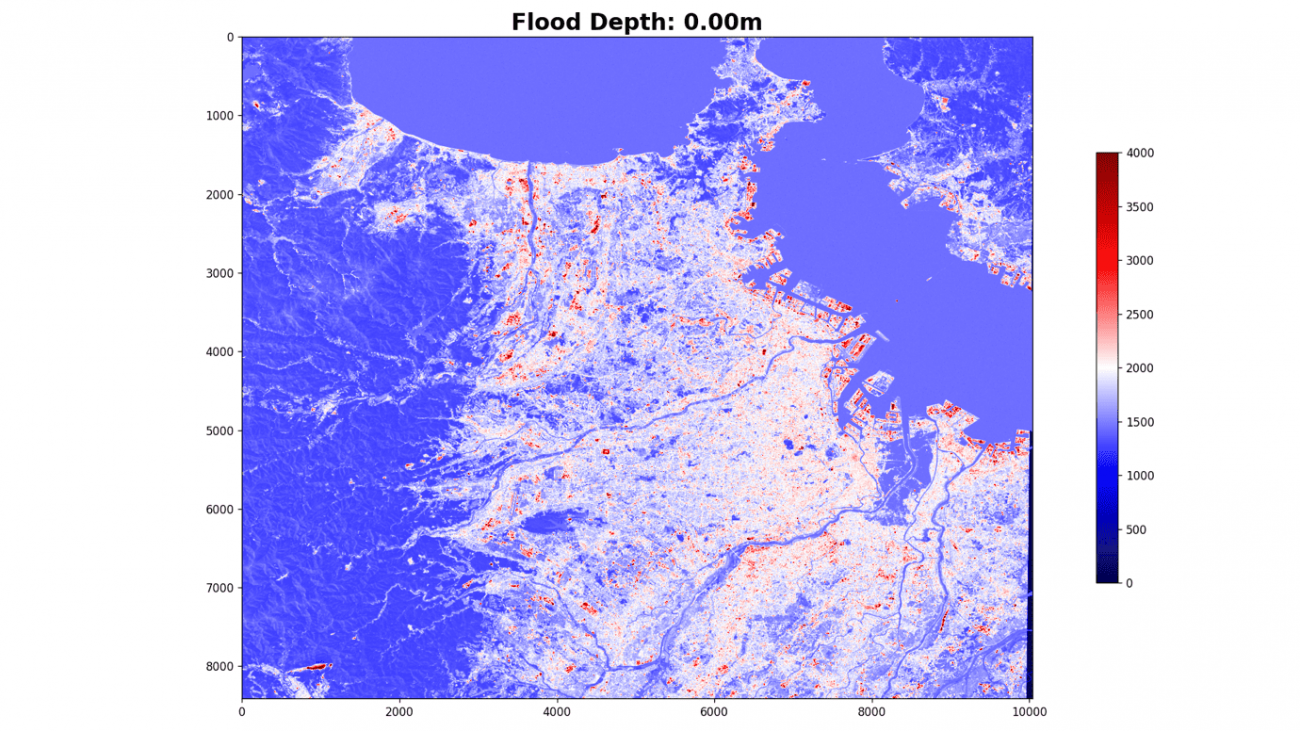
plt.imshow(flood[:, :, 0], cmap='seismic', vmin=0., vmax=4000.)
plt.colorbar(shrink=0.65)

海抜０メートル

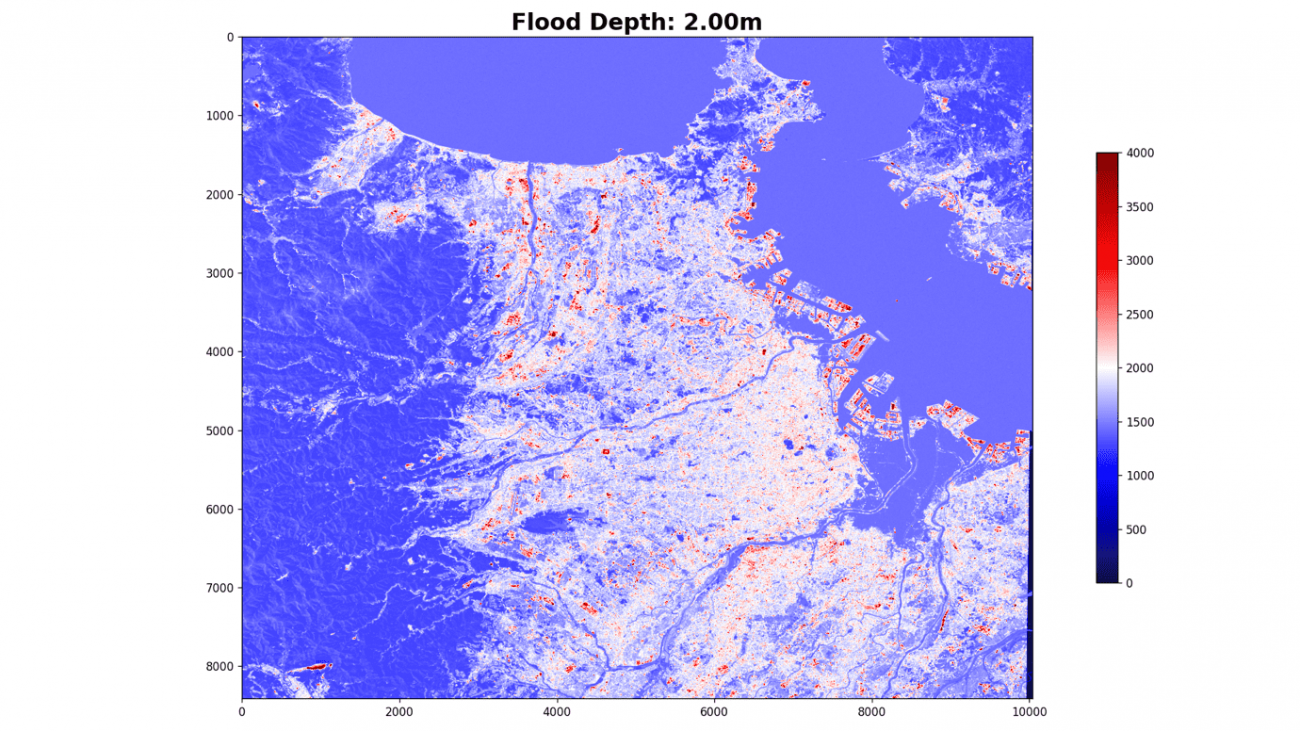
海抜２メートル

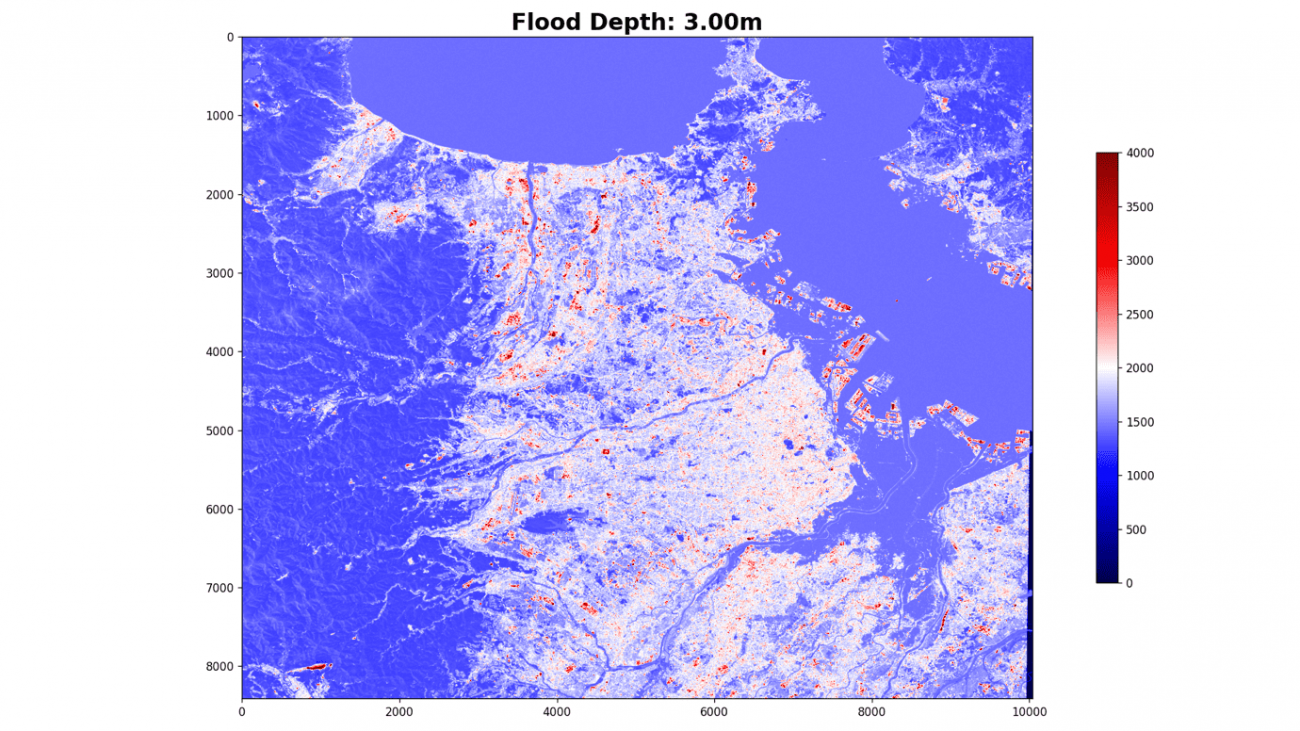
海抜３メートル

海抜５メートル

海抜１０メートル

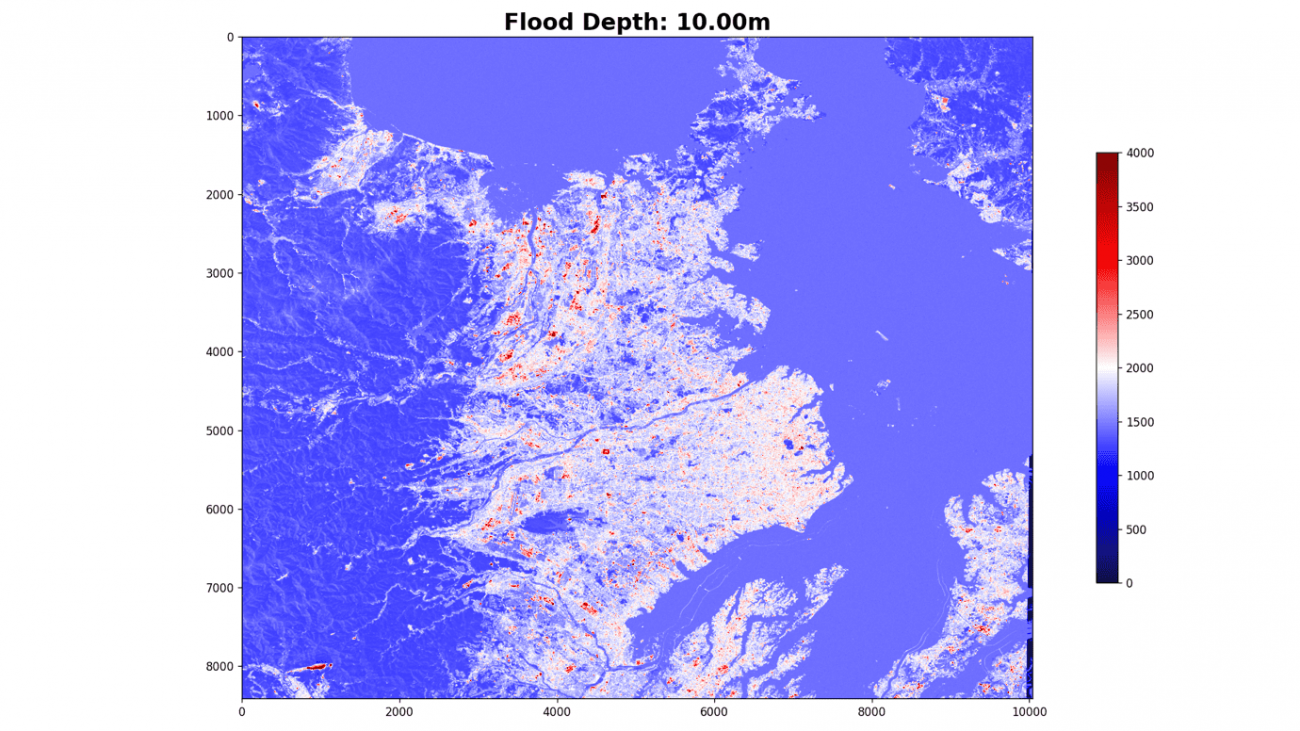
海抜１５メートル

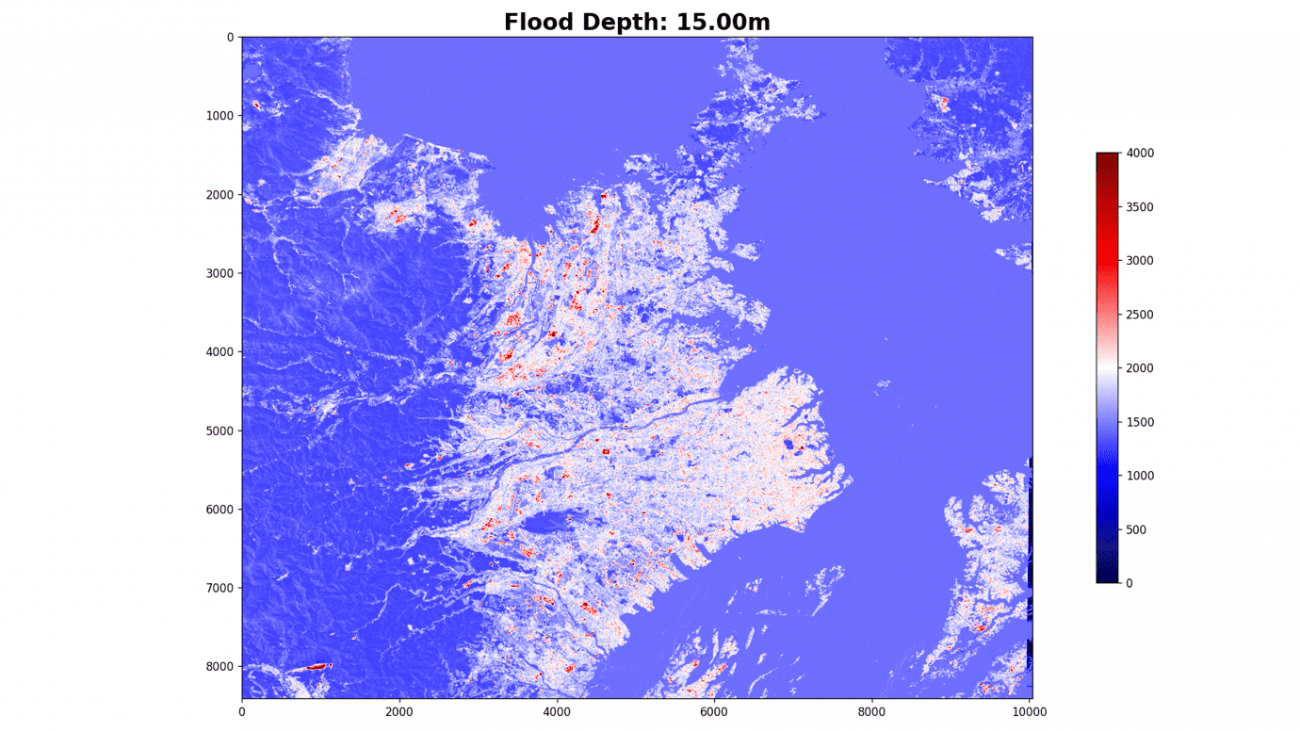
海抜２０メートル

海抜２５メートル

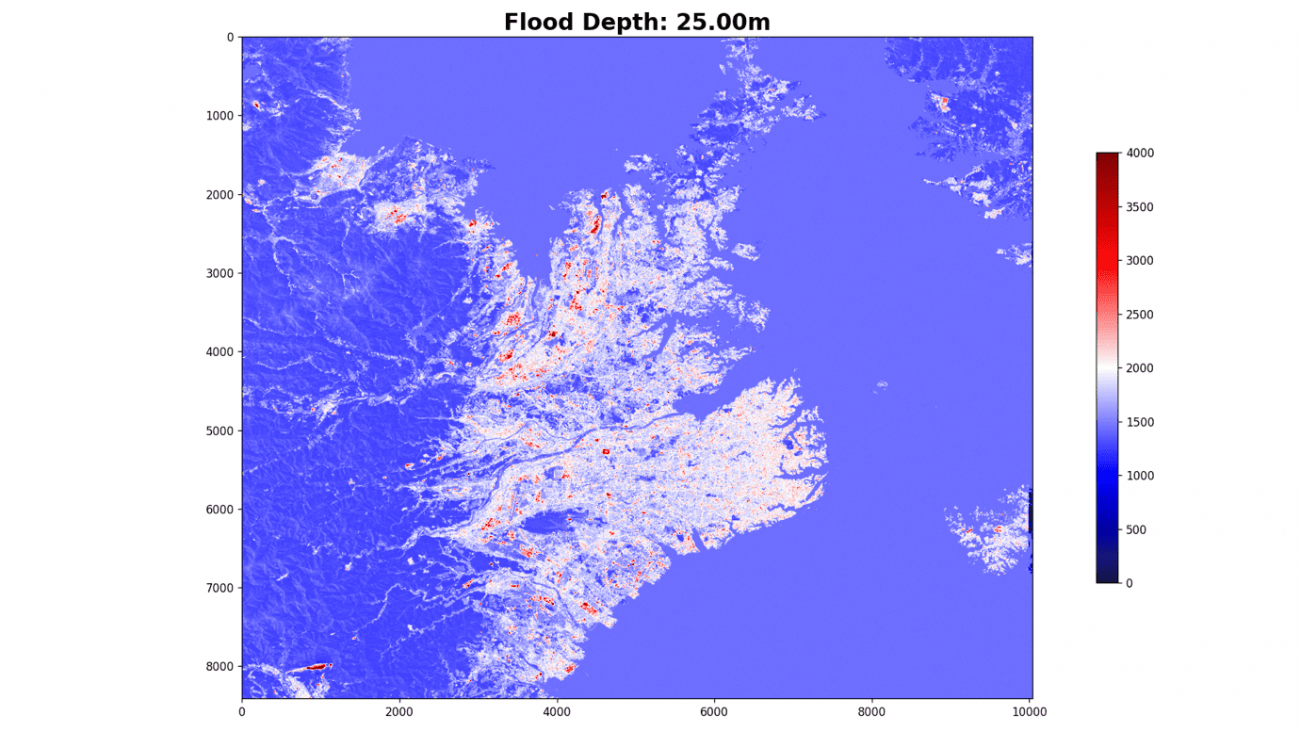
海抜３０メートル

海抜３５メートル

浸水エリアの予測

仮想海面の衛星データができたのでこの仮想海面を予測することができれば、浸水域を検知するモデルが作成できます。

本記事では、機械学習の中でもディープラーニングを用いて検出していきます。まずは、学習するデータを可視化します。

flood_depth = 11.0

１１メートルについてみていきましょう。

PATH = f'../output/virtual_flood/flood_{flood_depth:.2f}.tif'
img = tifffile.imread(PATH).astype(np.float32)

plt.imshow(img[: ,:, 0], vmax=3000)
plt.colorbar()
plt.imshow(img[: ,:, 1], vmax=2800)
plt.colorbar()
plt.imshow(img[: ,:, 2], vmax=2400)
plt.colorbar()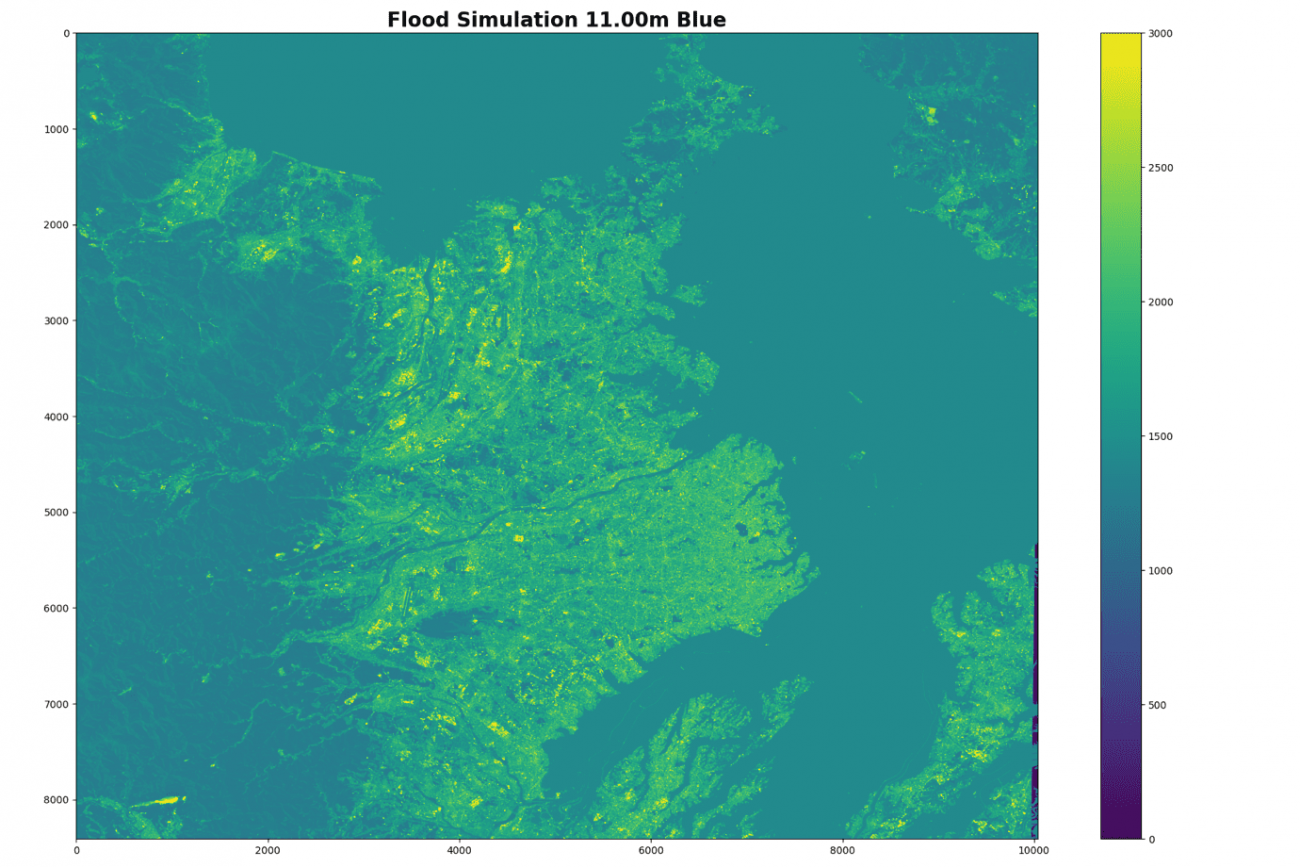

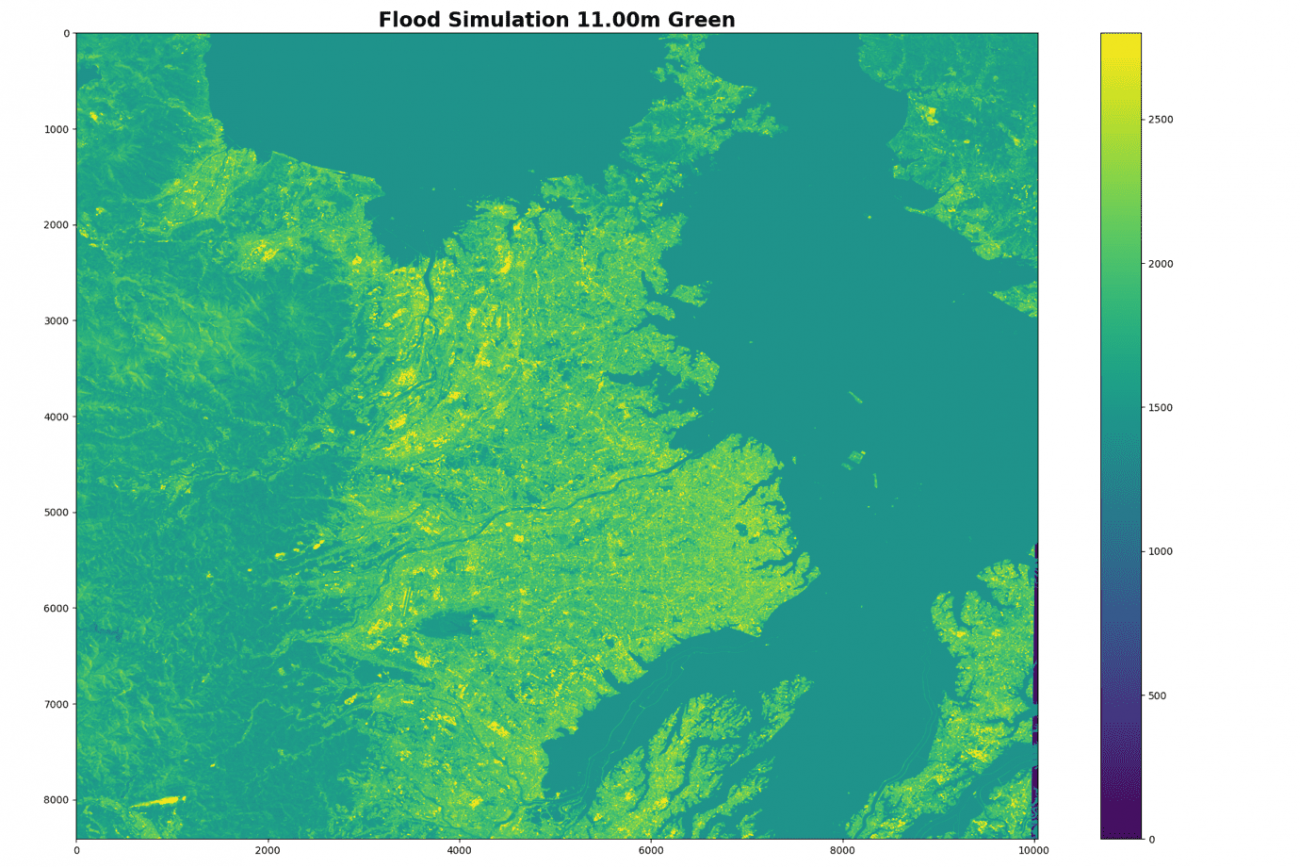
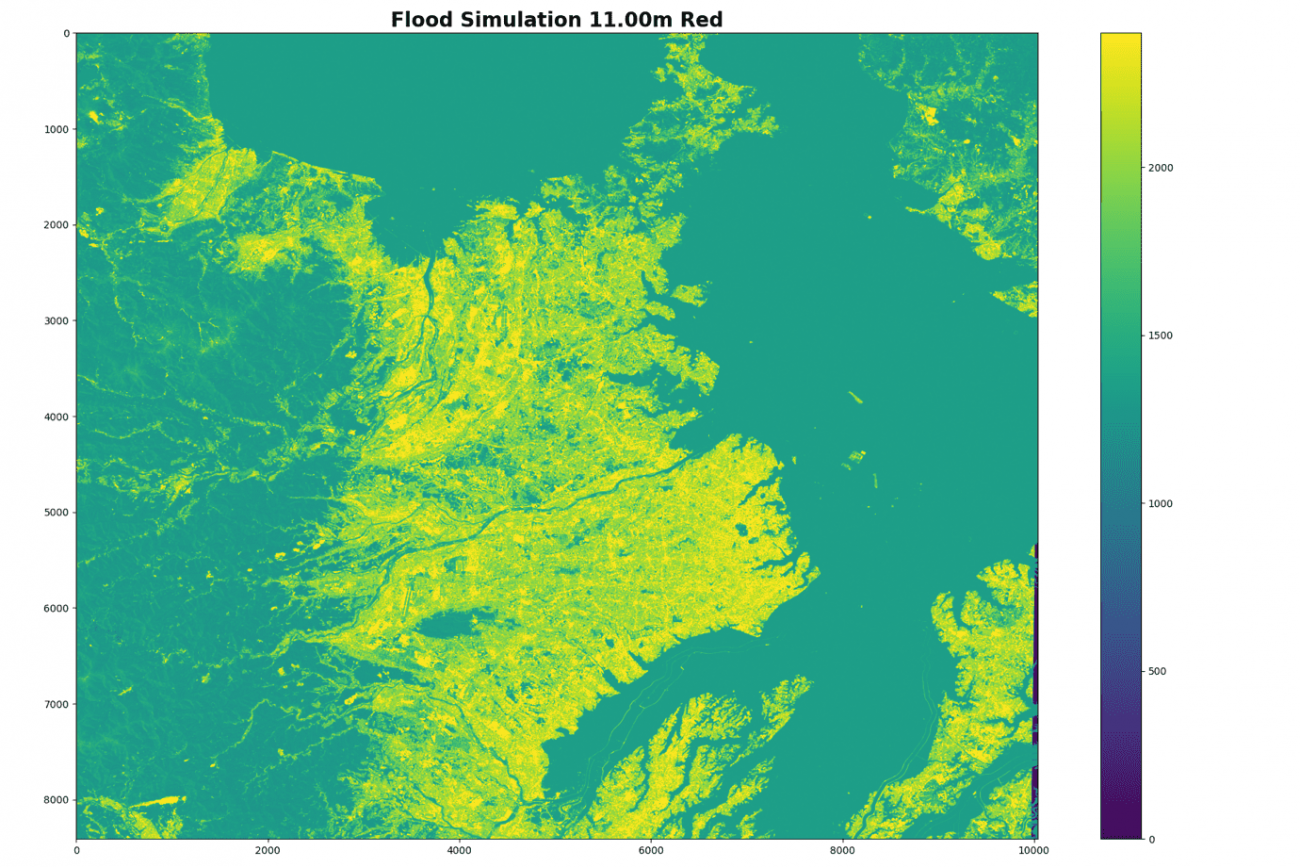
教師データの元となるDEMを可視化します。

PATH = f'../output/dem_resize_gt.tif'
gt = tifffile.imread(PATH).astype(np.float32)

plt.figure(figsize=(18, 12))
plt.title('DEM upto 200m', fontsize=20, fontweight='bold')
plt.imshow(gt, vmax=200)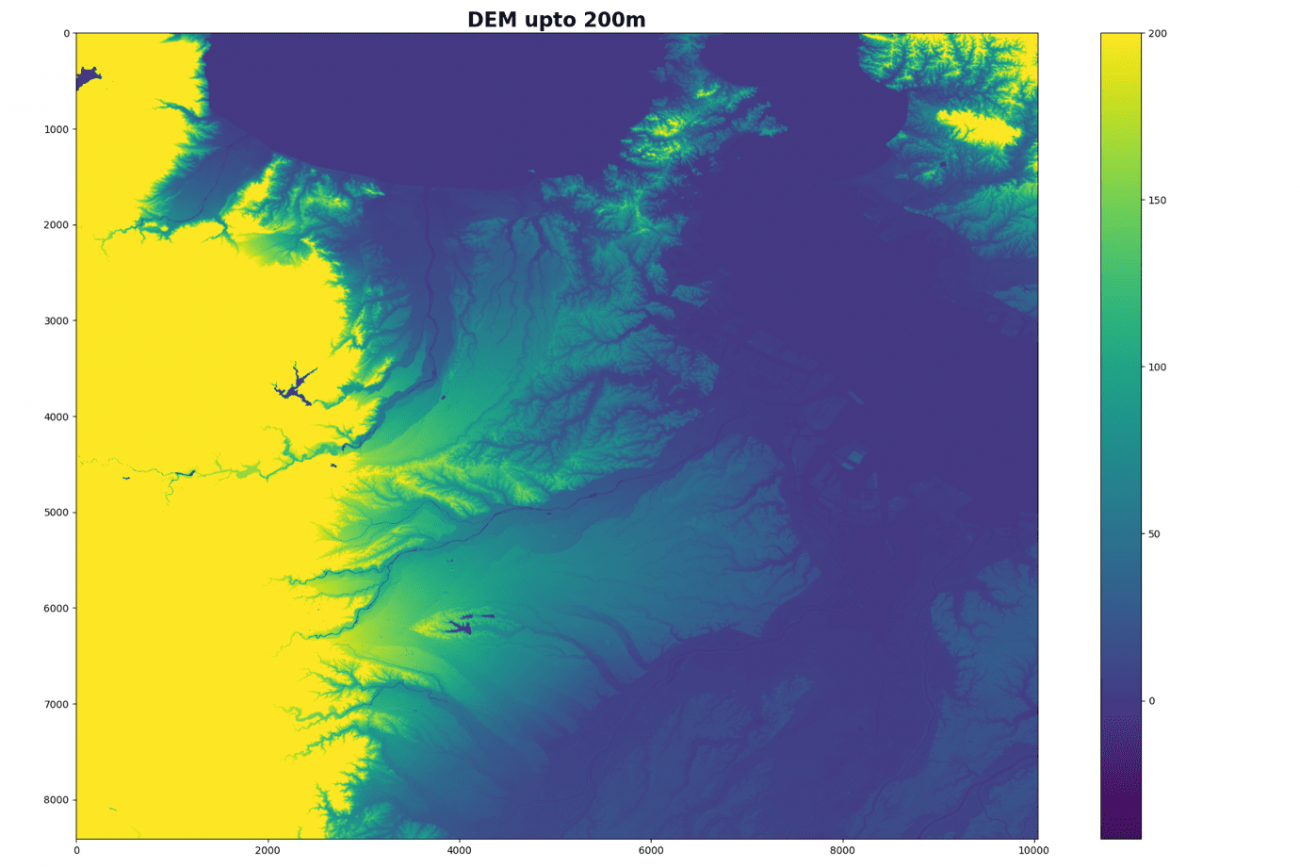

標高１１メートルの教師データを可視化します。

plt.imshow((gt > flood_depth).astype(np.float32), cmap='Reds')
plt.colorbar()

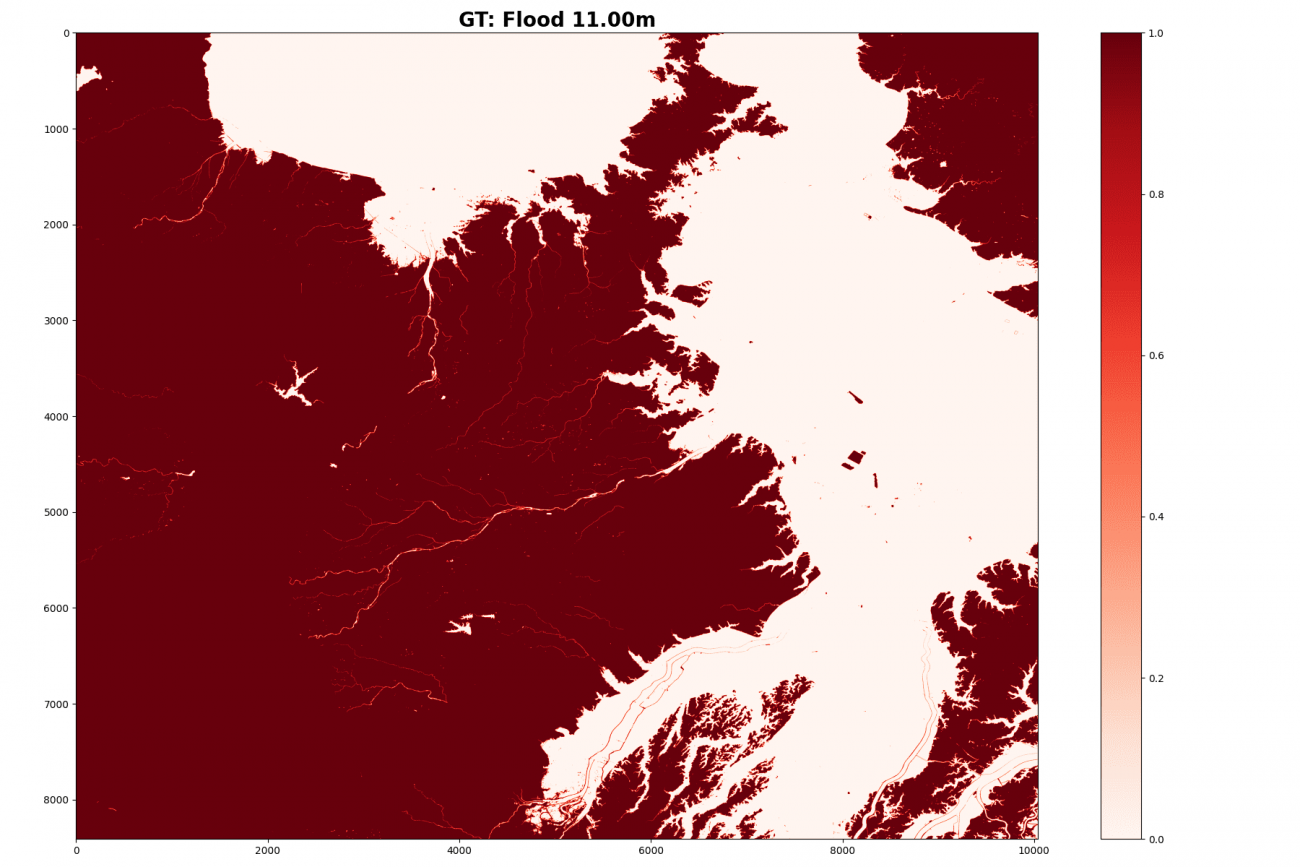
大きい画像のまま学習したいところですが、全部を同時に学習させるには、マシンスペックの物理的な限界があります。そこで細かいパッチに分割して学習していきます。ディープラーニングはSGD(確率的勾配降下法)というランダムにサンプリングすることで汎用解に辿り着く方法がベースとなっているため、パッチ処理する衛星画像とも相性が良いとされています。

シミュレーションした標高０メートルから４０メートルまでのデータ全てを処理します。

step = 1
depthes = np.arange(0., 40., step=step)

では、パッチのサイズを２５６四方で切っていきます。

IMG_SIZE = 256


patch_depths, patch_hs, patch_ws, patch_paths = [], [], [], []


for depth in tqdm(depthes):
    PATH = f'../output/virtual_flood/flood_{flood_depth:.2f}.tif'
    img = tifffile.imread(PATH).astype(np.float32)


    features = [img[:, :, 0], img[:, :, 1], img[:, :, 2], (gt < depth).astype(np.float32)]
    imgs = np.stack(features, axis=2) # Hight, Width, Channel:2


    for h in range(img.shape[0] // IMG_SIZE):
        for w in range(img.shape[1]  // IMG_SIZE):
          patch = imgs[h*IMG_SIZE:(h+1)*IMG_SIZE, w*IMG_SIZE:(w+1)*IMG_SIZE]


          PATH_PATCH = f'../output/modeling/z_depth{depth:.2f}_patch_h{str(h).zfill(3)}_w{str(w).zfill(3)}.npy'
          np.save(PATH_PATCH, patch)
          
          patch_depths.append(depth)
          patch_hs.append(h)
          patch_ws.append(w)
          patch_paths.append(PATH_PATCH)

確認のために、パッチ画像を可視化します。

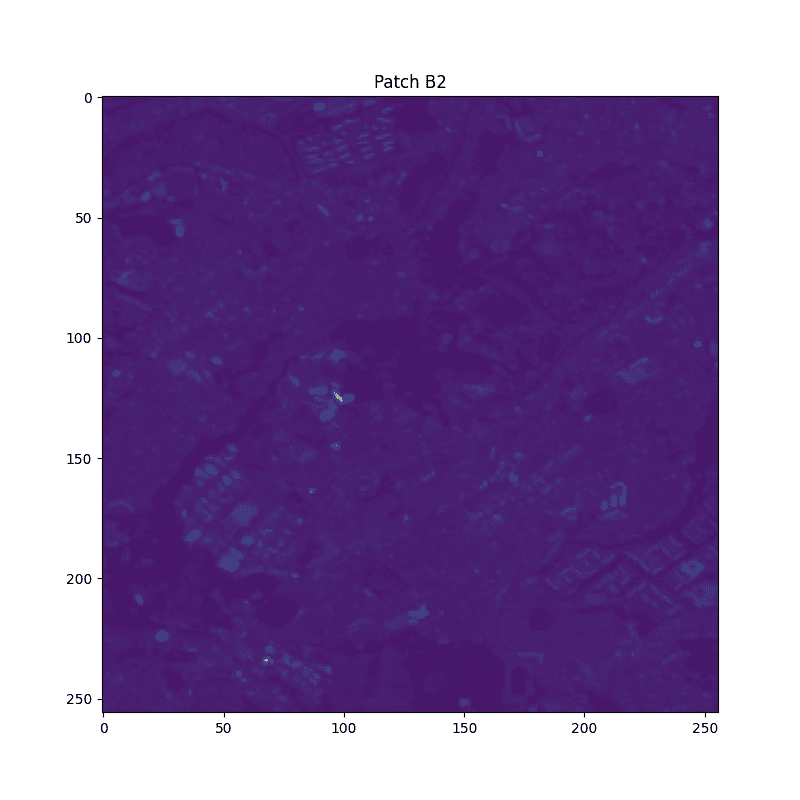
plt.imshow(patch[:, :, -1])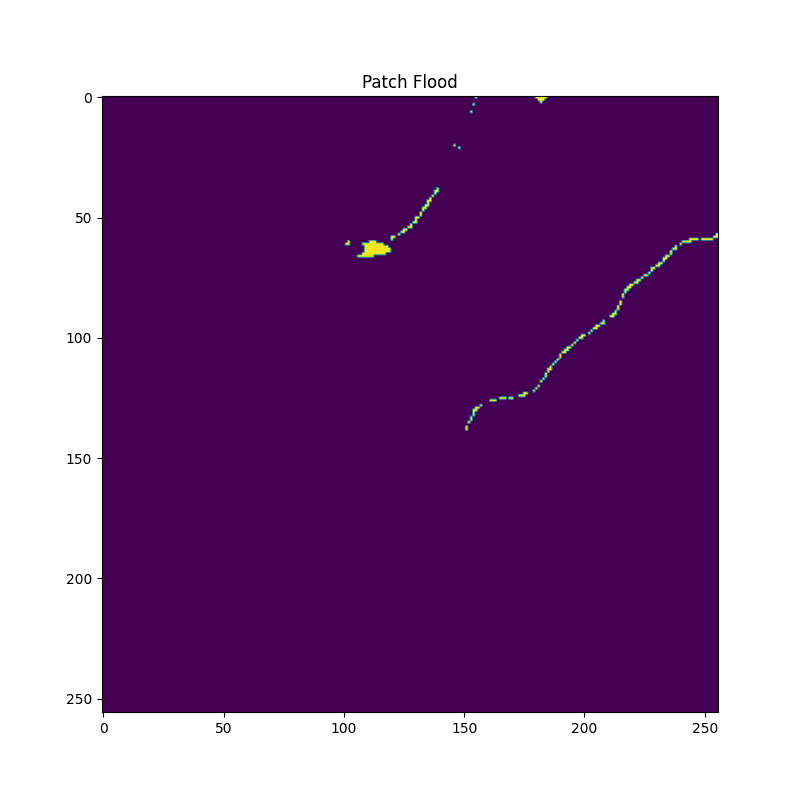

川のような場所が正しく水面判定されていますね。

学習するための処理とオーギュメンテーションを定めます。

class DataTransform():
    def __init__(self):
        self.data_transform = {
            "train": A.Compose(
                [
                  A.HorizontalFlip(p=0.5),
                  A.VerticalFlip(p=0.5),
                  A.Transpose(p=0.5),
                  ToTensorV2()
                ]
            ),
            "val": A.Compose(
                [
                  ToTensorV2(),
                ]
            )
        }


    def __call__(self, phase, img, anno_class_img):
        return self.data_transform[phase](image=img, mask=anno_class_img)


class FloodDataset(Dataset):
    def __init__(self, img_list, phase, transform):
        self.img_list = img_list
        self.phase = phase
        self.transform = transform


    def __len__(self):
        return len(self.img_list)


    def __getitem__(self, index):
        return self.pull_item(index)


    def pull_item(self, index):
        image_file_path = self.img_list[index]
        features = np.load(image_file_path)
        img, anno = features[:,:,:3], features[:,:,-1]
        
        img_and_anno = self.transform(self.phase, img, anno)
        img = img_and_anno["image"]
        anno = img_and_anno["mask"]


        return img, anno

そして、精度確認のために、学習と検証に分けていきます。
そのために管理するデータフレーム(表)を作成します。

df = pd.DataFrame({
    'depth': patch_depths,
    'h': patch_hs,
    'w': patch_ws,
    'path': patch_paths
})
df.head()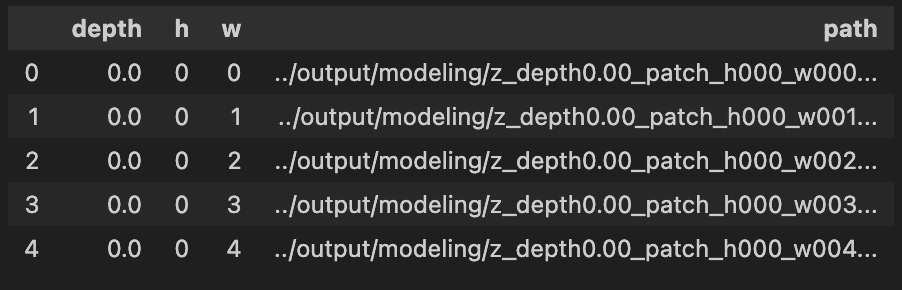

撮像シーン全体のパッチ枚数を確認します。

df.h.unique().max(), df.w.unique().max()

出力結果：(31, 38)

全体が縦31タイルなので、26〜31タイルを検証データにします。
図で示すと、下の方の部分です。

IDX_SPLIT, BATCH_SIZE = 26, 32
PATHS_TRAIN = df[df['h'] = IDX_SPLIT]['path'].values
print(PATHS_TRAIN.shape, PATHS_VALID.shape)

train_dataset = FloodDataset(PATHS_TRAIN, phase="train", transform=DataTransform())
val_dataset = FloodDataset(PATHS_VALID, phase="val", transform=DataTransform())

train_dataloader = DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=True)
val_dataloader = DataLoader(val_dataset, batch_size=BATCH_SIZE, shuffle=False)

dataloaders_dict = {"train": train_dataloader, "valid": val_dataloader}

学習データは 4万枚で、検証データは１万枚弱と重複もありますが、量だけは十分です。

モデルは UNet のバックボーンが EfficientNet b0です。損失関数はバイナリクロスエントロピーで、最適化法はAdamW で学習率が 1e-4 と基本構成にします。

model = smp.Unet(
    encoder_name='timm-efficientnet-b0',
    encoder_weights='imagenet',
    in_channels=3, # RGB
    classes=1,
    activation=None,
)


loss_fn = torch.nn.BCEWithLogitsLoss()
optimizer = torch.optim.AdamW([dict(params=model.parameters(), lr=1e-4), ])

では学習ループを回していきます。

EPOCHS = 10
best_score = 1E6


train_loss = []
valid_loss = []


model = model.cuda()


for i in tqdm(range(0, EPOCHS)):
  loss_epoch = []


  for phase in ['train', 'valid']:
    print(f'Epoch: {i} Phase {phase}')
    for (img, anno) in tqdm(dataloaders_dict[phase]):
      img, anno = img.cuda(), anno.cuda()


      if phase == 'train':
        model.train()
        output = model(img)
        loss = loss_fn(output.squeeze(dim=1), anno.squeeze(dim=1))
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        loss = loss.cpu().detach().numpy()
        
      else:
        with torch.no_grad():
          model.eval()
          output = model(img)
          loss = loss_fn(output.squeeze(dim=1), anno.squeeze(dim=1))
          loss = loss.cpu().numpy()


      loss_epoch.append(loss)


    if phase == 'train':
      train_loss.append(np.array(loss_epoch).mean())
    else:
      loss_mean = np.array(loss_epoch).mean()
      valid_loss.append(loss_mean)
      
      torch.save(model, os.path.join("../output/weights/", f'model_epoch{i}.pth'))
      
      if best_score > loss_mean:
          best_score = loss_mean
          
          torch.save(model, os.path.join("../output/weights/", 'best_model.pth'))
          print('Model saved')

評価指標として Loss を見ていきます

plt.plot(np.array(train_loss), label='train', color='blue')
plt.plot(np.array(valid_loss), label='valid', color='orange')
plt.legend()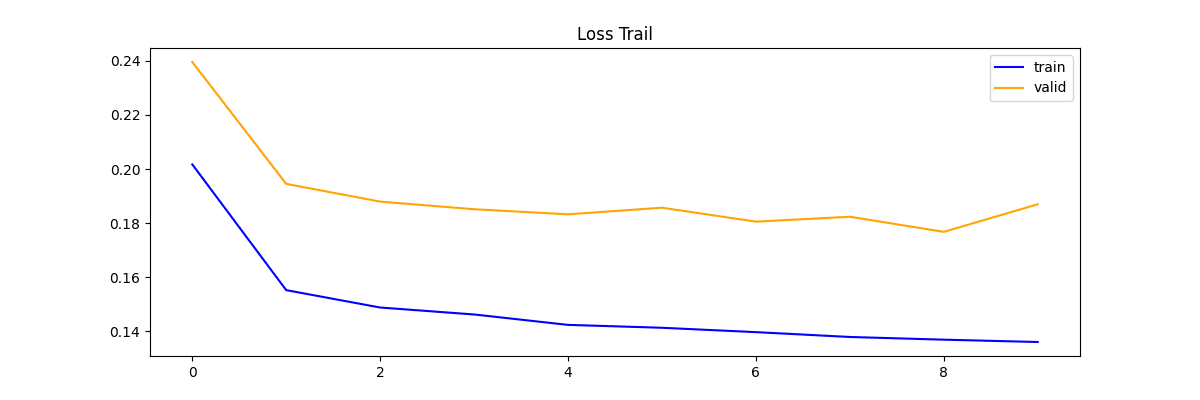

それぞれで注目していきます。
学習時の推移です。

plt.plot(np.array(train_loss), label='train', color='blue')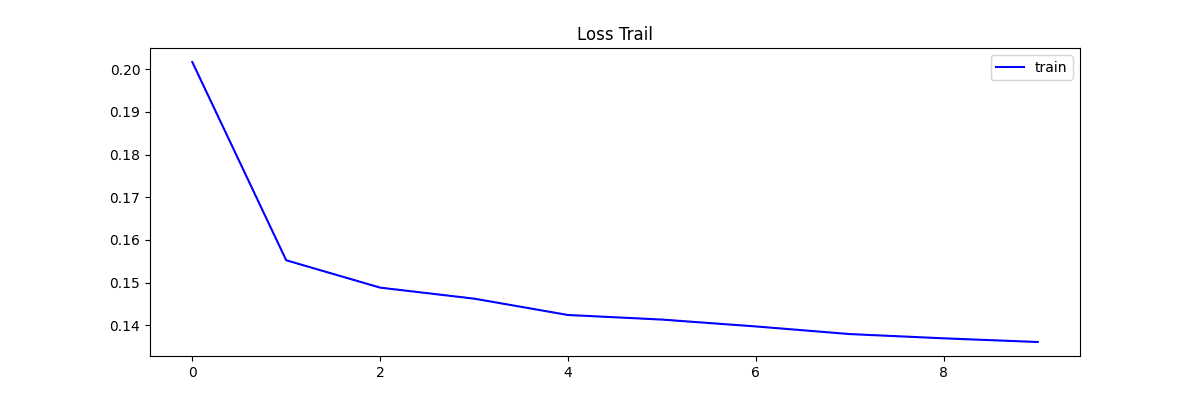

検証時の推移です。

plt.plot(np.array(valid_loss), label='valid', color='orange')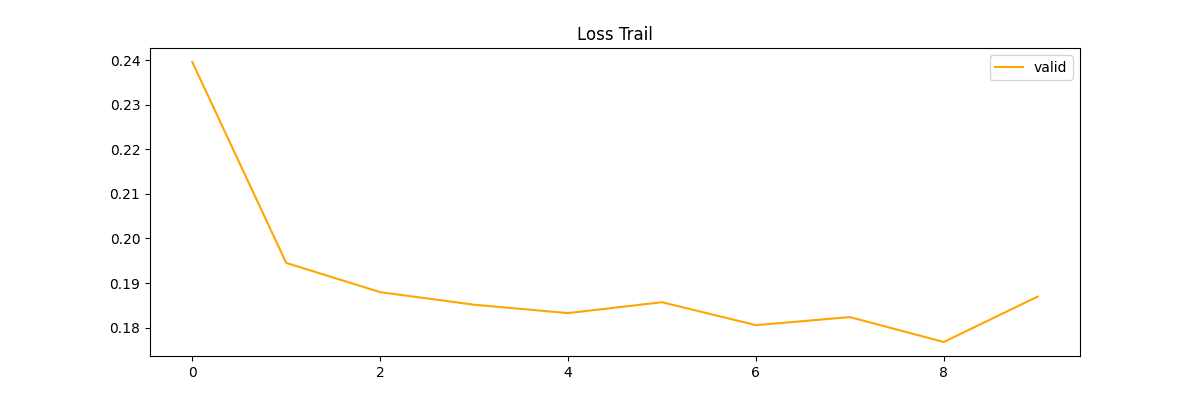

検証も下がっているので順調に学習できている推移ですね。

いよいよ、できたモデルで推論していきます。

depth, th = 11.0, 0.5


PATH = f'../output/virtual_flood/flood_{flood_depth:.2f}.tif'
img = tifffile.imread(PATH).astype(np.float32)


preprocesser = A.Compose([ToTensorV2(),])
model.eval()


features = [img[:, :, 0], img[:, :, 1], img[:, :, 2], (gt  th).astype(np.float32)
      
      prediction[h*IMG_SIZE:(h+1)*IMG_SIZE, w*IMG_SIZE:(w+1)*IMG_SIZE] = pred

予測確率の可視化をします。

PATH = f'../output/virtual_flood/flood_{flood_depth:.2f}.tif'
img = tifffile.imread(PATH).astype(np.float32)


plt.figure(figsize=(20, 16))
ax = plt.axes()
plt.imshow(img[:, :, 0], vmax=3000, cmap='gray', alpha=0.7)
plt.imshow(prediction, alpha=0.7, cmap='jet', vmin=0, vmax=1)


bbox = ((IMG_SIZE * 0 + 1, IMG_SIZE * IDX_SPLIT + 1), (IMG_SIZE * (df.w.unique().max() + 1) - 1, IMG_SIZE * (df.h.unique().max() + 1) - 1))


p = patches.Rectangle(xy=(
    bbox[0][0], bbox[0][1]
    ), 
        width=bbox[1][0] - bbox[0][0], 
        height=bbox[1][1] - bbox[0][1]
        , color='green', fill=False)
ax.add_patch(p)


plt.colorbar(shrink=0.5)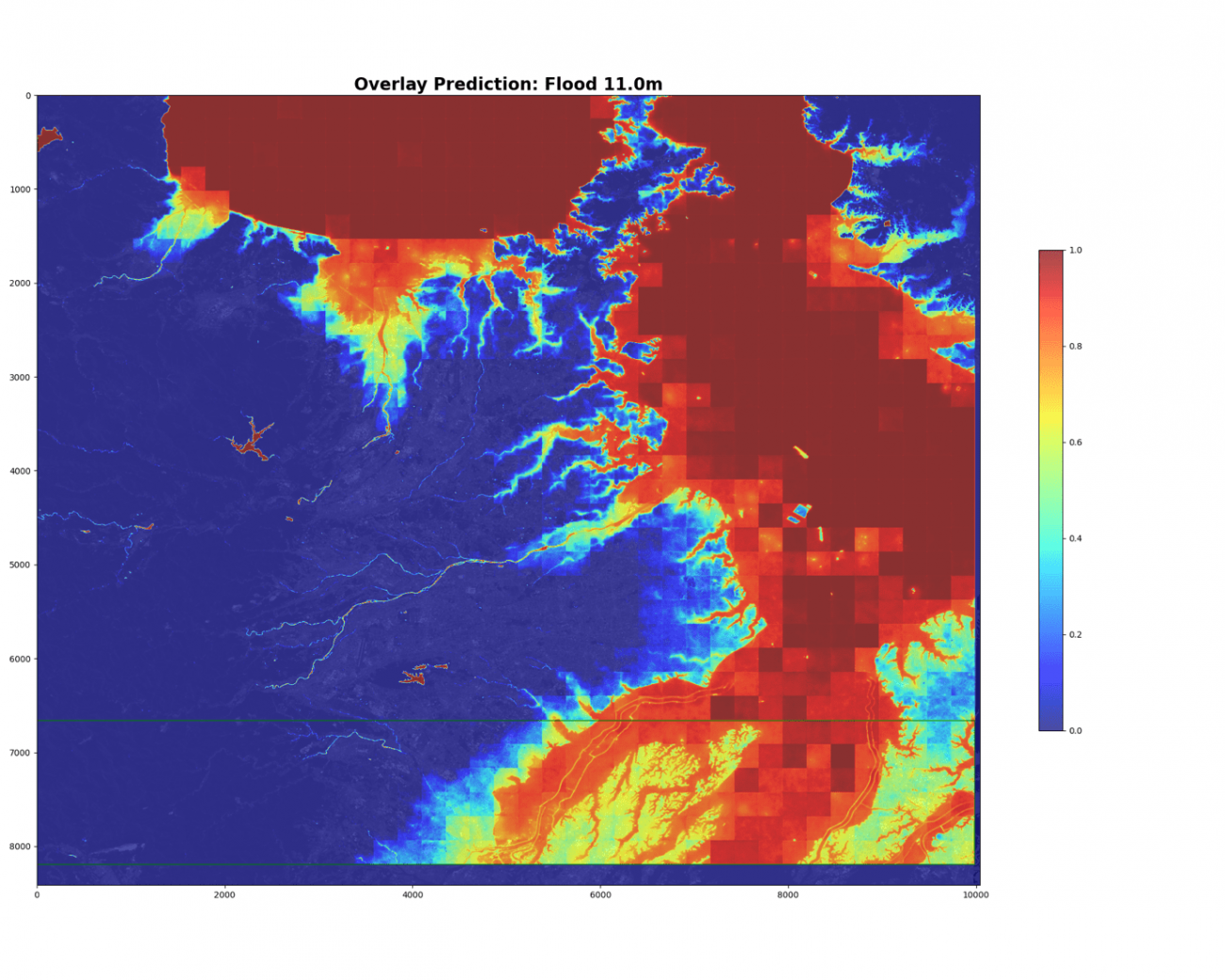

下部の緑色の枠が検証データのエリアです。
モデルは2値の確率分布を予測していて、確かに浸水域である仮想海面のエリアが赤くなっています。分類のために、確率60％で2値化します。

TH = 0.6


prediction_bin = (prediction > TH).astype(np.float32)


PATH = f'../output/virtual_flood/flood_{flood_depth:.2f}.tif'
img = tifffile.imread(PATH).astype(np.float32)


plt.figure(figsize=(20, 16))


ax = plt.axes()
ax.set_title(f'Overlay Prediction Binary: Flood {depth}m', fontsize=20, fontweight='bold')
plt.imshow(img[:, :, 0], vmax=3000, cmap='gray', alpha=0.7)
plt.imshow(prediction_bin, alpha=0.7, cmap='bwr', vmin=0, vmax=1)


bbox = ((IMG_SIZE * 0 + 1, IMG_SIZE * IDX_SPLIT + 1), (IMG_SIZE * (df.w.unique().max() + 1) - 1, IMG_SIZE * (df.h.unique().max() + 1) - 1))


p = patches.Rectangle(xy=(
    bbox[0][0], bbox[0][1]
    ), 
        width=bbox[1][0] - bbox[0][0], 
        height=bbox[1][1] - bbox[0][1]
        , color='green', fill=False)
ax.add_patch(p)


plt.colorbar(shrink=0.5)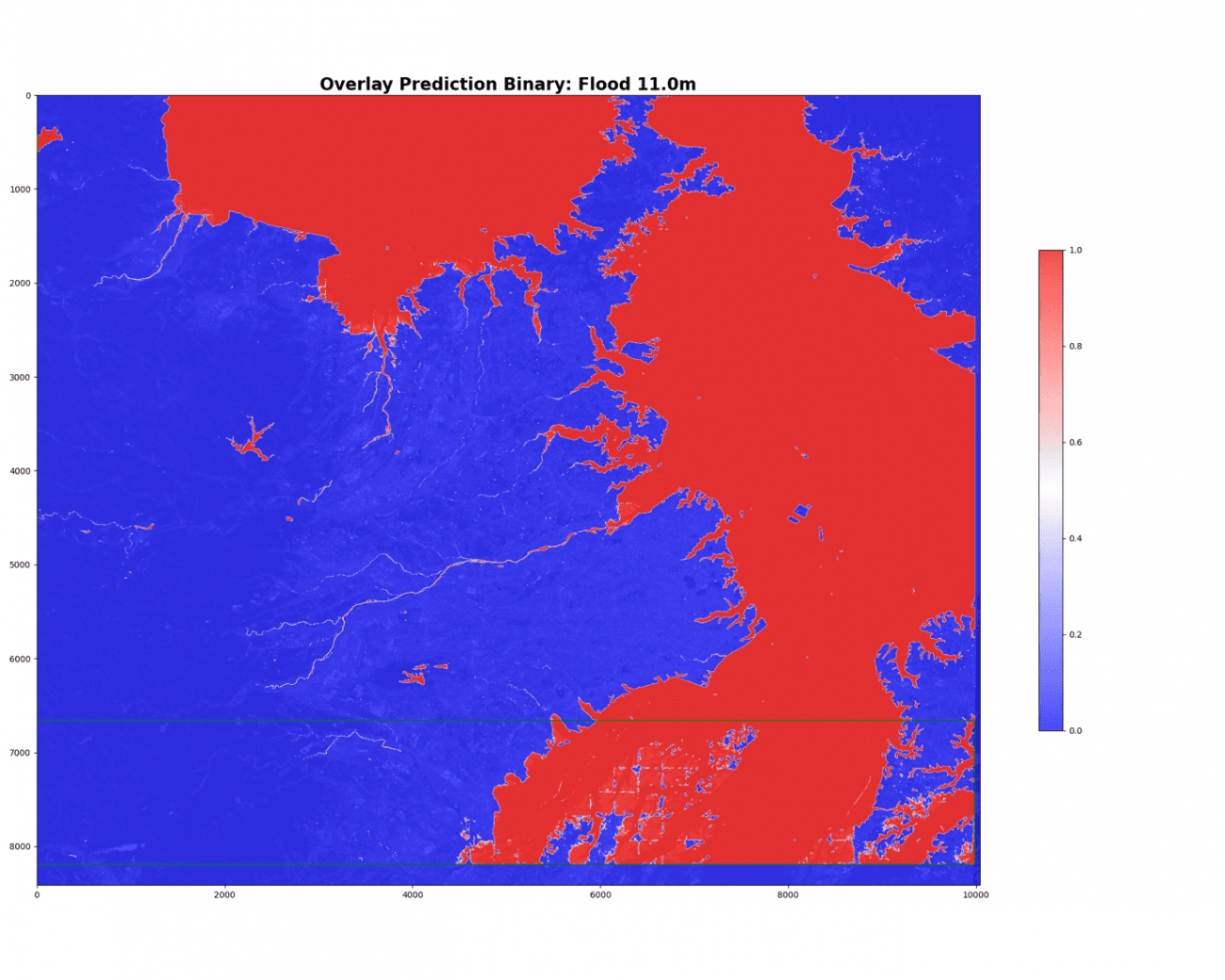

埼玉周辺の複雑な地形には苦戦しているようです。

正解と比較するために、DEMの教師データを見ていきましょう。

plt.figure(figsize=(20, 16))


ax = plt.axes()
plt.imshow(img[:, :, 0], vmax=3000, cmap='gray', alpha=0.7)
plt.imshow(gt_bin, alpha=0.4, cmap='spring', vmin=0, vmax=1)


bbox = ((IMG_SIZE * 0 + 1, IMG_SIZE * IDX_SPLIT + 1), (IMG_SIZE * (df.w.unique().max() + 1) - 1, IMG_SIZE * (df.h.unique().max() + 1) - 1))


p = patches.Rectangle(xy=(
    bbox[0][0], bbox[0][1]
    ), 
        width=bbox[1][0] - bbox[0][0], 
        height=bbox[1][1] - bbox[0][1]
        , color='green', fill=False)
ax.add_patch(p)


plt.colorbar(shrink=0.5)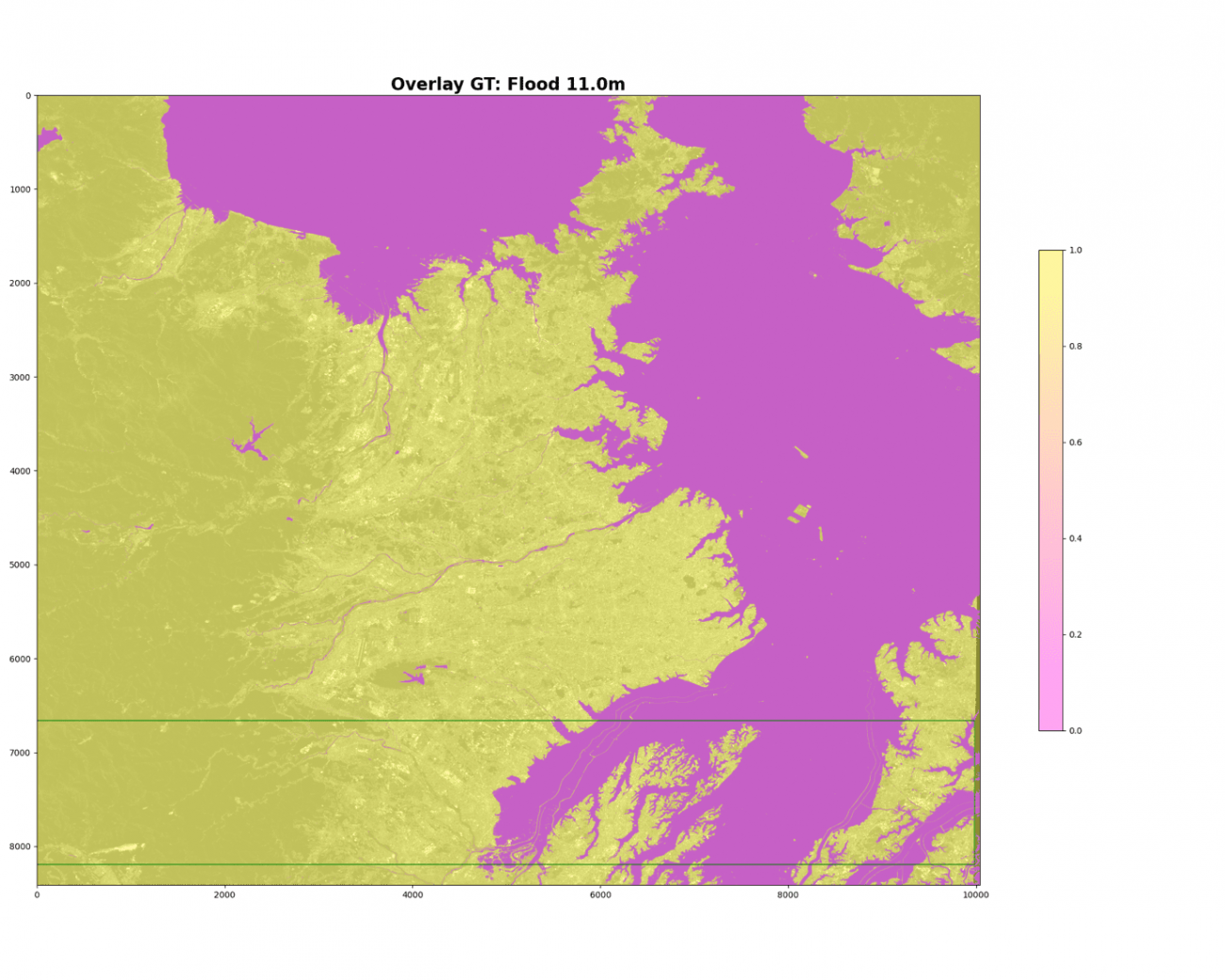

浸水深予測

浸水域が予測できたので、仮想海面との境界がわかったことになります。これは、水面（ゼロポテンシャル面とする）が平らであると仮定すれば、境界のピクセル値は仮想海面の上昇幅、即ち実データの浸水深がわかります。その原理でDEM から各ピクセルの浸水深も計算できることになります。

では、境界を検出します。

prediction_bin_canny = cv2.Canny((prediction_bin * 255).astype(np.uint8), 10, 250)


plt.figure(figsize=(20, 16))


ax = plt.axes()
ax.set_title(f'Overlay Edge: Flood {depth}m', fontsize=20, fontweight='bold')
plt.imshow(img[:, :, 0], vmax=3000, cmap='gray', alpha=0.7)
plt.imshow(prediction_bin_canny, alpha=0.7, cmap='PuOr', vmin=0, vmax=1)


bbox = ((IMG_SIZE * 0 + 1, IMG_SIZE * IDX_SPLIT + 1), (IMG_SIZE * (df.w.unique().max() + 1) - 1, IMG_SIZE * (df.h.unique().max() + 1) - 1))


p = patches.Rectangle(xy=(
    bbox[0][0], bbox[0][1]
    ), 
        width=bbox[1][0] - bbox[0][0], 
        height=bbox[1][1] - bbox[0][1]
        , color='green', fill=False)
ax.add_patch(p)


plt.colorbar(shrink=0.5)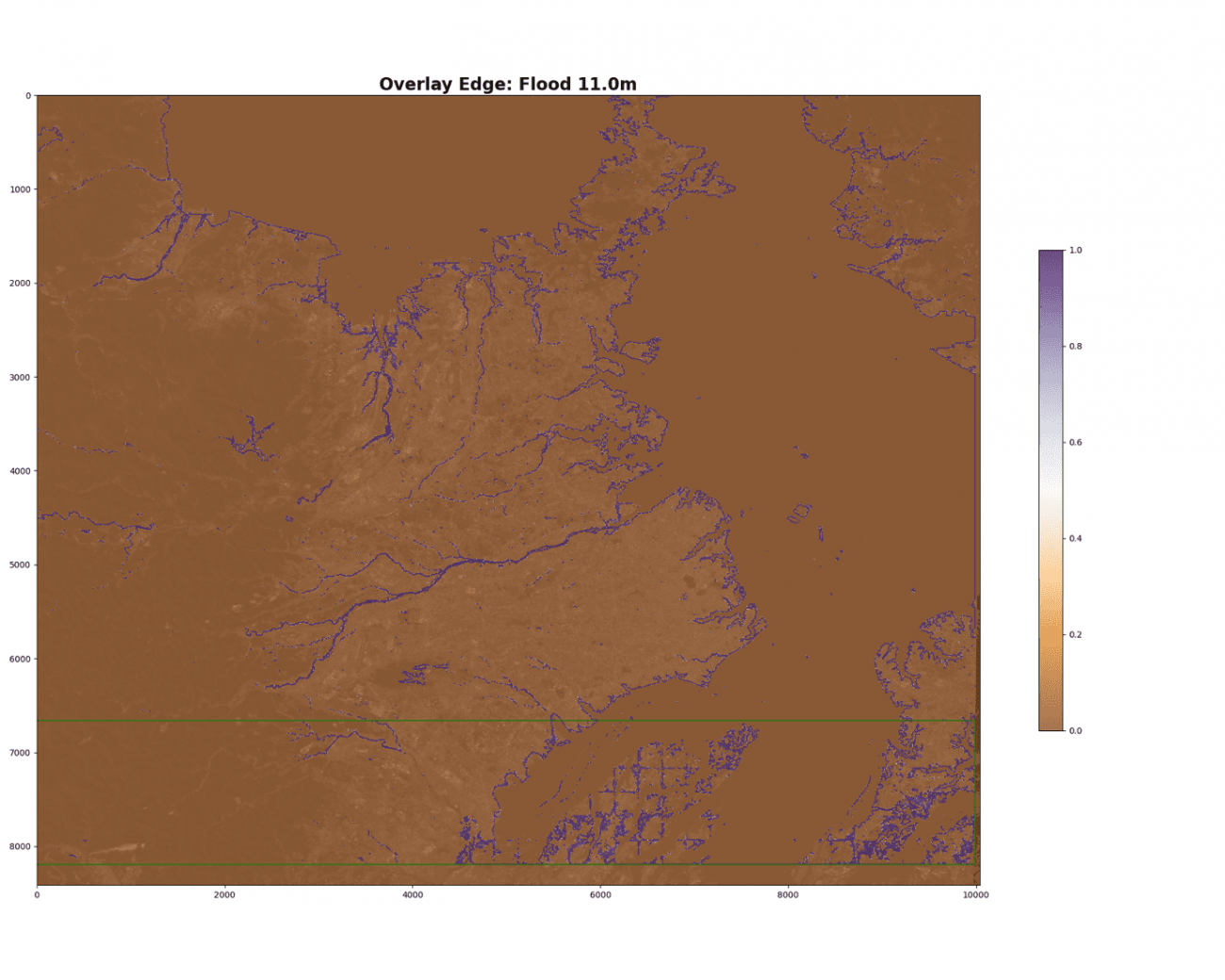

そして、境界のDEMのピクセル値の分布を見ていきましょう。

boundry_points_dem = gt[prediction_bin_canny > 0.5]


boundry_median, boundry_mean = np.median(boundry_points_dem), np.mean(boundry_points_dem)
print(boundry_median, boundry_mean)


n, bins, patchs = plt.hist(boundry_points_dem, bins=100, color='blue', label='boundry value', range=(0, 40))


mode_top = np.argmax(n)
boundry = bins[mode_top]


plt.vlines(boundry_median, 0, 20000, color='red',   label=f'Median:   {boundry_median:.2f}m')
plt.vlines(boundry_mean, 0, 20000, color='magenta', label=f'Mean:     {boundry_mean:.2f}m')
plt.vlines(boundry, 0, 20000, color='green',        label=f'Mode Top: {boundry:.2f}m')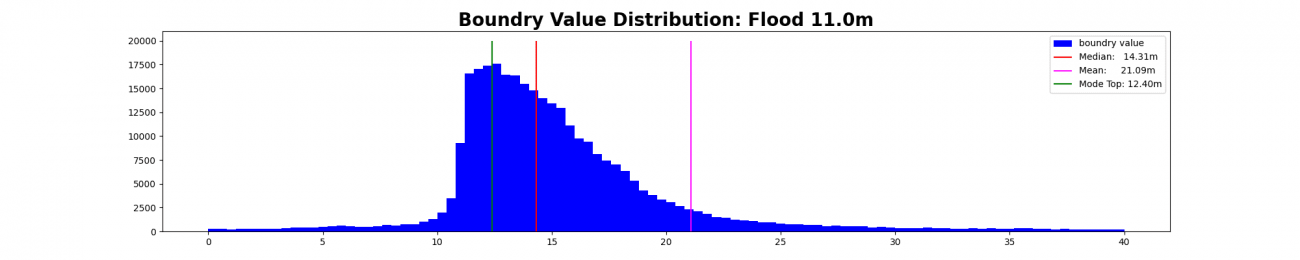

シミュレーションした海面上昇は11メートルに対して、分布のピークでは12.4メートルという予測になっています。予測誤差は1.4メートルです。

体感で実運用を考えると、50センチの誤差レベルでないと厳しいでしょう。モデルを大きくしたり、重複を削除したりより正確なモデルを作っていきたいところです。

これだけでは正しい検証とは言えないので、衛星の実画像で検証する必要はあります。しかしながら全く当てにならないわけではなく、シミュレーションデータで事前学習をして転移学習や、ファインチューングする際に実験の高速化、精度の安定化にも繋げられるからです。どんな武器でも使う人次第です。

続いて、モデルの浸水予測確率を出したので衛星データとレイヤーで重ねてみましょう。

各市区町村で配布されている防災マップの津波被害エリアと似たようになるはずです。ほとんどのマップがDEMを学習しているからです。

2値分類も重ねてみます。

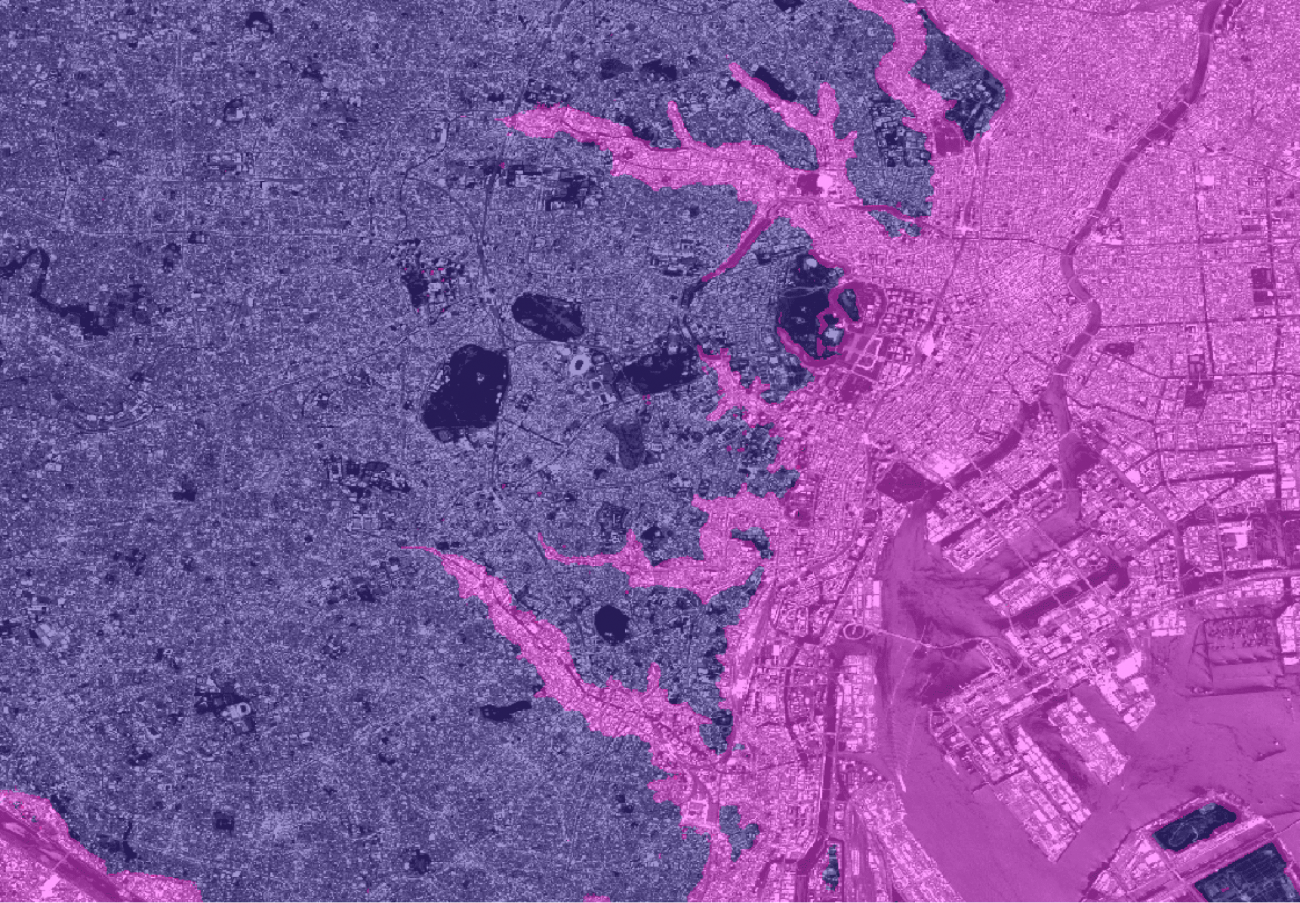
意外と河川が低いところばかりではないようです。標高は洲などの地質学的な地形の知見も絡んできます。

海岸線検知もできそうですね。DEMがある場所はDEMで定まりますが、国土管理がまだ整備されていない海外では有効かもしれません。

神奈川の岬の方は幾何学的になっていますね。具体的には、フラクタル図形のマンデルブロ集合です。

浸水予測との組み合わせ

続いて、浸水と関連がありそうなデータとの可視化を行っていきます。

まずは、PLATEAU(https://www.mlit.go.jp/plateau/open-data/)の避難ルートと避難シェルターのプロットです。

凡例(浸水確率：赤、避難ルート：ピンク、避難シェルター：緑)

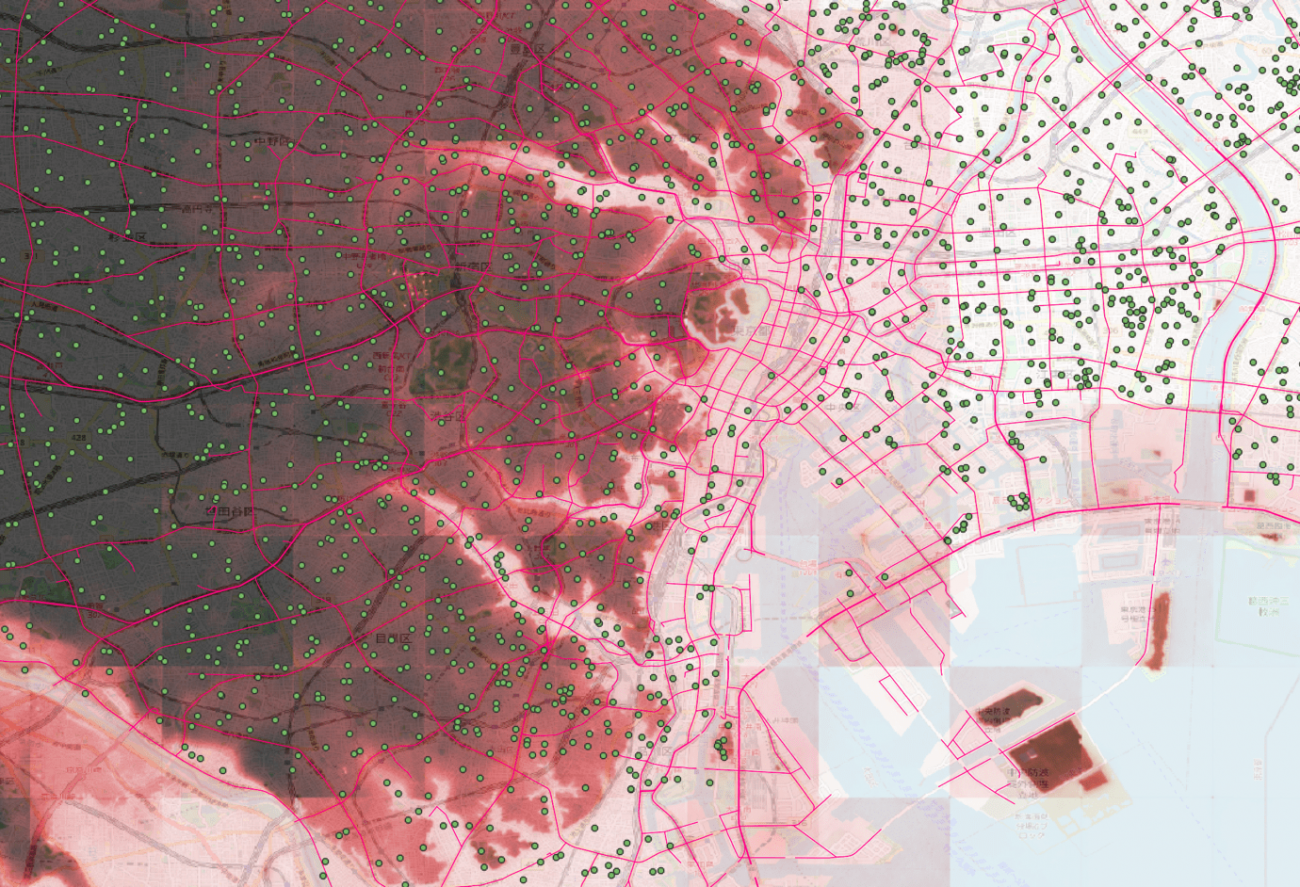
最寄りの避難場所でしたり、高い建物が設定されているためなのか、低い浸水被害に合いそうな場所にも多く見られます。避難ルートも同様に大通りの低い土地が多いことがわかります。

Microsoft(Azure)が最近は宇宙領域に力を入れてきています。そのサービスとして Planetary Computerがあります。そこでは、衛星データやそれらに関連する情報を提供しています。

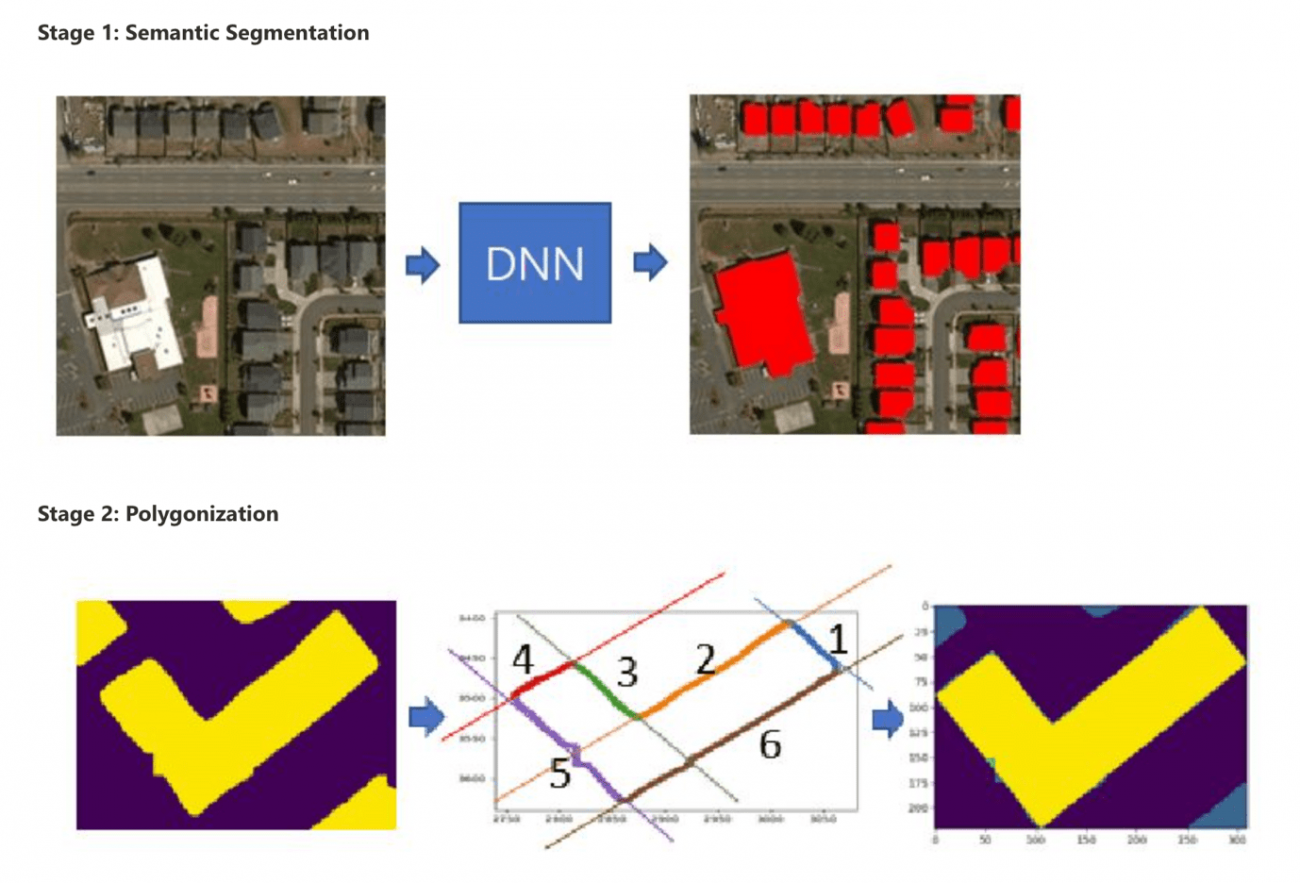
その１つに全世界の建物の外型の予測結果のポリゴン情報を公開し始めました。
https://planetarycomputer.microsoft.com/dataset/ms-buildings#overview

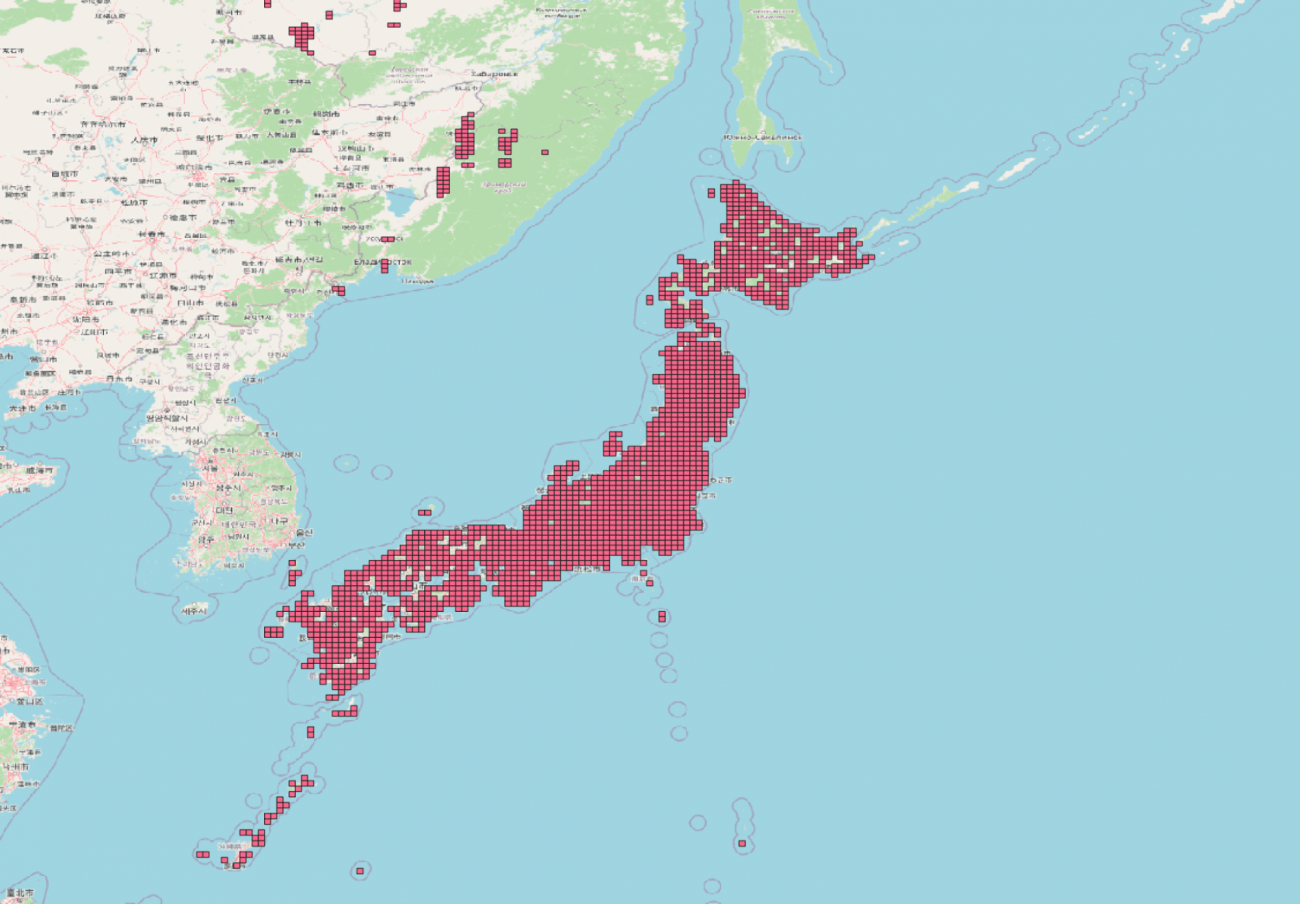
日本も公開エリアに含まれていますが執筆段階（2023/06/16）では、まだ公開されていないです。そのため、アメリカのアルバータ州の建物ポリゴンをお見せします。

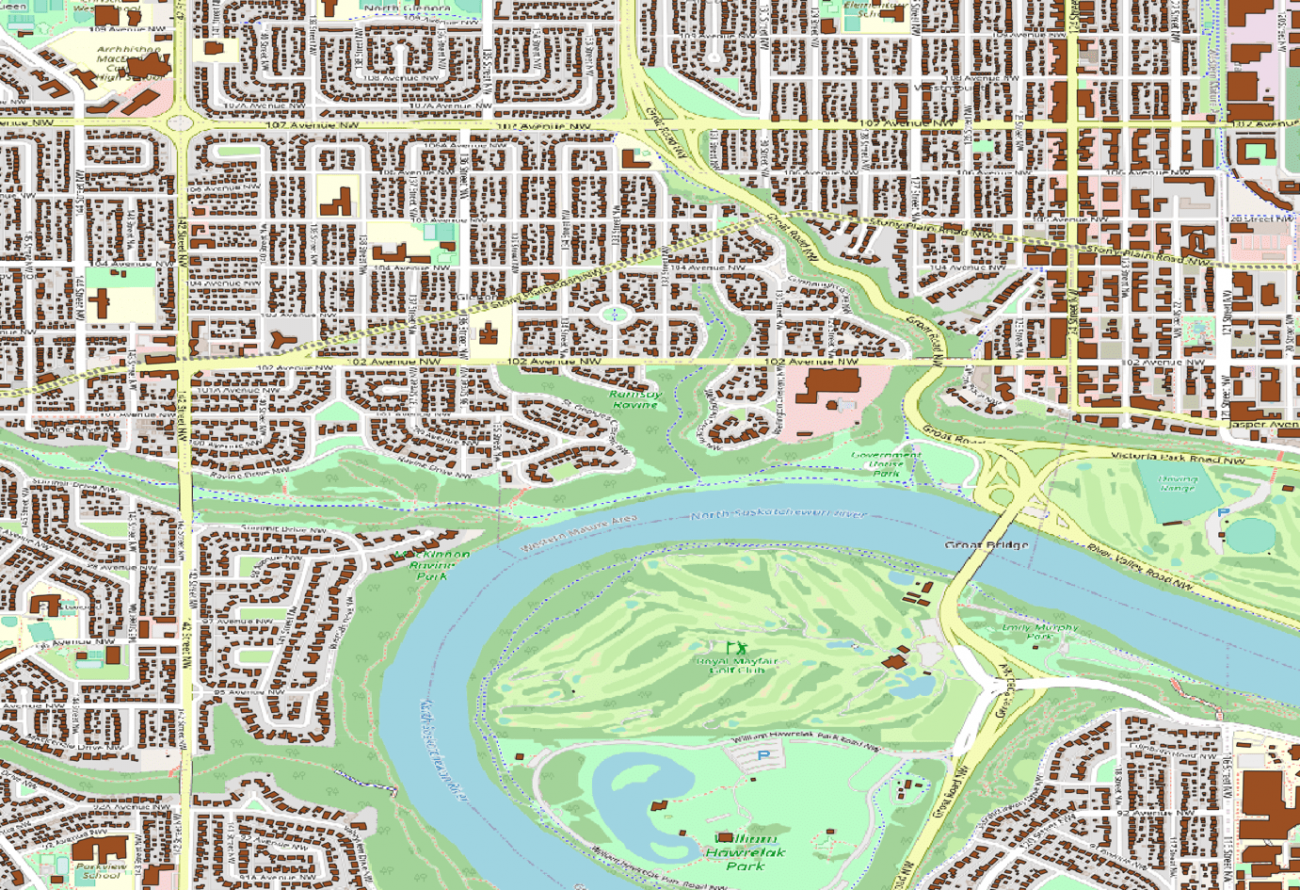
この数の建物（茶色）の情報が公開されています。この情報があれば、浸水エリアと組み合わせることで衛星の撮像から何世帯が浸水被害にあったなどの予測が可能になります。保険会社や金融産業が欲しいと思えるだろうデータです。

コードと環境

宙畑では記事に利用したデータやコードについて、読者の皆様が実践したい！と思ったときに実践できるよう、できる限り情報を整理してオープンにしています。

シミュレーションしたエリア：Sentinel Hub Sentinel-2
Github: https://github.com/sorabatake/article-32855
動作環境: https://github.com/sorabatake/article-32855/blob/main/src/000_data.ipynb

■地理空間処理について
・https://github.com/sorabatake/article_32245_gdal
・https://github.com/sorabatake/article-32855/blob/main/src/001_simulation.ipynb
・https://github.com/sorabatake/article-32855/blob/main/src/002_modeling.ipynb

■分析や予測について
https://github.com/sorabatake/article-32855/blob/main/compose.yml

また、Docker Compose + Nvidia Docker の環境が必要です。

環境構築は以下です。

docker compose up -d

http://localhost:6868/lab で JupyterLab で Notebook を実行できます。

ファイルの配置は以下の記事に従っています。

今回使用したサンプルデータや学習済みモデルは以下で取得可能なのでぜひお手元で動かしてみてください。
※実践した内容を公開などされる場合は、出典の明記などの利用規約を遵守いただくようお願いいたします。
https://drive.google.com/drive/folders/12u8zH6-7kVcOcKi-oeaDw53AeSxOJUOg

記事の内容を実践してみて、エラーが出た場合は、こちらのGoogleフォームにエラー内容のログを全てと改修したいことをリクエストいただけますと幸いです。
⇒エラー発見&改善リクエストはこちら

まとめ

本記事では、DEMと衛星データを用いた洪水がこれまで起きていない土地における教師データとなりうる洪水シミュレーションデータの作成方法を紹介しました。また、本記事では作成した教師データを用いた解析の実践と、その他衛星データ以外との重ね合わせについても紹介しています。

Githubにコードも掲載しておりますので、各自治体、個人、企業で自由にご利用ください。

そもそも予測が必要な被害がでないことが理想ではありますが、今後、自然災害が様々な場所で発生した際により速く、正確に被害状況を把握できるための一助と本記事がなれますと幸いです。