成功!!複素ニューラルネットワーク(CxNN)を実装して衛星データから物体検出をしてみる
単なる画像としてではなく、電波の位相情報も取り扱うために複素ニューラルネットワークを用いて、SARデータの物体検出を行います。
宙畑では、これまで衛星データと機械学習をテーマに様々なトピックを紹介してきました。
人工衛星の費用の低下や、様々な宇宙ベンチャーの参入に伴い、衛星データが爆発的に増えてきており、人の目では処理しきれなくなって来ているため、機械学習の適用が望まれています。
現在、機械学習の技術が適用されている衛星データ解析事例の多くは、衛星データを単なる画像データの一つと捉え、物体検出や画像分類などを行っています。
この分野はこれだけでも非常に適用範囲が広く、今伸びている領域ですが、衛星データの中でも電波による観測をしているSARデータは「波」の性質に紐づく情報などが含まれており、元のデータは単なる画像以上の情報を有しています。
したがって、衛星データの能力を最大限に引き出すためには、より踏み込んだアプローチが必要となります。
今回は、そんな単なる画像情報だけではない衛星データを、深層学習で扱う技術「複素ニューラルネットワーク」を紹介していきたいと思います。
複素ニューラルネットワークの研究は昔から行われていますが、複素情報を用いるため用途が限られており、そこまで注目されていない現状があります。しかし、衛星データとの相性は抜群なため、今回は実際に理論的な部分から実装、学習、識別までの一通りをSARデータ解析を題材に解説していきます。
本記事に出てくるコードはgithubでも公開しています。
https://github.com/sorabatake/article_18837_CxNN
複素ニューラルネットワークとは
複素ニューラルネットワークの概要
複素ニューラルネットワークとは
複素ニューラルネットワーク(CxNN: Complex-valued Neural Network)とは、一般的なニューラルネットワークの重みや計算方式を複素数に拡張したものです。複素ニューラルネットワークに対して、一般的なニューラルネットワークを「実ニューラルネットワーク」と言うことがあります。「実」は実数を意味します。
複素ニューラルネットワークの利点「周期的な運動に強い」
複素ニューラルネットワークの利点は、周期的な運動の表現力(推定精度)が増すところにあります。
具体的には、ニューラルネットワークが苦手とする「シフト移動」や「回転」等を上手く扱えるようになるということです。この強みは、電波による観測をしているSARデータを扱う上では特に重要な要素です。
以下をご覧ください。左が実ニューラルネットワークで、右が複素ニューラルネットワークです。テストデータとして一部の赤丸を与えて、再帰的に回帰させたものです。
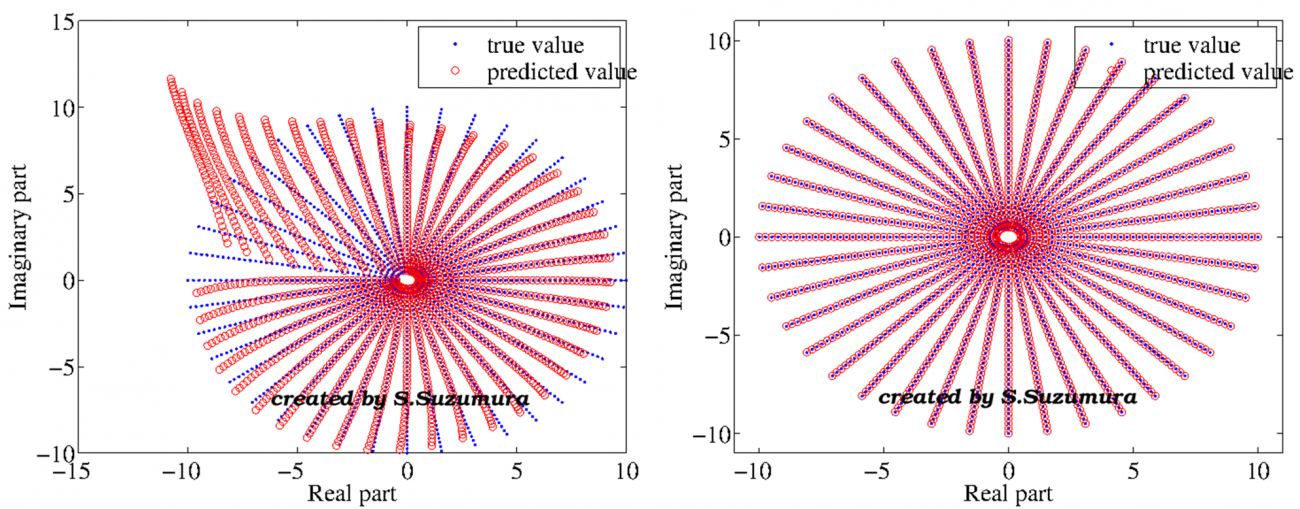
これを見ると、複素ニューラルネットワークは周期性の獲得に成功しているように思えます。これは内部構造に複素数の座標変換(後述します)制約があるため、実ニューラルネットワークより精度の高い結果になったわけです。
普遍性定理から、実ニューラルネットワークでも複素ニューラルネットワークの働きを学習によって獲得することが可能です。しかし、より多くのニューロンを消費しますし、複素数特有の(計算的な)制約が入らないため非効率な計算になります。ここに、複素ニューラルネットワークを構築する価値があります。
複素ニューラルネットワークの適用分野
複素ニューラルネットワークは周期性を使うような分野、水や音、光、振動等の「波」に関連する回帰的な解析に向いています。
分類問題における複素ニューラルネットワークの利点
さらに、複素ニューラルネットワークは回帰問題の他に分類問題を解くこともできます。
分類問題を解かせる場合も実ニューラルネットワークと比べて大きな違いがあります。それは、何度も言う周期性です。実はこの周期性、使い方によっては大きな利点になります。
良く挙げられる例はn-bit偶数パリティ―問題です。
これは、組み合わせ(ビット数)が増えると識別するのに多くのニューロンを要するという問題です。
以下のXOR問題をご覧ください。左は1セルの実ニューラルネットワークにXOR問題を解かせた例です。右は1セルの複素ニューラルネットワークにXOR問題を解かせた例です。青/橙色の点群が学習データで、背景のグラデーションが推論結果としての分離超平面(線)です。
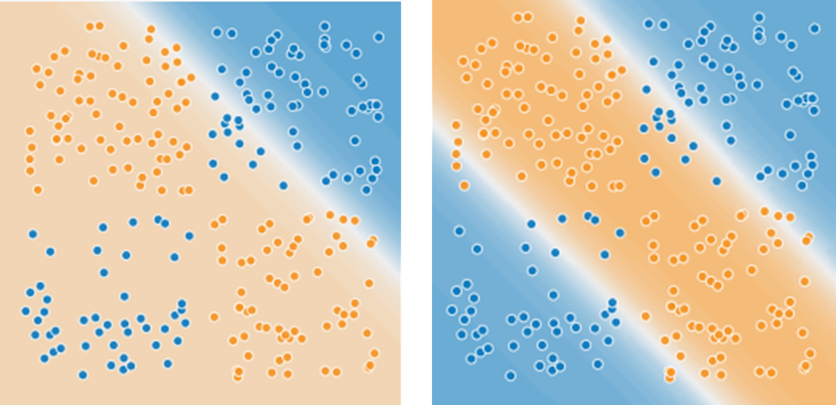
左は青/橙色の点群を上手く分離できていないのに対して、右では多少オーバーラップしてしまう箇所はありますが、上手く分離出来ているように見えます。これが、複素ニューラルネットワークの強みなのです。
なぜ、このようなことが出来るのかを説明します。複素ニューラルネットワークで分類問題を解く際は単位円上で推論を行います。例えば2値識別を行う際には以下のような単位円を描きます。

ここで青がクラス0、橙がクラス1を指しています。クラスの並びは周期性を考えて配置する必要があるので、対角線上は同じクラスになります。このクラスの並び、まさしく先ほどのXOR問題ではないでしょうか。
簡単に、4象限に2クラスが配置されていると考えればよいです。実際にこの分類問題を複素ニューラルネットワークで学習させていくと以下のように収束します。
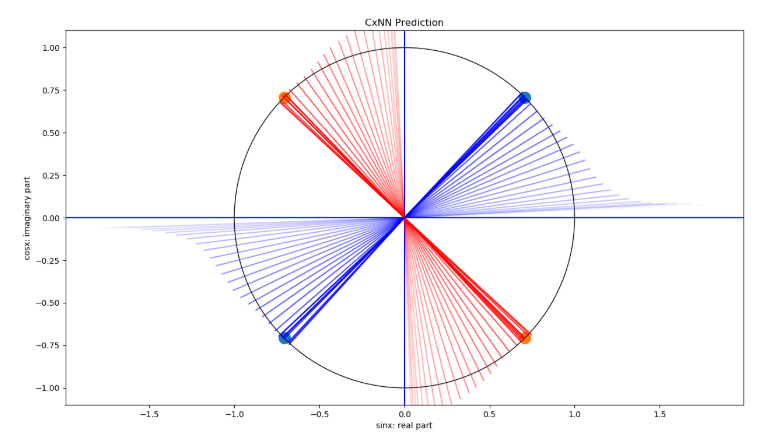
見て分かる通り、周期的に答えを学習するのです。クラス0の対角線上はクラス0ということです。位相(角度)が90度ズレるとクラス1です。この辺が実ニューラルネットワークと異なる点です。
それでは複素ニューラルネットワークの面白さを見たところで、理論的な背景に入っていきたいと思います。
【理論】複素数とは?
実数と虚数からなる複素数
複素ニューラルネットワークを構成する要素で最も重要な複素数について解説していきます。既にご存知だという方は飛ばして頂いて良いです。
2次元平面における複素数というのは、x、y変数によって表される座標を1次式で表現できるようにしたものです。すなわち、以下のような形式を複素数といいます。
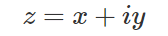
ここで各x、yは各軸の変数なので独立(複素数と)して計算されます。それを示すためにiという文字がついています。これはimagine(虚数)のiです。一方のxはreal(実数)ということになります。それぞれ、Imag/ImやReal/Re等と省略します。これは単純に2次平面(複素平面)の関係で、平面直交座標系で表すと以下のようになります。
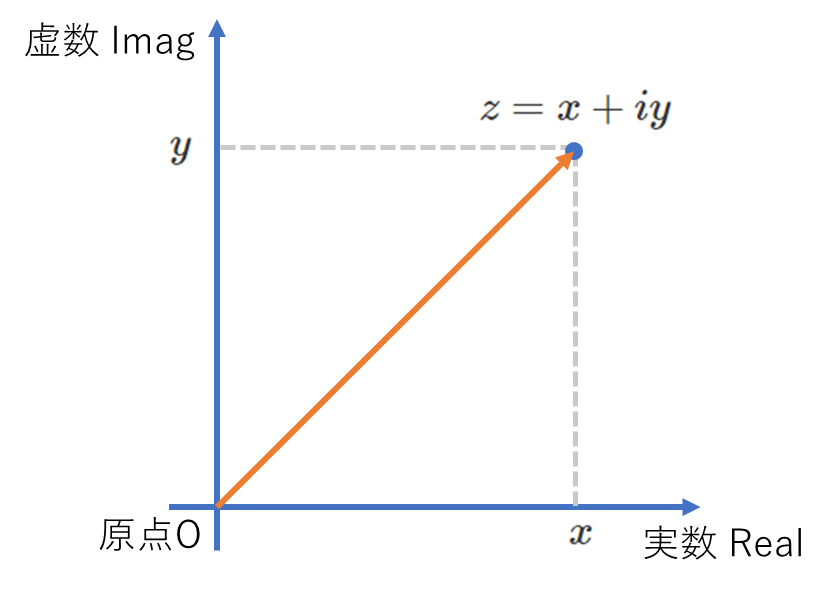
これを少し発展させ、オイラーの公式を基に偏角θを導入して三角関数との関係式を作ると各変数(x, y)は次のように対応が取れます。
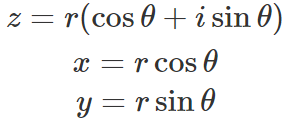
これを極座標形式と呼ばれる座標系で表すと以下のようになります。ここで、円は単位円のためr=1となるので式が見やすいようrは省略しています。

ここまでは簡単なのですが、次からが少し難解で、複素数の肝となる制約です。複素数同士の掛け算は以下の制約があります。
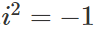
これは複素成分の虚数同士を掛け合せると-1になるということです。
座標変換(回転)としての複素数の意味
数学的な意味を考えると頭が混乱するかもしれませんが、これに数学的な意味はありません。座標変換(回転)としての制約なのです。
具体的には、
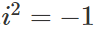
で90度の回転(象限移動)を表現できます。すなわち、i×i×i×iは-1×-1=1となり、360度の回転を表現することになります。以下にその例を示します。
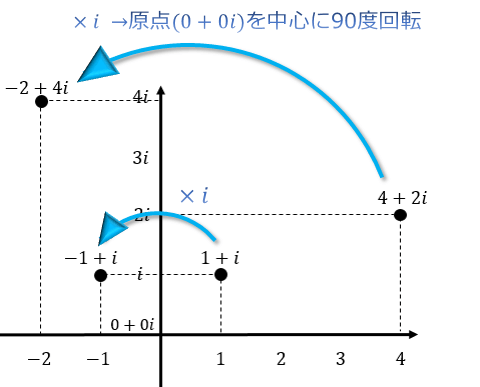
このように2次元平面における移動を1つの数式で表現できるのが複素数です。
ニューラルネットワークへの適用の下準備(複素数同士の掛け算)
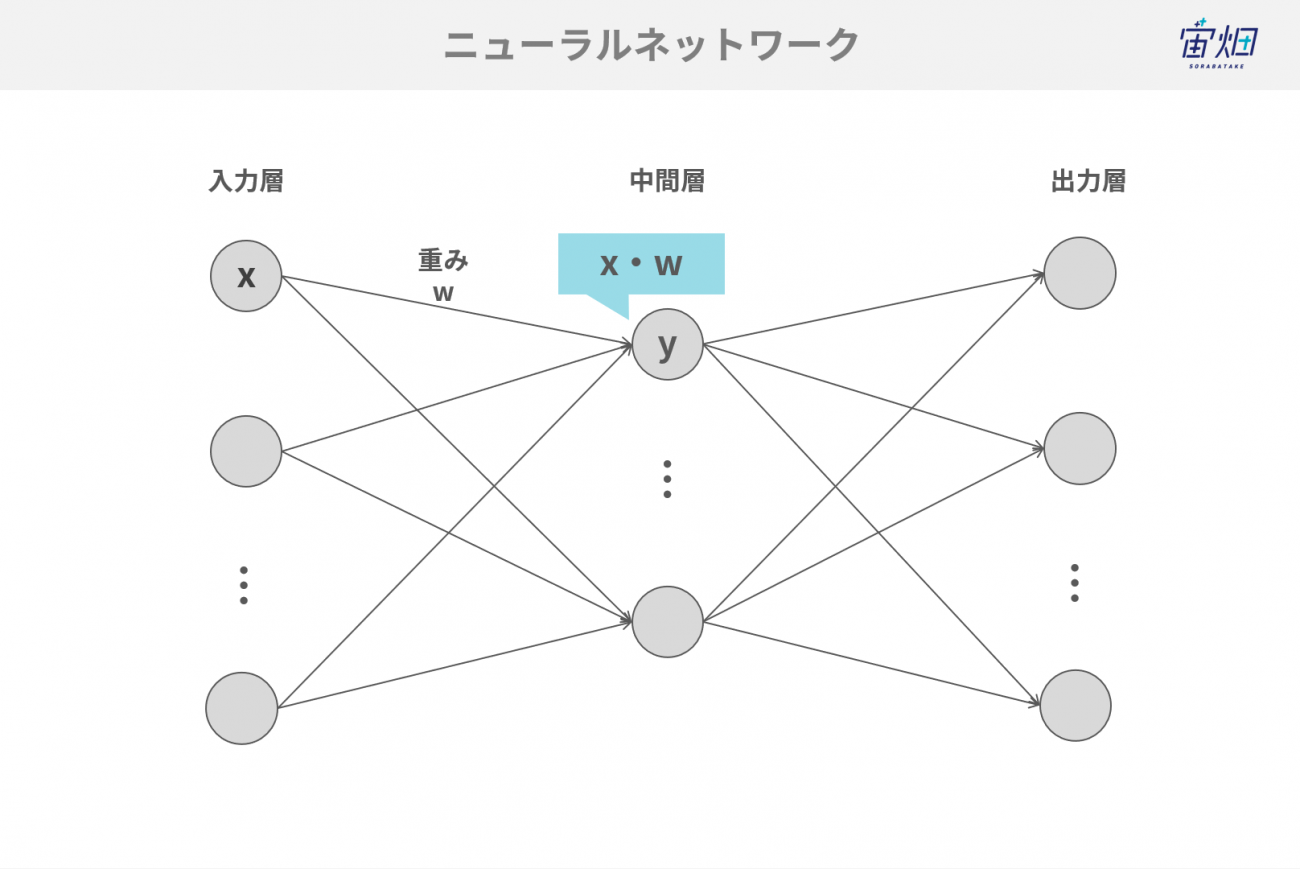
複素ニューラルネットワークは、一般的なニューラルネットワークの入力や重みが複素数に拡張されるということです。
すなわち、通常であれは入力xと重みwは単純な掛け算となりますが、複素ニューラルネットワークでは複素数同士の掛け算をすることになります。
入力が複素数のx、ニューラルネットワークの重みが複素数のwのそれぞれの実数部と虚数部を右肩にreとimを付けて、以下の様に表します。※xは座標を示す変数ではなく入力を示す変数です。
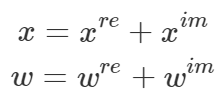
複素数同士のx, wの掛け算を展開していくと以下のようになります。
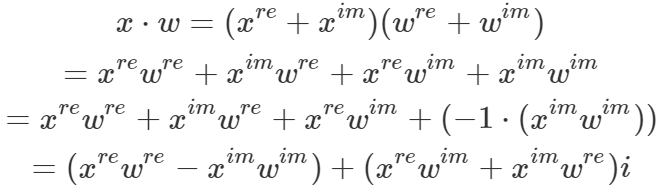
i成分がついているものが虚数成分(y軸)になります。すなわち、実数と虚数で分けると以下のようになります。
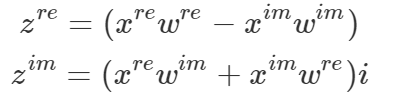
虚数を示す変数に実数が掛け算で入ってきていますが、最終的には虚数を表すものなので惑わされないようにしましょう。
【理論】-ニューラルネットワークへの適用①ニューラルネットワークの計算
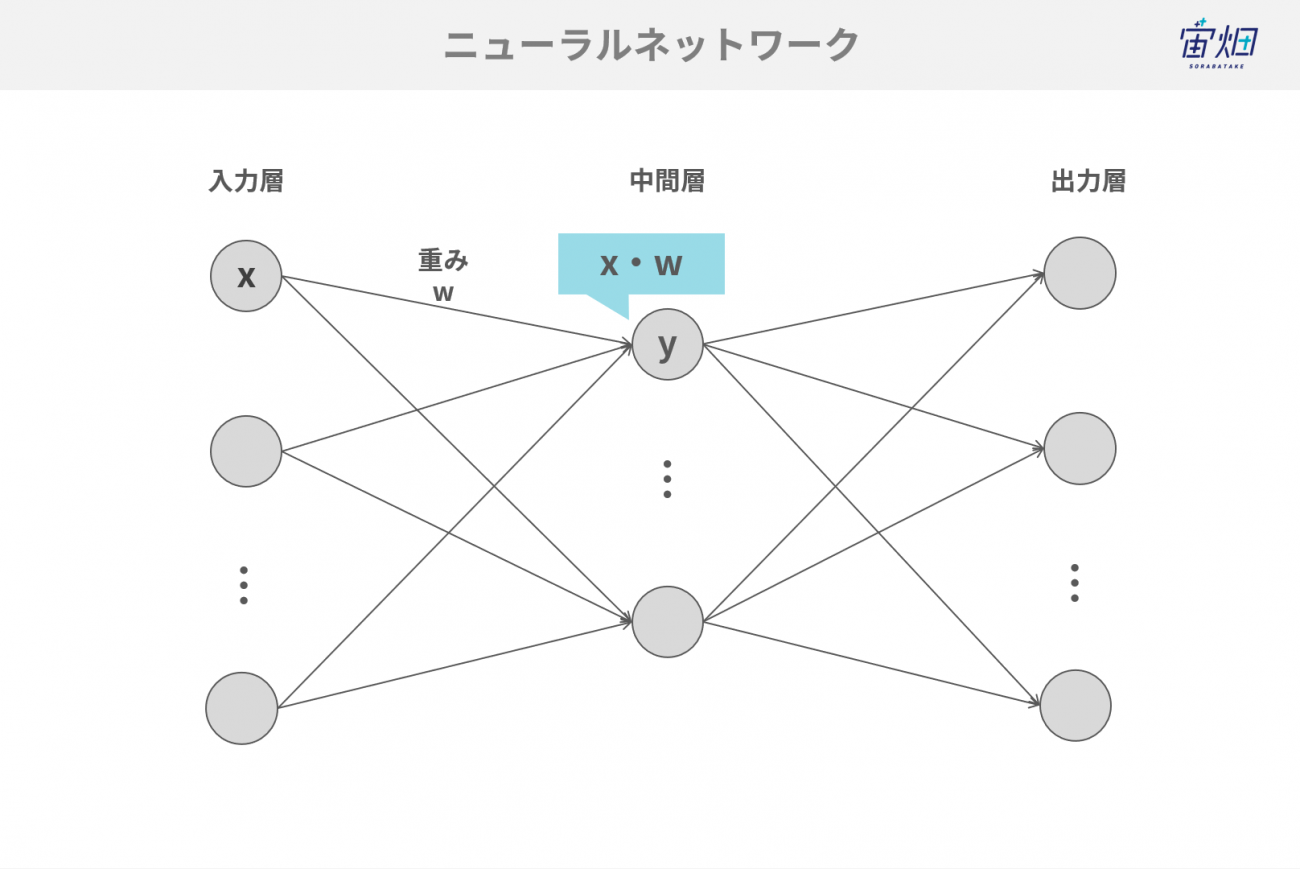
それでは先ほどの複素数をニューラルネットワークに導入します。
ニューラルネットワークの計算は、入力をx、重みをw、バイアスをbとして、以下のように線型結合の総和によって行われます。
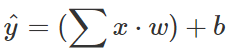
複素ニューラルネットワークにするためには、x、wを先ほど解説した「2変数の複素数の掛け算の式」に置き換えるだけです。すなわち、次のようになります。
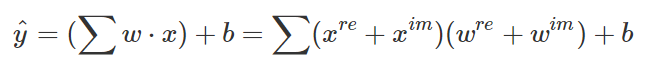
ここで、x、wは複素数になります。では、先ほど解説した通りに、この掛け算を展開していきましょう。そうすると、実数部と虚数部それぞれで、次のような2つの式が得られます。
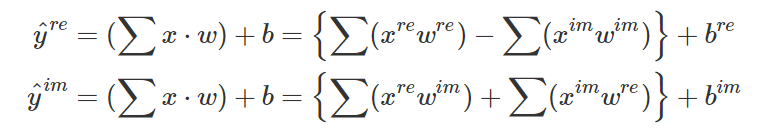
先ほど展開した式に線型結合の総和を取るシグマ記号がついただけの式となります。
これは実数と虚数を分けて書いているだけで、先ほどのこの式と殆ど同じです。
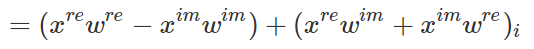
【理論】ニューラルネットワークへの適用②角度への変換と正規化
最後に、分類問題を解く際に実数と虚数を角度に変換しなおす必要があります。それは以下のように行います。
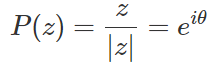
クラスの角度を単位円上で表現するため、正規化が必要になります。この正規化処理はニューラルネットワークに活性化関数として適用されます。
これで全ての道具が揃いましたので、学習データを準備し、複素ニューラルネットワークを構築して衛星データ解析を行っていきたいと思います。
複素ニューラルネットワークを適用する衛星データ
単なる画像ではない?SARデータとは
ここで複素ニューラルネットワークを適用する衛星データについて、少し説明をしておきます。

Credit : JAXA
今回使用するのはSAR(サー)データと呼ばれる衛星データです。衛星から電波を発し、地表面でその電波が跳ね返えり、衛星まで戻ってくる信号を観測します。妊婦さんのエコーの画像をイメージしていただくとよいかもしれません。
SARデータはいくつか前処理が必要です。大元のSARの生データは電波の情報です。
それをレベル1.1というSLC(Single Look Complex: シングルルック複素画像)に変換し、さらにその複素画像から戻ってきた電波の強度を示す輝度値(Intensity)及び位相(Angle)に変換し、その内から輝度値のみを取り出したものが、世間一般に言われているSAR画像です。
画像化すると、上の画像のように白黒の絵になりますが、絵にしてしまうと、電波のもう一つの要素である「位相」という情報が失われてしまいます。
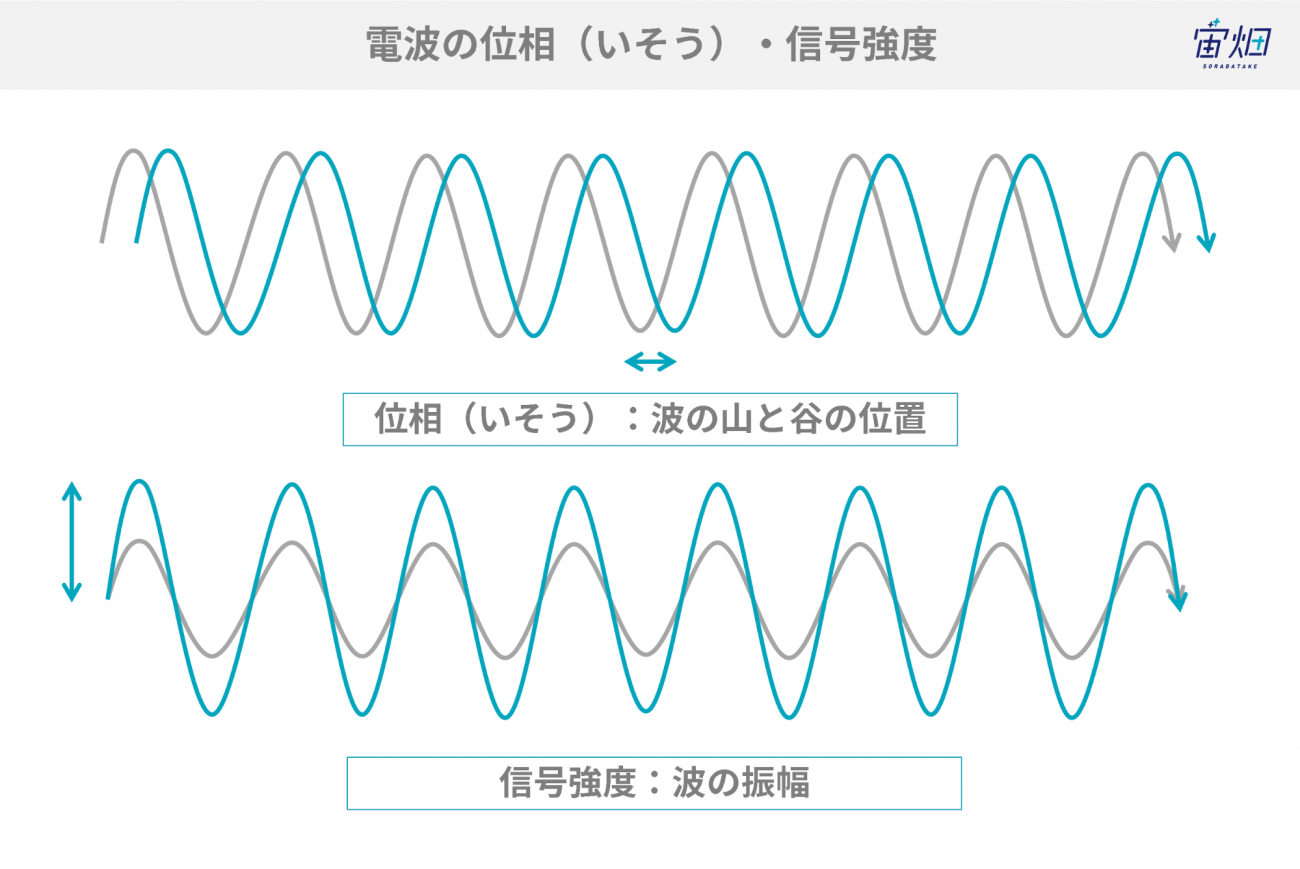
位相とは、上図で示すように波の山や谷の位置を表す言葉です。波の振幅は同じでも、山や谷の位置がずれることがありますが、画像化してしまうと、この情報が失われてしまうのです。
近年では、機械学習を使ったSAR画像解析が実施され始めていますが、強度のみの情報を使い、単なる画像として解析を行っているものが多いのが現状です。位相情報まで含めた解析ができれば、物体検出などの精度を上げることができる可能性があります。
この位相情報まで含めた解析を行うために適しているのが、前章でご紹介した「複素ニューラルネットワーク」なのです。
なお、今回は強度情報と位相情報を入力としていますが、複素ニューラルネットワークの応用範囲は非常に広く、SAR画像の各偏波画像(HH, HV, VV, VH)を複素データとして入力することもでき、研究レベルでは既に様々な技術検討がなされています。
学習データの準備
今回入力として用いるデータは、位相情報を保持しているレベル1.1のSLC(Single Look Complex: シングルルック複素画像)のデータを用意します。
衛星データの処理レベルについては、詳しくはこちらの記事をご覧ください。
識別対象は識別結果の分かりやすい橋を対象とします。そのため、途中でアノテーションも行います。
SARデータのダウンロード
まずは以下を実行してスカイツリー周辺のSARデータをダウンロードしていきます。
ここでダウンロードできるデータはCEOSと呼ばれるファイル形式をしています。
import os, requests
import geocoder
# Fields
BASE_API_URL = "https://file.tellusxdp.com/api/v1/origin/search/" # https://www.tellusxdp.com/docs/api-reference/palsar2-files-v1.html#/
ACCESS_TOKEN = "YOUR_TOKEN"
HEADERS = {"Authorization": "Bearer " + ACCESS_TOKEN}
TARGET_PLACE="Skytree, Tokyo"
SAVE_DIRECTORY="./data/"
# Functions
def rect_vs_point(ax, ay, aw, ah, bx, by):
return 1 if bx > ax and bx ay and by < ah else 0
def get_scene_list_slc(_get_params={}):
query = "palsar2-l11"
r = requests.get(BASE_API_URL + query, _get_params, headers=HEADERS)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
return r.json()
def get_slc_scenes(_target_json, _get_params={}):
# get file list
r = requests.get(_target_json["publish_link"], _get_params, headers=HEADERS)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
file_list = r.json()['files']
dataset_id = _target_json['dataset_id'] # folder name
# make dir
if os.path.exists(SAVE_DIRECTORY + dataset_id) == False:
os.makedirs(SAVE_DIRECTORY + dataset_id)
# downloading
print("[Start downloading]", dataset_id)
for _tmp in file_list:
r = requests.get(_tmp['url'], headers=HEADERS, stream=True)
if not r.status_code == requests.codes.ok:
r.raise_for_status()
with open(os.path.join(SAVE_DIRECTORY, dataset_id, _tmp['file_name']), "wb") as f:
f.write(r.content)
print(" - [Done]", _tmp['file_name'])
print("finished")
return
# Entry point
def main():
# extract slc list around the address
gc = geocoder.osm(TARGET_PLACE, timeout=5.0) # get latlon
slc_list_json = get_scene_list_slc({'after':'2019-1-01T00:00:00', 'polarisations':'HH+HV', 'page_size':'1000'}) # get single look complex list
target_places_json = [_ for _ in slc_list_json['items'] if rect_vs_point(_['bbox'][1], _['bbox'][0], _['bbox'][3], _['bbox'][2], gc.latlng[0], gc.latlng[1])] # lot_min, lat_min, lot_max...
target_ids = [_['dataset_id'] for _ in target_places_json]
print("[Matched SLCs]", target_ids)
for target_id in target_ids:
target_json = [_ for _ in slc_list_json['items'] if _['dataset_id'] == target_id][0]
# download the target file
get_slc_scenes(target_json)
break # if remove, download all data
if __name__=="__main__":
main()
実行すると、以下のようなログが表示され、全てのデータがダウンロードされます。今回は写りの良さから「ALOS2267472890-190507」のみを用いますので、他のデータをダウンロードしたくない場合は、適宜ソースコードを修正してください。
[Matched SLCs] ['ALOS2250690700-190113', 'ALOS2250912890-190115', 'ALOS2251130730-190116', 'ALOS2265402890-190423', 'ALOS2267250700-190505', 'ALOS2267472890-190507', 'ALOS2356482890-201229', 'ALOS2358112860-210109', 'ALOS2358552890-210112', 'ALOS2358770730-210113', 'ALOS2360182860-210123', 'ALOS2360622890-210126', 'ALOS2362252860-210206']シーン「ALOS2267472890-190507」は以下のようなSARデータです。

左下に見えるのが東京湾で、東京を中心としたSARデータであることが分かります。
これはCEOS(SLCのラッパ)→SLC(複素画像)→輝度値に変換して画像化していますが、現状ダウンロードされているデータは、ただのバイト列の並び(CEOS形式)でしかありません。
これから、このデータを使えるようにCEOSからSLCに変換していきます。また、画像化した際に8000×25000ピクセル程度の大きさがあり、処理を加えるには大きすぎるため、領域も限定していきます。
SARデータの画像化(CEOS→SLC→画像化)
ここでは手順のみを紹介します。詳細はこちらの記事(SAR画像の偏波を使った構造物推定(偏波の成分分解))をご覧ください。
以下のソースコードをslcinfo.pyで保存してください。これはSLCを格納するデータ構造(構造体)と考えて下さい。
import numpy as np
from tqdm import tqdm # !pip install tqdm
import struct
import copy as cp
class SLC_L11:
def __init__(self, _file_name):
self.file_name = _file_name
self.fp = 0
self.width = 0
self.height = 0
self.level = 0
self.format = ""
self.data = []
def get_width(self):
self.fp.seek(248)
self.width = int(self.fp.read(8))
print("width: ", self.width)
def get_height(self):
self.fp.seek(236)
self.height = int(self.fp.read(8))
print("height: ", self.height)
def get_level(self):
self.fp.seek(276) # if l1.1, return "544"
self.level = int(self.fp.read(4))
def get_format(self):
self.fp.seek(400)
self.format = self.fp.read(28).decode()
def get_data(self):
self.fp.seek(720)
prefix_byte = 544
data = np.zeros((self.height, self.width, 2))
width_byte_length = prefix_byte + self.width*8 # prefix + width * byte (i32bit + q32bit)
for i in tqdm(range(self.height)):
data_line = struct.unpack(">%s"%(int((width_byte_length)/4))+"f", self.fp.read(int(width_byte_length)))
data_line = np.asarray(data_line).reshape(1, -1)
data_line = data_line[:, int(prefix_byte/4):] # float_byte:
slc = data_line[:,::2] + 1j*data_line[:,1::2]
data[i, :, 0] = slc.real
data[i, :, 1] = slc.imag
# multiplex
self.data = data[:, :, 0] + 1j*data[:, :, 1]
print("done")
def crop_data(self, _offset_x, _offset_y, _size):
self.data = self.data[_offset_y:(_offset_y+_size), _offset_x:(_offset_x+_size)]
def extract_data_cog(self, _offset_x, _offset_y, _size):
return cp.deepcopy(self.data[(_offset_y-_size):(_offset_y+_size), (_offset_x-_size):(_offset_x+_size)])
def parse(self):
self.fp = open(self.file_name, mode='rb')
self.get_width()
self.get_height()
self.get_level()
self.get_format()
self.get_data()
self.fp.close()
self.fp = 0
次に処理部は以下です。slcinfo.pyと同じフォルダにプログラムファイルを配置してください。また、CEOSの保存先フォルダも指定を忘れないようにして下さい。
import os
import struct
import numpy as np
import glob
import pickle
import gc
from slcinfo import SLC_L11
# Fields
SAVE_DIRECTORY="YOUR_PATH"
# Entry point
def main():
product_list = os.listdir(SAVE_DIRECTORY)
for product_name in product_list:
slc_list = glob.glob(SAVE_DIRECTORY + product_name + "/IMG-*_D")
for slc_name in slc_list:
print(slc_name)
slc = SLC_L11(slc_name)
slc.parse()
slc.crop_data(1500, 15000, 5000) # if you use cropping
with open(slc_name + ".pkl", "wb") as f:
pickle.dump(slc, f)
slc = None
gc.collect()
if __name__=="__main__":
main()
実行すると、CEOS→SLCに変換し、CEOSの名前+.pklという拡張子で同フォルダに保存されます。なお、変換の際に領域を限定(画像切り抜き)しています。
SARデータの中には、偏波と呼ばれる観測条件の異なる4種類のデータが含まれています。詳細な説明は割愛しますが、今回は写りの良さからHV偏波のみ用いるため、他のVH、HH, VVらの変換は行わなくてもよいです。
次に、変換したSLCを画像として見たいと思います。画像化は以下のように行います。こちらも同様にslcinfo.pyと同じフォルダにプログラムファイルを配置してください。また、CEOSの保存先フォルダも指定を忘れないようにして下さい。
import os
import matplotlib as mpl
mpl.use('Agg')
import struct
import numpy as np
import glob
from tqdm import tqdm
import pickle
import cv2
import matplotlib.pyplot as plt
from slcinfo import SLC_L11
import gc
# Fields
SAVE_DIRECTORY="YOUR_PATH"
def get_intensity(_slc):
return 20*np.log10(abs(_slc)) - 83.0 - 32.0
def normalization(_x):
return (_x-np.amin(_x))/(np.amax(_x)-np.amin(_x))
def adjust_value(_x):
_x = np.asarray(normalization(_x)*255, dtype="uint8")
return cv2.equalizeHist(_x)
def slc2pauli(_hh, _hv, _vv, _vh, _cross=0):
if _cross == 0:
_cross = (_hv + _vh) / 2
else:
_cross = _hv
single = ((_hh+_vv)/np.sqrt(2)) # single, odd-bounce.
double = ((_hh-_vv)/np.sqrt(2)) # double, even-bounce
vol = np.sqrt(2)*_cross # vol
return np.asarray([single, double, vol])
def grayplot(_file_name, _v):
plt.figure()
#plt.imshow(_v, cmap = "gray")
#plt.savefig(filename)
plt.imsave(_file_name, _v, cmap = "gray")
print("[Save]", _file_name)
def rgbplot(_file_name, _alpha_r, _gamma_g, _beta_b):
plttot=(np.dstack([_alpha_r, _gamma_g, _beta_b]))
plttot=np.asarray(plttot, dtype="uint8")
plt.figure()
plt.imshow(plttot)
plt.imsave(_file_name, plttot)
print("[Save]", _file_name)
return
# Entry point
def main():
product_list = os.listdir(SAVE_DIRECTORY)
for product_name in product_list:
slc_list = glob.glob(SAVE_DIRECTORY + product_name + "/IMG-*.pkl")
for slc_name in slc_list:
with open(slc_name, "rb") as f:
slc = pickle.load(f)
if "IMG-HV" in slc_name:
slc_hv = slc.data
if "IMG-HH" in slc_name:
slc_hh = slc.data
if "IMG-VV" in slc_name:
slc_vv = slc.data
if "IMG-VH" in slc_name:
slc_vh = slc.data
slc_tmp = get_intensity(slc.data)
grayplot(slc_name + "_p.png", adjust_value(slc_tmp))
slc = None
gc.collect()
if __name__=="__main__":
main()
これを実行するとCEOSが保存されているフォルダに「CEOSの名前+_p.png」というファイルが書き出されていると思います。それがSLCを画像化した、いわゆるSAR画像と呼ばれるものです。次のようなファイルが最低限揃っていればよいです。

今回は元画像が大きいため、以下の領域を切り抜いています。画像の大きさは5000×
5000です。ここから、学習データを作っていきたいと思います。

今回は、このSAR画像(SLC)から橋を識別しようと思います。
学習データの生成
画像化したSLCを元にアノテーションを行っていきます。最終的に複素ニューラルネットワークに入力させる複素画像は矩形の領域とするため、橋の中心座標をアノテーションし、後にプログラムで矩形として切り抜いていきます。イメージ的には以下のようになります。

それでは、ペイントやGIMP等のソフトウェアを使い1つ1つ橋の中心座標を取得(アノテーション)していきます。皆様は大変だと思いますので用意したこちら(bridge_center.npy)をご利用下さい。
なお、今回アノテーションした領域は以下の通りです。クラスは2値分類で、その他データ(ノイズ)と橋データです。
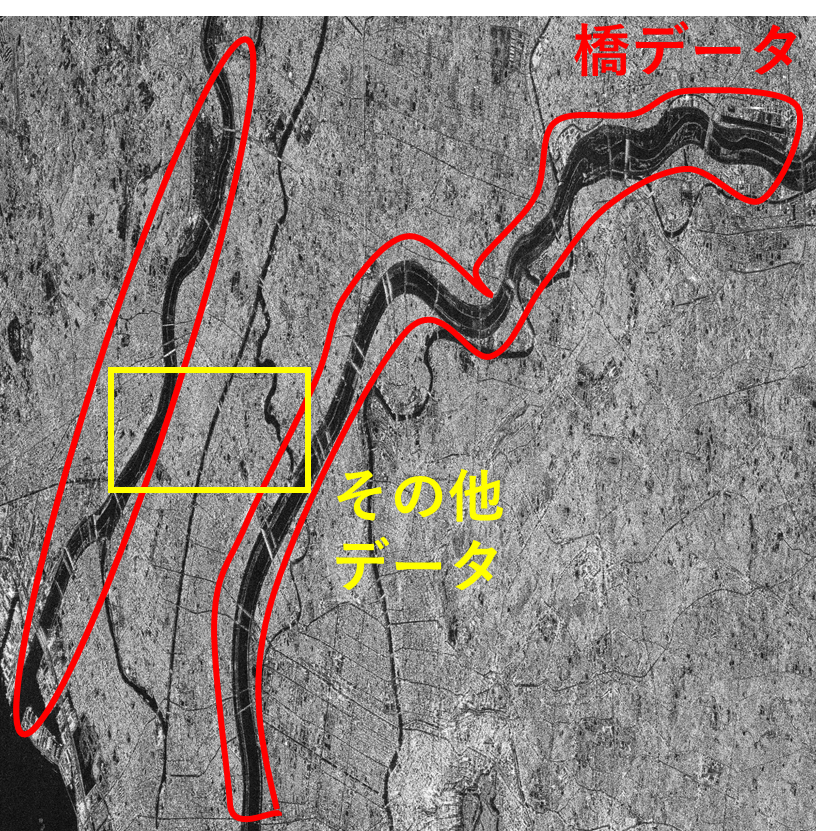
それではアノテーションファイルを元に学習データの生成及び水増しを行っていきたいと思います。以下のプログラムを実行してください。実行にあたって、上記で作成したpklファイル(SLCデータ)のパス、bridge_center.npyのパスを通すようにしてください。また、学習データの出力先フォルダも作ってください。今回は”./data/train/”及び”./data/test/”配下としています。
import os
import matplotlib as mpl
mpl.use('Agg')
import struct
import numpy as np
import glob
from tqdm import tqdm
import pickle
import cv2
import matplotlib.pyplot as plt
from slcinfo import SLC_L11
import gc
import random as rd
def get_intensity(_slc):
return 20*np.log10(abs(_slc)) - 83.0 - 32.0
def adjust_value(_x):
_x = np.asarray(normalization(_x)*255, dtype="uint8")
return cv2.equalizeHist(_x)
def grayplot(_file_name, _v):
plt.figure()
plt.imsave(_file_name, _v, cmap = "gray")
print("[Save]", _file_name)
def normalization(_x):
return (_x-np.amin(_x))/(np.amax(_x)-np.amin(_x))
bridge_center = np.load("./bridge_center.npy")
noise_data_cog_x = 1064
noise_data_cog_y = 1650
noise_data_range = 600
train_bc = bridge_center[:-3]
test_bc = bridge_center[-3:]
save_slc_path = "YOUR_PATH"
random_num = 5
image_size = 70
train_x_dataset = np.zeros(((random_num*train_bc.shape[0]*2), image_size, image_size, 2))
train_y_dataset = np.zeros(((random_num*train_bc.shape[0]*2), 2))
test_x_dataset = np.zeros(((test_bc.shape[0]*2), image_size, image_size, 2))
test_y_dataset = np.zeros(((test_bc.shape[0]*2), 2))
with open(save_slc_path, "rb") as f:
slc_data = pickle.load(f)
# train
data_counter = 0
for i in range(train_bc.shape[0]):
for j in range(random_num):
offset = rd.randint(-4, 4)
tmp_x = train_bc[i, 0] + offset
tmp_y = train_bc[i, 1] + offset
slc_tmp = slc_data.extract_data_cog(int(tmp_x), int(tmp_y), int(image_size/2))
train_x_dataset[data_counter, :, :, 0] = slc_tmp.real
train_x_dataset[data_counter, :, :, 1] = slc_tmp.imag
train_y_dataset[data_counter, 0] = 1
slc_tmp = get_intensity(slc_tmp)
grayplot("./data/train/" + str(data_counter) + "_v.png", adjust_value(slc_tmp))
data_counter += 1
for i in range(int(train_x_dataset.shape[0]*0.5)):
offset = rd.randint(-int(noise_data_range*0.5), int(noise_data_range*0.5))
tmp_x = noise_data_cog_x + offset
tmp_y = noise_data_cog_y + offset
slc_tmp = slc_data.extract_data_cog(int(tmp_x), int(tmp_y), int(image_size/2))
train_x_dataset[data_counter, :, :, 0] = slc_tmp.real
train_x_dataset[data_counter, :, :, 1] = slc_tmp.imag
train_y_dataset[data_counter, 1] = 1
slc_tmp = get_intensity(slc_tmp)
grayplot("./data/train/" + str(data_counter) + "_v.png", adjust_value(slc_tmp))
data_counter += 1
np.save("./data/train/train_x.npy", train_x_dataset)
np.save("./data/train/train_y.npy", train_y_dataset)
# test
data_counter = 0
for i in range(test_bc.shape[0]):
tmp_x = test_bc[i, 0]
tmp_y = test_bc[i, 1]
slc_tmp = slc_data.extract_data_cog(int(tmp_x), int(tmp_y), int(image_size/2))
test_x_dataset[data_counter, :, :, 0] = slc_tmp.real
test_x_dataset[data_counter, :, :, 1] = slc_tmp.imag
test_y_dataset[data_counter, 0] = 1
slc_tmp = get_intensity(slc_tmp)
grayplot("./data/test/" + str(data_counter) + "_v.png", adjust_value(slc_tmp))
data_counter += 1
for i in range(test_bc.shape[0]):
offset = rd.randint(-int(noise_data_range*0.5), int(noise_data_range*0.5))
tmp_x = noise_data_cog_x + offset
tmp_y = noise_data_cog_y + offset
slc_tmp = slc_data.extract_data_cog(int(tmp_x), int(tmp_y), int(image_size/2))
test_x_dataset[data_counter, :, :, 0] = slc_tmp.real
test_x_dataset[data_counter, :, :, 1] = slc_tmp.imag
test_y_dataset[data_counter, 1] = 1
slc_tmp = get_intensity(slc_tmp)
grayplot("./data/test/" + str(data_counter) + "_v.png", adjust_value(slc_tmp))
data_counter += 1
np.save("./data/test/test_x.npy", test_x_dataset)
np.save("./data/test/test_y.npy", test_y_dataset)
こちらを実行すると”data/train”と”data/test”フォルダに次のように学習画像が生成されています。以下が橋クラスの画像です。

以下がその他クラスの画像です。

これ等画像はあくまでも人間が理解するためのもので、実際の学習では用いません。実際に用いるのは複素画像をラッピングしたnpyファイルです。
ここまで終えられたら、最終的に次の学習及びテストデータがあるかと思われます。
“./data/train/train_x.npy”
“./data/train/train_y.npy”
“./data/test/test_x.npy”
“./data/test/test_x.npy”
こちらがありましたら、学習データの準備は終了です。最後に簡単にソースコードの説明をします。以下の部分が学習データ生成で最も重要な部分です。
for i in range(train_bc.shape[0]):
for j in range(random_num):
offset = rd.randint(-4, 4)
tmp_x = train_bc[i, 0] + offset
tmp_y = train_bc[i, 1] + offset
slc_tmp = slc_data.extract_data_cog(int(tmp_x), int(tmp_y), int(image_size/2))
train_x_dataset[data_counter, :, :, 0] = slc_tmp.real
train_x_dataset[data_counter, :, :, 1] = slc_tmp.imag
train_y_dataset[data_counter, 0] = 1
“train_bc”には橋の中心座標群が入っていますので、その各中心座標に多少のランダムノイズを複数回与えて、切り抜きを行っています。切り抜きはSLC(複素画像)から行っています。切り抜いた後は、SLC及びSLCの画像化を行い、複素画像及びSAR画像を保存しています。複素画像の保存は、slc_tmp.real、slc_tmp.imagと書かれているところです。こちらで複素成分を取り出して配列に保存しています。この配列は後に、train_xという名前で保存されています。
なお、テストデータは橋及びその他を学習データと被らないように3枚ずつ用意しています。今回はこの計6枚を間違えずに識別するというのが最終ゴールになります。

一目で見て、橋と分かるものもあれば、他の領域と区別がつかないものもありますね。果たして複素ニューラルネットワークを用いることでこれらが識別できるのでしょうか。
TensorflowとKerasを用いた複素ニューラルネットワークの構築
さて、いよいよ本題です。データセットの準備で少し間が空いてしまいましたが、複素数の理論を参考に複素ニューラルネットワークを構築していきたいと思います。今回は可読性の高いTensorflow+Kerasで実装していきます。
複素ニューラルネットワークの構成要素は以下の3つです。
・複素ニューラルネットワークの本体
こちらは複素数の計算方法を取り入れたニューラルネットワークを指しています。
・複素ニューラルネットワークの損失関数
複素ニューラルネットワークにおける分類は回転の角度によって示されるため、「クラス0は角度0~180度の間であれば正解」等を評価する損失関数が必要です
・ラベル↔クラス変換
一般的なクラスは0(橋クラス)、1(その他クラス)等のように別れていますが、複素ニューラルネットワークの出力と合わせるためには角度情報に変換する必要があります。
これから、この3つの実装を説明していきます。なお、最後に、これらをまとめたプログラムを提示するので、この項は目を通すだけでよいです。
複素ニューラルネットワークの本体
それでは理論で説明した以下の式を実装していきます。
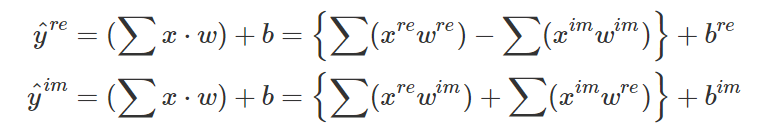
これをプログラムで実装すると以下のようになります。
class Cx2DAffine(Layer):
def __init__(self, output_dim, activation, **kwargs):
self.output_dim = output_dim
self.activation = activation
super(Cx2DAffine, self).__init__(**kwargs)
def build(self, input_shape):
# initialization
self.weight_real = self.add_weight(name='weight_real',
shape=(input_shape[2], self.output_dim),
initializer='glorot_uniform')
self.weight_imag = self.add_weight(name='weight_imag',
shape=(input_shape[2], self.output_dim),
initializer='glorot_uniform')
self.bias_real = self.add_weight(name='bias_real',
shape=(1, self.output_dim),
initializer='zeros')
self.bias_imag = self.add_weight(name='bias_imag',
shape=(1, self.output_dim),
initializer='zeros')
super(Cx2DAffine, self).build(input_shape)
def call(self, x):
# input
x_real = Lambda(lambda x: x[:, 0, :], output_shape=(x.shape[2], ))(x) # real
x_imag = Lambda(lambda x: x[:, 1, :], output_shape=(x.shape[2], ))(x) # imag
# computation according to mpx
real = K.dot(x_real, self.weight_real) - K.dot(x_imag, self.weight_imag)
imag = K.dot(x_real, self.weight_imag) + K.dot(x_imag, self.weight_real)
real = real + self.bias_real
imag = imag + self.bias_imag
# activation
if self.activation == 'normalize':
length = K.sqrt( K.pow(real, 2) + K.pow(imag, 2) )
real = real / length
imag = imag / length
# expand for concatenation
real = K.expand_dims(real, 1)
imag = K.expand_dims(imag, 1)
# merge mpx
cmpx = keras.layers.concatenate([real, imag], axis=1)
return cmpx
def compute_output_shape(self, input_shape):
return(input_shape[0], 2, self.output_dim)
こちらはKeras上でカスタムレイヤーとして定義しているため、KerasのConvやDense関数と同じように使うことができます(後述)。
数式の部分は以下のように実装されています。
real = K.dot(x_real, self.weight_real) - K.dot(x_imag, self.weight_imag)
imag = K.dot(x_real, self.weight_imag) + K.dot(x_imag, self.weight_real)また、正規化部分(活性化関数)は以下のように実装されています。
# activation
if self.activation == 'normalize':
length = K.sqrt( K.pow(real, 2) + K.pow(imag, 2) )
real = real / length
imag = imag / length複素ニューラルネットワークの損失関数
複素ニューラルネットワークでは角度によってクラス分類を行うため、それを評価する関数が必要です。また、重要なのは周期性です。次の画像の右側のように円の対角線上を同じクラスにすることが重要です。こちらも損失関数に取り入れる必要があります。
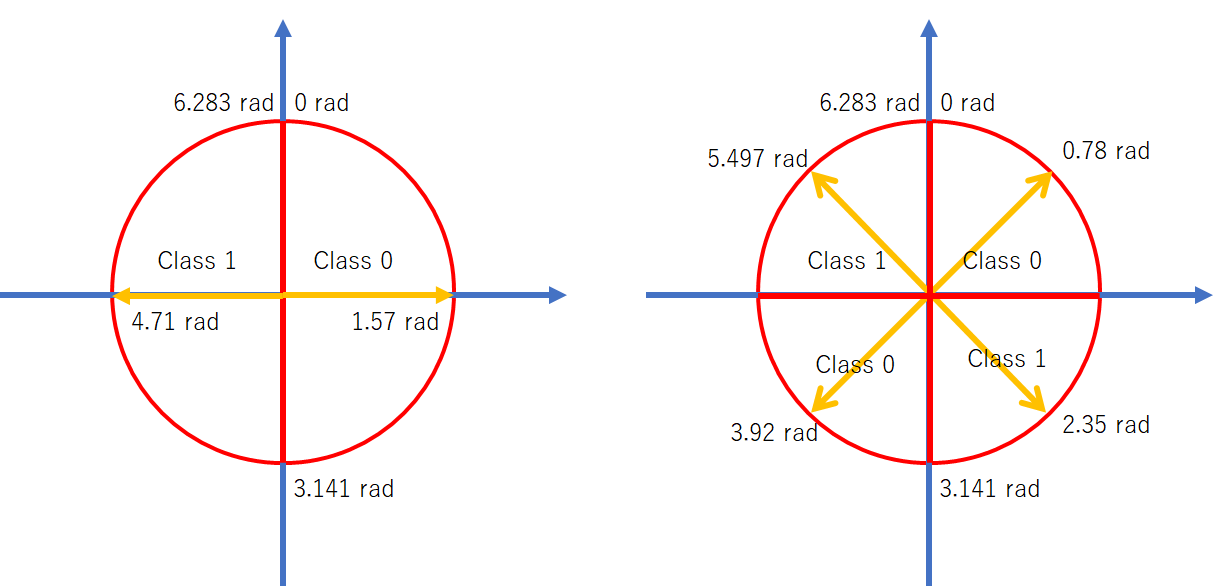
左は周期性を持たないクラス分類、右は周期性(p=2)を持つクラス分類(今回の実装)
これらを実装すると次のようなコードになります。
def loss_z(y, y_hat):
y_real = Lambda(lambda x: x[:, 0, :])(y) # real
y_imag = Lambda(lambda x: x[:, 1, :])(y) # imag
y_hat_real = Lambda(lambda x: x[:, 0, 0])(y_hat) # real
y_hat_imag = Lambda(lambda x: x[:, 1, 0])(y_hat) # imag
y_hat_real = K.expand_dims(y_hat_real, 1)
y_hat_imag = K.expand_dims(y_hat_imag, 1)
errors_real = y_real - y_hat_real
errors_imag = y_imag - y_hat_imag
errors = K.abs(errors_real) + K.abs(errors_imag)
return K.min(errors, axis=1)
最後のK.min関数が対角線上どちらかのクラスを示していれば正解といったロジックを担っています。
ラベル↔クラス変換
最後にクラスをラベルデータ(角度)に変換、もしくはその逆といった相互変換するプログラムを実装します。プログラムは以下のように非常に単純です。
def class_to_label(_class, _categories=2, _periodicity=2):
target_class = (_class + 0.5 + (_categories * np.arange(_periodicity))) / (_categories * _periodicity) * 2 * 3.14159265358979323846
target_class = np.exp(1j*target_class)
return_value = []
return_value = np.empty((2, _periodicity))
for i in range(_periodicity):
return_value[0, i] = target_class.real[i]
return_value[1, i] = target_class.imag[i]
return np.array(return_value, dtype='float32')
def label_to_class(_estimate, _categories=2, _periodicity=2):
angle = np.mod(np.angle(_estimate) + 2*np.pi, 2*np.pi)
p = int(np.floor (_categories * _periodicity * angle / (2*np.pi)))
return np.mod(p, _categories)
class_to_label関数はクラス、最大のクラス数、周期性を与えると、単位円上の座標(複素数)が返ってくるプログラムです。象限の真ん中にクラスが来るよう+0.5されています。
label_to_class関数は複素数、最大のクラス数、周期性を与えると、クラス番号が返ってくる仕組みです。周期性を上手く利用するため、最後にモジュラー演算が入っています。
これにて必要なプログラム(道具)が全て揃いました、次の項で統合させて実際に動作させてみましょう。
複素ニューラルネットワークで学習
では、これまでに準備してきた、データセット及び複素ニューラルネットワークを用いて実際に学習を行っていきます。
データセット読み込みや構築した複素ニューラルネットワークを全部取り入れたプログラムは以下になります。プログラムファイルは好きな名前で保存してよいです。
import os
import matplotlib as mpl
mpl.use('Agg')
import struct
import numpy as np
import glob
from tqdm import tqdm
import pickle
import cv2
import matplotlib.pyplot as plt
import gc
import random as rd
# keras
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras import backend as K
from tensorflow.keras import Input
from tensorflow.keras.layers import (Layer, InputLayer, Conv2D, Lambda)
from tensorflow.keras.models import Model
from tensorflow import keras
# custom class
class Cx2DAffine(Layer):
def __init__(self, output_dim, activation, **kwargs):
self.output_dim = output_dim
self.activation = activation
super(Cx2DAffine, self).__init__(**kwargs)
def build(self, input_shape):
# initialization
self.weight_real = self.add_weight(name='weight_real',
shape=(input_shape[2], self.output_dim),
initializer='glorot_uniform')
self.weight_imag = self.add_weight(name='weight_imag',
shape=(input_shape[2], self.output_dim),
initializer='glorot_uniform')
self.bias_real = self.add_weight(name='bias_real',
shape=(1, self.output_dim),
initializer='zeros')
self.bias_imag = self.add_weight(name='bias_imag',
shape=(1, self.output_dim),
initializer='zeros')
super(Cx2DAffine, self).build(input_shape)
def call(self, x):
# input
x_real = Lambda(lambda x: x[:, 0, :], output_shape=(x.shape[2], ))(x) # real
x_imag = Lambda(lambda x: x[:, 1, :], output_shape=(x.shape[2], ))(x) # imag
# computation according to mpx
real = K.dot(x_real, self.weight_real) - K.dot(x_imag, self.weight_imag)
imag = K.dot(x_real, self.weight_imag) + K.dot(x_imag, self.weight_real)
real = real + self.bias_real
imag = imag + self.bias_imag
# activation
if self.activation == 'normalize':
length = K.sqrt( K.pow(real, 2) + K.pow(imag, 2) )
real = real / length
imag = imag / length
# expand for concatenation
real = K.expand_dims(real, 1)
imag = K.expand_dims(imag, 1)
# merge mpx
cmpx = keras.layers.concatenate([real, imag], axis=1)
return cmpx
def compute_output_shape(self, input_shape):
return(input_shape[0], 2, self.output_dim)
def loss_z(y, y_hat):
y_real = Lambda(lambda x: x[:, 0, :])(y) # real
y_imag = Lambda(lambda x: x[:, 1, :])(y) # imag
y_hat_real = Lambda(lambda x: x[:, 0, 0])(y_hat) # real
y_hat_imag = Lambda(lambda x: x[:, 1, 0])(y_hat) # imag
y_hat_real = K.expand_dims(y_hat_real, 1)
y_hat_imag = K.expand_dims(y_hat_imag, 1)
errors_real = y_real - y_hat_real
errors_imag = y_imag - y_hat_imag
errors = K.abs(errors_real) + K.abs(errors_imag)
return K.min(errors, axis=1)
def class_to_label(_class, _categories=2, _periodicity=2):
target_class = (_class + 0.5 + (_categories * np.arange(_periodicity))) / (_categories * _periodicity) * 2 * 3.14159265358979323846
target_class = np.exp(1j*target_class)
return_value = []
return_value = np.empty((2, _periodicity))
for i in range(_periodicity):
return_value[0, i] = target_class.real[i]
return_value[1, i] = target_class.imag[i]
return np.array(return_value, dtype='float32')
def label_to_class(_estimate, _categories=2, _periodicity=2):
angle = np.mod(np.angle(_estimate) + 2*np.pi, 2*np.pi)
p = int(np.floor (_categories * _periodicity * angle / (2*np.pi)))
return np.mod(p, _categories)
def main():
# preparing dataset
train_x_dataset = np.load("./data/train/train_x.npy")
train_y_dataset = np.load("./data/train/train_y.npy")
test_x_dataset = np.load("./data/test/test_x.npy")
test_y_dataset = np.load("./data/test/test_y.npy")
train_x_dataset = train_x_dataset.reshape((train_x_dataset.shape[0], -1, 2))
train_x_dataset = np.transpose(train_x_dataset, (0, 2, 1))
train_y_dataset = np.argmax(train_y_dataset, axis=1)
periodicity = 2
label_data = np.empty((0, 2, periodicity))
for i in range(train_y_dataset.shape[0]):
label_data = np.append(label_data, [class_to_label(train_y_dataset[i])], axis=0)
train_y_dataset = label_data
test_x_dataset = test_x_dataset.reshape((test_x_dataset.shape[0], -1, 2))
test_x_dataset = np.transpose(test_x_dataset, (0, 2, 1))
test_y_dataset = np.argmax(test_y_dataset, axis=1)
# build architecture
input = Input(shape=(2, 70*70,))
cxnn = Cx2DAffine(128, activation='normalize')(input)
cxnn = Cx2DAffine(128, activation='normalize')(cxnn)
cxnn = Cx2DAffine(128, activation='normalize')(cxnn)
cxnn = Cx2DAffine(1, activation='normalize')(cxnn)
cxnn_model = Model(input, cxnn)
cxnn_model.compile(optimizer='adam', loss=loss_z)
print(cxnn_model.summary())
# train
cxnn_model.fit(train_x_dataset, train_y_dataset, epochs=1000, batch_size=5, shuffle=True)
# prediction
result = cxnn_model.predict(test_x_dataset)
for i, _tmp in enumerate(result):
mlx = _tmp[0] + 1j*_tmp[1]
print("prediction:", label_to_class(mlx))
print("class:", test_y_dataset[i])
print("---------")
if __name__=="__main__":
main()
このまま本プログラムを実行すると次のようにネットワーク構造が表示されて学習が始まるかと思います。
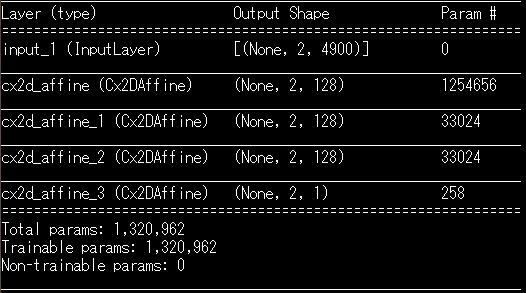
今回は軽量なモデル構造にしています。ニューラルネットワークでいうところのDense4層と同じです。ネットワーク構造を変更する場合には以下を変更しましょう。Cx2DAffineと書かれているものが先ほど作成した複素ニューラルネットワークです。KerasのConvやDense関数と同じように使うことが出来ます。
# build architecture
input = Input(shape=(2, 70*70,))
cxnn = Cx2DAffine(128, activation='normalize')(input)
cxnn = Cx2DAffine(128, activation='normalize')(cxnn)
cxnn = Cx2DAffine(128, activation='normalize')(cxnn)
cxnn = Cx2DAffine(1, activation='normalize')(cxnn)
cxnn_model = Model(input, cxnn)
cxnn_model.compile(optimizer='adam', loss=loss_z)
print(cxnn_model.summary())GPU等でエラーが生じず、学習が無事に終了すると以下のような画面が表示されます。
学習を終えると自動でテストデータを識別します。今回の表示されている内容だと、クラス0(橋)、クラス1(その他)を間違いなく分類していることが確認できました。学習時間やネットワーク構造によって結果は変化しますので、皆さまもどのような構造だと精度が出るか実験して見てください。
ここまでで、SLC(複素データ)を入力データとして複素ニューラルネットワークに解析されるといった目的が達成されました。
複素ニューラルネットワークの結果
それでは最後に、学習した結果の詳細を見ていきます。まず橋クラスは以下のような結果です。
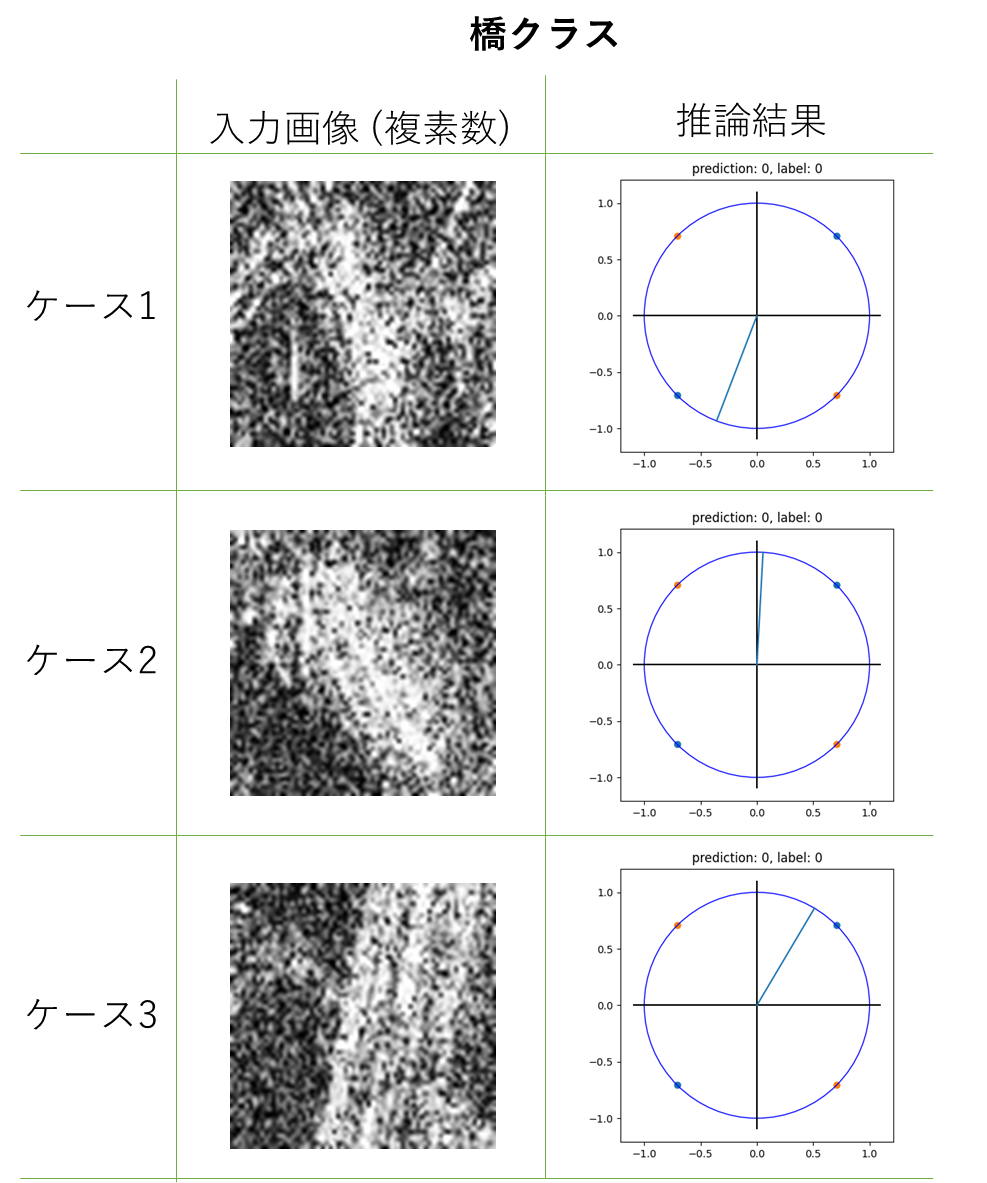
推論結果の単位円は青色が0クラス(橋)、橙色が1クラス(その他)を示しています。このため、この画像では全て青(橋)を示していればよいということになります。入力画像は画像化されていますが、実際は複素データ(SLC)です。
ケース2がギリギリ青色の空間にいます。このため、ケース2はその他クラスと見分けがつきにくいということになります。また、ケース1及びケース3では各々、対角線上の同じクラスを示しています。このことから、構築した損失関数が上手く働いているということが分かります。たまに過学習を起こすと同じ象限のクラスばかりを指すようになってしまいます。
次に、その他クラスの結果は以下の通りです。
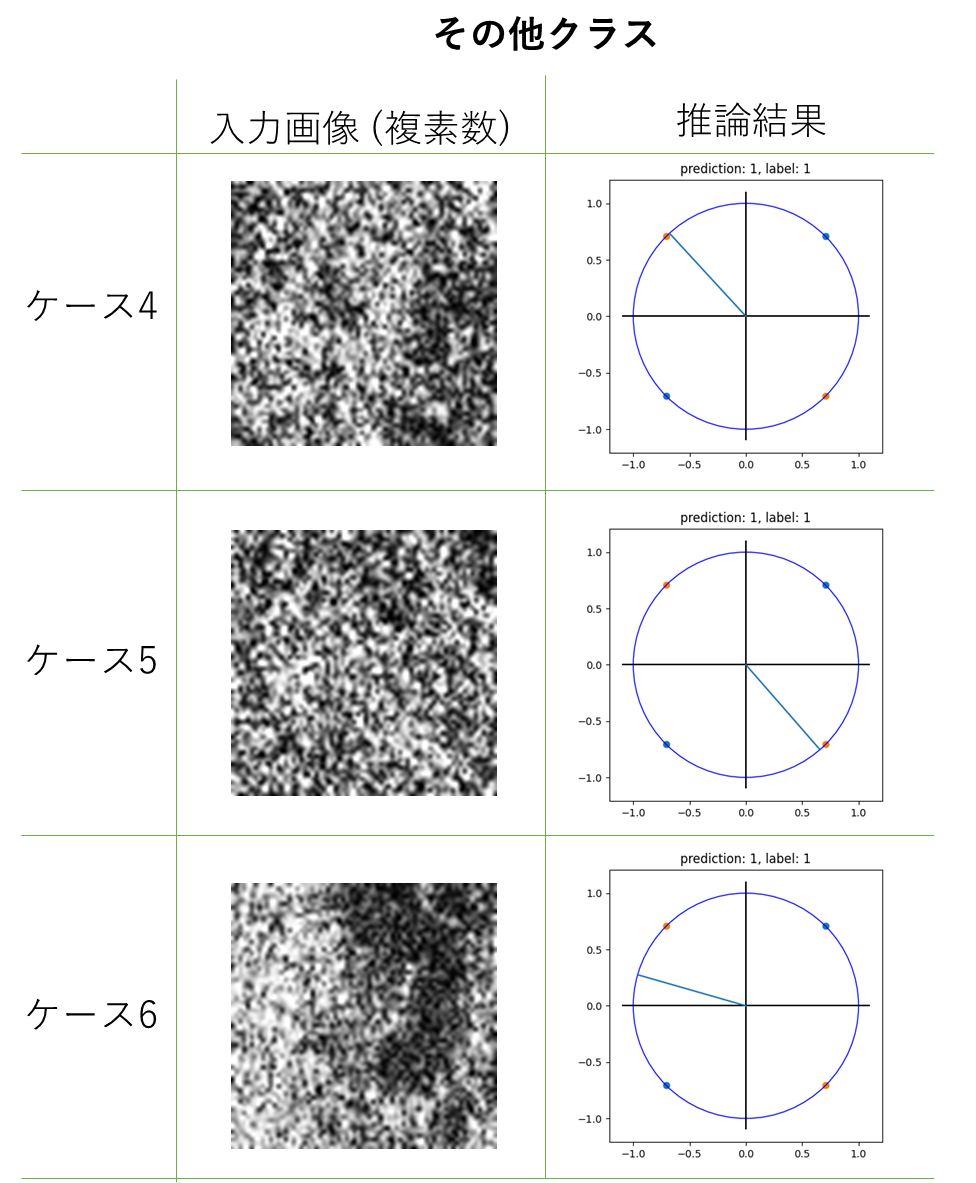
こちらは迷いも見られず、橙色(その他クラス)を指しています。このため、その他クラスは橋と見間違うことはないが、橋クラスはその他クラスと見間違うものがあったということが分かります。特にケース4及びケース5はその他クラスの象限の真ん中に位置するため、かなり高い確率で橋ではないということが分かったと考えられます。ケース6は川が少し写っているため、橋である可能性を疑ったため、象限の真ん中から少しズレたのではないかと考えられます。
まとめ
本稿ではSARデータ解析に特化した複素ニューラルネットワークを実装し、実際に物体識別するまでを行ってきました。世の中の多くのサービスがSAR画像を用いている中、SARデータ(SLC)をそのまま解析するというのは新鮮だったのではないでしょうか。性能においても、簡単な識別問題で評価を行いましたが、橋クラスとその他クラスを選り分けることができました。
今回は複素ニューラルネットワークの導入ということで、簡単なネットワークを構築して学習を行いましたが、これをベースに他の活性化関数を取り入れてみたり、他の関数と組み合わせてみたりして、よりディープで複雑な複素ニューラルネットワークの世界に足を運んでみてはいかがでしょうか。まだまだ未開拓な分野なので、何か新たな発見があるかもしれません。
本記事に出てくるコードはgithubでも公開しています。
https://github.com/sorabatake/article_18837_CxNN


