衛星データでここまでできる! ヤッホーが綺麗に返ってくる場所(やまびこスポット)の解析とシミュレーション
8月11日の山の日にちなんで、衛星データを活用してやまびこスポットが分かるのかのシミュレーションにチャレンジ。やまびこの文化や歴史と合わせてお楽しみください。
皆さんは山登りをした際に、綺麗な山が一望できる場所で「ヤッホー」と叫んだことがありますか?
その時に山から「ヤッホー」と叫んだ声が返ってくる現象を”やまびこ”といいます。
ただ、もしかしたらやまびこが返ってこなくて残念な気持ちになった方もいらっしゃるかもしれません。
本記事はやまびこについて、どのような場所であれば聞こえるのかを衛星データをはじめとしたリモートセンシングの知識を活用にすることで調査していく内容になっています。
本記事は8月11日の山の日に合わせて企画した、やまびこの名所を探る企画の1本目となります。2本目からは株式会社ヤマップ様にご協力いただいたやまびこスポットについて、机上での検証も行います。今後、素晴らしいやまびこスポットが見つかった際には宙畑編集部で現地を訪れやまびこの検証も行う予定です。
※現在、登山アプリ「YAMAP」では「山の日ヤッホー選手権2025」が開催されています。最優秀賞の方にはヤッホーブルーイングの「山の上のニューイとよなよなエールの12本アソート」がもらえるとのこと。ぜひご参加ください!
最後には、上記のような衛星データを活用することでやまびこのシミュレーターを実装します。
やまびことは?
やまびこは、山や谷などの地形によって音波が反射し、発声者のもとに遅れて戻ってくる現象です。「エコー(echo)」とも呼ばれますが、日本語の「やまびこ」は古来より親しまれてきた言葉であり、単に音の反射現象を示すだけでなく、山岳信仰や文学・音楽にも深く結び付いた文化的概念でもあります。
以下は、さらなるやまびこの理解のため、その定義を物理的側面と歴史的側面に分けて紹介します。
なお本連載は技術的なお話も多く出てきます。SARを学ぶ連載【SARデータ解析者への道】でおなじみのこめじゃらし君と楽しく学んでいきましょう。
まずは、やまびこの物理的な定義とメカニズムについて紹介します。やまびこは、主に以下の3点を考慮することで再現が可能です。
1.音波の反射
音波(声)は空気中を伝搬し、大気の密度や弾性が大きく異なる境界面に到達すると一部が反射します。山岳地形は 急斜面や断崖などの凹凸が大きいため、音波を効率良く反射させる「巨大な反射板」として機能します。2.遅延時間と距離の関係
空気中の音速は気温 15 ℃で約 340 m/s です。発声からやまびこが聞こえるまでの遅延時間が 2 秒であれば、音は往復で約 680 m を移動した計算になり、単純に計算をすると、反射面までの距離は約 340 m となります。この関係を利用すると、山肌までのおおよその距離を推定できます。3.音の減衰
伝搬する過程で音波は空気抵抗により減衰し、反射回数が多いほど聞こえにくくなります。そのため鮮明なやまびこを得るには、音源と反射面が一対一で向き合い、かつ吸音要素が少ない環境(音源反射する場所がコンクリートや岩など)が望ましいとされています。
やまびこは、物理的には音波の反射と遅延というシンプルな構造を持つ一方で、地形・植生・気象など多様な要素が絡み合う複合的現象でもあります。

次に、やまびこの歴史や文化について紹介します。

やまびこは古典文学や山岳信仰など、調べれば調べるほど奥深い世界だと分かります。
・古典文学への登場
『万葉集』や『古今和歌集』には、山中で声を発し“こだま”が返る様子を詠んだ歌が散見されます。こだまは、幽玄(奥深くて、はかり知れないこと)の象徴となり、しばしば孤独や無常観の比喩として描かれていました。例えば大伴宿禰家持が詠んだ「山彦の相とよむまで妻恋に鹿鳴く山辺に独りのみして(やまびこが響きあうほど鹿が妻を呼ぶ鳴き声が聞こえる山辺に、私は一人でいます)」があります。
・山岳信仰との関係
修験道では、山を神格化する考え方が根付きました。谷から返る声は山の神や精霊が応答したものとされ、やまびこは霊魔をはらう験(しるし)とも解釈されてきたそうです。今もなお山開きや祭礼で唱和を行う地域が残っています。多くは山の神やその眷属の性格を持つ、妖怪として’やまびこ’が登場しています。・音楽と芸能
能楽や民謡には、山彦を題材にした曲節が江戸時代には既に存在します。特に尺八や篠笛は、谷に響く残響を取り込みながら演奏することで、自然との共鳴を芸術に昇華させてきました。このように’やまびこ’は聴覚的な美を追求する文化装置でもあったのです。

余談ですが、すでにやまびこは物理的な条件で再現できるとその可能性を挙げたように、やまびこは科学教育に利用される側面や、観光資源として注目されるといった側面もあります。
例えば、「音の景観(soundscape)」という言葉をご存知ですか?やまびこは自然が生み出す伝統的な音の景観の一つであり、以下のような利点があります。
・観光資源としての価値
地域によっては、やまびこの場所を探索、体験ができるガイドツアーが企画され、地域経済の活性化に寄与したという事例もあるようです。また、山によってはやまびこポイントに看板を設置して、観光名所の一つとしてアピールしている場所もあるようです。・教育・科学コミュニケーション
中学校の理科分野では、音の伝搬速度や反射の授業で実験例として取り上げられています。現地のフィールドワークと、地学・物理学双方にまたがる学習効果が期待できます。また、自然を介すことで人の温かみも感じられるでしょう。
このように、やまびこは単なる自然現象にとどまらず、古来より人々の信仰や芸術に深く根付いてきたほか、今後も残る貴重な自然資源のひとつでしょう。

やまびこができる条件は?
では、やまびこができる条件について、もう少し踏み込んで考えてみましょう。やまびこの物理的な特性からある程度のやまびこが聞こえる条件は推定できそうです。
まずは、地形的な条件についてです。音波が発されてから反射して音源まで返ってくるためには、音源の周囲が何かに囲まれている地形であることが求められます。それらの条件を整理していくと、そのような地形は表1の形状だと推察できます。

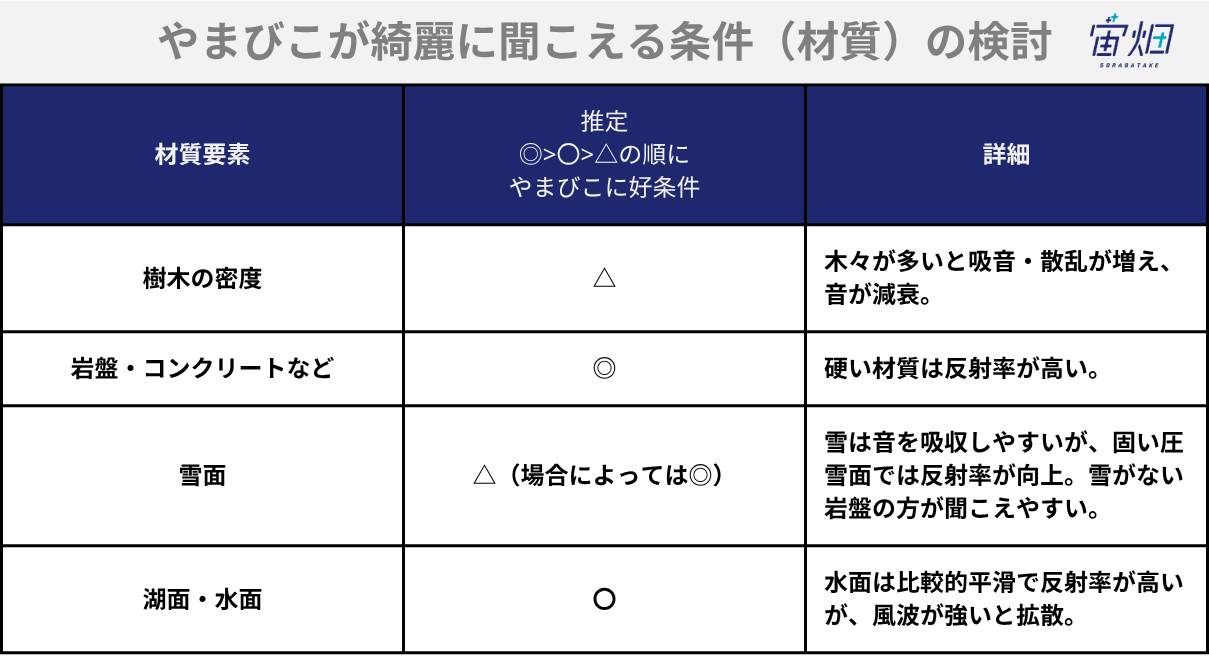
次に、音波が反射しやすい材質についてです。音波は硬く表面が滑らかな物質の方が反射しやすいです。音を吸収しやすいような素材では、音が減衰して音源まで返ってこないことが発生してしまいます。実際の山岳地帯で想定される物質では、表2のような条件だと推察ができます。
最後は、音波についてです。音波の音速が正しく計算されないと距離が正しくても聞こえてくるタイミングも変わります。
そこで重要なのは、音速は変化するということです。
リモートセンシングで多く用いられる電磁波(光)は速度が一定です。その普遍性を使用して、測量や位置が決定されることが基本になっています。
しかしながら、音は空気の中の振動なので、空気の様子が変化すると音の伝わるスピードも変化してしまいます。ここでの空気の変化とは、気温や湿度、気圧などの状態のことです。
例えば、気圧が高まると、空気の中の原子の粒が密集していて、沢山ぶつかり合うことで渋滞のようになるために遅くなります。厳密には、熱力学的な定義とその状態方程式によって決定しますが詳しくは割愛します。
音速が変化するイメージを持っていただくため、音速が気圧や気温によってどのような分布になるか、3Dでプロットした結果が図4です。
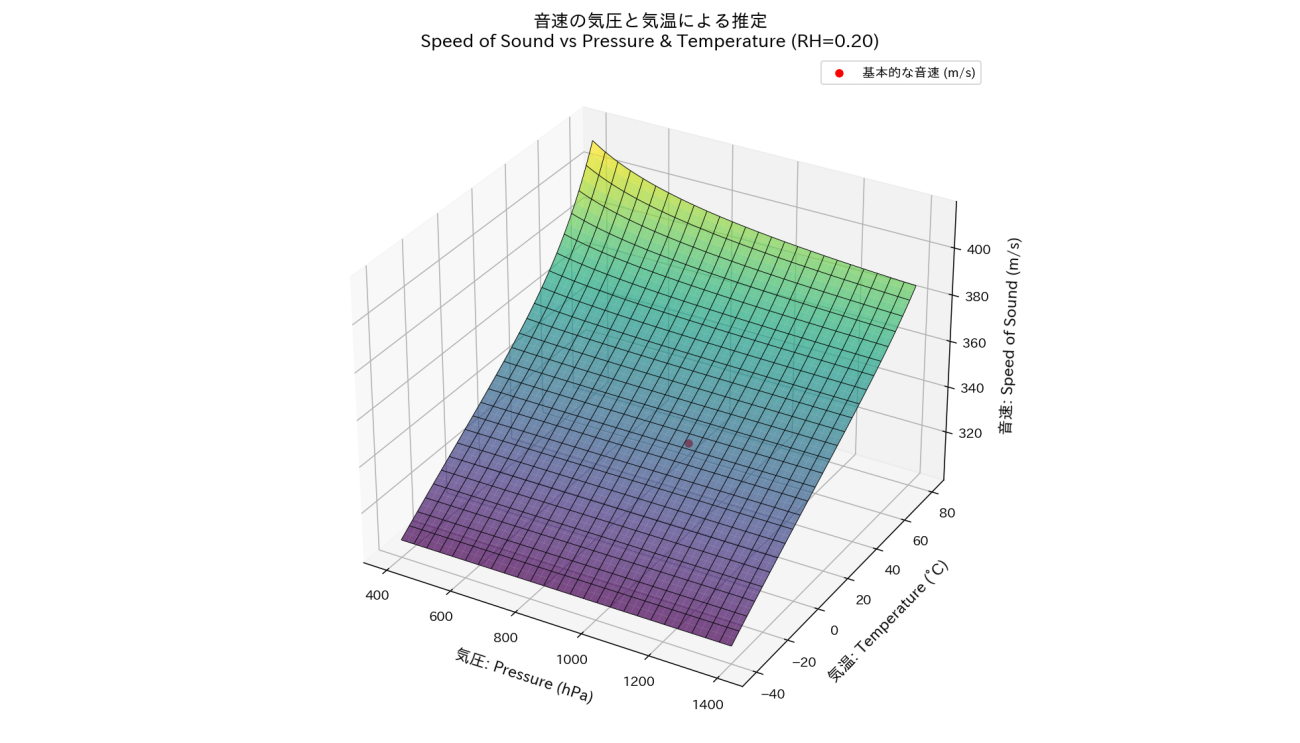
今回は、登山日和の乾燥した気候を想定して湿度20%で3D可視化しています。 図4から多くは気温によって音速は変化していて、秒速320mから秒速380mを推移しています。温度についても日本アルプスのような標高が高い場所では真夏でも気温が低いために15℃くらいを考えると秒速340mです(図 4の赤い点)。
以下、図4を可視化するためのPythonのコードです。
# --- 定数 ---
R_d = 287.05 # J/(kg*K) 乾燥空気
R_v = 461.5 # J/(kg*K) 水蒸気
cp_d = 1005.0 # J/(kg*K)
cp_v = 1850.0 # J/(kg*K) 近似
def speed_of_sound_dry_air(T_K, gamma=1.4):
"""乾燥空気(理想気体)音速 [m/s]。T_K: Kelvin。"""
return np.sqrt(gamma * R_d * T_K)
def saturation_vapor_pressure_hPa(T_C):
"""Tetens式による飽和水蒸気圧 [hPa]; -40~+50℃程度で有効な近似。"""
return 6.112 * np.exp((17.67 * T_C) / (T_C + 243.5))
def specific_humidity(P_hPa, T_C, RH=0.5):
"""比湿 q [kg/kg] を気圧[hPa], 気温[°C], 相対湿度RH[0-1]から推定。"""
e_s = saturation_vapor_pressure_hPa(T_C) # hPa
e = RH * e_s
eps = R_d / R_v # ~0.622
w = eps * e / (P_hPa - e) # mixing ratio
q = w / (1 + w)
return q
def speed_of_sound_moist_air(P_hPa, T_C, RH=0.5):
"""湿り空気音速 [m/s](仮想温度 & 混合気体比熱近似)。"""
q = specific_humidity(P_hPa, T_C, RH=RH)
T_K = T_C + 273.15
# 仮想温度 (簡易)
T_v = T_K * (1.0 + 0.61 * q)
# 混合気体の cp, R, gamma
cp_mix = cp_d * (1 - q) + cp_v * q
R_mix = R_d * (1 - q) + R_v * q
cv_mix = cp_mix - R_mix
gamma_mix = cp_mix / cv_mix
return np.sqrt(gamma_mix * R_mix * T_v)
# ---- 計算グリッド ----
pressure_range_hPa = np.linspace(400, 1400, 200) # 地表付近の気圧範囲に変更(必要なら調整)
temperature_range_C = np.linspace(-40, 80, 200)
P_grid, T_grid = np.meshgrid(pressure_range_hPa, temperature_range_C)
# RH 設定(0=乾燥, 1=飽和)
RH_demo = 0.2
c_grid = speed_of_sound_moist_air(P_grid, T_grid, RH=RH_demo)
# 乾燥モデル(気圧非依存)も計算(比較用)
c_grid_dry = speed_of_sound_dry_air(T_grid + 273.15)
# 代表条件
P0_hPa = 1013.25
T0_C = 15.0
c0_dry = speed_of_sound_dry_air(T0_C + 273.15)
c0_moist = speed_of_sound_moist_air(P0_hPa, T0_C, RH=RH_demo)
print(f"Example dry : P={P0_hPa:.2f} hPa, T={T0_C:.1f} °C -> c={c0_dry:.2f} m/s")
print(f"Example moist : P={P0_hPa:.2f} hPa, T={T0_C:.1f} °C, RH={RH_demo:.2f} -> c={c0_moist:.2f} m/s")
# ---- 3D プロット ----
fig = plt.figure(figsize=(14, 8), dpi=140, facecolor="w", edgecolor="k")
ax = fig.add_subplot(111, projection='3d')
# Note: カラー指定しない(指示に従う)
ax.plot_surface(P_grid, T_grid, c_grid, linewidth=0, antialiased=True, alpha=0.7,
cmap='viridis',
# label="Sound Speed (m/s)",
label='_nolegend_'
)
ax.plot_wireframe(P_grid, T_grid, c_grid, rstride=8, cstride=8, linewidth=0.5,
color='k', ) # ワイヤーフレーム
ax.scatter(P0_hPa, T0_C, c0_moist, s=30, c='r',
label="基本的な音速 (m/s)") # 代表点
ax.set_xlabel('気圧: Pressure (hPa)', fontsize=12, labelpad=8)
ax.set_ylabel('気温: Temperature (°C)', fontsize=12, labelpad=8)
ax.set_zlabel('音速: Speed of Sound (m/s)', fontsize=12, labelpad=8)
ax.set_title(f'音速の気圧と気温による推定\nSpeed of Sound vs Pressure & Temperature (RH={RH_demo:.2f})', fontsize=14)
ax.legend()
ax.view_init(elev=30, azim=-60) # 視点調
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'speed_of_sound_3d.png'),)
plt.show()また、音量は遠くなればなるほど小さくなります。
では、現実的にはどれくらいまでの距離であれば聞こえるのかを確認していきます。音速と同様に大気の状態によって音波の吸収量が異なります。
Calculation of the Absorption of Sound by the Atmosphere: ISO 9613‑1 (1993)を参考にして、気温15℃の状態で相対湿度とやまびこの周波数によってどれくらい変化するのかを3Dプロットした結果が図5です。ちなみに、男性と女性によって発する声の高さが異なっていて、概ね男性は 100〜500hz、女性は200〜1000hzの声を発します。
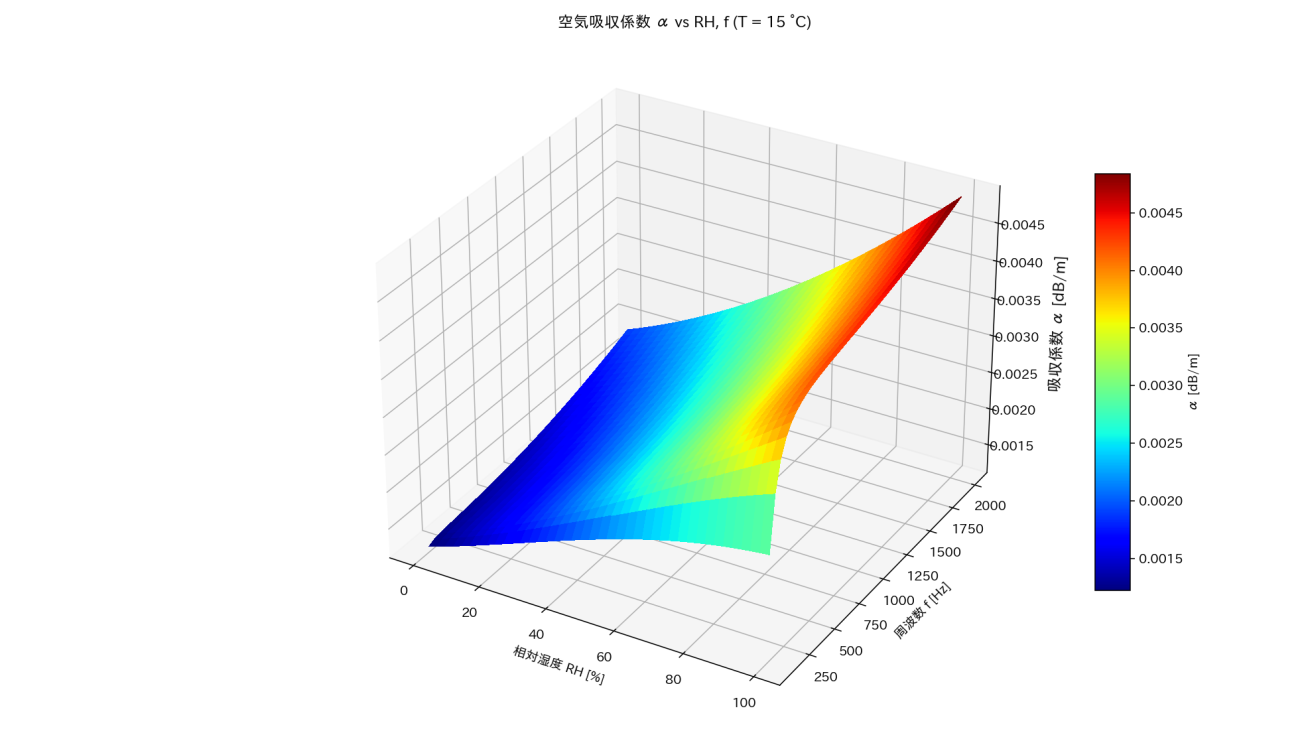
図5のように湿度が高いほど、声は吸収されやすく、発する声の周波数が高いほど、吸収されやすくなります。特に、湿度の変化には大きく影響されます。湿度が20%では 0.002前後の係数になります。この係数は声が1m進むごとに声の大きさがどの程度小さくなるかの係数です。
# --- alpha_iso9613 関数を再掲 ---
def saturation_pressure_pa(T_c):
return 610.78 * 10 ** (7.5 * T_c / (T_c + 237.3))
def alpha_iso9613(f_hz, T_c, RH, p_pa=101325):
T0 = 293.15
pr = 101325.0
T = T_c + 273.15
f = f_hz
Psat = 610.78 * 10 ** (7.5 * T_c / (T_c + 237.3))
h = RH / 100 * Psat / p_pa
FrO = (p_pa / pr) * (24 + 4.04e4 * h * (0.02 + h) / (0.391 + h))
FrN = (p_pa / pr) * (T / T0) ** (-0.5) * (9 + 280 * h * np.exp(-4.17 * ((T / T0) ** (-1/3) - 1)))
term1 = 1.84e-11 * (pr / p_pa) * np.sqrt(T / T0)
term2 = (T / T0) ** (-2.5) * (
0.01275 * np.exp(-2239.1 / T) / (FrO + (f ** 2) / FrO)
+ 0.1068 * np.exp(-3352.0 / T) / (FrN + (f ** 2) / FrN)
)
alpha = 8.686 * f ** 2 * (term1 + term2)
return alpha
T_c_fixed = 15.0 # 15 ℃ の断面で可視化
RH_range = np.linspace(0, 100, 40) # 湿度 [%]
f_range = np.linspace(100, 2000, 40) # 周波数 [Hz]
RH_mesh, f_mesh = np.meshgrid(RH_range, f_range)
alpha_mesh = alpha_iso9613(f_mesh, T_c_fixed, RH_mesh)
# 3D surface plot
fig = plt.figure(figsize=(14, 8), dpi=140, facecolor="w", edgecolor="k")
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(RH_mesh, f_mesh, alpha_mesh,
cmap=cm.jet, linewidth=0, antialiased=False)
ax.set_xlabel('相対湿度 RH [%]')
ax.set_ylabel('周波数 f [Hz]')
ax.set_zlabel('吸収係数 α [dB/m]', fontsize=12, labelpad=10)
ax.set_title(f'空気吸収係数 α vs RH, f (T = {T_c_fixed:.0f} °C)')
fig.colorbar(surf, shrink=0.6, aspect=12, label='α [dB/m]')
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'air_absorption_3d_fixed.png'))
plt.show()# 例: 15 ℃, RH 20 %, 400 Hz
T_c = 15.0
RH = 20.0
f = 400.0 # Hz 理由は、男性で約100~500Hz、女性で約200~1000Hz程度
alpha_db_per_m = alpha_iso9613(f, T_c, RH)
alpha_db_per_km = alpha_db_per_m * 1000
print(f"気温 {T_c:.0f} ℃, RH {RH:.0f} %, 周波数 {f/1000:.1f} kHz")
print(f"空気吸収係数 α ≈ {alpha_db_per_m:.4f} dB/m")
print(f" ≈ {alpha_db_per_km:.2f} dB/km")気温 15 ℃, RH 20 %, 周波数 0.4 kHz
空気吸収係数 α ≈ 0.0017 dB/m
≈ 1.67 dB/km
もう少し具体的な数値を用いることで現実的な理解に繋げていきましょう。
一般男性が大きな声を出せる音量は90dBほどです。このエネルギーが球体のように周囲に広がるごとに分散されるために、音量も小さくなっています。また、それに加えて図5の音波の吸収係数が加わる分だけ音が小さくなります。では、何メートルほど進むと、どの程度音量が小さくなるかを推定してみます。
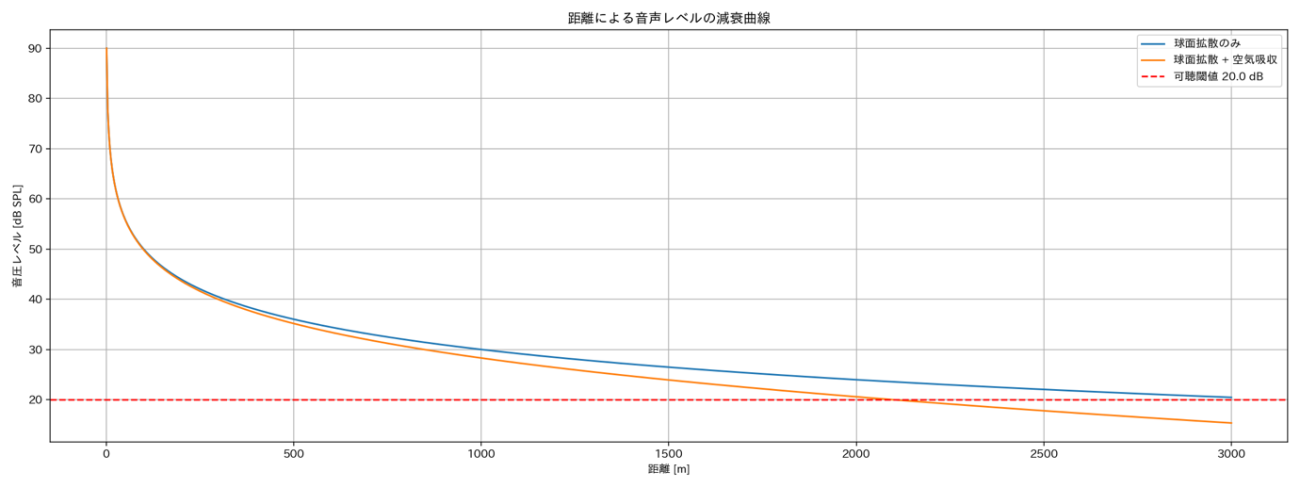
図6のように距離が遠くなって、声が広がるとともに青い線の音波のエネルギーは低下しています。
そこに自然界は無音な空間ではないために、風や足音のようにある程度の雑音が混じっています。この雑音は20dBあたりだといわれているので「ヤッホー」の声が聞き分けられる基準を20dBという閾値を設けました(図6の赤い点線)。
グラフを見ると、音波の拡散による減衰では、3000mほどで聞こえなくなるということがわかります。
さらに、先ほど算出した空気による吸収も考慮した結果がオレンジ色の線になります。
今回は、空気による吸収が少ない状態と仮定して算出することでやまびこが聞こえる最大距離がわかるため、αが小さい値で求めます。
使用した吸収係数α=0.0017は図 5の周波数400hz、湿度20%、気温15℃の時の吸収係数の値です。この吸収係数αを推察値に加えると、一般の男性の大声でも往復2000mで聞き分けることが困難である(オレンジの実線が赤い点線と交わっている)と予測できます。やまびこは往復の経路が必要なのでやまびこの反射面は1000m以内に存在する必要がありますね。

やまびことリモートセンシング技術
さて、ここからが本記事の本題です。
やまびこの条件から地形は最も重要であることを紹介しました。しかしながら現地に行ってみないと地形なんてわからないと思われる方も多いかもしれません。
そこで、現地に行かずとも活躍するリモートセンシングデータを紹介します。現地の情報を、リモートセンシングデータから再現することで、現地に行かなくても物理的な特性などをある程度用意することが可能になるのです。
では、具体的に使用するデータを紹介します。
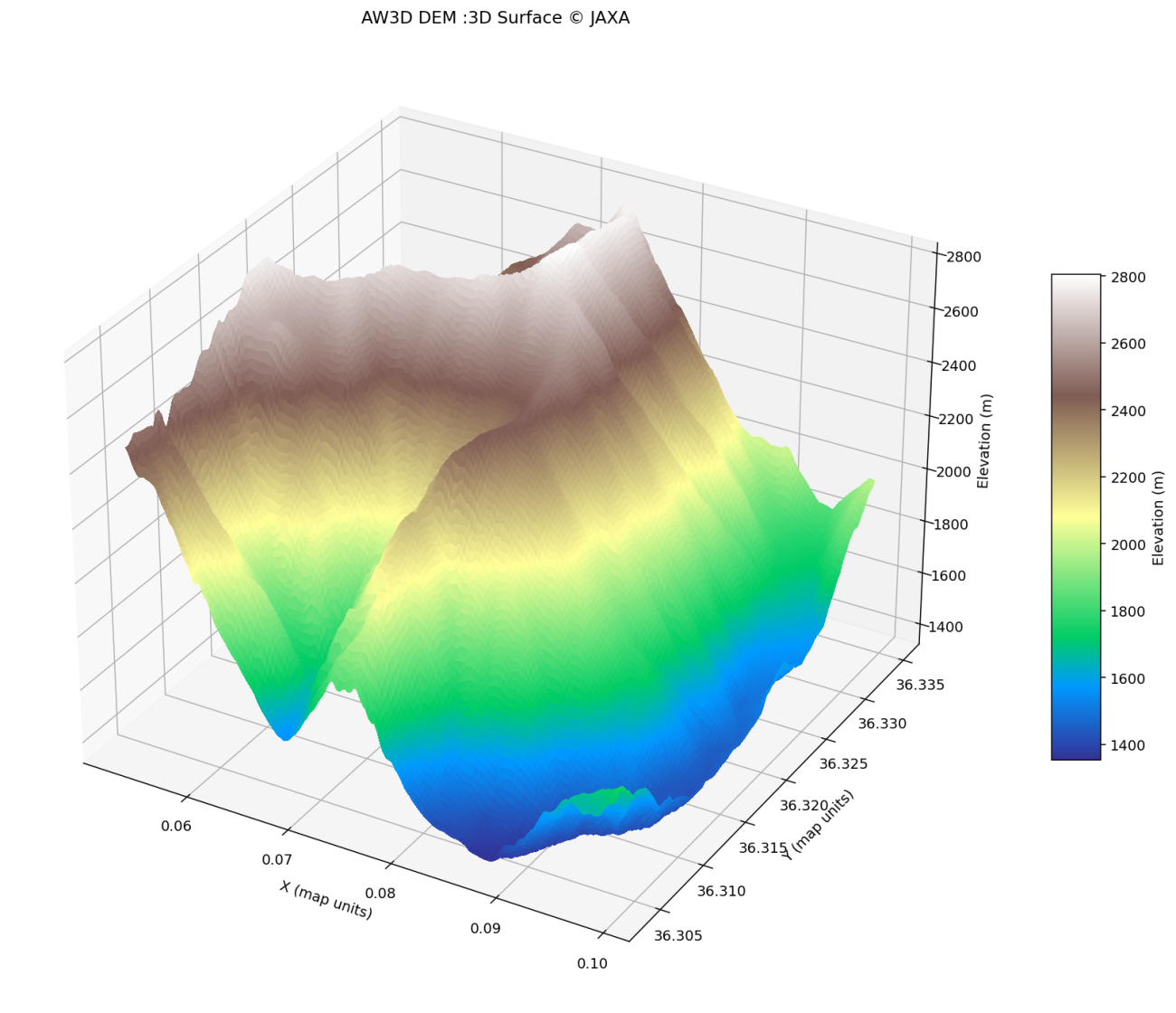
本記事では、地形情報をAW3D(ALOS World 3D)という衛星データから作成した数値標高モデル(Digital Elevation Model; DEM)を使用します。
データについてはこちらのリンクからGeoTIFF形式の取得が可能です。また、公式の全球提供情報はこちらです。
AW3Dデータは、人工衛星「ALOS」のPRISMという光学センサーによって得られた衛星画像の視差を利用することで得られた30mの空間分解能を持つ標高情報のことです。
視差は視線ベクトルという衛星から地球表面を観測する視線が異なる軌道で観測することによって得られる誤差から高さを推定する手法です。
異なる場所にカメラを2つ用意することで見える画角が変化します。その差から物体までの距離を得る技術で、人間も左右の目それぞれから得られた画像を脳が直感的に理解することで、物体がどれくらい離れているのかを把握しています。
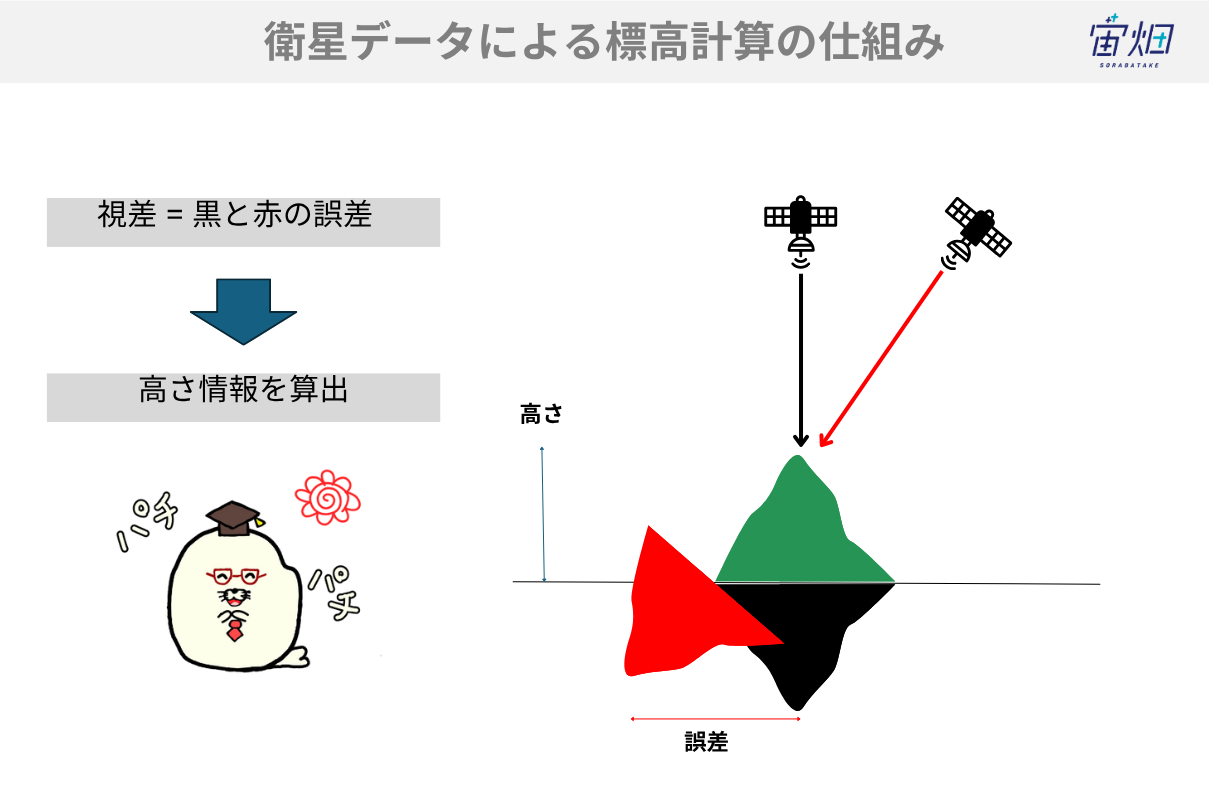
そして、今回重要なのは、AW3Dなどのデジタル標高モデル(DEM)を用いれば、山域の斜面角度や凹凸分布を定量化できるということです。
音源位置と反射候補面の法線方向(曲線や曲面と直角に交わる直線)を解析し、反射効率を数値化することで、やまびこ発生ポテンシャルを評価でき、音響モデルとの統合も可能になります。
さらに、音波追跡(ray tracing)を行い、発声点から複数の反射面までの経路と遅延時間をシミュレーションし、地形の変化やその誤差でいつ「ヤッホー」が返ってくるのも検証しながらヤッホーポイントを探しすことができます。
やまびこの現地データ
今回はライターである(安井)の同僚で、登山アプリ「YAMAP」のヘビーユーザーであるekatさん (https://yamap.com/users/1960056 )に協力を頂いて現地のやまびこが聞こえるヤッホーポイントについて教えて頂きました。

場所は笠ヶ岳の杓子平です。私もクライマーなのでわかりますが、穂高をはじめとした3000m級の山々が連なる日本アルプスは最高です。やまびこが聞こえたヤッホーポイントの詳しいGPSの位置座標は、緯度36.318、経度137.578に当たる場所とのこと。

座標投影することで地理空間的なイメージも確認しておきましょう。GeoJSON形式で保存することでGISツールを活用できるようにします。
ECHO_POINT_LATLON = (36.318,137.578)
# GeoDataFrame の作成
gdf = gpd.GeoDataFrame(
{'name': ['Echo Point']},
geometry=[Point(ECHO_POINT_LATLON[1], ECHO_POINT_LATLON[0])],
crs='EPSG:4326' # WGS84
)
gdf.to_file(
os.path.join(PATH_OUTPUT, 'echo_point.geojson'),
driver='GeoJSON')図10は、QGIS上で国土地理院の写真をベースマップとして可視化した結果です。
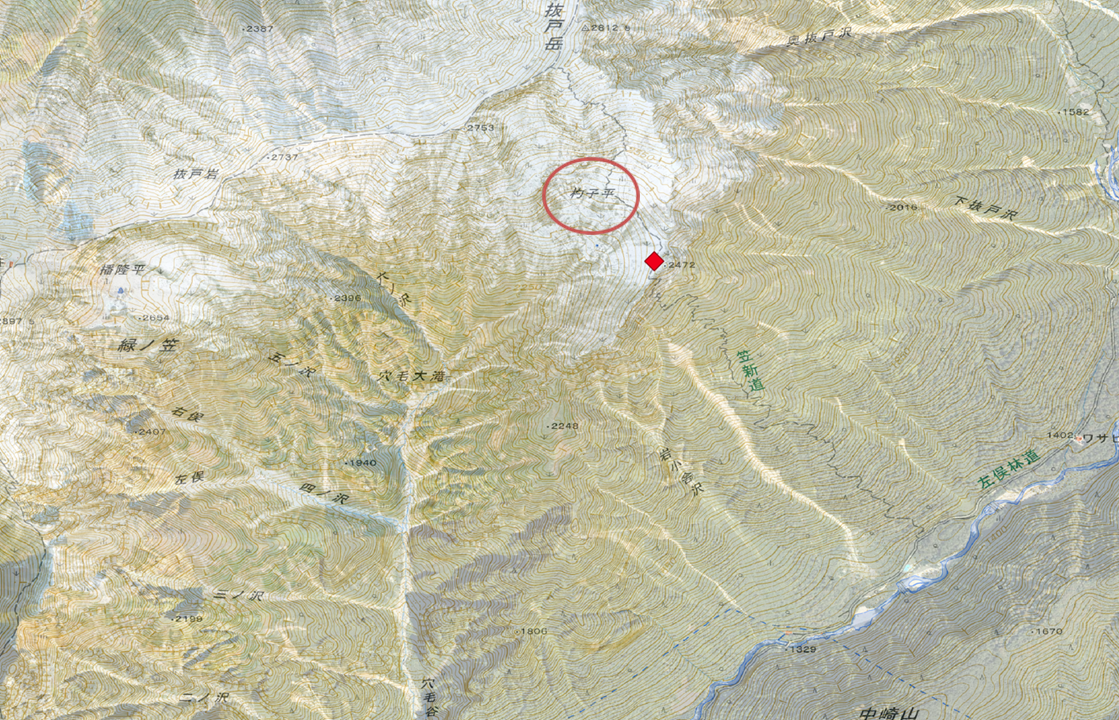
では、笠ヶ岳の詳細を見ていきましょう。図11では、国土地理院のタイルを使用して、等高線と写真を重ね合わせて可視化しています。ヤッホーポイントは杓子平の少し手前のカールに位置する場所です。
先ほどの衛星データをもとにしたAW3Dの標高データを読み込んでヤッホーポイントを可視化してみます。まずは、GeoTIFFの投影座標から画像上のピクセル座標を算出します。
PATH_DEM = os.path.join("..", 'data/aw3d_kasagatake.tif')
with rasterio.open(PATH_DEM) as ds:
raster_crs = ds.crs
nodata = ds.nodata
transform = ds.transform
dem = ds.read(1)
records = []
# Reproject to raster CRS
if gdf.crs is not None and raster_crs is not None and gdf.crs != raster_crs:
gdf = gdf.to_crs(raster_crs)
# 座標配列
xs = gdf.geometry.x.to_numpy()
ys = gdf.geometry.y.to_numpy()
# 行・列 (row, col)
rows, cols = rowcol(transform, xs, ys)
print(rows, cols)
for (i, (r, c)) in enumerate(zip(rows, cols)):
# 範囲チェック
in_bounds = (
(r >= 0) & (r = 0) & (c < ds.width)
)
print(f"有効なピクセル数: {in_bounds}")
if in_bounds:
try:
# DEM 値取得
vals = dem[r, c]
except IndexError:
vals = -1
# レコード化
rec = {
"source_file": "dem",
"feature_id": i,
"x": xs[i] if in_bounds else None,
"y": ys[i] if in_bounds else None,
"pixel_x": int(c) if in_bounds else None,
"pixel_y": int(r) if in_bounds else None,
"dem": vals if in_bounds else np.nan,
}
records.append(rec)
# DataFrame
df = pd.DataFrame.from_records(records)
df.head()
続いて、標高データと共に可視化していきます。
target_point = df.iloc[0]
dem = tifffile.imread(PATH_DEM)
# 点も同時に可視化
plt.figure(figsize=(14, 8), dpi=100, facecolor='white', edgecolor='black')
plt.imshow(dem, cmap='terrain', vmin=1200, vmax=3000)
plt.colorbar(label='標高 (m)', shrink=0.6, aspect=12)
plt.title('笠ヶ岳の標高データとヤッホーポイント © JAXA - AW3D30')
plt.xlabel('X (pixel): 30m解像度 緯度方向')
plt.ylabel('Y (pixel): 30m解像度 経度方向')
plt.scatter(target_point.pixel_x, target_point.pixel_y, color='red',
s=100, label='Yahoo Point', alpha=0.7)
plt.legend()
plt.grid(False)
plt.savefig(os.path.join(PATH_OUTPUT, 'kasagadake_yahoo.png'), bbox_inches='tight')
plt.show()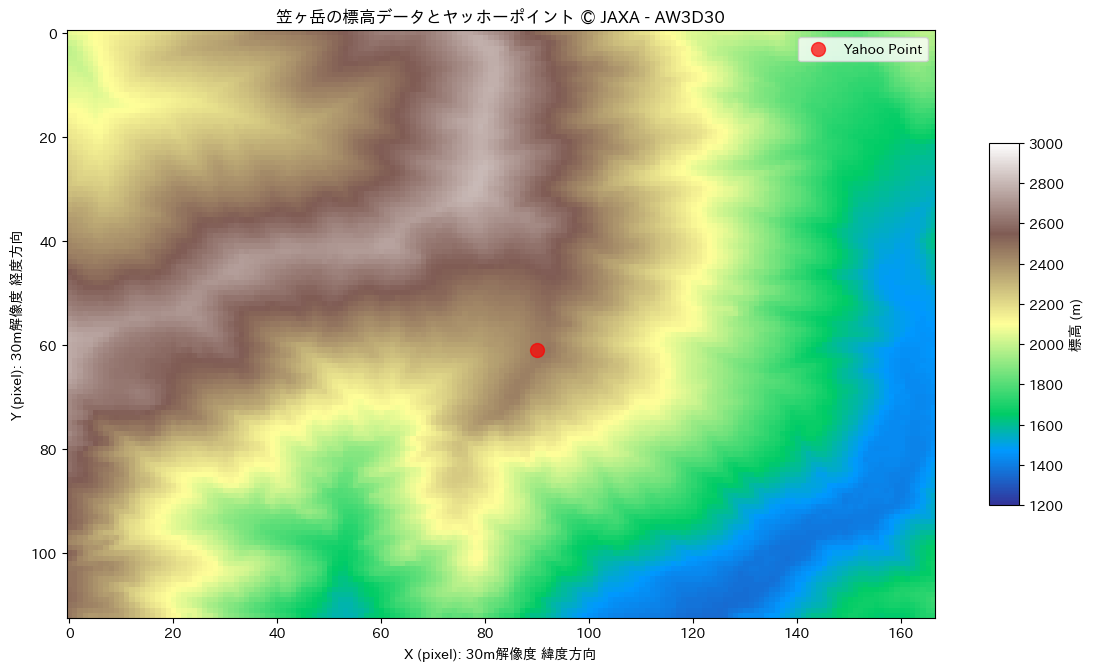
図 13のように地形と共に可視化することでヤッホーポイントがどのような場所になっているのか、様々な情報が引き出せそうですね。例えば、ヤッホーポイントは稜線上にあり、周囲はなだらかに下っていることが分かります。一方で、図 13の左上の方には3000mに近い高い山々が連なっています。

やまびこのシミュレーションをフルスクラッチで実装
ではいよいよ、地形データという三次元的な空間データと音響シミュレーションを統合するシミュレーターをPythonのフルスクラッチで実装してきます。やまびこの発生メカニズムを定量的に解析できる時代が到来しているのは本当に幸せですね。
本記事で実装したシミュレーターは以下の3つの機能を実装しています。
1.距離推定
2.反射面の特性
3.反射点の判断
1つ目の距離推定についてです。算出した秒速340mの一定の速度で音波が伝搬するとを想定して、数値標高モデルのピクセル情報から距離を求めます。発生してから反射して戻ってくるまでの経過秒数を求めることが可能で、音量の分散具合から「ヤッホー」が届く現実的な距離も計算し、条件を絞ることができます。
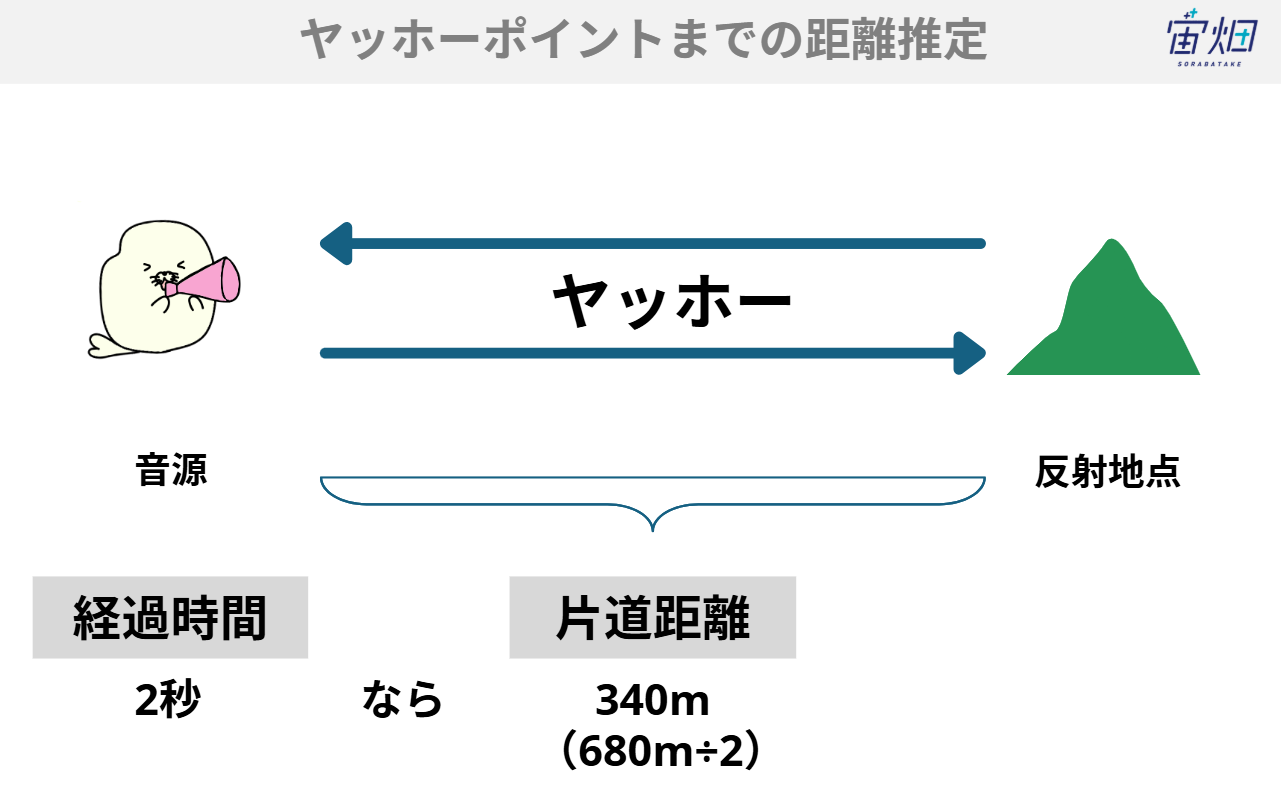
2つ目は、反射面の特性についてです。数値標高モデルから山の斜面の傾斜(スロープ)を計算できます。傾斜の方向がある程度は急な角度を持っていないと、壁のような反りたった地形になっていないため、音波を反射しないことが想像されます。また、傾斜の方角も音源に近い方向を向いていることを条件に加えています。
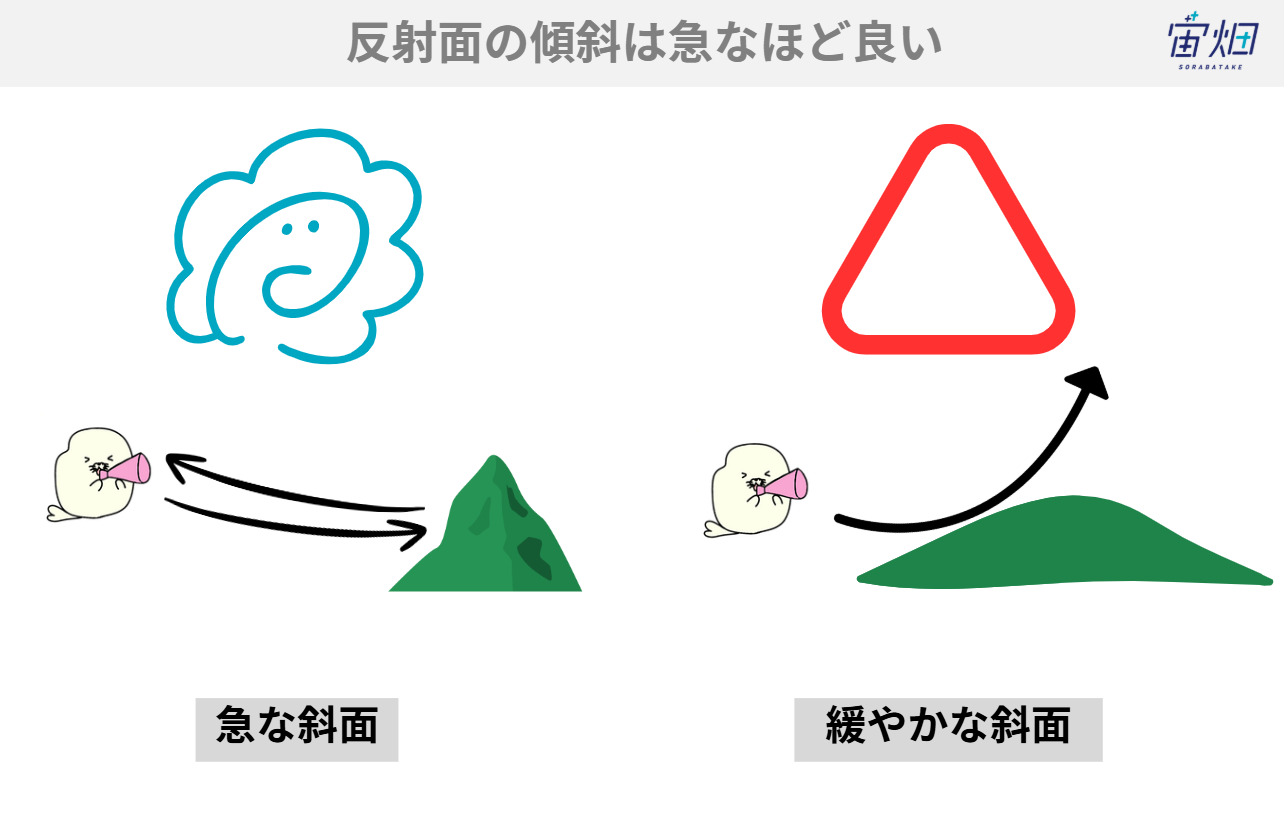
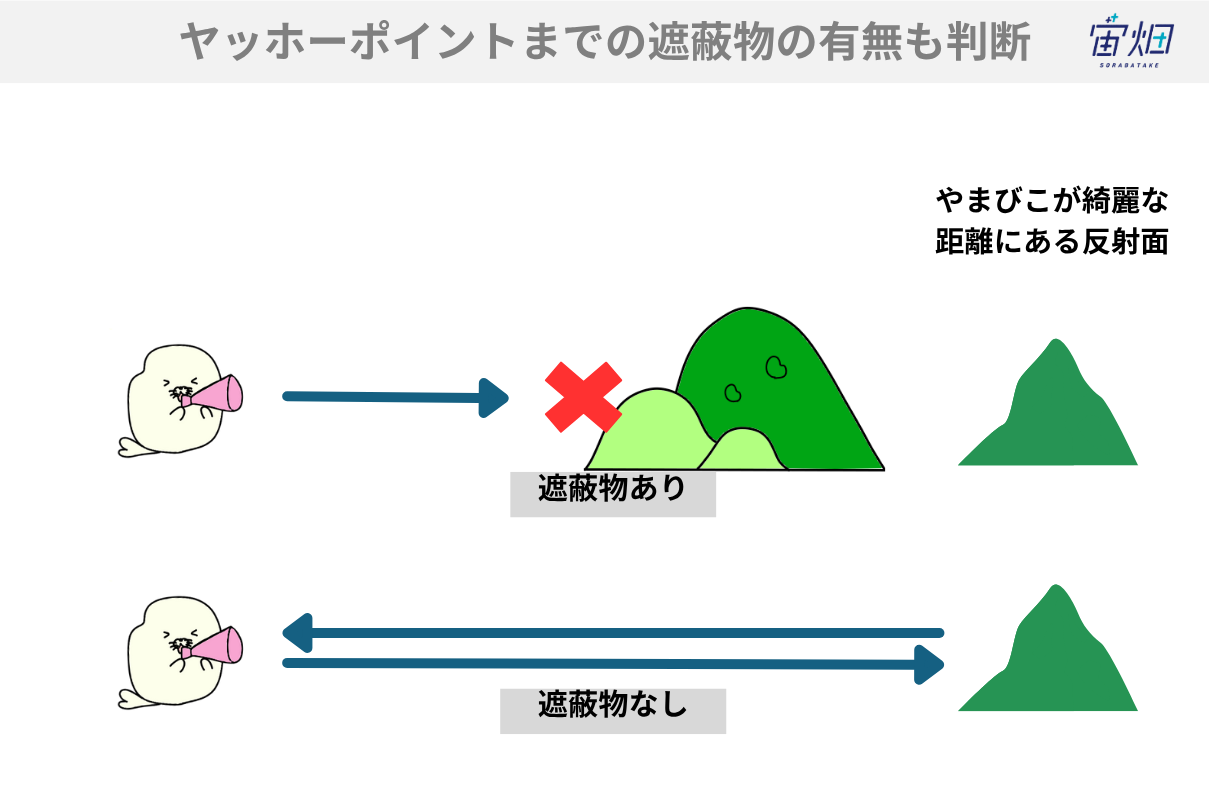
3つ目は、反射点の判断についてです。反射点になるかどうかは、1つ目と2つ目の条件だけでは、間に遮蔽物などがある場合を見逃して反射点として候補を見積もってしまします。
反射点になり得るかどうかは、間に山のような地形がないことを確かめます。そうすることで、「ヤッホー」が届くより正しい推定が出来きます。
では、これらを踏まえて実装していきます。
def calculate_slope_aspect(dem, cell_size):
"""
DEMデータから各地点の傾斜(度)と傾斜方位(度)を計算します。
"""
# NumPyのgradient関数を用いて、Y方向とX方向の標高変化を計算
# gradientは(dy, dx)の順で返すので注意
dz_dy, dz_dx = np.gradient(dem, cell_size)
# 傾斜を計算(ラジアンから度に変換)
slope = np.arctan(np.sqrt(dz_dx**2 + dz_dy**2)) * 180 / np.pi
# 傾斜方位を計算(北を0度とする地理的角度に変換)
# arctan2の引数は(y, x)の順
aspect = np.arctan2(-dz_dx, dz_dy) * 180 / np.pi
aspect = (aspect + 360) % 360
return slope, aspect
def has_line_of_sight(dem, source_pos, target_pos, source_height=1.5):
"""
DEM上の2点間に見通しがあるかを確認します。
音源の高さ(地上1.5m)を考慮します。
"""
source_elev = dem[source_pos] + source_height
target_elev = dem[target_pos]
dx = target_pos[1] - source_pos[1]
dy = target_pos[0] - source_pos[0]
# DDAアルゴリズムでライン上のセルを走査
steps = max(abs(dx), abs(dy))
if steps == 0:
return True
x_increment = dx / steps
y_increment = dy / steps
x = float(source_pos[1])
y = float(source_pos[0])
for i in range(1, int(steps)):
x += x_increment
y += y_increment
curr_x, curr_y = int(round(x)), int(round(y))
# 現在地における見通し線の標高
line_of_sight_elev = source_elev + (target_elev - source_elev) * (i / steps)
# 現在地の地形の標高
terrain_elev = dem[curr_y, curr_x]
# 地形が見通し線を遮っていればFalse
if terrain_elev > line_of_sight_elev:
return False
return True
def simulate_echo(dem, source_pos,
cell_size=10,
sound_speed=340.29,
max_distance=340 * 5,
max_angle=45.):
"""
DEMの中心を音源として、やまびこの可能性をシミュレーションします。
Args:
dem (np.ndarray): 地形標高モデル(DEM)を表す2次元NumPy配列。
source_pos (tuple): 音源の位置を表すタプル (row, col) (y, x)。
cell_size (int): DEMの1セルの実際の辺の長さ(メートル)。
sound_speed (float): 音速 (m/s)。
max_distance (int): やまびこが認識される最大距離(メートル)。
max_angle (float): やまびこが認識される最大角度(度)。
Returns:
list: やまびこの可能性がある地点の情報を格納した辞書のリスト。
"""
height, width = dem.shape
potential_echoes = []
# 地形全体の傾斜と傾斜方位を事前に計算
slopes, aspects = calculate_slope_aspect(dem, cell_size)
for r in range(height):
for c in range(width):
if (r, c) == source_pos:
# 同一点の無視
continue
if slope_at_target max_angle:
# print(f"傾斜方位が合わない: {aspect_at_target} vs {angle_to_source} (差: {angle_diff:.2f}度)")
continue
# 3. 見通しの確認
if not has_line_of_sight(dem, source_pos, target_pos, source_height=10):
# print(f"見通しがない: {source_pos} -> {target_pos}")
continue
# 全ての条件を満たした場合、やまびこの候補とする
delay_time = (2 * distance) / sound_speed
potential_echoes.append({
"position": target_pos,
"distance_m": distance,
"delay_s": delay_time,
"slope_deg": slope_at_target,
})
return potential_echoes, slopes
target_pos = (r, c)
# 1. 距離の確認
distance = math.sqrt((r - source_pos[0])**2 + (c - source_pos[1])**2) * cell_size
# やまびことして認識できる適切な距離に限定
if not ( 34 < distance < max_distance):
# print(f"距離が不適切: {distance:.2f} m (位置: {target_pos})")
continue
# 2. 反射面の特性を確認
# 急な斜面(例: 30度以上)を反射面と仮定
slope_at_target = slopes[target_pos]
このシミュレーターを動作させてみて、シミュレーション結果を可視化してみます。
# --- 指定されたDEMファイルの読み込み ---
dem_data = tifffile.imread(PATH_DEM)
cell_dim = 30 # AW3D 30 # 30m解像度
# --- シミュレーション条件 ---
pixel_x, pixel_y = target_point.pixel_x, target_point.pixel_y
source_x, source_y = pixel_x * cell_dim, pixel_y * cell_dim
print(f"音源位置: ({source_x}, {source_y}) (標高: {target_point.dem} m)")
# --- シミュレーションの実行 ---
echoes, slopes = simulate_echo(
dem_data,
source_pos=(pixel_y, pixel_x),
cell_size=cell_dim,
max_angle=80, # 反射面の傾斜方位の許容角度
)
# --- 結果の表示 ---
if echoes:
print(f"\n{len(echoes)}個のやまびこの可能性を検出しました:")
# 距離が近い順にソートして表示
for echo in sorted(echoes, key=lambda x: x['distance_m']):
print(
f" - 反射位置: {echo['position']}, "
f"距離: {echo['distance_m']:.1f} m, "
f"遅延時間: {echo['delay_s']:.2f} 秒, "
f"斜面傾斜: {echo['slope_deg']:.1f}度"
)
else:
print("\nやまびこが聞こえる可能性のある地点は見つかりませんでした。")
# --- 可視化 ---
fig, ax = plt.subplots(2, 2, figsize=(24, 14), facecolor="w", dpi=140, edgecolor="k")
# DEMとやまびこ経路の可視化
grid_size_y, grid_size_x = dem_data.shape
im = ax[0, 0].imshow(dem_data, cmap='terrain', origin='upper',
extent=[0, grid_size_x * cell_dim, grid_size_y * cell_dim, 0])
ax[0, 0].set_title("地形モデル(DEM)とやまびこ経路の予測")
ax[0, 0].plot(source_x, source_y, '*', markersize=12, label='音源', color='red')
# 検出されたやまびこ候補を描画
for echo in echoes:
target_x, target_y = echo['position'][1] * cell_dim, echo['position'][0] * cell_dim
ax[0, 0].plot(target_x, target_y, 'ro', markersize=4, alpha=0.6)
ax[0, 0].plot([source_x, target_x], [source_y, target_y], 'r--', linewidth=0.5, alpha=0.5)
# 凡例用のダミープロット
if echoes:
ax[0, 0].plot([], [], 'bo', markersize=6, label='反射点候補')
ax[0, 0].legend()
ax[0, 0].set_xlabel("X座標 (m)")
ax[0, 0].set_ylabel("Y座標 (m)")
fig.colorbar(im, ax=ax[0, 0], label='標高 (m)', shrink=0.5)
im = ax[1, 0].imshow(slopes, cmap='coolwarm', origin='upper',
extent=[0, grid_size_x * cell_dim, grid_size_y * cell_dim, 0])
ax[1, 0].plot(source_x, source_y, '*', markersize=12, label='音源', color='black')
ax[1, 0].set_title("地形の傾斜(度)")
ax[1, 0].set_xlabel("X座標 (m)")
ax[1, 0].set_ylabel("Y座標 (m)")
fig.colorbar(im, ax=ax[1, 0], label='傾斜 (度)', shrink=0.5)
# 音源を通る断面図の可視化
ax[0, 1].plot(np.arange(grid_size_x) * cell_dim, dem_data[grid_size_y // 2, :],
label='東西断面', color='b')
ax[0, 1].axvline(x=source_x, color='r', linestyle='--', label='音源位置')
ax[0, 1].set_title("音源位置を通る地形断面図")
ax[0, 1].set_xlabel("距離 (m)")
ax[0, 1].set_ylabel("標高 (m)")
ax[0, 1].legend()
ax[0, 1].grid(True)
# 音源を通る断面図の可視化
ax[1, 1].plot(np.arange(grid_size_y) * cell_dim, dem_data[:, grid_size_x // 2],
label='南北断面', color='orange')
ax[1, 1].axvline(x=source_x, color='r', linestyle='--', label='音源位置')
ax[1, 1].set_title("音源位置を通る地形断面図")
ax[1, 1].set_xlabel("距離 (m)")
ax[1, 1].set_ylabel("標高 (m)")
ax[1, 1].legend()
ax[1, 1].grid(True)
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'kasagadake_echo_simulation.png'), bbox_inches='tight')
plt.show();
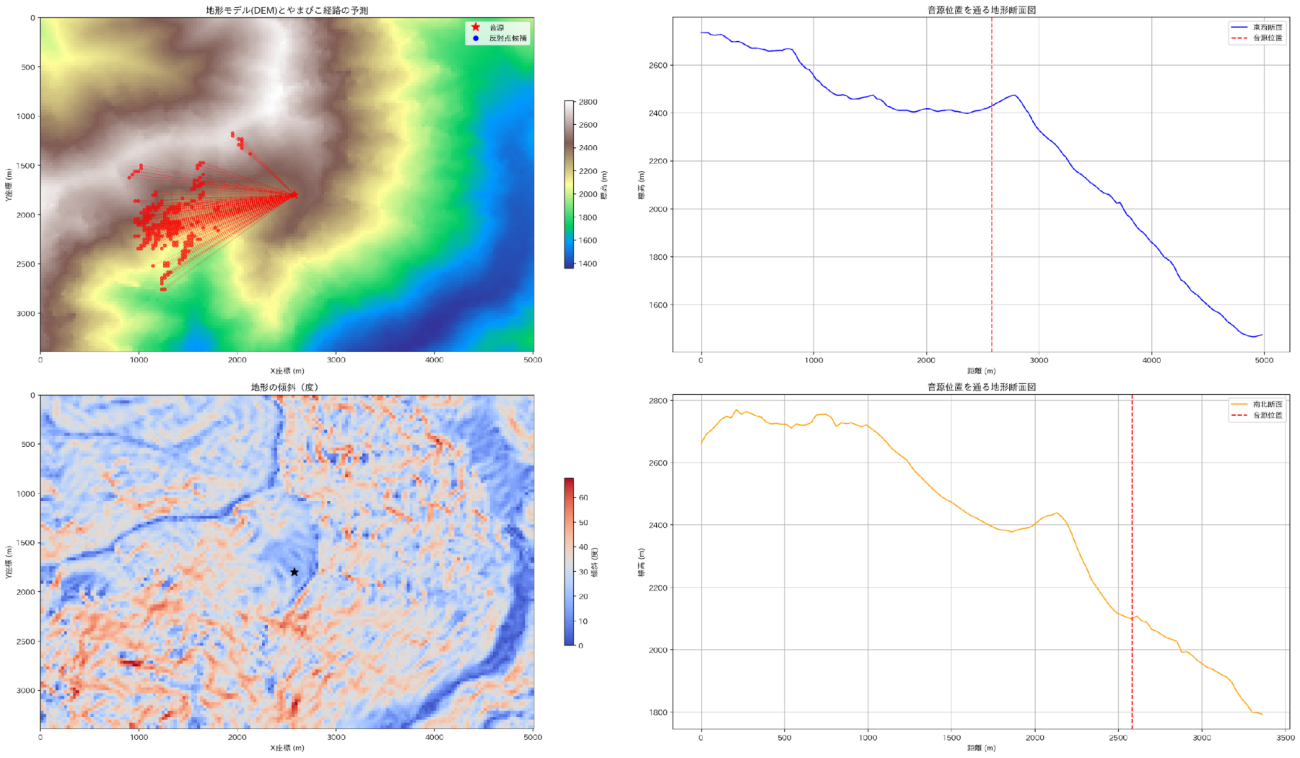
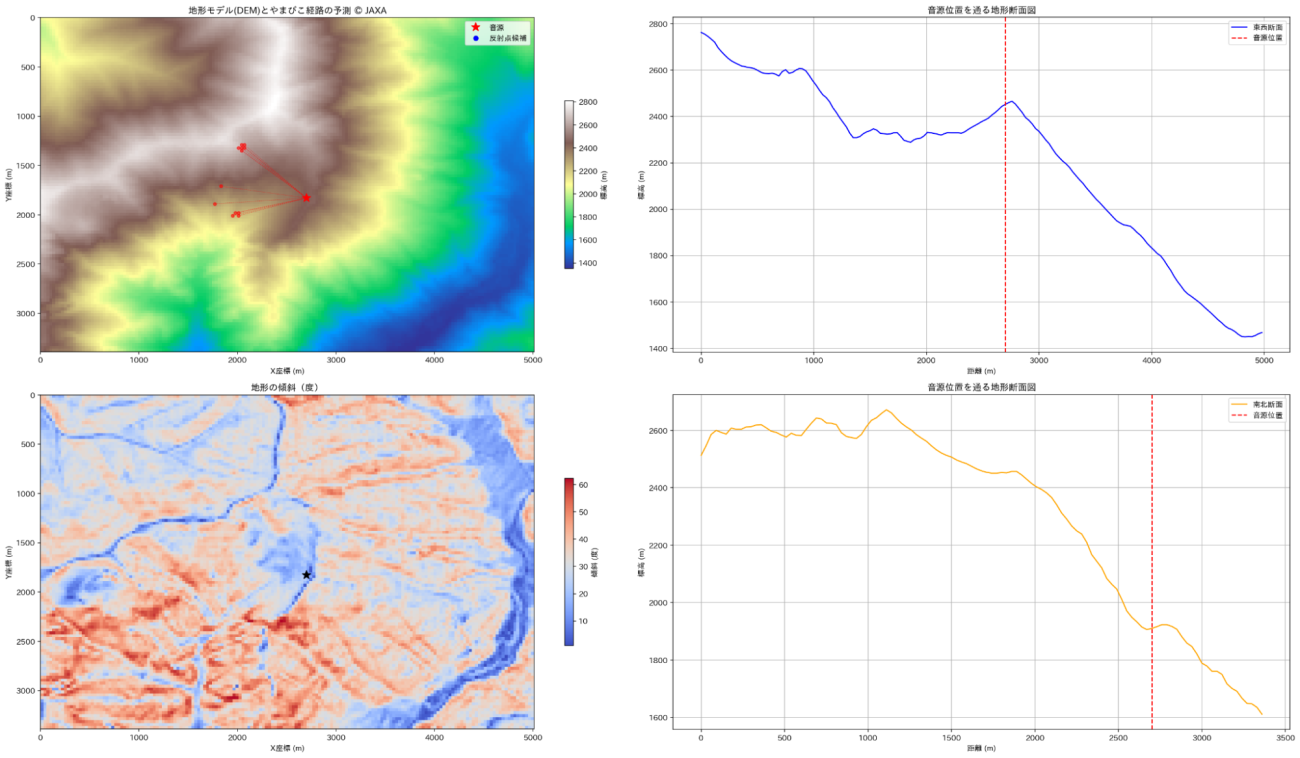
plt.clf();plt.close('all')音源位置: (2700, 1830) (標高: 2452 m)
173個のやまびこの可能性を検出しました
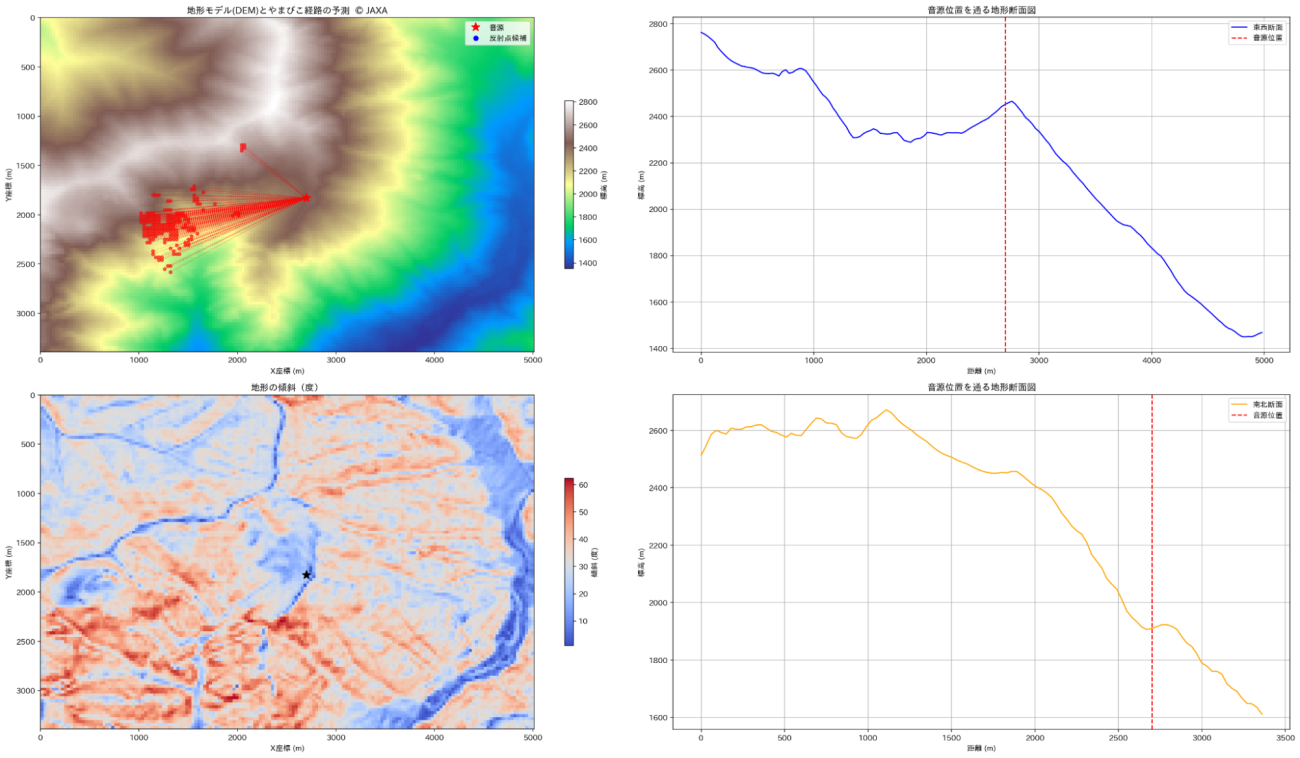
左上:地形と音源と反射点の位置関係
左下:地形情報から算出した傾斜情報
右上:音源の東西方向の地形プロファイル
右下:音源の南北方向の地形プロファイル Credit : JAXA
左上の図が、遮蔽物や音源を発した先にある反射点の坂が緩やかで反射しないと想定される場所を除外した結果です。西側に条件に合致する反射点が集まっているように見えます。
伝搬する様子も可視化してみましょう。
# 音源の位置(m)
src_x, src_y = df.loc[0, ["source_x", "source_y"]]
src_x *= cell_dim
src_y *= cell_dim
# 反射点の位置(m)
tgt_xy_m = np.column_stack([
df["position_x"].values * cell_dim,
df["position_y"].values * cell_dim,
])
# pixel 差分
dx_pix = (tgt_xy_m[:, 0] - src_x) / cell_dim
dy_pix = (tgt_xy_m[:, 1] - src_y) / cell_dim
speed_mps = np.where(
(dx_pix != 0) & (dy_pix != 0),
cell_dim, # 30
cell_dim # 30
)
# 片道距離と所要時間
dist_m = np.hypot(tgt_xy_m[:, 0] - src_x, tgt_xy_m[:, 1] - src_y)
time_one_leg = dist_m / speed_mps # [s] 片道
time_round = 2 * time_one_leg # [s] 往復
# ------------------------------
# アニメーション設定
# ------------------------------
fps = 2 # 描画フレームレート
dt = 1.0 / fps # 1フレームの時間 [s]
t_max = time_round.max() # 最長の往復時間
frames_tot = int(np.ceil(t_max / dt)) + 1
fig, ax = plt.subplots(figsize=(10, 8), dpi=140, facecolor="w")
gs_y, gs_x = dem_data.shape
ax.imshow(
dem_data, cmap="terrain", origin="upper",
extent=[0, gs_x * cell_dim, gs_y * cell_dim, 0],
)
ax.set_title("やまびこシミュレーション")
ax.set_xlabel("X 座標: 緯度 [m]")
ax.set_ylabel("Y 座標: 経度 [m]")
ax.plot(src_x, src_y, "*", ms=12, color="orange", label="音源")
for i, (tx, ty) in enumerate(tgt_xy_m):
if i == 0:
ax.plot(tx, ty, "ro", ms=4, alpha=0.6, label="反射点")
else:
ax.plot(tx, ty, "ro", ms=4, alpha=0.6) # 反射点
ax.plot([src_x, tx], [src_y, ty], "r--", lw=0.6, alpha=0.4) # 経路
# 動く点を反射点の数だけ生成
color_range = np.linspace(0.3, 0.9, len(tgt_xy_m)) # 最後の点はラベル用
blue_colors = plt.cm.Blues(color_range)
moving_dots = [
ax.plot([], [], "o", ms=7, color=blue_colors[i], alpha=0.6)[0] for i in range(len(tgt_xy_m)-1)
] + [
ax.plot([], [], "o", ms=7, color=blue_colors[-1], label="声(ヤッホー)")[0]
] # 最後の点はラベル用
ax.legend()
pbar = tqdm(total=frames_tot, desc="Animating", ncols=70)
def init():
for dot in moving_dots:
dot.set_data([], [])
return moving_dots
def update(frame):
t_now = frame * dt # 経過秒
for i, dot in enumerate(moving_dots):
T = time_one_leg[i]
# 0‥T : forward、T‥2T : backward、それ以降は停止
if t_now <= 2 * T:
if t_now <= T: # 往路
tau = t_now / T
else: # 復路
tau = 2 - t_now / T
x = src_x + tau * (tgt_xy_m[i, 0] - src_x)
y = src_y + tau * (tgt_xy_m[i, 1] - src_y)
dot.set_data(x, y)
else:
dot.set_data([], []) # 座標リセット
dot.set_visible(False) # 完全非表示
pbar.update(1)
if frame == frames_tot - 1: # 最終フレームでバーを閉じる
pbar.close()
return moving_dots
ani = FuncAnimation(
fig, update,
frames=frames_tot,
init_func=init,
blit=True,
interval=1000 / fps,
repeat=True,
)
ani.save(
os.path.join(PATH_OUTPUT, "echoes_all_points.mp4"),
writer=FFMpegWriter(fps=30))
plt.tight_layout()
plt.show()音波の伝搬をアニメーションで確認することで反射のタイミングと場所は直感的にも推移してそうですね。

シミュレーション結果の解析
シミュレーションによって反射する地点の情報を取得できたので整理して可視化していきます。詳しく整理することでデータの示唆やシミュレーションの理解にも繋がります。
まずは、反射した点の方位と経過時間を可視化します。
df = pd.DataFrame({
"position_x": [echo['position'][1] for echo in echoes],
"position_y": [echo['position'][0] for echo in echoes],
"source_x": source_x / cell_dim,
"source_y": source_y / cell_dim,
"distance_m": [echo['distance_m'] for echo in echoes],
"delay_s": [echo['delay_s'] for echo in echoes],
"slope_deg": [echo['slope_deg'] for echo in echoes]
})
# 反射波の帰ってきた方向xyを得る
df['direction_x'] = - df['position_x'] + df['source_x']
df['direction_y'] = - df['position_y'] + df['source_y']
# angle xy
df['angle_xy'] = np.arctan2(df['direction_y'], df['direction_x']) * 180 / np.pi
df['angle_xy'] = (df['angle_xy'] - 90) % 360
df.index.name = "sample_idx" # 行番号=時系列順のインデックス
BIN_SIZE = 10 # お好みで 5, 15, 30 などに変更可
df["angle_bin"] = (df["angle_xy"] // BIN_SIZE * BIN_SIZE).astype(int)
table = df.pivot_table(index="sample_idx",
columns="angle_bin",
values="delay_s")
# plot delay vs angle
plt.figure(figsize=(16, 5), dpi=140, facecolor="w", edgecolor="k")
plt.scatter(df['angle_xy'] , df['delay_s'], alpha=0.8)
plt.title('Delay vs Angle of Echoes')
plt.xlabel('Angle (degrees)')
plt.ylabel('Delay (seconds)')
plt.xlim(-10, 370)
plt.grid(True)
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'delay_vs_angle.png'), bbox_inches='tight')
plt.show();plt.clf();plt.close('all')
plt.figure(figsize=(14, 5), dpi=140, facecolor="w", edgecolor="k")
plt.hist(df['delay_s'], bins=20, color='blue', alpha=0.7, edgecolor='black')
plt.title(f'Histogram of Echo Delays (Bin Size: {BIN_SIZE}°)')
plt.xlabel('Delay (seconds)')
plt.ylabel('Count')
plt.xlim(0, df['delay_s'].max() + 1)
plt.grid(axis='y')
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'echo_delay_histogram.png'), bbox_inches='tight')
plt.show();plt.clf();plt.close('all')
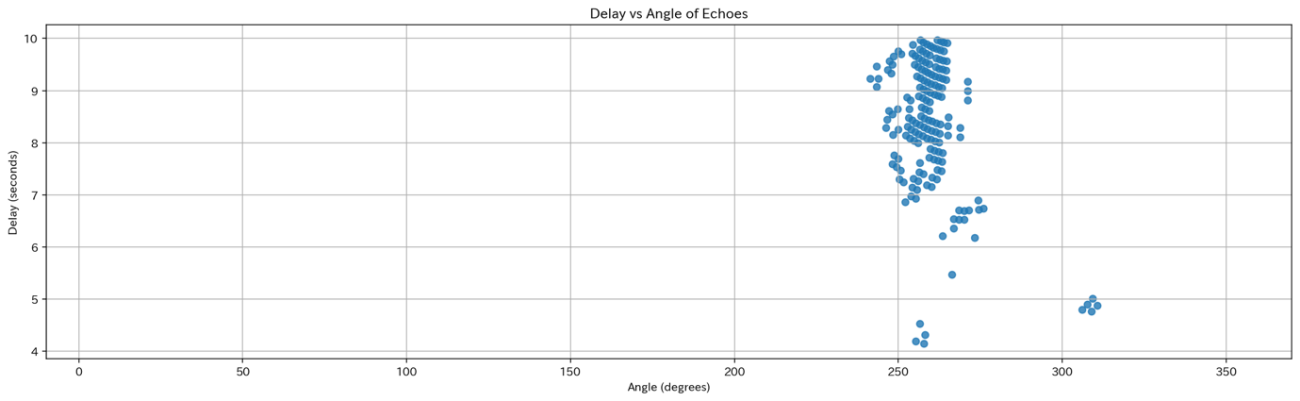
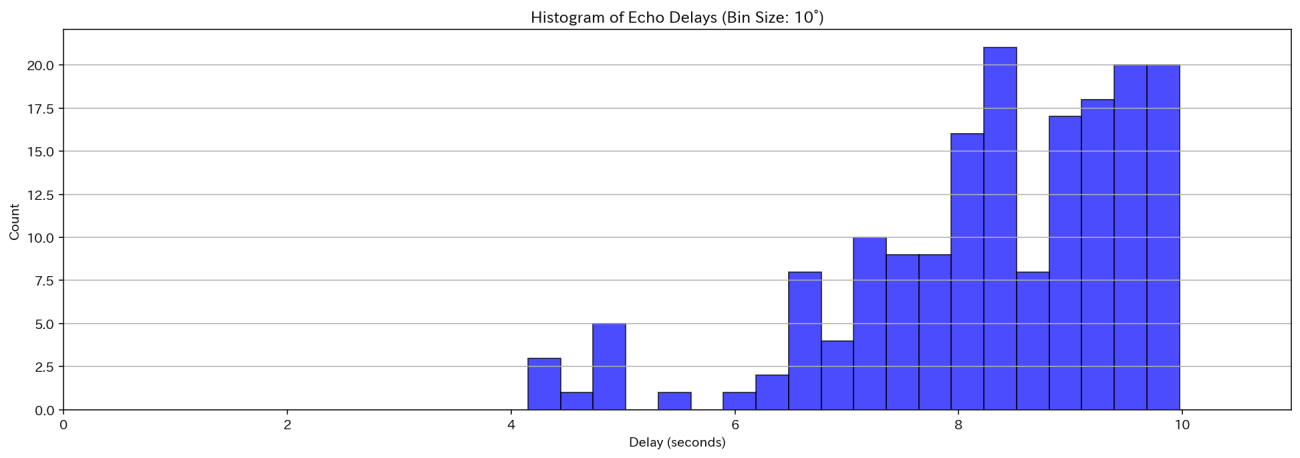
結果を確認すると、発生から4秒〜10秒の間に「ヤッホー」が返ってくると分かります。また、方角は北を0°として時計回りに角度 260°あたりに集中しています。タイミングがズレると、反響が弱くなったりするので注意です。
声の距離と方位のまとまりをクラスター分類で可視化してみます。
# 特徴量行列
X = df[['angle_xy', 'delay_s']].to_numpy()
# 共分散とその逆行列
cov = np.cov(X, rowvar=False)
VI = np.linalg.pinv(cov) # np.linalg.inv でもよいが数値安定性のため pinv
# eps の設定目安:
eps = 0.2 # 必要に応じて調整
db = DBSCAN(
eps=eps,
min_samples=1,
metric='mahalanobis',
metric_params={'VI': VI}
)
labels = db.fit_predict(X)
df['cluster'] = labels
plt.figure(figsize=(14, 5), dpi=140, facecolor="w", edgecolor="k")
scatter = plt.scatter(df['angle_xy'], df['delay_s'], c=df['cluster'], cmap='Set1', alpha=0.7)
plt.title('Echoes Colored by Cluster (Mahalanobis Distance)')
plt.xlabel('Angle (degrees)')
plt.ylabel('Delay (seconds)')
plt.xlim(-10, 370)
plt.colorbar(scatter, label='Cluster ID',shrink=0.5)
plt.grid(True)
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'echo_clusters.png'), bbox_inches='tight')
plt.show()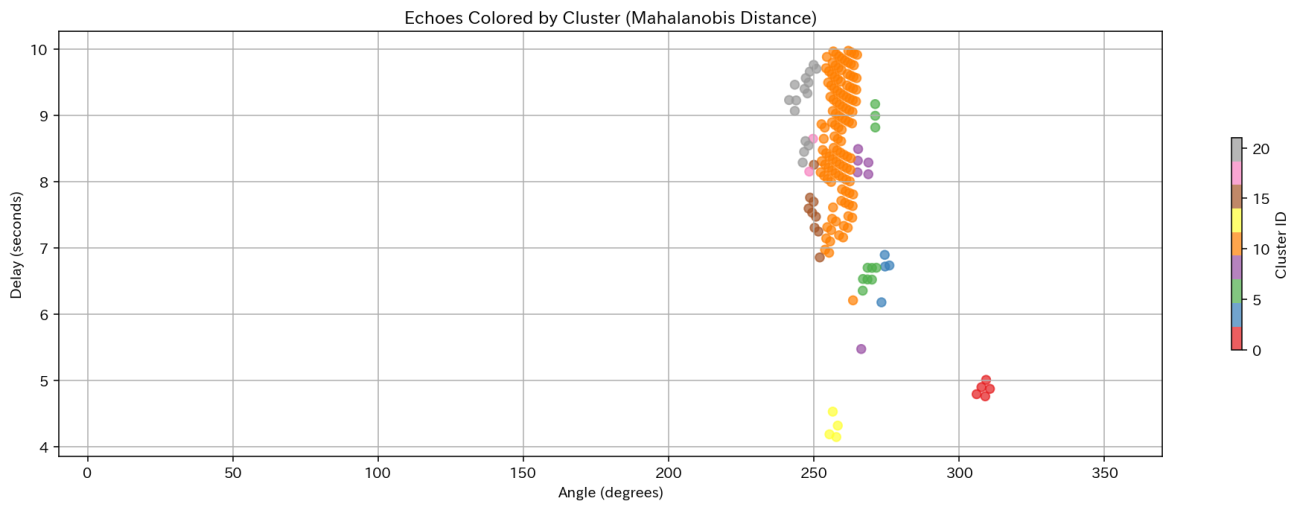
図 20からクラスター分類では、オレンジ色のサンプルが多く、やまびこの地点として期待ができそうな結果になっています。
方位の情報は分かりにくいのである角度ごとに集約してレーダープロットで可視化してみます。
bins = np.arange(0, 360 + BIN_SIZE, BIN_SIZE)
hist, edges = np.histogram(df["angle_xy"], bins=bins)
plt.figure(figsize=(16, 6), dpi=140, facecolor="w", edgecolor="k")
plt.bar(edges[:-1], hist,
width=BIN_SIZE,
align="edge",
edgecolor="black")
plt.xlabel("Azimuth bin [deg]")
plt.ylabel("Echo count")
plt.title(f"Echo count per {BIN_SIZE}° azimuth bin")
plt.xticks(edges[:-1] + BIN_SIZE / 2,
[f"{int(e)}–{int(e + BIN_SIZE)}" for e in edges[:-1]],
rotation=90)
plt.grid(axis="y", linestyle="--", linewidth=0.5)
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'echo_azimuth_histogram.png'), bbox_inches='tight')
plt.show();plt.clf();plt.close('all')
theta = np.deg2rad(edges[:-1])
width = np.deg2rad(BIN_SIZE)
fig = plt.figure(figsize=(14, 8), dpi=140, facecolor="w", edgecolor="k")
ax = fig.add_subplot(111, projection="polar")
ax.bar(theta,
hist,
width=width,
bottom=0,
align="edge",
edgecolor="black")
ax.set_theta_zero_location("N") # 0° = 北
ax.set_theta_direction(-1) # 時計回り
ax.set_title("Azimuth distribution of echoes", va="bottom")
plt.savefig(os.path.join(PATH_OUTPUT, 'echo_azimuth_histogram_polar.png'), bbox_inches='tight')
plt.show();plt.clf();plt.close('all')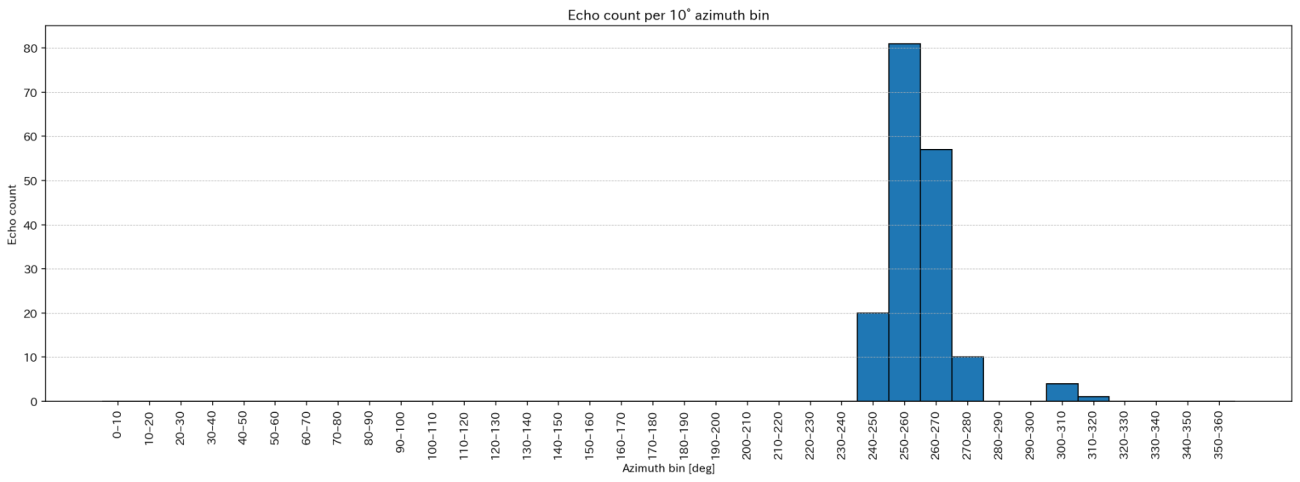
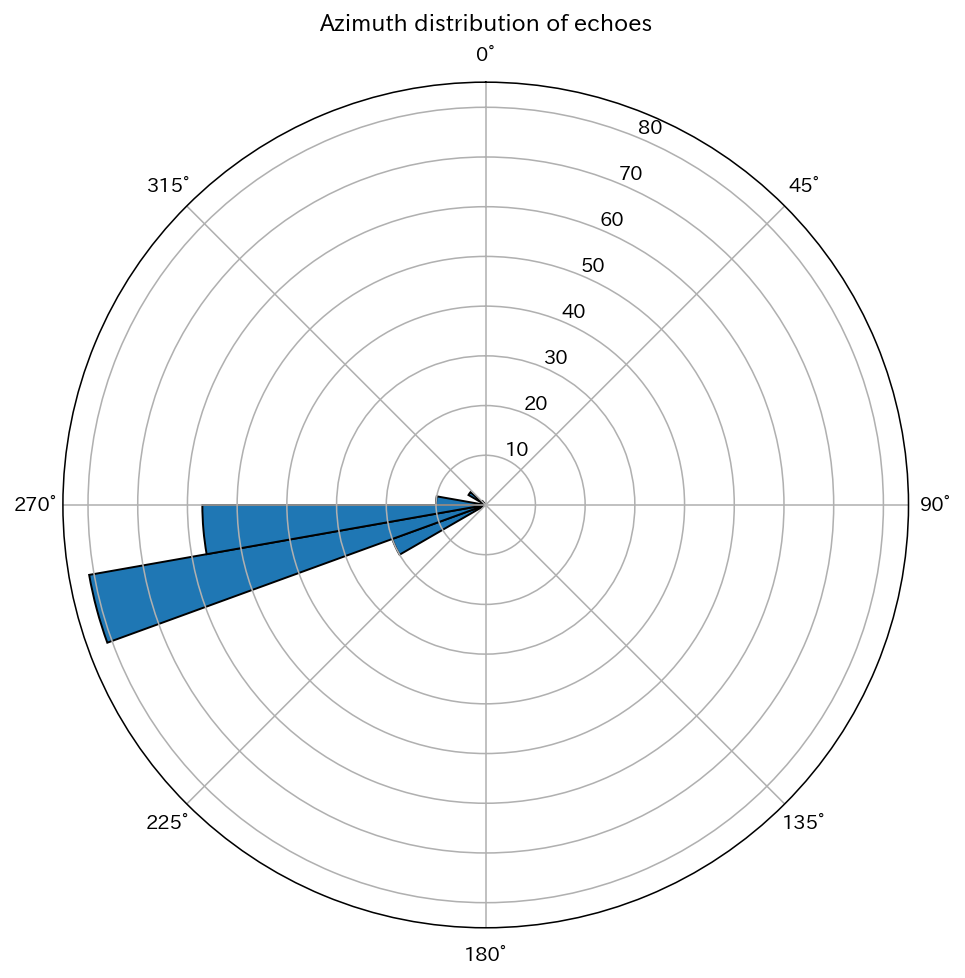
図 22のように、10°毎で集約すると 250°〜270°での反射が多いことがわかりました。距離が数秒と大きな誤差があるので反響して歪んだような「ヤッホー」が聞こえるのかな?などと予測ができそうです。
しかしながら、後述する理由で、250°〜270°への発声はやまびこが届かないと分かります。すでにここまでに紹介した中にヒントが隠されていますので、ぜひ予想しながら読み進めてみてください。

やまびこの地理空間解析
これまでは画像上での分析でしたが、再び空間投影の処理を施すことで地理空間的な解析や考察も可能になります。シミュレーションした結果を、標高データのGeoTIFFの空間情報を元に座標投影していきましょう。
まずは、ジオコードする関数の定義です。
def pixel_to_lonlat(src, x_pix: int, y_pix: int):
"""
ピクセル座標 (x_pix, y_pix) → 経度・緯度 (lon, lat) へ変換するヘルパ。
Rasterio では (row, col) = (y, x) の順なので注意。
"""
# GeoTIFF の CRS で座標を取得
lon_src, lat_src = src.xy(row=y_pix, col=x_pix, offset="center")
# 必要なら EPSG:4326 に再投影
if src.crs.to_epsg() != 4326:
lon_dst, lat_dst = reproject_pts(
src.crs, "EPSG:4326", [lon_src], [lat_src]
)
lon_src, lat_src = lon_dst[0], lat_dst[0]
return lon_src, lat_src
def circle_polygon(
lon: float,
lat: float,
radius_m: float = 30.0,
n_vertices: int = 64,
):
"""
半径[m]でバッファした円を多角形近似し、GeoJSON Polygon座標を返します。
戻り値: [ [ [lon1,lat1], ..., [lon1,lat1] ] ]
"""
cx, cy = (lon, lat)
ring = []
for i in range(n_vertices):
th = 2 * math.pi * i / n_vertices
x = cx + radius_m * math.cos(th)
y = cy + radius_m * math.sin(th)
lon_i, lat_i = (x, y)
ring.append([lon_i, lat_i])
ring.append(ring[0])
return [ring]そして、シミュレーション結果をベクターデータとして、GeoJSON形式で保存します。ここでは、音源を円ポリゴン、反射点を点ポリゴン、音源と反射点をラインストリングの線で格納する処理です。
features = []
radius_m: float = 30.0 * 1e-5
with rasterio.open(PATH_DEM) as src:
row = df.iloc[0]
x_pix, y_pix = row['source_x'], row['source_y']
lon, lat = pixel_to_lonlat(src, x_pix, y_pix)
# 円ポリゴンのGeoJSON形式
features.append(
{
"type": "Feature",
"geometry": {
"type": "Polygon",
"coordinates": circle_polygon(lon, lat, radius_m),
},
"properties": {
"pixel_x": x_pix,
"pixel_y": y_pix,
"name": "Kasagadake Echo Point",
"radius_m": radius_m,
},
}
)
for i, (x_pix, y_pix, x_pos, y_pos, delay_s, angle_xy, clus) in enumerate(
zip(df['source_x'], df['source_y'], df['position_x'], df['position_y'],
df['delay_s'], df['angle_xy'], df['cluster'])):
lon_src, lat_src = pixel_to_lonlat(src, x_pix, y_pix)
lon_pos, lat_pos = pixel_to_lonlat(src, x_pos, y_pos)
sec_str = f"{delay_s:.1f}秒"
features.append(
# pointのGeoJSON形式
{
"type": "Feature",
"geometry": {
"type": "Point",
"coordinates": [lon_pos, lat_pos], # GeoJSON は (lon, lat) 順
},
"properties": {
"pixel_x": x_pos,
"pixel_y": y_pos,
"name": "Reflection Point",
"cluster": clus,
"delay_s": delay_s,
"delay_str": sec_str,
"angle_xy": angle_xy,
},
})
# 反射位置の座標
features.append(
# position -> source の LineString
{
"type": "Feature",
"geometry": {
"type": "LineString",
"coordinates": [
[lon_src, lat_src], # 音源位置
[lon_pos, lat_pos] # 反射位置
]
},
"properties": {
"source_x": x_pix,
"source_y": y_pix,
"position_x": x_pos,
"position_y": y_pos,
"delay_s": delay_s,
"delay_str": sec_str,
"angle_xy": angle_xy,
"cluster": clus,
"name": "Echo Trace",
}
},
)
fc = {"type": "FeatureCollection", "features": features}
# 保存
out_path = os.path.join(PATH_OUTPUT, 'kasagadake_echoes.geojson')
out_path = Path(out_path)
out_path.write_text(json.dumps(fc, ensure_ascii=False, indent=2))
print(f"✅ GeoJSON 保存完了: {out_path.resolve()}")
df.to_csv(os.path.join(PATH_OUTPUT, 'kasagadake_echoes.csv'), index=False)
print(f"✅ CSV 保存完了: {os.path.join(PATH_OUTPUT, 'kasagadake_echoes.csv')}")では、製作したGeoJSONをQGIS上で可視化してみましょう。
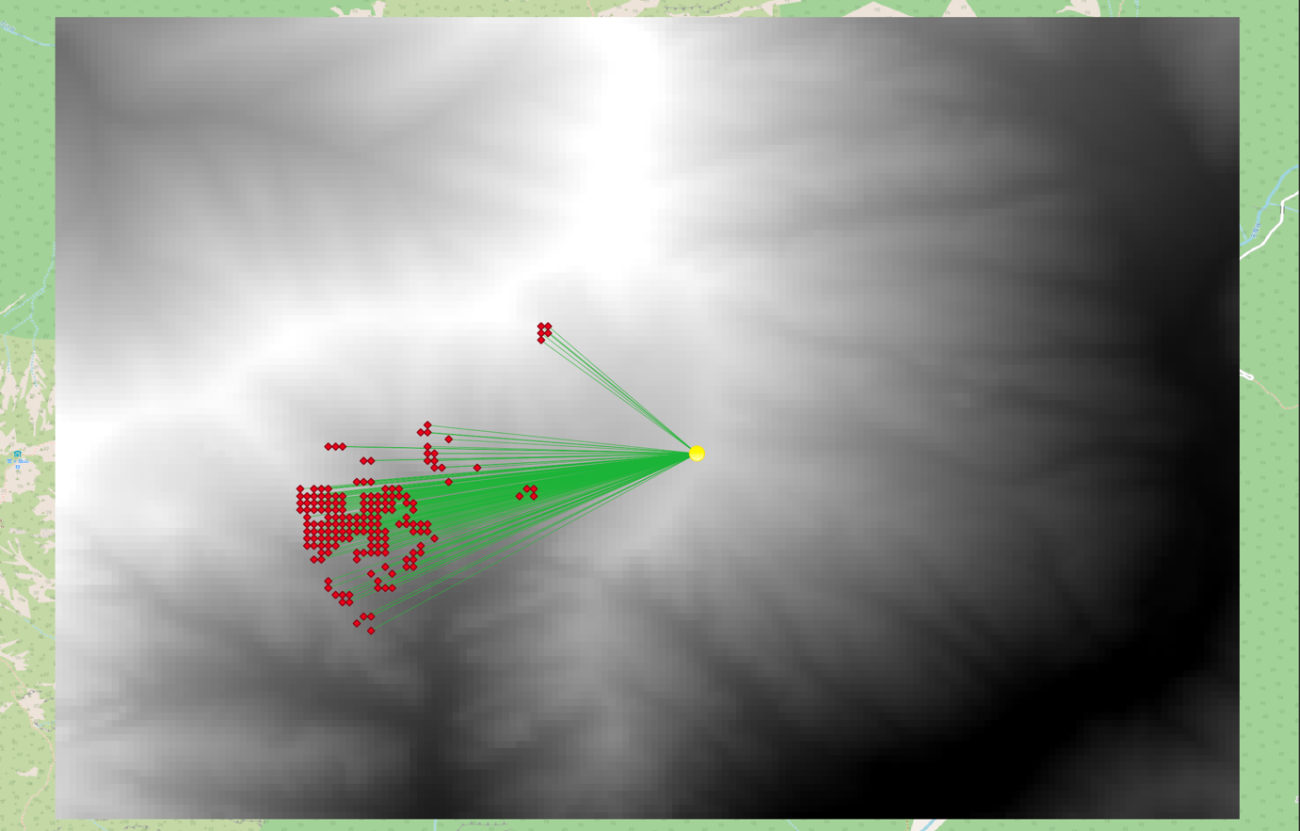
反射地点:赤色の菱形、反射経路:緑色の直線、音源:黄色の丸 Credit : JAXA, OpenStreetMap
GeoJSONで格納する時に、地物の特徴量の情報として経過秒数、クラスター、反射角度などの様々な情報を付随して管理することができます。
例えば、反射経路にやまびこの経過時間を表示すると図 24のようになります。
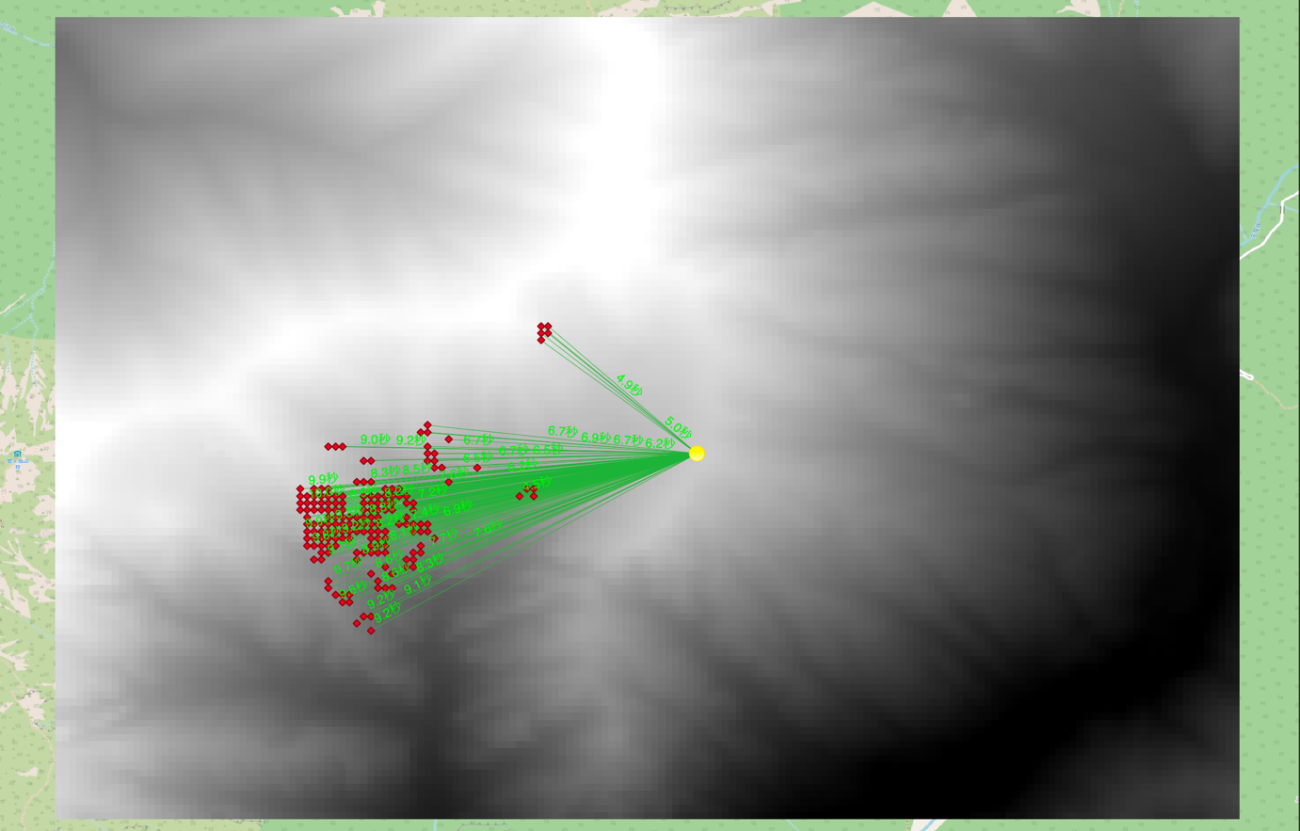
Credit : JAXA, OpenStreetMap
また、クラスター分類のクラスを表示すると、図 25のように反射地点と共に確認することができます。
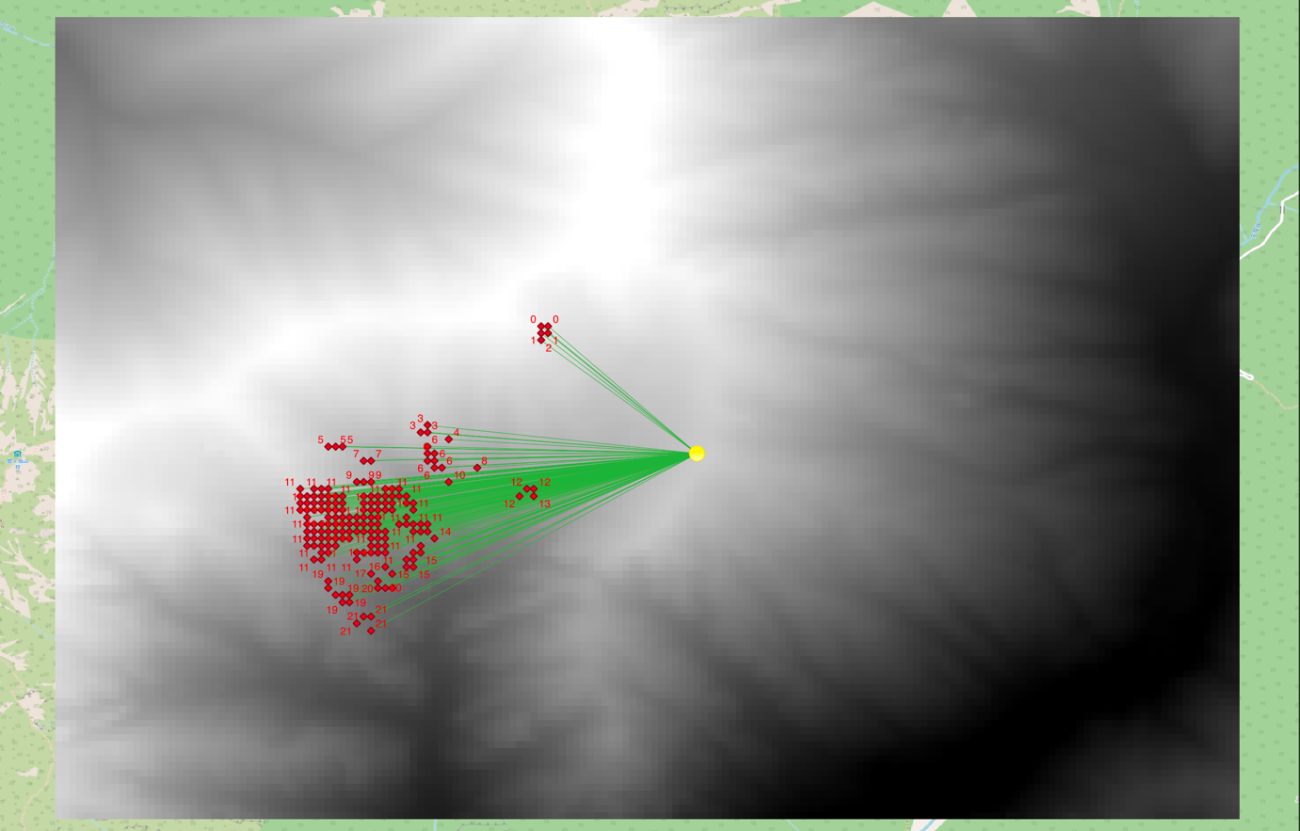
国土地理院の航空画像をベースマップにして可視化すると反射面の詳細もわかりそうです。
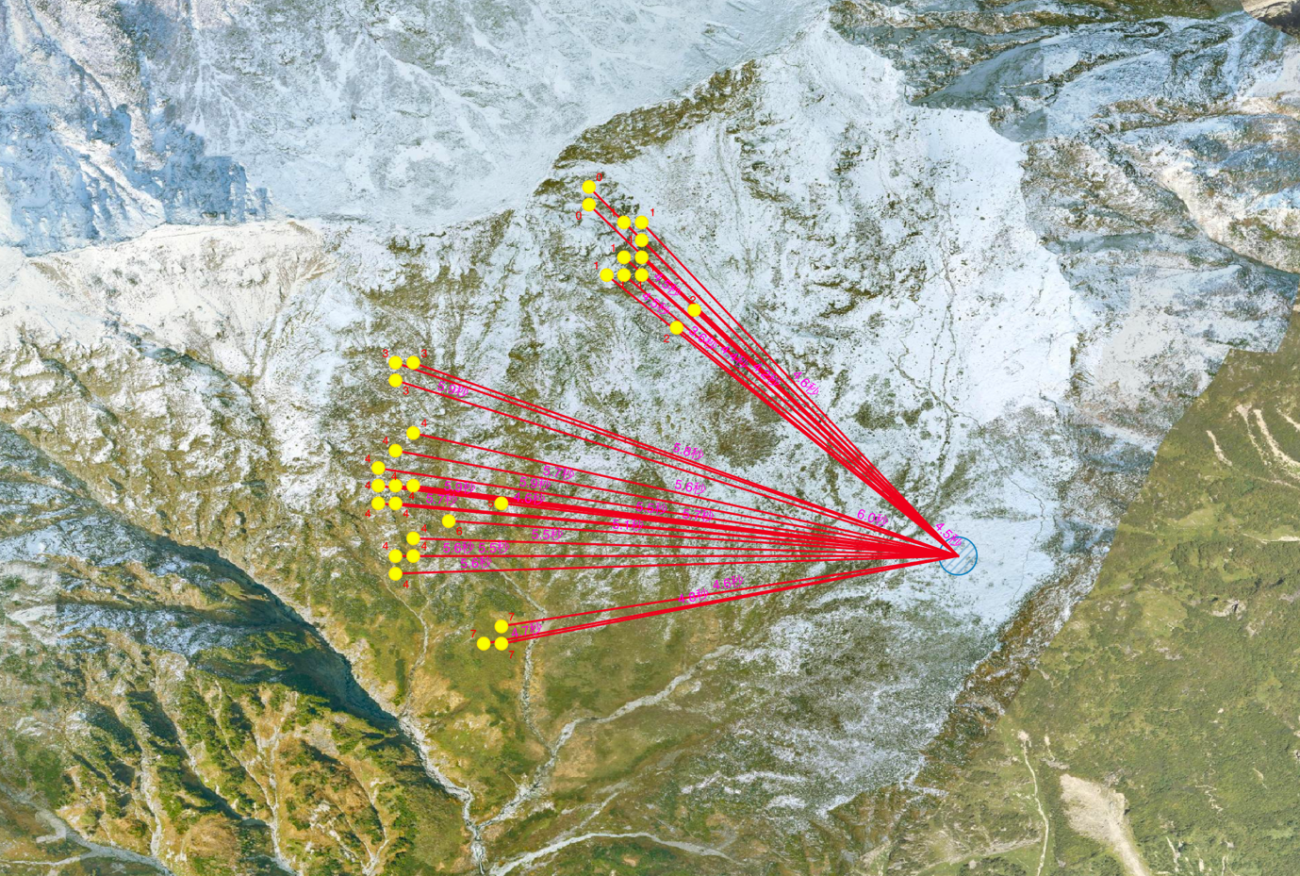
さらに、地理空間情報があることでその他の複合的なデータを融合させることが可能になります。本記事では、衛星データを利用することで現地の様子をよりリアルに把握することで、反射地点の雪や植生の空間的な状態も判断に入れてみたいと思います。
今回使用する衛星データは、ESA の Sentinel-2 という光学衛星の画像を使用します。図 27は2024年10月21日の観測画像です。直近の雲なしの画像を選定したことで、少し時間が経過しています(山岳部は晴れ間が少ないため)が、現地の状態はわかりそうです。

図 28では、赤い菱形の反射地点を少し透過して表示しています。こうすることで、衛星画像から地表面の状態を把握しやすくしています。
ざっくりとした定性的な判断ですが、図 28の赤い領域で囲まれた領域では、岩が剥き出しており良い反射面になっていると考えられます。
逆に、図28のオレンジ色で囲まれた領域では、緑が生い茂っていて植生が多いために、悪い反射面になっています。また、水色で囲まれた領域では、雪が積もっていてこちらも同様に悪い反射面になっています。
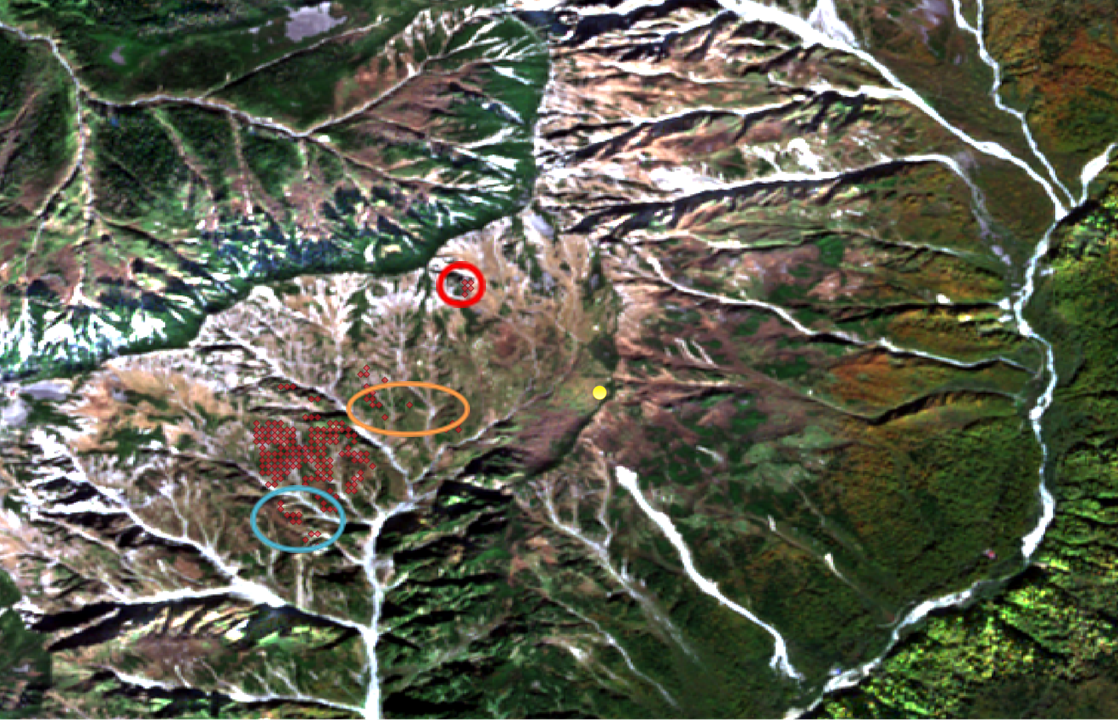
Credit : Contains modified Copernicus Sentinel data 2025 processed by Sentinel Hub
地理空間投影するメリットは他にもあります。QGISをはじめとしたGISツールの計測や処理に対応できるようになります。例えば、2点の距離を測ることで反射集団のより精密な距離も求めることができます。図29のように771mと計測できます。
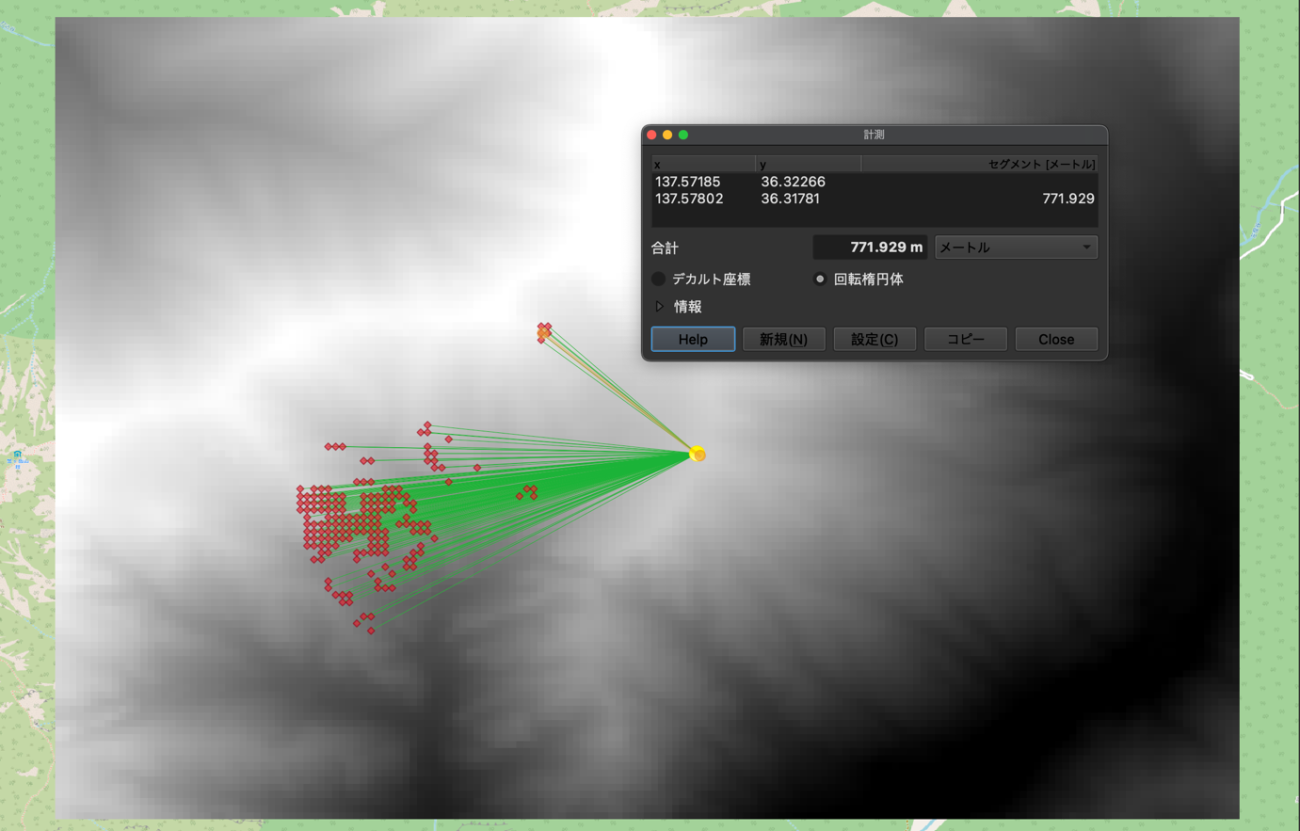
また、QGISの標高断面図ツールを使用することでやまびこの反射地点までの地形の変化を可視化することが可能です。
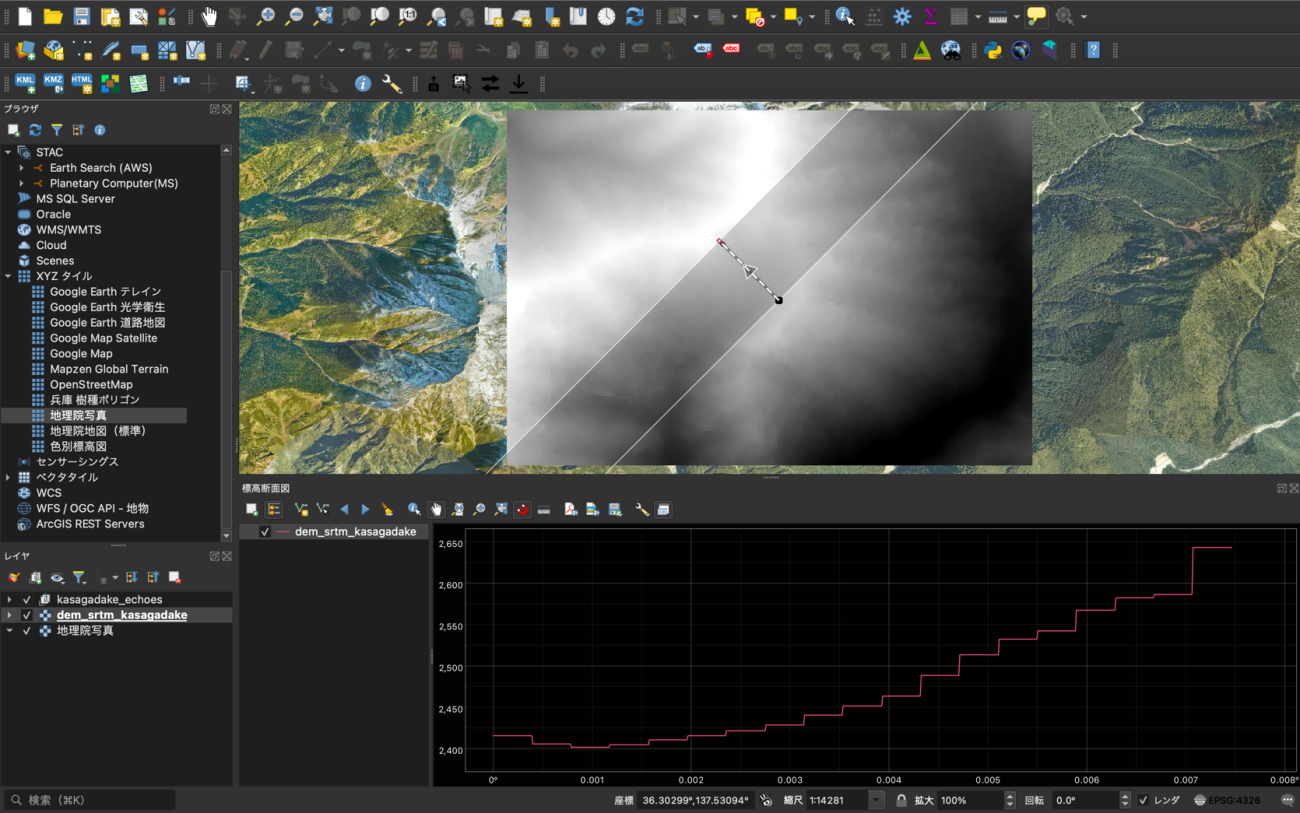
© NASA ©国土地理院
Credit : NASA, 国土地理院
断面図にすることで反射地点の場所がいきなり急な斜面になっていることがわかります。シミュレーションの妥当性や現地での様子を確認するために使用できます。

やまびこの検証
ここまででリモートセンシング技術を活用してシミュレーションや解析を行ってきました。
では、実際にやまびこが聞こえた方角や秒数から妥当なシミュレーションの条件を探索していきましょう。
ekatさんに現地の情報を伺ってみると、図 31のような状況であることがわかりました。そして、発生するのは北東で、やまびこが聞こえたのは3〜4秒くらい経過してからとのことです。このような現地での情報は大変貴重です。情報提供に感謝いたします。
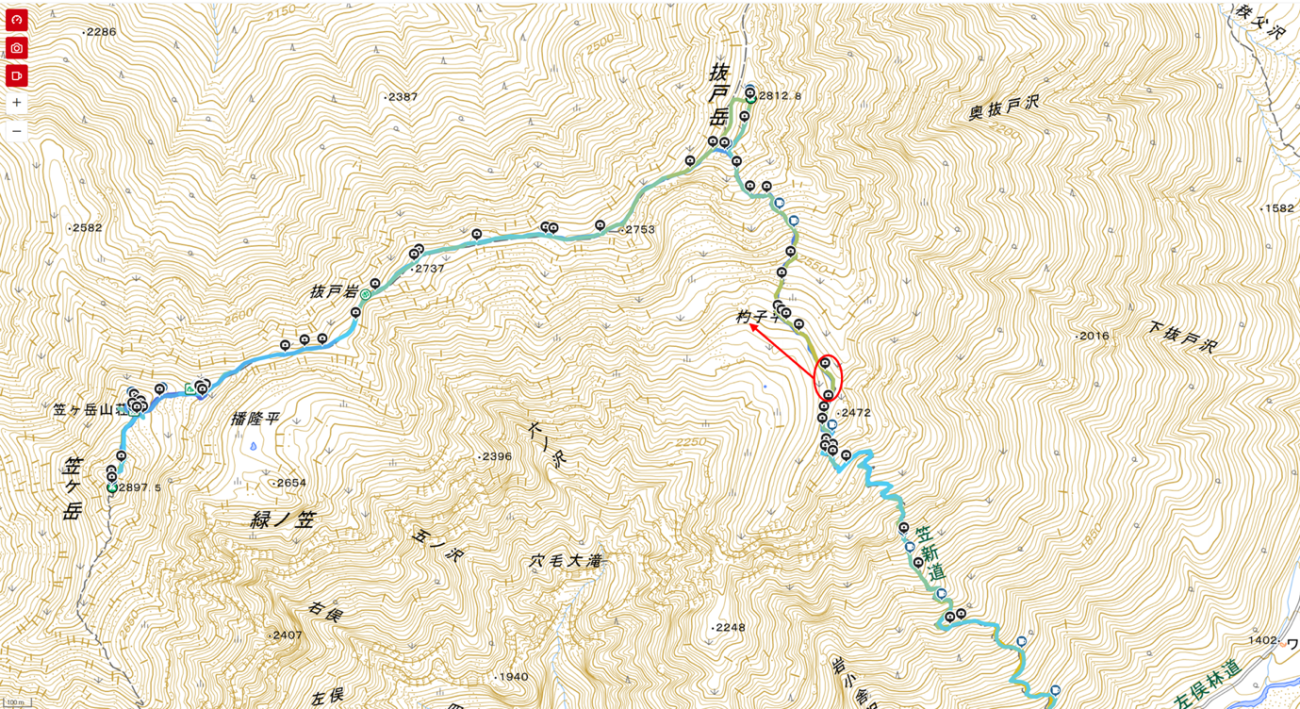
Credit : YAMAP
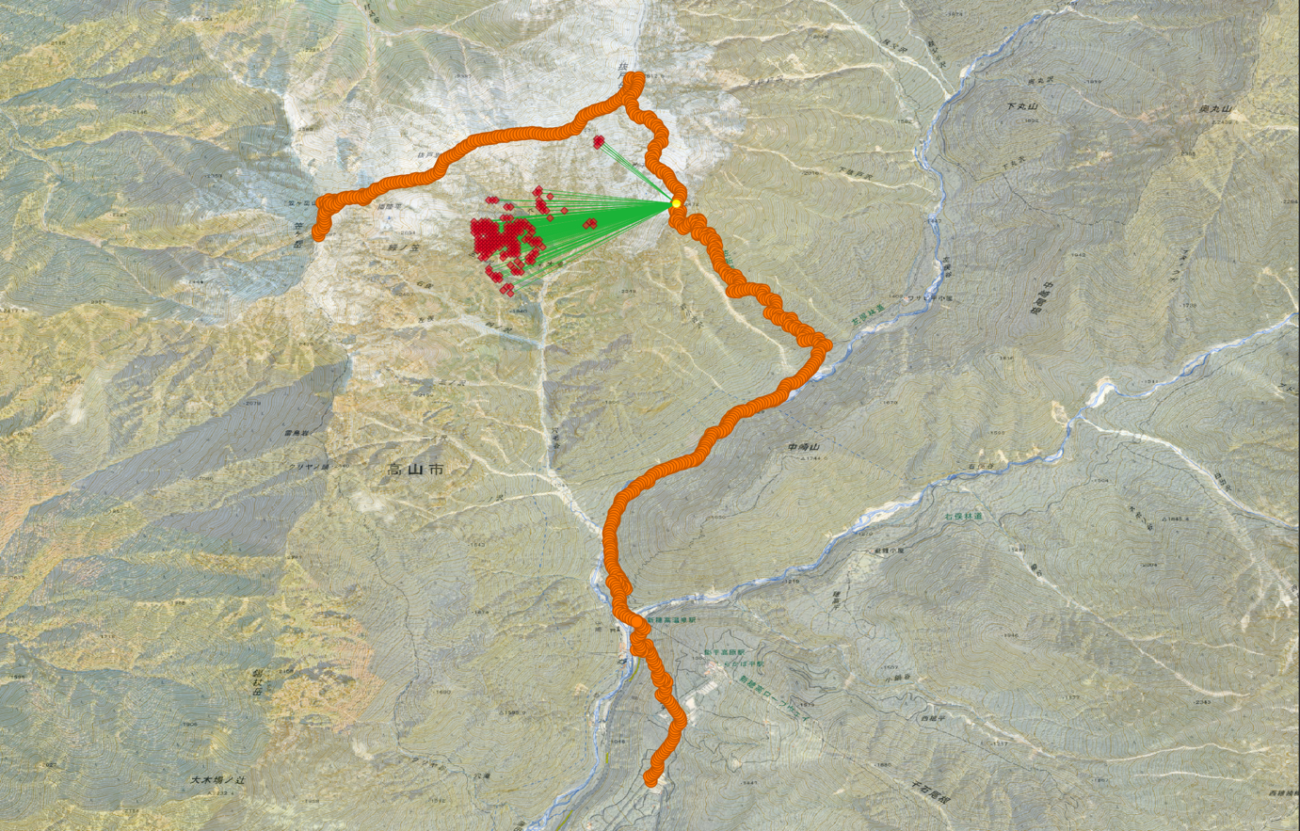
図 31と図 32からシミュレーションの結果と現地情報を比較すると、先ほど分析して図20に示した際にオレンジ色にクラスタ化された西側の反射地点は、やまびことしてはハッキリと聞こえないようです。さて、このような誤差がどこから生まれたのかを考えてみましょう。
原因はいくつか考えられます。まず1つ目は、図6の空気による音量の減衰を考慮して最大2000mの距離設定でシミュレーションする事です。2つ目は、反射面の材質の考慮です。表2のような植生や雪の考慮をすべきです。地表面がよく露出する部分に制限することで対応できそうです。
1つ目の物理シミュレーションに適応してもう一度実験してみます。
# --- シミュレーションの実行 ---
echoes, slopes = simulate_echo(
dem_data,
source_pos=(pixel_y, pixel_x),
cell_size=cell_dim,
max_distance=1000,
max_angle=85,
)
# --- 結果の表示 ---
if echoes:
print(f"\n{len(echoes)}個のやまびこの可能性を検出しました:")
# 距離が近い順にソートして表示
for echo in sorted(echoes, key=lambda x: x['distance_m']):
print(
f" - 反射位置: {echo['position']}, "
f"距離: {echo['distance_m']:.1f} m, "
f"遅延時間: {echo['delay_s']:.2f} 秒, "
f"斜面傾斜: {echo['slope_deg']:.1f}度"
)
else:
print("\nやまびこが聞こえる可能性のある地点は見つかりませんでした。")12個のやまびこの可能性を検出しました:
– 反射位置: (66, 67), 距離: 706.1 m, 遅延時間: 4.15 秒, 斜面傾斜: 41.0度
– 反射位置: (67, 67), 距離: 713.1 m, 遅延時間: 4.19 秒, 斜面傾斜: 42.0度
– 反射位置: (66, 66), 距離: 735.5 m, 遅延時間: 4.32 秒, 斜面傾斜: 42.6度
– 反射位置: (67, 65), 距離: 771.3 m, 遅延時間: 4.53 秒, 斜面傾斜: 42.5度
– 反射位置: (44, 69), 距離: 810.6 m, 遅延時間: 4.76 秒, 斜面傾斜: 42.3度
– 反射位置: (45, 68), 距離: 816.1 m, 遅延時間: 4.80 秒, 斜面傾斜: 46.1度
– 反射位置: (43, 69), 距離: 829.8 m, 遅延時間: 4.88 秒, 斜面傾斜: 41.6度
– 反射位置: (44, 68), 距離: 834.1 m, 遅延時間: 4.90 秒, 斜面傾斜: 51.3度
– 反射位置: (43, 68), 距離: 852.8 m, 遅延時間: 5.01 秒, 斜面傾斜: 47.3度
– 反射位置: (44, 67), 距離: 858.0 m, 遅延時間: 5.04 秒, 斜面傾斜: 44.7度
– 反射位置: (57, 61), 距離: 878.2 m, 遅延時間: 5.16 秒, 斜面傾斜: 41.5度
– 反射位置: (63, 59), 距離: 931.9 m, 遅延時間: 5.48 秒, 斜面傾斜: 42.4度
音波の伝搬アニメーションはこちらです。
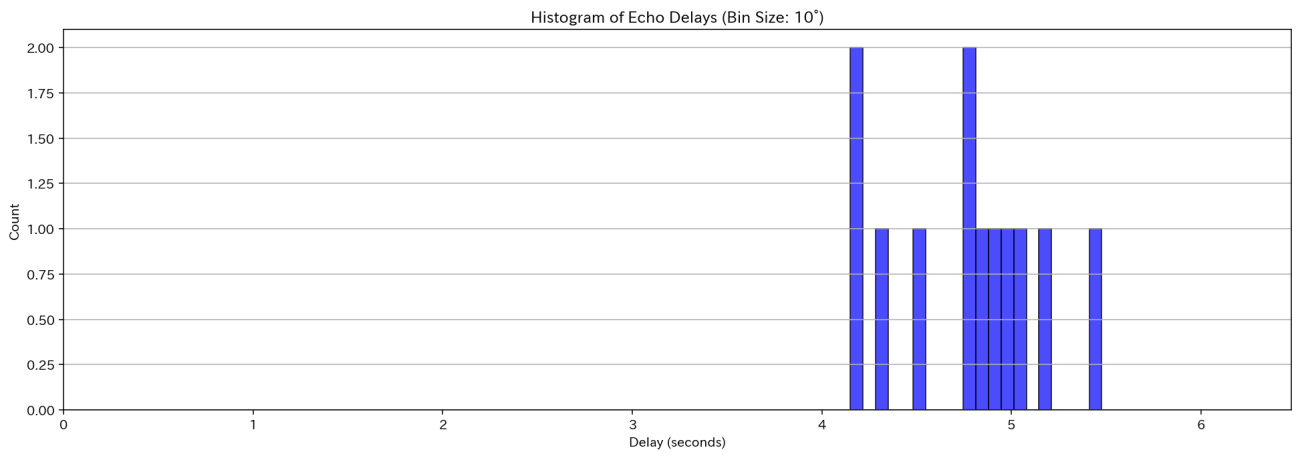
図34のように「ヤッホー」が聞こえるまでの経過時間についても近い値が出てきています。
2つ目に関して、衛星画像をHSV変換して白や緑を除くなどと処理をすることで対処できそうですが、衛星画像次第なので今回は割愛します。
検証結果から、上記の2つの改善をすることで、現地の情報と図 33のシミュレーションは似たような結果になりました。このようにして「ヤッホー」とやまびこが聞こえるヤッホーポイントを探索して特定することも可能ですね。

衛星データをはじめとした最新技術と科学を駆使することで様々な解析。そして、こめじゃらしと楽しくやまびこのシミュレーションをしました。
読者の皆様が現地に行って「ヤッホー」と叫びたくなっておりましたら幸いです。そして、やまびこスポットを発見したら、ぜひ「山の日ヤッホー選手権2025」にご参加ください。
コードは Gtihub: こちらで公開しております。
こちらの記事は4本構成を予定しています。次回は登山アプリ「YAMAP」の活動日記(山行記録)の登山ルートから、やまびこが聞こえるヤッホーポイントを探索しました。


