突然ですが、ロケットの打ち上げを生で見たことありますか？

ものすごい轟音とともに宇宙へと飛び立つその様は一生に一度は生で、近くで見ておきたいイベントのひとつと言っても過言ではないでしょう。

現在、日本国内のロケット射場は鹿児島県の内之浦、種子島と北海道大樹町の3か所。そして、2021年は和歌山県串本町にロケット射場が2021年夏に着工予定です。

実は、種子島の打ち上げも東京で確認できるスポットがあったり、皆さんの家からロケットの打ち上げが見えるかもしれません。

本記事ではロケットの打ち上げを観測できる場所を標高データを用いてマッピングしてみました。ぜひ鹿児島、和歌山でロケットの打ち上げがある際に近所で観測できるポイントがあるかを確認してみてください。
※大樹町のロケット射場については公式に見学場が定められているため、可視エリア推定を行わず、インターステラテクノロジズ社にコメントをいただきました

(1)ロケット打ち上げの可視エリア判定！ 計測方法と利用するデータ紹介

まず、今回の記事で行うロケットの打ち上げを観測できる範囲(可視エリア)の測定方法を整理してみました。

可視エリア測定は、言い換えれば、特定対象物と観測する場所の2地点間における可視・不可視判定の繰り返しです。

宙畑でも標高データを用いて「地球の丸さを考慮して、2地点間の可視性を考えてみた」「神戸の夜景は何万ドル？衛星データを使って実際に計算してみた」といった可視判定をおこなってきました。

今回も標高データを用いて、これまでの知見を活かしながら、種子島、串本町でのロケット打ち上げについて、可視エリアを確認してみました。

大樹町でのロケット打ち上げについては、既定の場所以外での見学は原則NGとなっておりますので、見学できるスポットを紹介します。

(2)鹿児島発、和歌山発、大樹町発のロケットの打ち上げを見学できる場所は？

可視エリアの推定結果を見る前に、データを確認する上での注意点をお伝えします。今回は打ち上げ場所の緯度経度から算出する標高情報をもとに可視エリアを表示しています。そのため、可視エリアとして表示する中には、立ち入ってはいけない私有地や危険な場所も存在します。ロケットの打ち上げを見に行く場合は必ずその場所が立ち入って良い場所かどうかを確認しましょう。

それではいよいよ解析結果を確認してみましょう。まず解析をしたのは種子島からの打ち上げです。

■種子島

高さ500m、半径20kmで計算した結果が以下になります。

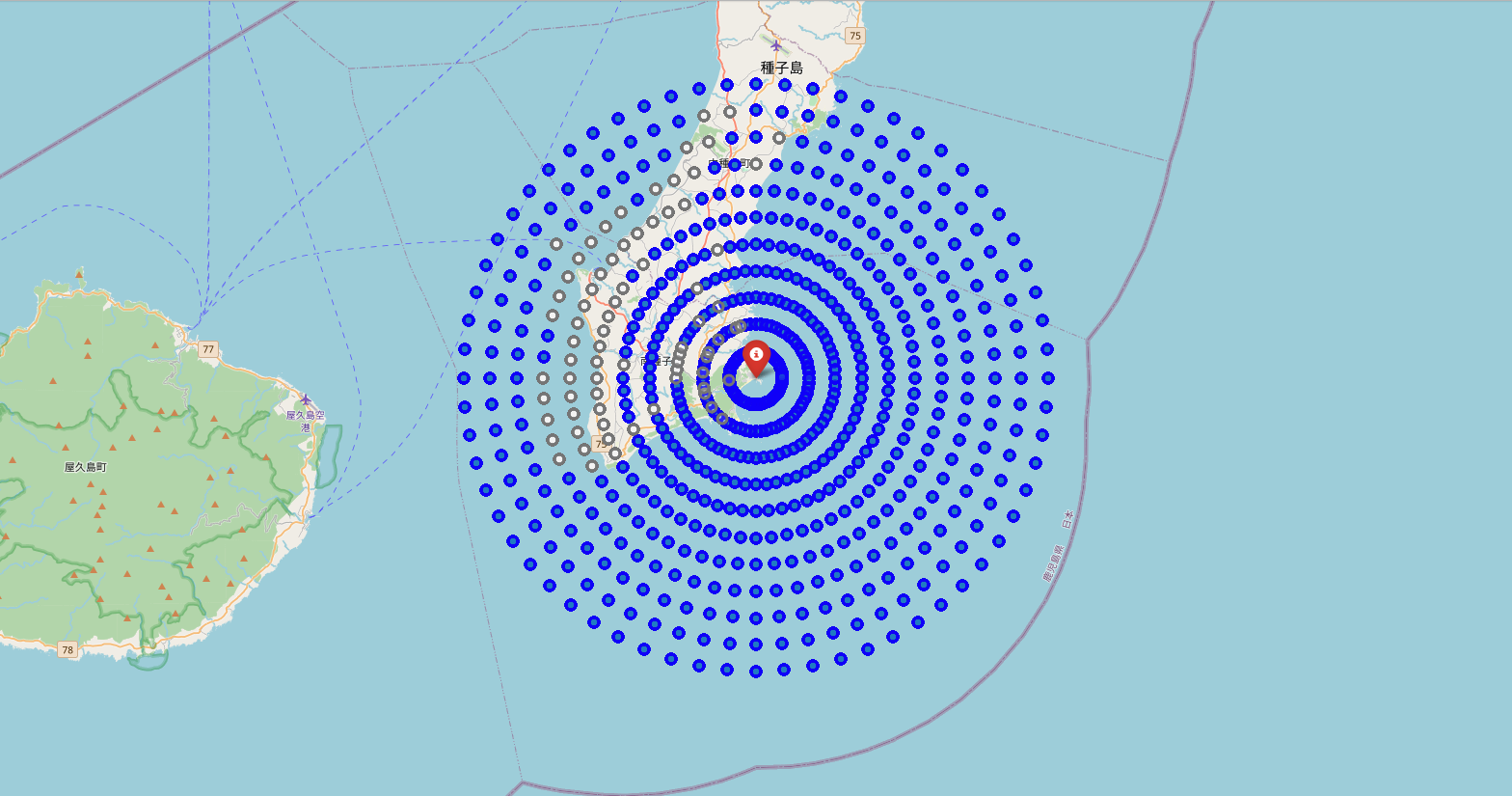
種子島の東側にロケットが見えなくなっている個所があるようですが、基本的には種子島内であれば見えるところが多いようです。

ちなみに、JAXAと南種子町役場がおすすめする4つの見学場所をプロットしてみた地図は以下のようになります。

■串本町

続いて串本町です。

高さ500m、半径20kmで計算した結果が以下になります。

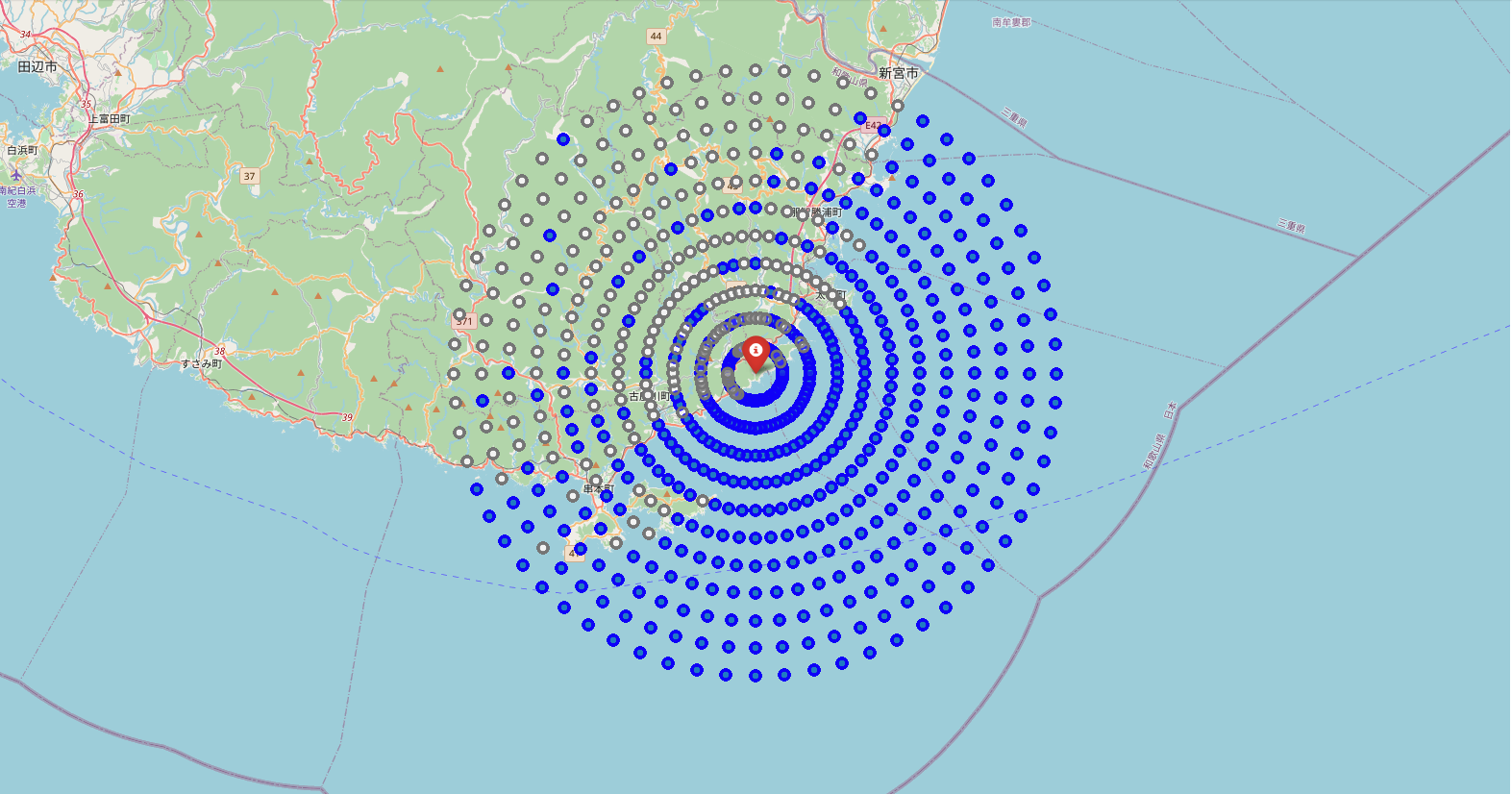
串本に新設される予定の射場は傾斜が激しい場所にあることから、観測できるスポットがまばらになっているようです。もちろん、ロケットの高さを1,000mに変更すれば観測できるスポットはさらに拡がるでしょう。

■大樹町

大樹町にて、インターステラテクノロジズ社のロケット打ち上げを見学ができる場所は公式に「SKY-HILLS」の1箇所のみとなっています。

「SKY-HILLS」について、インターステラテクノロジズ社より以下のコメントをいただきました。

SKY-HILLSはインターステラテクノロジズ社が主催するロケット打ち上げ見学場。ロケット射場（北海道スペースポート内）から約4kmの距離に位置する芝地の見学場で、町内で唯一ロケットの射点を直接眺めることができるスポットです。過去には公式グッズ販売やお子様向けのモデルロケット教室などのワークショップも行われています。

ぜひ一般開放の際は訪れてみてください。

【SKY-HILLSの場所】

(3)コード紹介

基本的な見通しの計算は、「富士山が見える場所はどこまで？標高データから解析！【Tellusでやってみた編】」の通りです。

【実行環境】
Python 3.7.3
tqdm 4.57.0
ipywidgets 7.6.3
Folium 0.12.1

0.準備

この計算をロケット発射場と同心円上の観測点との間で計算していきます。

まず必要なライブラリを追加するために、JupyterLabのターミナルを開きます。

ターミナルに下のコマンドをコピペしてEnterを押します。

cd work/ && pip install folium tqdm ipywidgets -U

1.ロケット発射場の情報を設定

発射場の場所を緯度経度で指定します。今回ロケットの軌道が分からなかったので、ロケットの高度を500mと仮定します。

lon1,lat1 = 135.89032, 33.54467 #ロケット発射場
height = 500 # ロケット打ち上げ時の高さを指定[m]
los_radius = 20 #見通しエリアの半径[km]
concentric_circle = 10 # 見通しエリアの同心円の数
accuracy = 100 # 見通し計算の精度

#発射場の緯度経度は発表資料から予測
#https://news.mynavi.jp/article/kushimoto-2/

2.2地点間の標高を取得

国土地理院のデータを使用し2地点を結ぶ直線上の標高を取得する関数を用意します。使用したデータは「地理院地図｜サーバサイドで経緯度から標高を求めるプログラム」です
※余談ですがpyprojというGISの座標計算ライブラリがめちゃくちゃ便利だったのでオススメしておきます

# 2地点間の座標を取得
from pyproj import Geod
def get_midpoints(lon1,lat1,lon2,lat2,npts=10):
    """
    2地点間の緯度経度を取得
    
    lon1,lat1 : ロケットの座標
    lon2, lat2：観測点の座標
    npts: 取得する2点間の座標の数
    """
    geod = Geod("+ellps=WGS84")
    return geod.npts(lon1, lat1, lon2, lat2, npts)

# 座標から標高を取
import requests, json
def get_kokudochiriin_elevation(lon,lat):
    """
    国土地理院の標高データを取得
    """
    url = "https://cyberjapandata2.gsi.go.jp/general/dem/scripts/getelevation.php?lon={}&lat={}&outtype=JSON".format(lon,lat)
    r = requests.get(url)
    data =json.loads(r.content)
    return data['elevation']

3.2地点間の視線を計算

三角関数に基づいて2地点間の視線を計算するための関数を用意します。

コード下部にget_shizumikomiという関数がありますが、沈み込み量については「地球の丸さを考慮して、2地点間の可視性を考えてみた」を参照ください。

def get_distance(lon1,lat1,lon2,lat2):
    """
    2点の距離を取得
    """
    grs80 = Geod(ellps='GRS80')  # GRS80楕円体
    azimuth, bkw_azimuth, distance = grs80.inv(lon1, lat1, lon2, lat2)
    return distance

import math
def get_angle(height,distance):
    """
    底辺と高さから角度（°）を取得
    """
    tan = height/distance
    return math.degrees(math.atan(tan))

def get_height(distance,angle):
    """
    底辺と角度から高さを取得
    """
    return distance * math.tan(math.radians(angle))

def getHorizonDistance(h0, earth_radius):
    if h0 < 0:
        h0 = 0
    return math.sqrt( math.pow(h0, 2) + 2 * earth_radius * h0 );

def getTargetHiddenHeight(d2, earth_radius):
    if d2 < 0:
        return 0;
    return math.sqrt(math.pow(d2, 2) + math.pow(earth_radius, 2)) - earth_radius;

def get_shizumikomi(observer_height, distance):
    """
    observer_height : 観測点の標高(m)
    earth_radius : 対象点との距離(m)
    """
    earth_radius = 8494.666 #光の屈折を踏まえた地球の半径4/3倍（ここでは光の屈折率を電磁波と同じと見なす） （実際の半径は6371km）
    
    observer_height_km = observer_height * 0.001 #地球半径の単位と合わせるため km に変換
    distance_km = distance * 0.001
    
    oberver_to_horizon_km = getHorizonDistance(observer_height_km, earth_radius);
    shizumikomi_km = getTargetHiddenHeight(distance_km - oberver_to_horizon_km, earth_radius);
    
    return shizumikomi_km * 1000; # m に直す

4.標高と視線を比較する関数を用意

上で用意した関数を使って標高と視線を比較する関数を用意します

from tqdm.notebook import tqdm

def customize_return(elevation):
    if "-----" == elevation:
        return 0
    else:
        return elevation
    
def is_los_true(lon1,lat1,lon2,lat2,height,npts):
    """
    2地点間の見通しを計算
    
    lon1,lat1 : ロケットの座標
    lon2, lat2：観測点の座標
    npts: 標高を取得する座標の数
    
    return: los_true:見通せる緯度経度、los_false:見通し不可な緯度経度
    """
    # 2地点間の座標を取得
    mid_points = get_midpoints(lon1,lat1,lon2,lat2,npts)
    
    # 観測点も追加
    mid_points.append((lon2,lat2))
    
    #観測点→対象点に近い点の順に並び替え
    mid_points.reverse()
    
    # 中間点の数を取得(観測点を含む)
    mid_points_count = len(mid_points)
            
    # 観測点から、対称点の距離を取得
    distance = get_distance(lon1,lat1,lon2,lat2)
        
    # 中間点間の距離を取得
    span = distance/mid_points_count
        
    # 観測点からの視線計算の角度を取得
    observer_elevation = customize_return(get_kokudochiriin_elevation(lon2,lat2))

    #底辺をそろえる
    height = height - observer_elevation
    
    #見た目の高さを取得
    height = height - get_shizumikomi(observer_elevation,distance)

    #角度を取得
    angle = get_angle(height,distance)
        
    for index in range(mid_points_count):
        
        #中間点を取得
        mid_point = mid_points[index]
        
        #中間点から対象点までの距離
        span_sum = span * ( index + 1 )
                
        #現在の中間点における、視線の高さを計算
        mid_los_height = get_height(span_sum,angle)
        mid_los_height = mid_los_height + observer_elevation
        
        #現在の中間点における、標高を取得
        mid_elevation = customize_return(get_kokudochiriin_elevation(mid_point[0],mid_point[1]))
        mid_elevation = mid_elevation - get_shizumikomi(observer_elevation,span_sum)
        
        # 視線と中間の標高の比較
        if mid_los_height < float(mid_elevation):
            result = False
            break;
        else:
            result = True
            
    return result

5.円周上の緯度経度を取得する関数を用意

from functools import partial
import pyproj
from shapely.ops import transform
from shapely.geometry import Point

proj_wgs84 = pyproj.Proj('+proj=longlat +datum=WGS84')

def geodesic_point_buffer(lon, lat, km):
    """
    中心点から半径 N km の円周の緯度経度を取得
    
    lon1,lat1 : 中心点の座標
    km: 半径 (kmで指定)
    return: 円周の緯度経度の座標
    """
    # Azimuthal equidistant projection
    aeqd_proj = '+proj=aeqd +lat_0={lat} +lon_0={lon} +x_0=0 +y_0=0'
    project = partial(
        pyproj.transform,
        pyproj.Proj(aeqd_proj.format(lat=lat, lon=lon)),
        proj_wgs84)
    buf = Point(0, 0).buffer(km * 1000)  # distance in metres
    return transform(project, buf).exterior.coords[:]

def get_concentric_circle_points_from_circumference(circumference_points,lon1,lat1, npts):
    """
    円周の外側の点から、同心円状に内側の点を取得
    circumference_points: 円周の外側の点 （lon,lat）
    lon1,lat1 : 中心点の座標
    npts : 同心円の数
    return: 同心円状の点の緯度軽度 [[(lon,lat),(lon,lat)...],[(lon,lat),(lon,lat)...]]
    """
    
    concentric_circle_points = []
        
    for circumference_point in circumference_points:
        #円周の内側の点を取得
        inner_points = get_midpoints(lon1,lat1,circumference_point[0],circumference_point[1],npts)
        #円周の外側の点も追加
        inner_points.append((circumference_point[0],circumference_point[1]))
        # 円周の特定の角度の外側から中心までの点を、配列に追加
        concentric_circle_points.append(inner_points)
        
    return concentric_circle_points

6.用意した関数を使って見通しを計算

2~5で用意した関数を使って見通しを計算、結果を地図にマッピングしていきます。
JupyterLab上でロケットを見れる地点が青、見れない地点が灰色の点で表示されます。

計算が完了すると、result.geojsonというファイルが出力されますので任意の地図で結果を
表示できます。

# pip install folium するのを忘れずに!
import folium
import collections as cl
import json

def get_los_area(lon1,lat1,height,rad_km, con_circle, accuracy):
    
    #対象点を中心とした円周上の外側の点の座標を取得
    search_areas_outer_points = geodesic_point_buffer(lon1, lat1, rad_km)#半径をkmで指定
    
    #対象点を中心とした同心円状の点の座標を取得
    concentric_circle_points = get_concentric_circle_points_from_circumference(search_areas_outer_points,lon1,lat1,con_circle)#同心円の数を指定
    
    concentric_circle_los = []
    points_true = []
    points_false = []        

    for i in tqdm(range(len(concentric_circle_points)), desc='見通しエリアを計算', leave=False):
        
        concentric_circle_point = concentric_circle_points[i]
        
        progress_radian = i * 5.45
        
        # ある角度の座標一覧を外側から見通し計算していく
        for point in tqdm(concentric_circle_point, desc='{}°上の直線の見通しを計算'.format(progress_radian)):

            result = is_los_true(lon1,lat1,point[0],point[1],height,accuracy)#中間ポイントの細かさを指定
            
            if result:
                points_true.append(point)
            else:
                points_false.append(point)
                
        concentric_circle_los.append({'los_true':points_true,'los_false':points_false})
        
    return concentric_circle_los
        
def draw_los_maker(lon1,lat1,height,rad_km,con_circle,accuracy,los_map):
    """
    見通しマーカーを地図上に描画
    """
    
    areas = get_los_area(lon1,lat1,height,rad_km,con_circle,accuracy)
    
    # GeoJSONの FeatureCollection と featuresを用意
    ys = cl.OrderedDict()
    ys["type"] = "FeatureCollection"
    ys["features"] = []
                
    # 同心円上の座標を処理
    for area in tqdm(areas, desc='見通しマップを描画'):        
        for key in area:
                        
            for points in area[key]:
                
                # GeoJSONの Feature を用意
                data = cl.OrderedDict()
                data["type"] = "Feature"
                
                # 計算結果をマーカーのカラーに反映
                if 'los_true' == key:
                    color='blue';
                    fill_color='#3186cc'
                    
                    # GeoJSONの LOS:True のプロパティを追加
                    data["properties"] = {
                        "Name":"Los:True",
                        "marker-color":"rgba(0, 0, 255, 1)",
                    }
                else:
                    color='gray'
                    fill_color='#f5f5f5'
                    
                    # GeoJSONの LOS:False のプロパティを追加
                    data["properties"] = {
                        "Name":"Los:False",
                        "marker-color":"rgba(128,128,128, 1)",
                    }
                    
                #観測点のマーカーを追加
                folium.CircleMarker(
                    location=[points[1],points[0]],
                    radius=5,
                    color=color,
                    fill=True,
                    fill_color=fill_color,
                    popup='{},{}'.format(points[0],points[1])
                ).add_to(los_map)
                
                # GeoJSON: 緯度経度を追加。
                data["geometry"] = {"type":"Point","coordinates":points}
                ys["features"].append(data)
                

    #ロケットのマーカーを追加
    folium.Marker(
        location=[lat1, lon1],
        icon=folium.Icon(color='red',icon="info-sign"),
        popup='ロケット：{},{}'.format(lat1,lon1)
    ).add_to(los_map)
        
    # GeoJSONを書き出し
    fw = open('result.geojson','w')
    json.dump(ys,fw,indent=4)


# #マップ作成
los_map = folium.Map(location=[lat1,lon1],zoom_start=13) 

# #発射場の標高を追加
height = height + get_kokudochiriin_elevation(lon1,lat1)

#見通しマーカー追加
draw_los_maker(lon1,lat1,height,los_radius,concentric_circle,accuracy,los_map)

# #地図を描画
los_map

以上、ロケット打ち上げの可視エリアを推定するコードを紹介しました。本記事に出てくるコードはgithubでも公開しています。

(4)まとめ

ロケットの可視エリア判定の検証結果とそのコードを紹介しました。ロケットの打ち上げは当たり前ですが日本一の電波塔であるスカイツリーよりも高く、宇宙まで飛び立つので、計算する高度と緯度経度によっては自分の家からも見えるという方もいらっしゃるでしょう。

本記事で紹介したコードを応用すれば、特定の対象物の可視エリアを求めることが可能になりますので、ぜひいろいろご自分の手で試してみてください。