これまで2回にわたって、人工衛星の軌道についてご紹介してきました。
最後となる本記事では、実際によく使われる軌道の種類について、いくつかご紹介をしてきます。

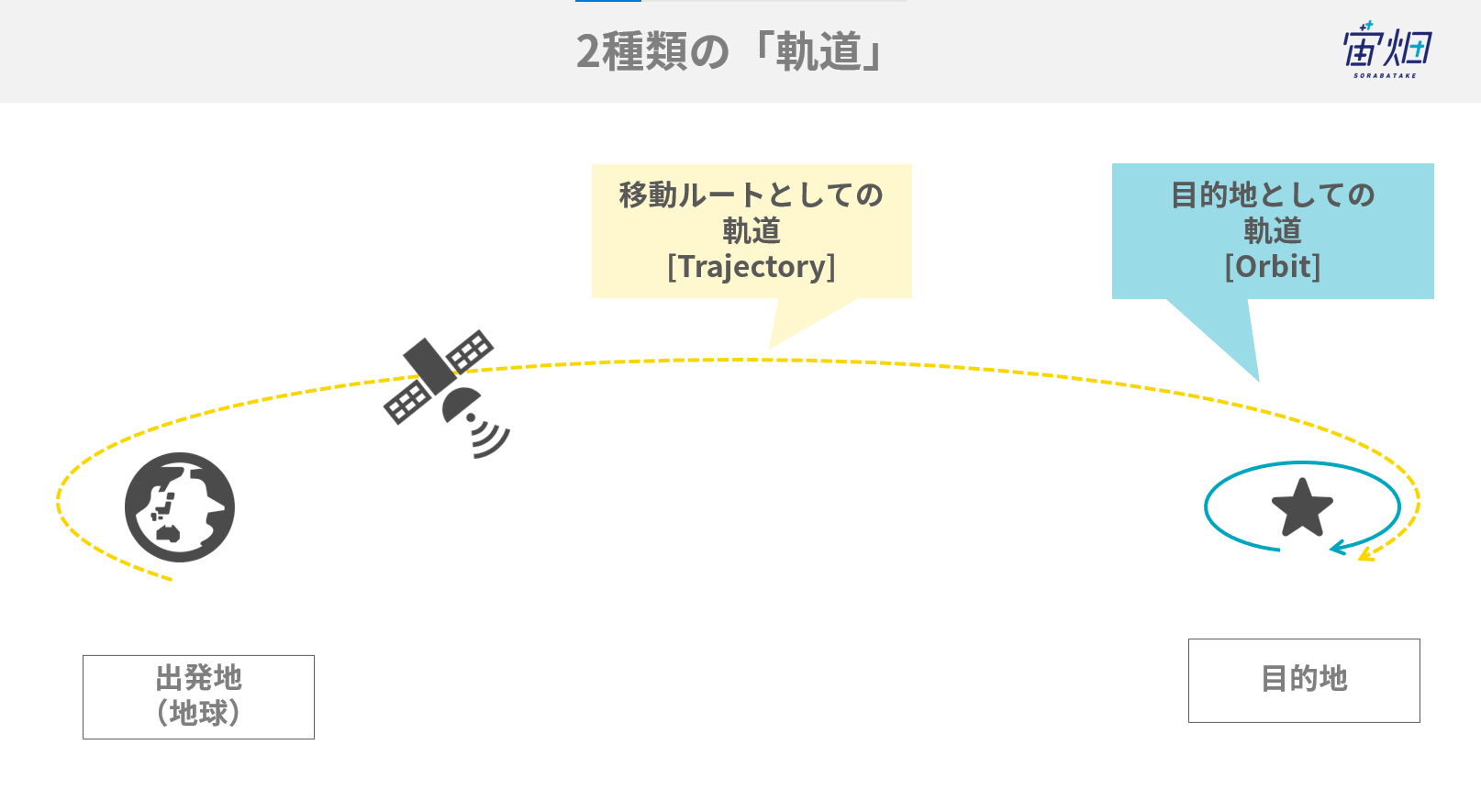
本記事では、まず「目的地」としての「軌道(Orbit)」の紹介をし、その後に「移動ルート」としての「軌道(Trajectory)」の話をしていきます。

目的地としての軌道

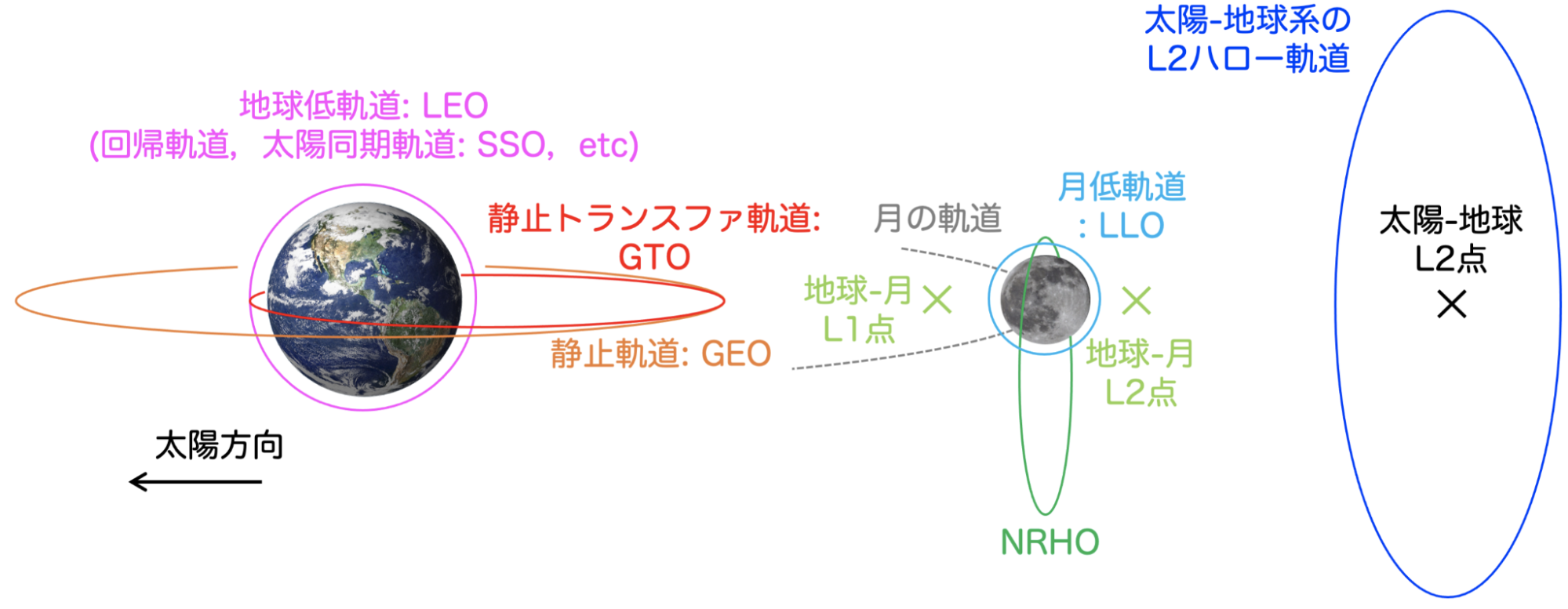
衛星のミッションによって様々な軌道がある。

冒頭でも説明したとおり、どのような軌道が採用されるかは、どのようなミッション（地球観測、通信、測位等）をしたいかどうかに大きく依存します。

例えば、地球観測衛星であれば、（同じ太陽入射条件で観測できることが重要であることが多いため）毎日何時何分JSTに日本上空を通過したいというような要求があります。

そのような要求を満たすためには、特定の軌道（この後紹介する、太陽同期準回帰軌道など）を目的地として選ぶ必要があります。ここでは、目的地としての軌道を図鑑的に紹介していきます。

地球低軌道（Low Earth Orbit: LEO）

現在最も多くの衛星が打ち上げられているのが、地球低軌道(LEO)です。一般的に地表から高度2000km以下の高度を周回する軌道を指します。高度に応じて、中軌道・高軌道という分類もありますが、地球観測等の観点から最も多く用いられるのが低軌道です。

国際宇宙ステーション(International Space Station: ISS)も、LEOを周回しています。LEOの中でも特に人気のある軌道が「回帰軌道」や「太陽同期軌道」です。

回帰軌道(Repeat Ground Track Orbit)・準回帰軌道

「回帰軌道(Repeat Ground Track Orbit)」とは、地球が自転で１周する間に、人工衛星がちょうどN周(Nは整数)する軌道です。ある日、ある地点の上空を通過した衛星は、１日後も同じ地点の上空を通過することができるような軌道です。

回帰軌道の仲間として「準回帰軌道」という軌道も存在します。これは、地球が自転でM周(Mは整数)する間に、人工衛星がN周するような軌道です。毎日同じ地点の上空は通過できませんが、M日おきに同じ地点の上空を通過することができます。

これらの軌道は、定期的に同じ地点の上空を通過してくれるため、地球観測・通信等の幅広いミッションで人気が高い軌道です。

太陽同期軌道(Sun-Synchronous Orbit: SSO)

もう一つ，人気の高い軌道が「太陽同期軌道(Sun-Synchronous Orbit: SSO)」です。「太陽同期軌道」とは、衛星の軌道面と太陽の幾何学的関係が１年を通して同じ条件になるような軌道のことです。原理については本稿では割愛しますが、地球が真球ではなく、少し潰れた楕円体である影響を活かした軌道になっています。

１年を通して衛星の軌道面と太陽の幾何学的関係が変わらないので、ほぼ同じ日の当たり方で地球観測ができるような軌道になります。

太陽同期軌道のもう一つのメリットは、衛星が経験する日陰時間（地球の影に衛星が入ってしまう時間）が年中変わらないというメリットがあります。

上手い太陽同期軌道を選べば、全日照の軌道（全く地球の影に入らない軌道）も選ぶことができ、ドーンダスク軌道（Dawn-Dusk軌道。Dawn=夜明け、Dusk=夕暮れという意味。）と呼ばれています。

衛星に常に太陽光が当たり続けるため、衛星の電力や熱設計の観点でも有利な軌道であり、地球観測衛星の中では電力を多く必要とするSAR衛星でよく選択されています。

SSOかつ回帰・準回帰軌道という軌道も存在し、LEOミッションにとって最も人気の高い軌道となっています。

また、地球周回以外でも月低軌道(Low Lunar Orbit: LLO)・火星低軌道も月・火星ミッションを行う際には、広く利用されています。これらの軌道で、地球周回のように実用的な回帰軌道・SSOが設定できるかは、天体の自転周期や重力の特性に依存します。

静止軌道（Geo Stationary Orbit = Geosynchronous Equatorial Orbit: GEO）

通信・気象観測等の宇宙利用ミッションにおいて、人気の高い軌道が「静止軌道(Geosynchronous Equatorial Orbit: GEO)」です。

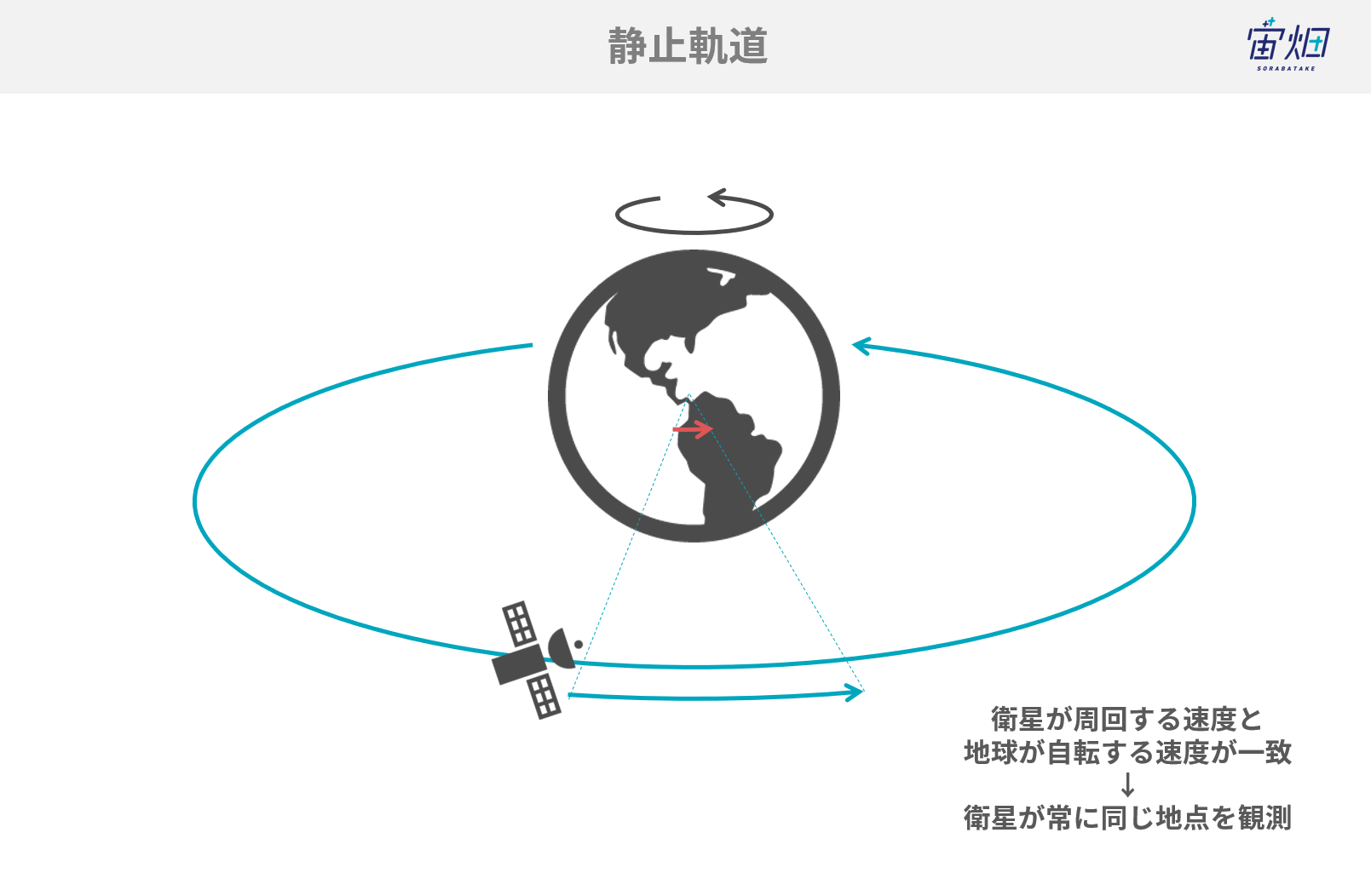
静止軌道は、地表から高度35,786kmで軌道傾斜角が0（赤道上空）の円軌道です。GEOでは衛星の公転周期と、地球の自転周期が一致しています。そのため、衛星は常に同じ地点の上空に止まり続けることができるのです。

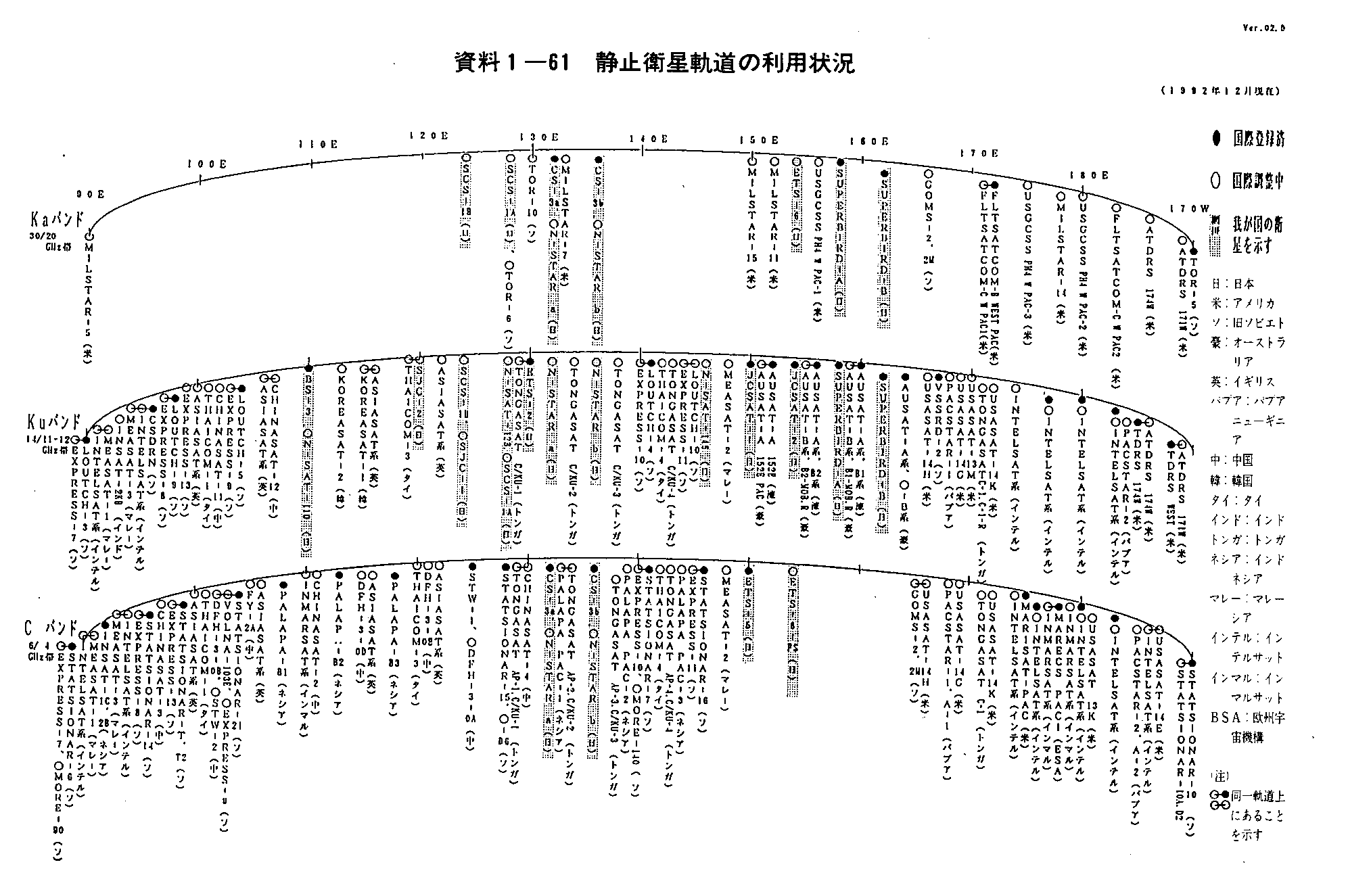
静止軌道は、24時間自国上空をモニタしたい気象観測・通信ミッション等幅広い分野で人気が高い軌道で、数多くの衛星が配置されています。

GEOに投入できる衛星の数は限りがあるため、（そもそも高度が高いのでアクセス性が悪いことも含めて）低軌道の衛星と比べて、多機能・長寿命な大型衛星が主流となっています。

対地同期軌道(Geosynchronous Orbit: GSO)・準天頂軌道

GEOは「対地同期軌道(Geosynchronous Orbit: GSO)」の一種です。

GSOでは、衛星の公転周期と地球の自転周期が一致しているのみであり、軌道傾斜角・軌道離心率に関する制約はありません。

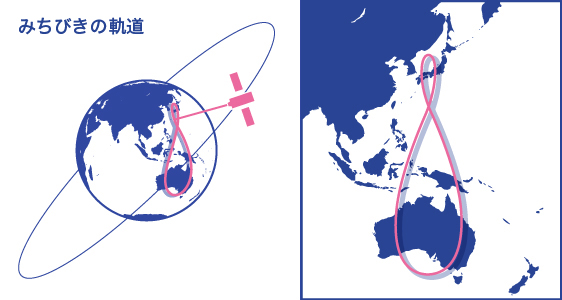
GSOでは、ある地点の上空に止まり続けることができるわけではありませんが、ある地点の上空近傍に止まり続けることができます。準天頂衛星「みちびき」が配備されている準天頂軌道は、このGSOの一種となります。
測位衛星は、測位精度を向上するために測位したい地点の天球上にまんべくなく衛星を配置することが良いとされています。準天頂軌道を選ぶことで、日本上空に定在させながら、日本上空に衛星がまんべくなく配置することを実現しています。

ハロー軌道（Halo Orbit）

地球周回から離れた月以遠のミッションで用いられる軌道も紹介します。

現在、月軌道ゲートウェイ(Lunar Orbital Platform-Gateway: LOP-G)の開発やNASAのアルテミス計画等で、月以遠ミッションが加速しようとしています。宇宙ビジネスの舞台も、地球周回軌道から月以遠へと少しずつ移ろうとしているのです。

その拠点となる月軌道ゲートウェイが配置されてようとしているのがNRHO(Near Rectilinear Halo Orbit)です。NRHOというのは、「ラグランジュ点」を基準とした「ハロー軌道」の一種なので、まず「ラグランジュ点」と「ハロー軌道」について説明をしていきます。

ラグランジュ点

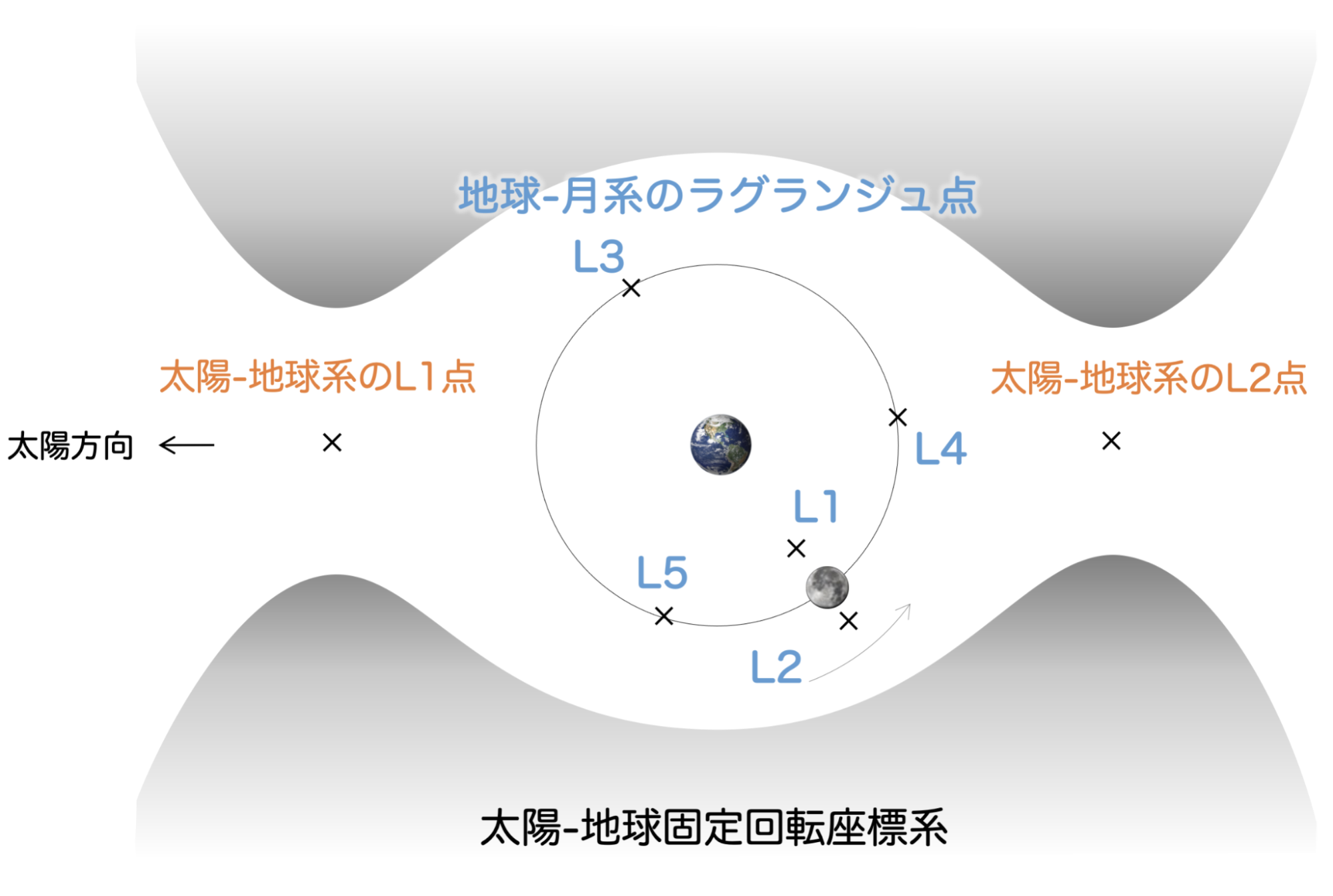
ラグランジュ点とは、三体問題※（太陽・地球・宇宙機，地球・月・宇宙機 etc…）に存在する力学的な平衡点（力が釣り合う点）を表します。

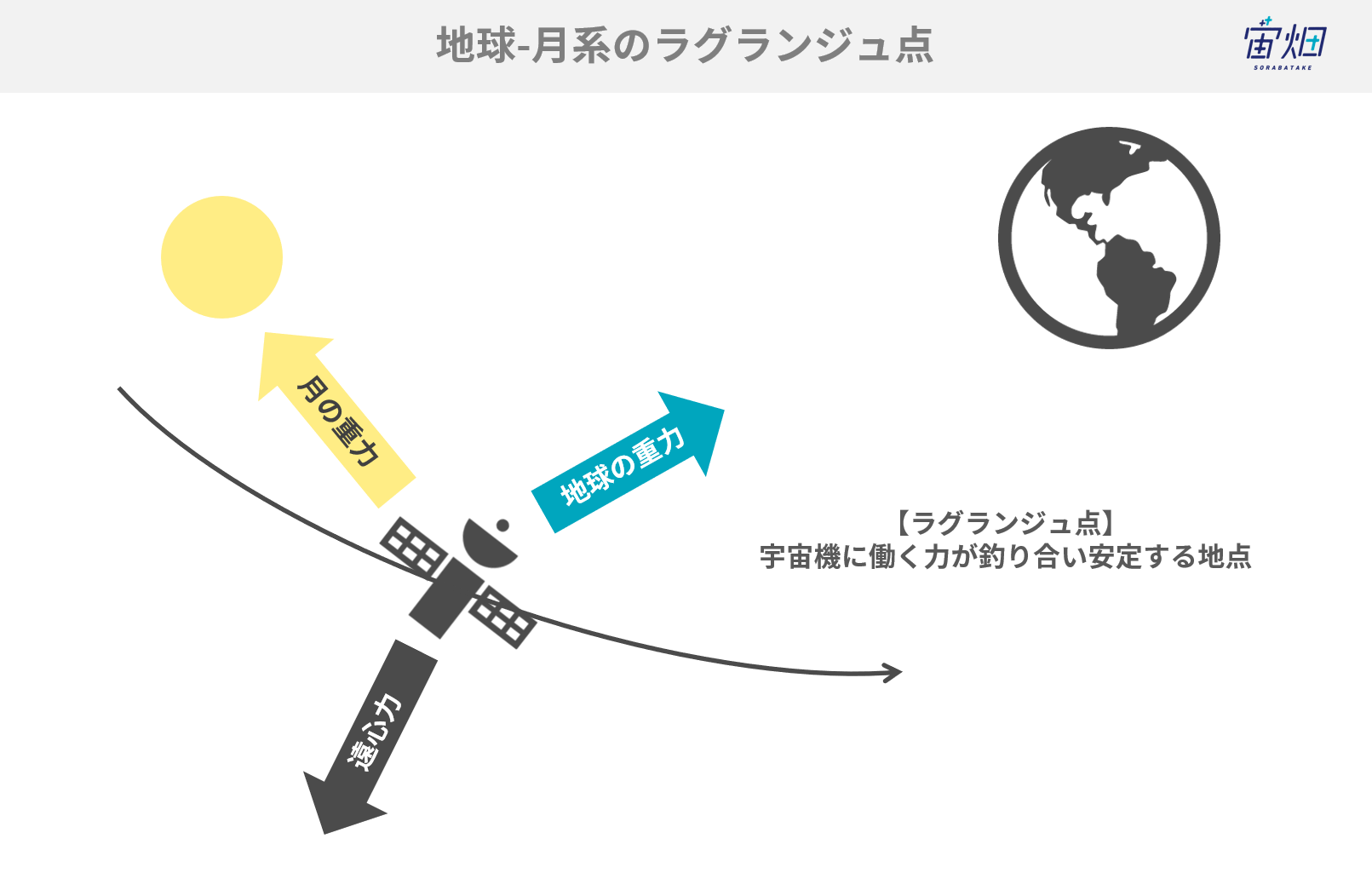
例えば、地球-月系のラグランジュ点では、地球が宇宙機に及ぼす重力、月が宇宙機に及ぼす重力、遠心力という力学的に働く力が釣り合っています。

力が釣り合う点は複数点存在するため、ラグランジュ（Lagrange）の頭文字Lを取って、L1点、L2点、L3点、、、と呼ばれます。

特に太陽-地球系のL1、L2点は、太陽と地球の幾何学的関係性が固定されるため、太陽観測（定常的に太陽を観測したい）や天文衛星（定常的に太陽光による熱から望遠鏡を守りながら観測したい）を中心とした宇宙ミッションで用いられることが多いです。また、例えば地球-月系のL2点は、地球や月へのアクセス性が高く、地球に対する月の裏側と通信ができ、更に太陽重力の影響を効果的に使うことで効率的に惑星間へ脱出できることから、月軌道ゲートウェイの建設候補地点として選ばれています。

※正確には、円制限三体問題という円軌道仮定（第一天体の周りを第二天体が円軌道で周回する）と制限仮定（宇宙機等の第三天体が他の天体に及ぼす重力が無視できる）の２つの仮定が成り立つ三体問題です。

ハロー軌道

ラグランジュ点はあくまで平衡点なので宇宙機を配置する場合は、そのラグランジュ点近傍の周期軌道に配置することになります。

ラグランジュ点近傍の周期軌道は、複数種類存在しますが最も有名なものがハロー軌道と呼ばれる軌道です。

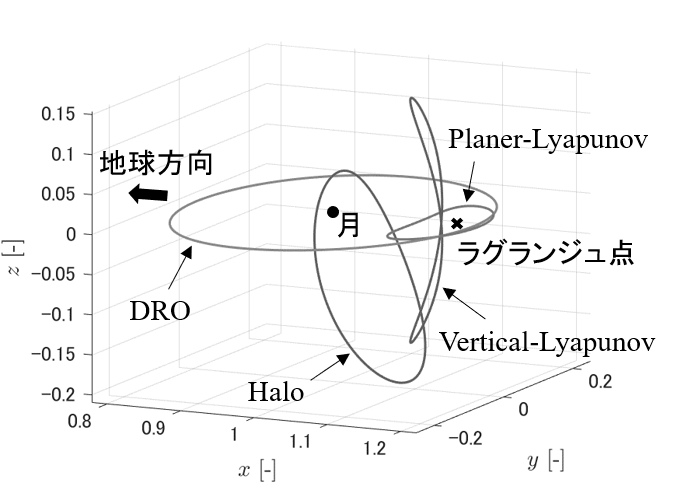
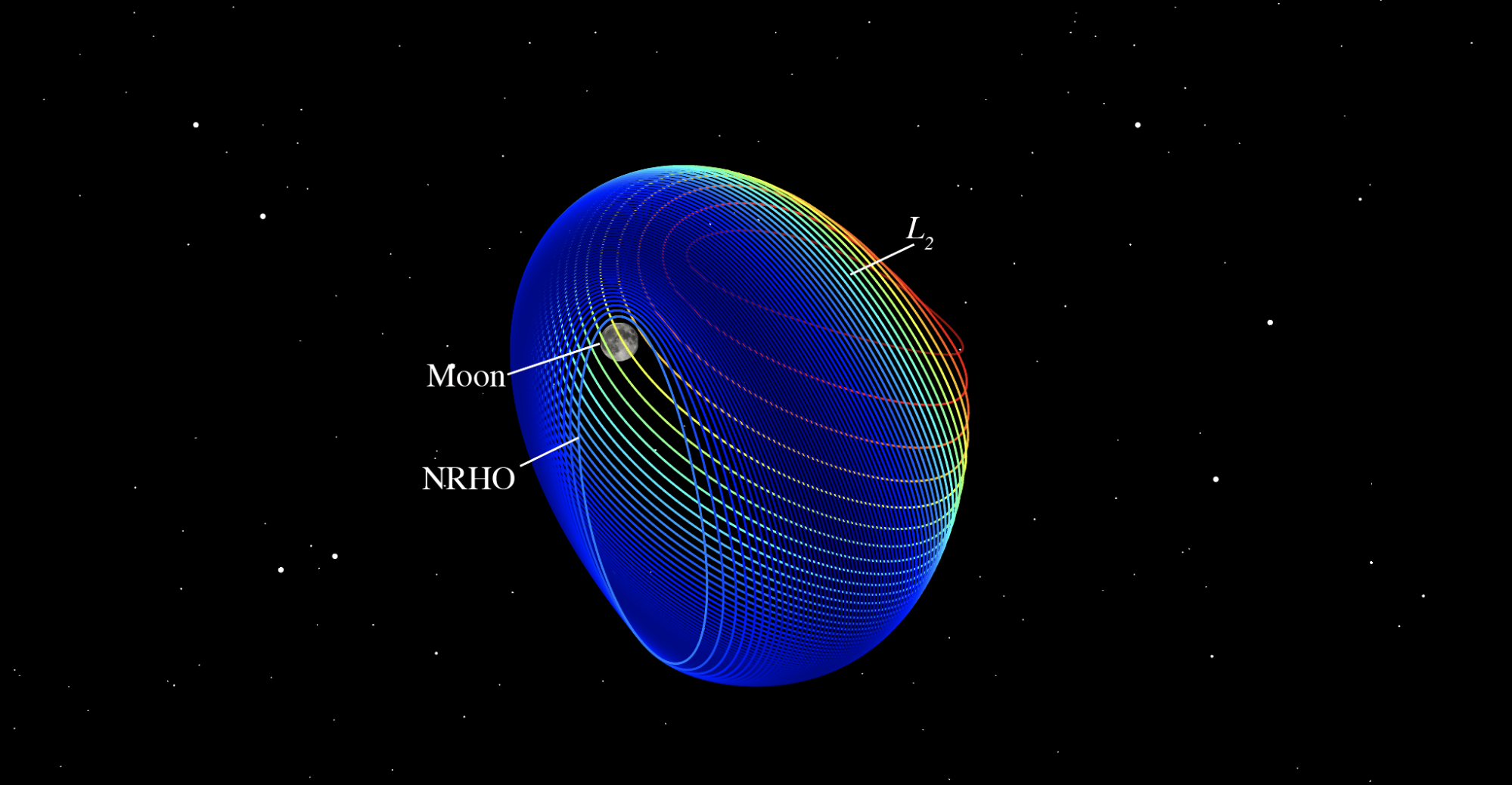
軌道のもつエネルギーごとに連続的にハロー軌道が存在し、そのハロー軌道の中で月近傍を通過する長楕円軌道に近いハロー軌道をNear Rectilinear Halo Orbit (NRHO)と呼びます。

現在開発が進行中の月軌道ゲートウェイは、地球-月系L2点のNRHOに配置される予定です。

移動ルートとしての軌道

ここまで目的地としての軌道について説明をしてきました。ここからは目的地に向かうための「移動ルートとしての軌道」の話をしていきます。

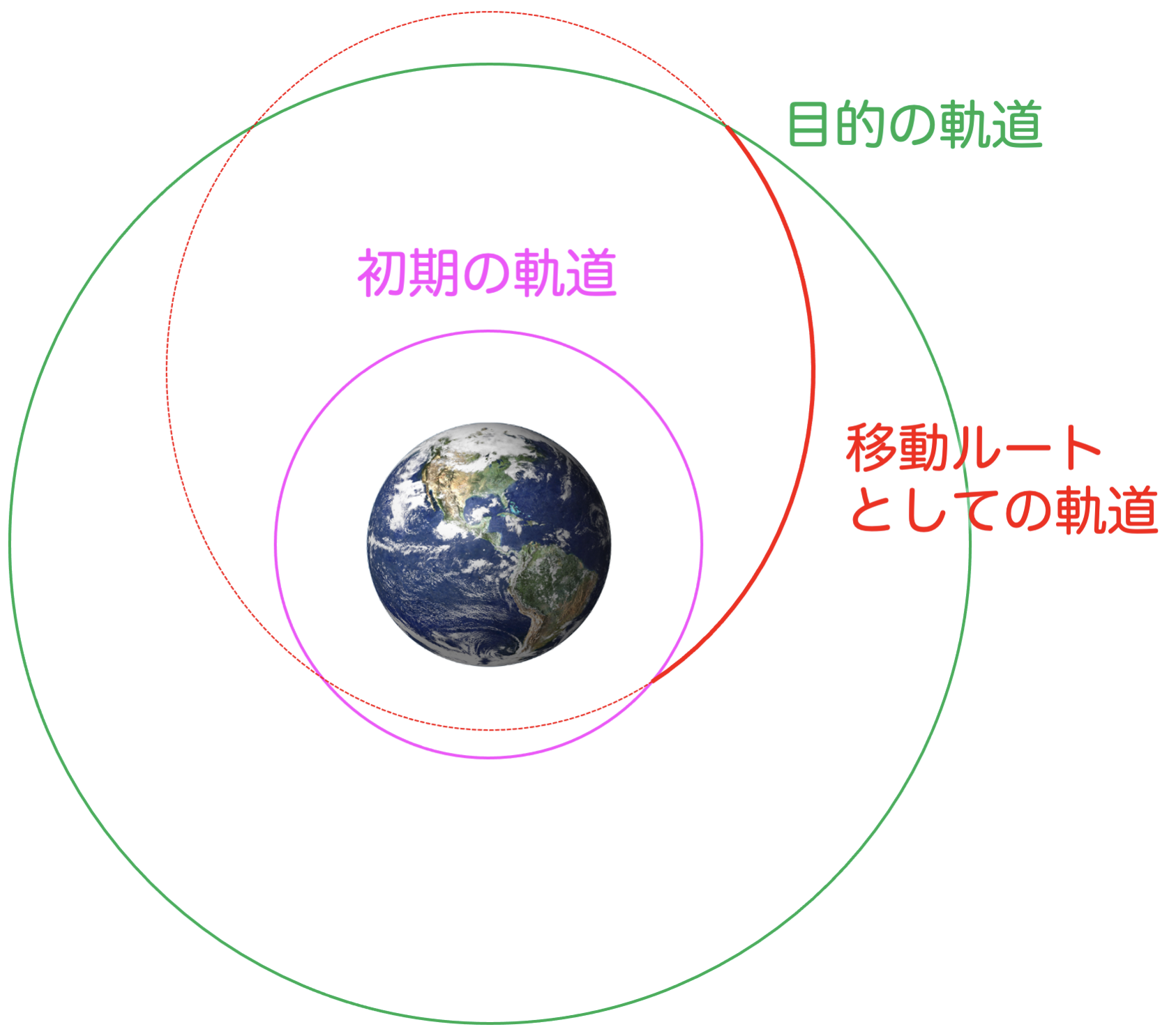
ある初期の軌道から目的の軌道に向かうためには、その２種類の軌道両方と交わる（＝位置が一致する）ような軌道を移動ルートとして選べば良いということになります。

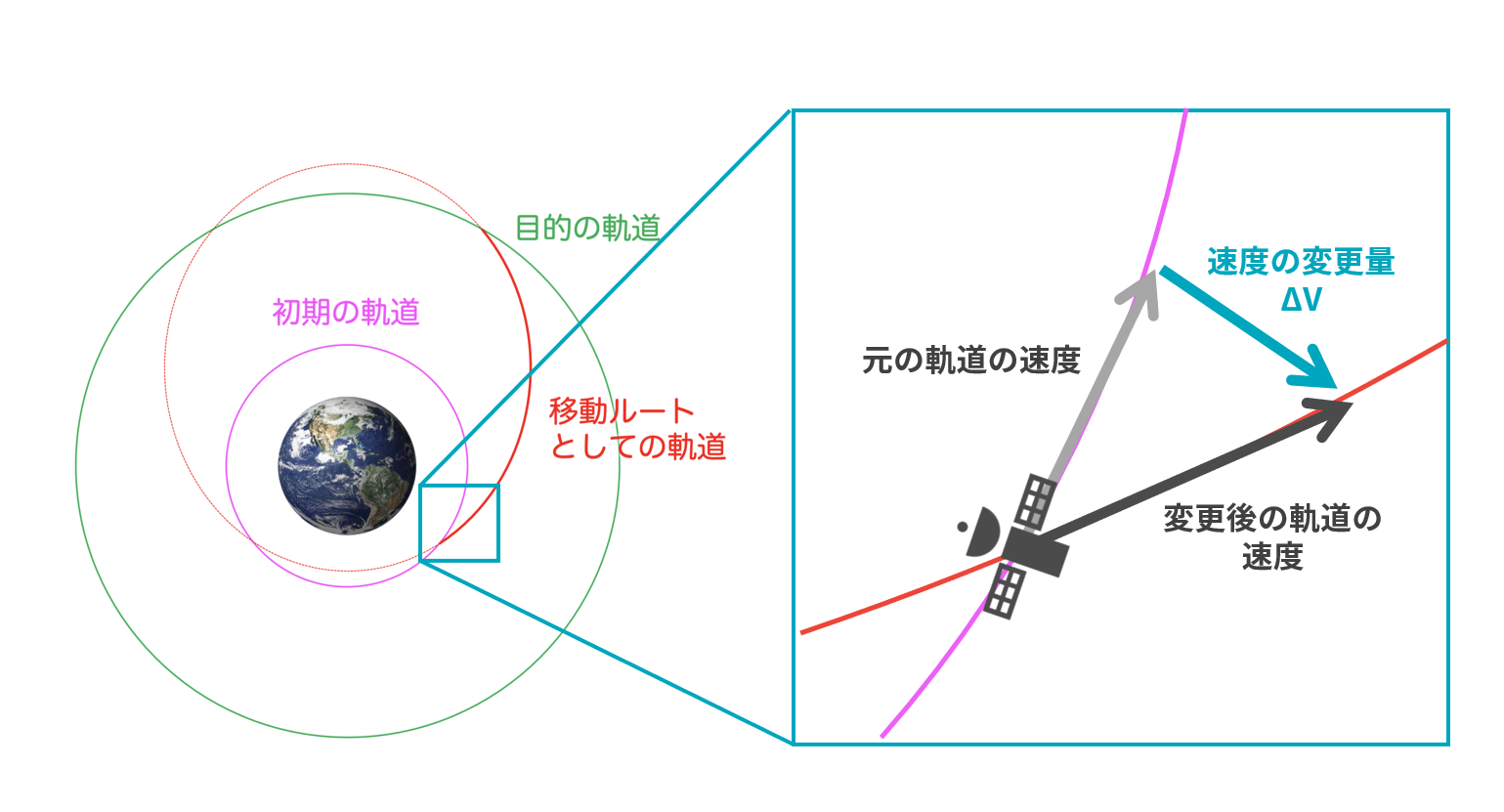
「初期の軌道」から「移動ルートとしての軌道」への変更

そして，「初期の軌道」と「移動ルートとしての軌道」が交わる位置で速度を変更すれば、「移動ルートとしての軌道」に乗り換えることが可能となります。ここで、速度の変更量はΔV（デルタブイ）と呼ばれています。ΔVは速度（ベクトル）の差で計算できます。

そして、「移動ルートとしての軌道」と「目的の軌道」が交わるところで、再び速度を変更することで、目標の軌道に到達することができます。

このような移動ルートとして選べる軌道は、通常、複数通り存在します。そのため、その複数通り存在する移動ルートの中から、ミッションを遂行する上でベストな軌道を選ぶことが求められます。これが私の専門でもある「軌道最適化」です。

どのような観点でベストな軌道を選ぶかはミッションによって様々ですが、ロケットや宇宙機の燃料消費量が少なくなるような軌道を選ぶ場合が多いです。

軌道変更にともなう燃料消費量の計算

ロケットの燃料消費量は「ツィオルコフスキーのロケット方程式」を用いて計算することができます。ツィオルコフスキーのロケット方程式の導出は様々な教科書に紹介されているので、ここでは割愛します。

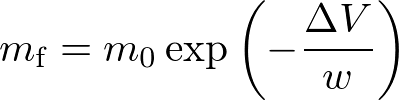
有効排気速度はロケットの性能を表す量であり、大きければ大きいほど効率的です。例えば、固体ロケットであれば2.45km/s程度、液体ロケットであれば3.43km/s程度、はやぶさ等で有名となったイオンエンジンであれば29.4km/s程度です！いかにwの大きなロケットを開発するかが、ロケット推進の研究者の研究課題の一つとなっています。

では、Jupyterノートブックを使って、ロケットが運べる質量を計算してみましょう。LEOから深宇宙空間へギリギリ脱出するためには、約3.3km/sのΔVが必要です（第二宇宙速度11.2km/sと第一宇宙速度7.9km/sの差で計算できる）。初期質量1000kgの液体ロケットを仮定して、LEOから深宇宙まで運べる質量を計算してみましょう。

import numpy as np
dv = 3.3 # LEOから深宇宙へのΔV，km/s
w = 3.43 # 液体ロケットの有効排気速度，km/s
m0 = 1000 # 初期質量, kg
mf = m0*np.exp(-dv/w)
print(mf)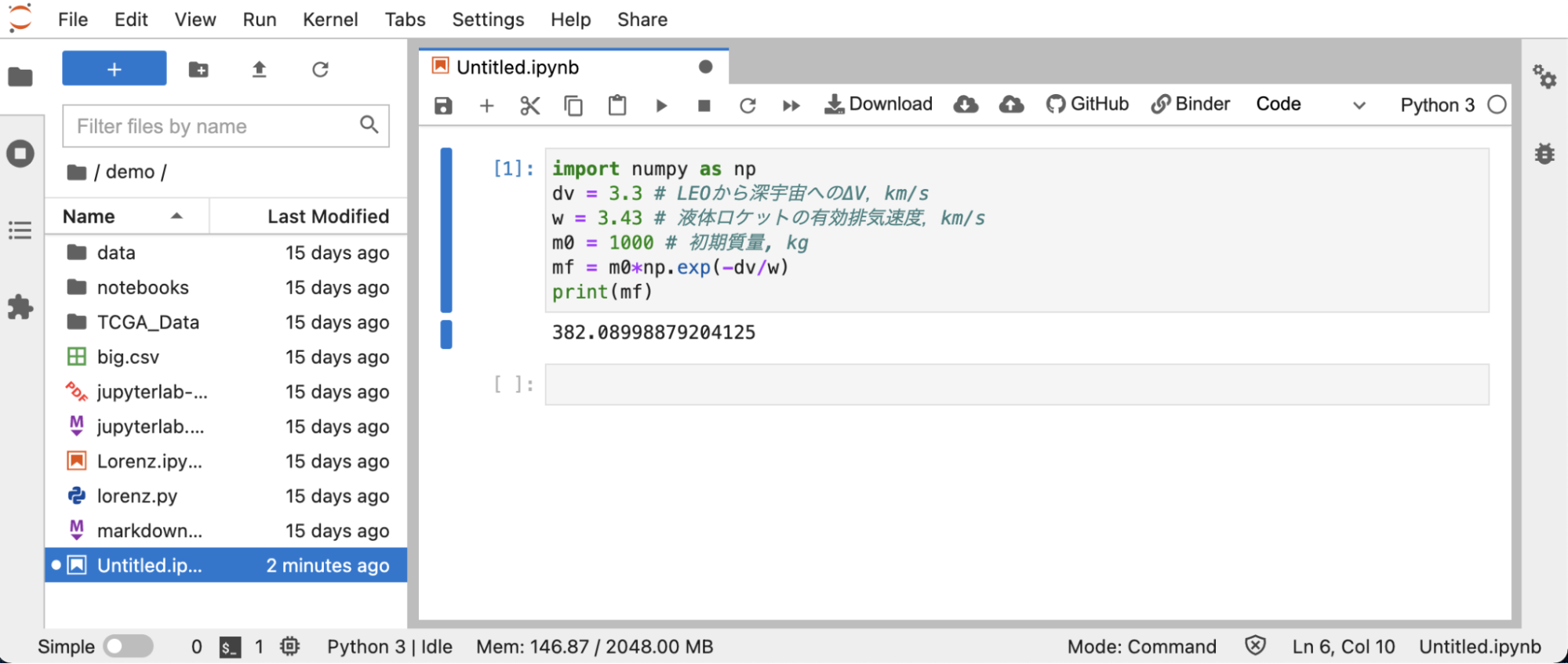

これはつまり、1000kgの液体ロケットで運んだ場合、約6割の618kg（1000kg – 382kg）は燃料として消えてしまうということです！この残った質量382kgにはロケット推進のハードウェア、タンク、それらを支える構造等も含んでいるので、注意が必要です。ΔVの大きさ・wの大きさが、いかに大切かが分かっていただけましたでしょうか。

それでは、ΔVの計算するための手法をいくつか紹介します。ただし、実際のΔVの計算は非常に奥深いため、今回は入門編になります。より詳しく勉強したい方は、書籍などを参照してください。以下では、全て二体問題を仮定します。

ホーマン遷移軌道

初期の軌道と目的の軌道が共に同一平面の円軌道であるとき、ΔV最小の遷移軌道として、「ホーマン遷移軌道(Hohmann Transfer Orbit)」という軌道が知られています。

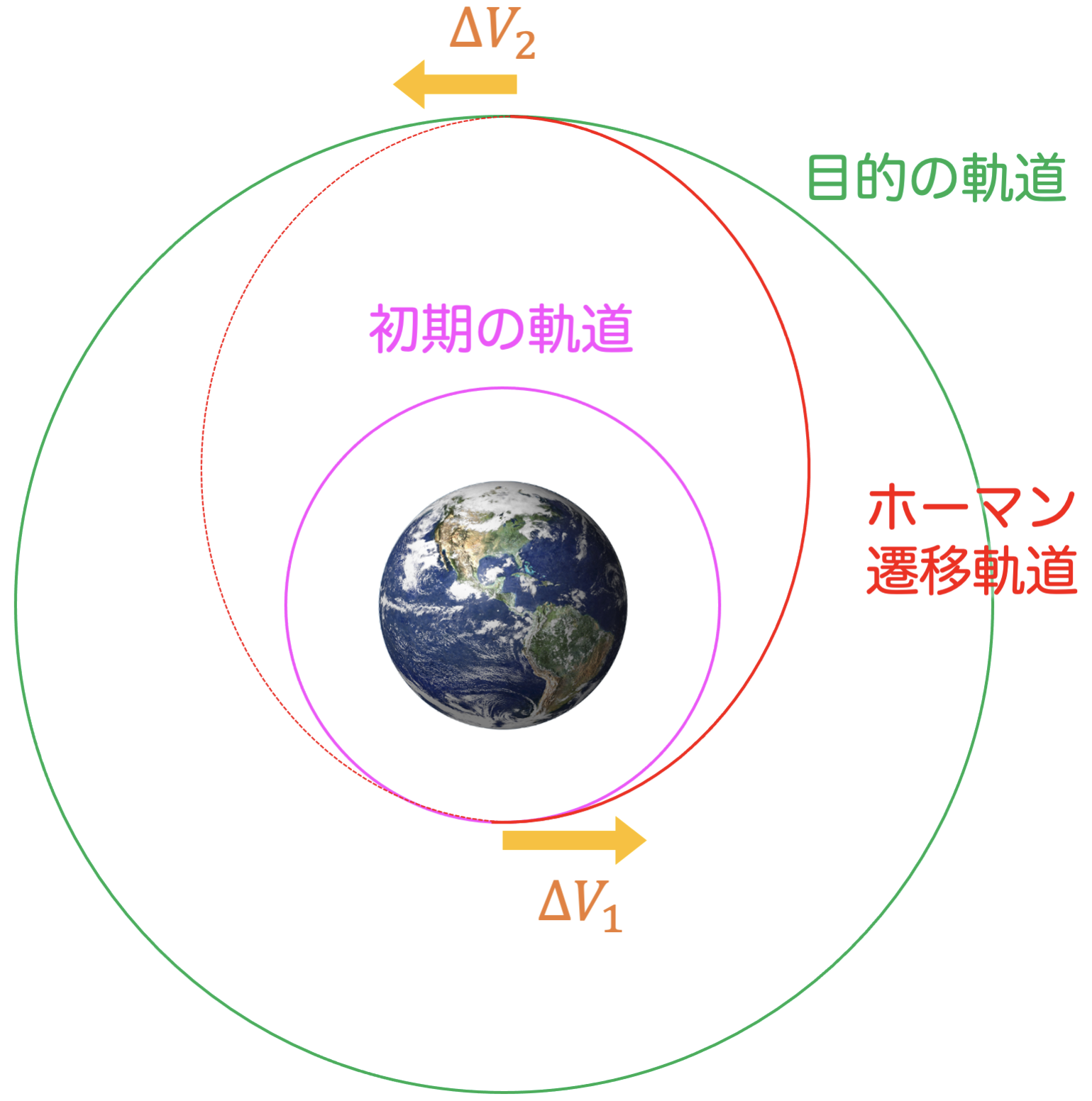
ホーマン遷移軌道は、内側の円軌道上に近点が、外側の円軌道上に遠点があるような楕円軌道です。

なぜホーマン遷移軌道がΔV最小になるかを直感的に説明すると、衛星が進行方向にΔVを与えた方が効率的であるためです。ホーマン遷移軌道によらず、速度方向にΔVを出すと効率的に遷移できることが多いです。

楕円の近点半径をrp、遠点半径をraとしたとき、楕円の近点・遠点での速度は以下の式で計算できます。

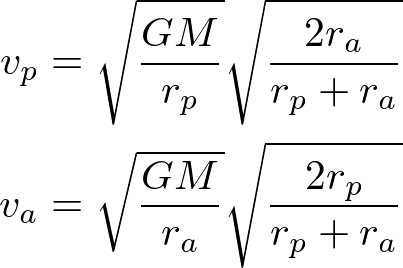
なお、この式は楕円軌道が近点と遠点でエネルギー・角運動量が保存されるという以下の関係式から導かれます。

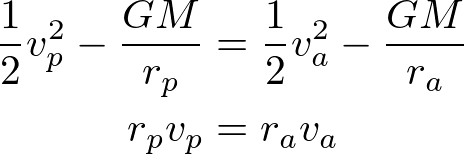
では、低軌道（軌道半径6778km）から静止軌道（軌道半径42164km）へ遷移するために必要なΔVをJupyterノートブックで計算してみましょう。

import numpy as np
# 計算条件
GM = 398600.4354360959 # 地球の重力定数, km3/s2
rp = 6778 # LEOの軌道半径, km
ra = 42164 # GEOの軌道半径, km

# LEOの軌道速度とGEOの軌道速度
v_LEO = np.sqrt(GM/rp)*np.sqrt(2*rp/(rp+rp)) # 円軌道なので近点半径・遠点半径共にrp
v_GEO = np.sqrt(GM/ra)*np.sqrt(2*ra/(ra+ra)) # 円軌道なので近点半径・遠点半径共にra

# ホーマン遷移軌道の速度
vp = np.sqrt(GM/rp)*np.sqrt(2*ra/(rp+ra))
va = np.sqrt(GM/ra)*np.sqrt(2*rp/(rp+ra))

# ΔV計算
dv1 = vp-v_LEO
dv2 = v_GEO-va

print(dv1, dv2)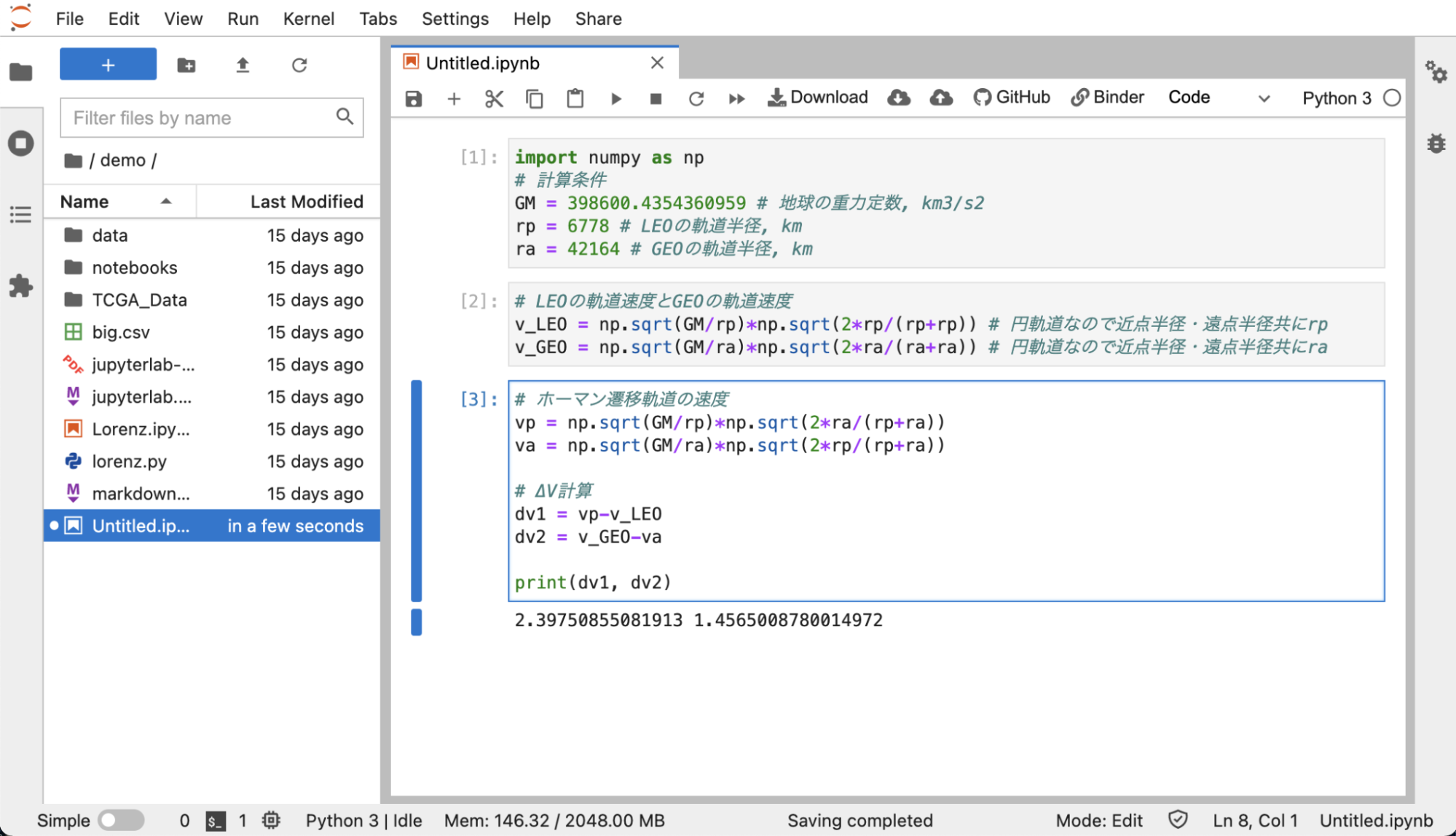

このような低軌道からGEOへの遷移軌道は静止トランスファ軌道(Geostationary Transfer Orbit: GTO)と呼ばれています。ここで計算されたΔV1は通常ロケット側で、ΔV2は衛星側で出すように設計することが多いです。衛星側で必要なΔV2=1.46km/sを出すために、どのくらいの燃料が必要かはロケット方程式で計算してみてもらえればと思います。

ランベール問題

ホーマン遷移軌道は、「初期の軌道と目的の軌道が共に同一平面の円軌道であるとき」という条件の元で成立していました。しかし、実際の軌道の多くは、同一平面でも、円軌道でもないことが多いです。

一般的な軌道間遷移計算の方法として、専門家の間でも広く使われている手法に「ランベール問題(Lambert’s Problem)」の解法があります。

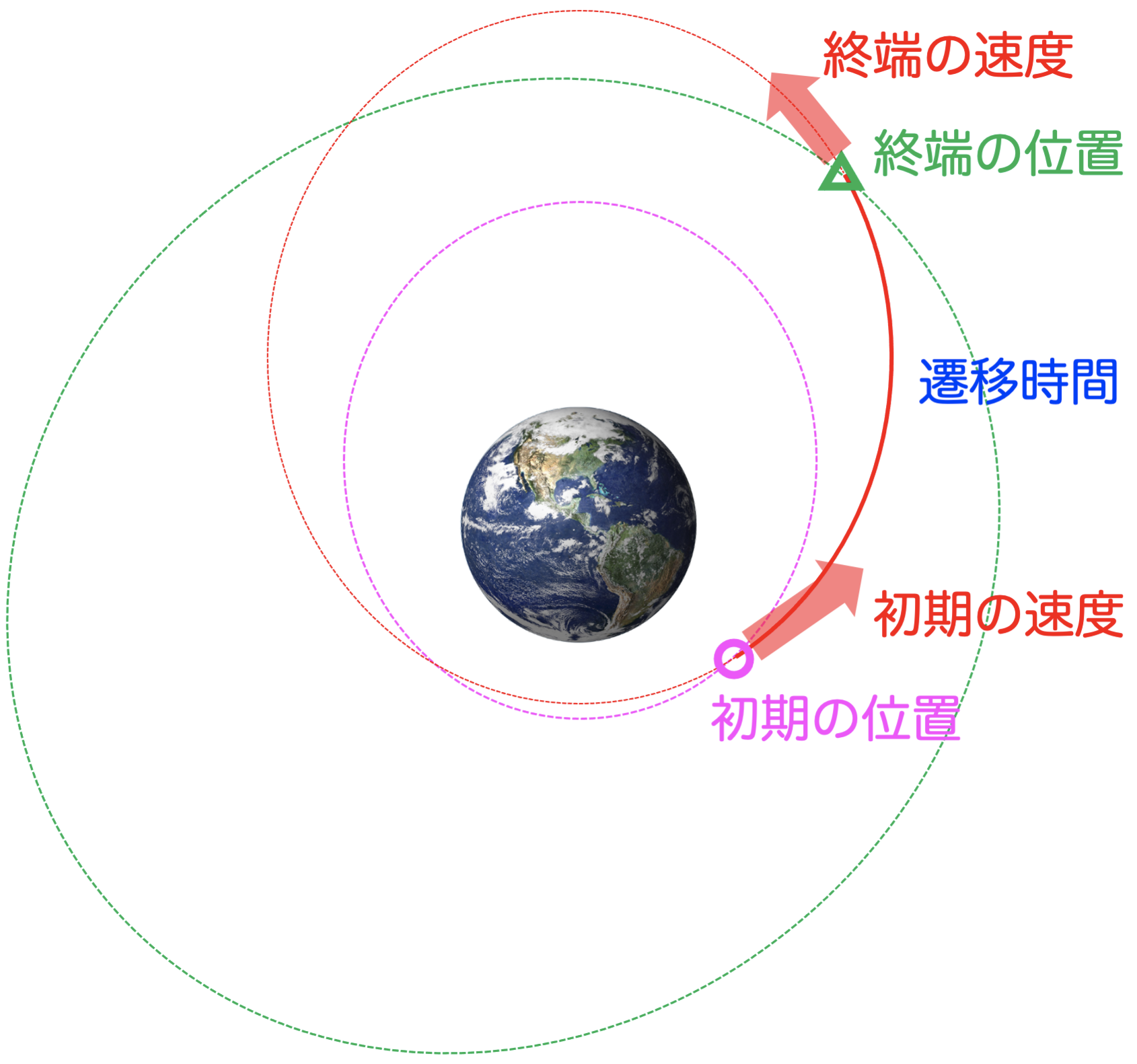
ランベール問題の理論的な説明には何時間もの時間を要するため、ここではその結果のみを紹介します。ランベール問題は、初期の位置、終端の位置、そして、その遷移時間が与えられたときに、初期の速度、終端の速度を計算するという問題です。

では、Jupyterノートブックを利用して、ランベール問題を解いてみましょう。pykepが必要なので、もしインストールされていなければ、改めてインストールが必要です。

import pykep as pk
import numpy as np

# 計算条件
# 注意: r1ベクトルとr2ベクトルが同一直線上に来る場合は，Lambert問題を
# 一意に解くことができないので，少しずらしている
GM = 398600.4354360959 # 地球の重力定数, km3/s2
r1 = np.array([0.01, -6778.0, 0.0]) # LEO上の位置, km
r2 = np.array([0.01, 42164.0, 0.0]) # GEO上の位置, km
tof = 19048.4026989538 # GTO半周分の時間, s

# Lambert問題を解く
l = pk.lambert_problem(r1 = r1, r2 = r2, tof = tof, mu = GM)

# ΔVの計算
v_LEO = np.sqrt(GM/6778.0) # LEOの速度, km/s
v_GEO = np.sqrt(GM/42164.0) # GEOの速度, km/s
v1 = l.get_v1()[0] # Lambert問題から計算された初期の速度
v2 = l.get_v2()[0] # Lambert問題から計算された終端の速度
dv1 = abs(v1[0]) - v_LEO
dv2 = v_GEO - abs(v2[0])

print(dv1, dv2)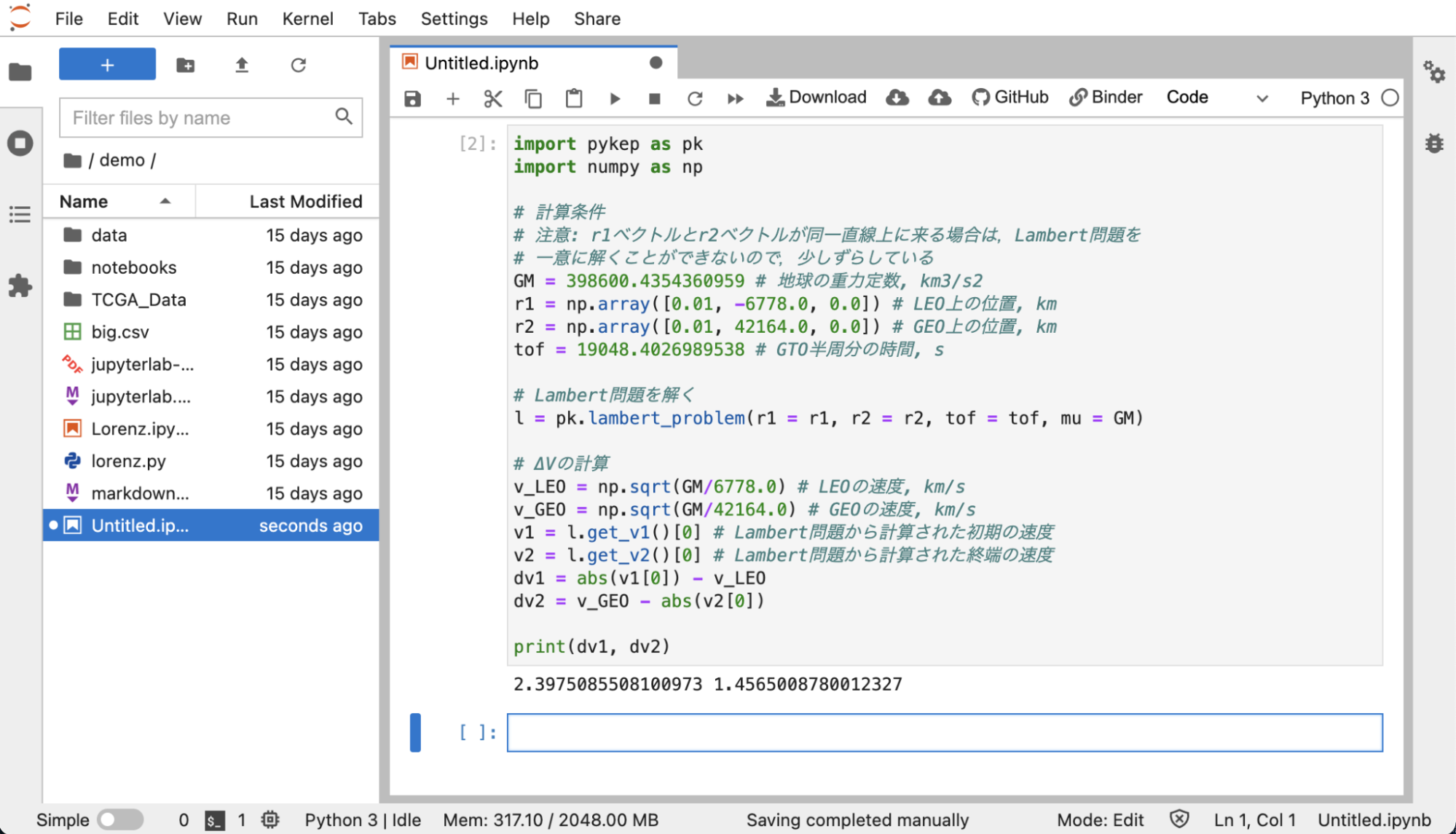

ホーマン遷移軌道で計算したものとほとんど同じ結果が得られたでしょうか？ランベール問題を解くことで、より一般的な遷移軌道を計算することが可能になります。ここで、ランベール問題は初期の軌道から目標の軌道への”最適な”遷移軌道を計算するものではないということに注意してください。最適な遷移軌道を計算するためには、初期の位置、終端の位置、遷移時間を変えながら、軌道を探索する必要があります。

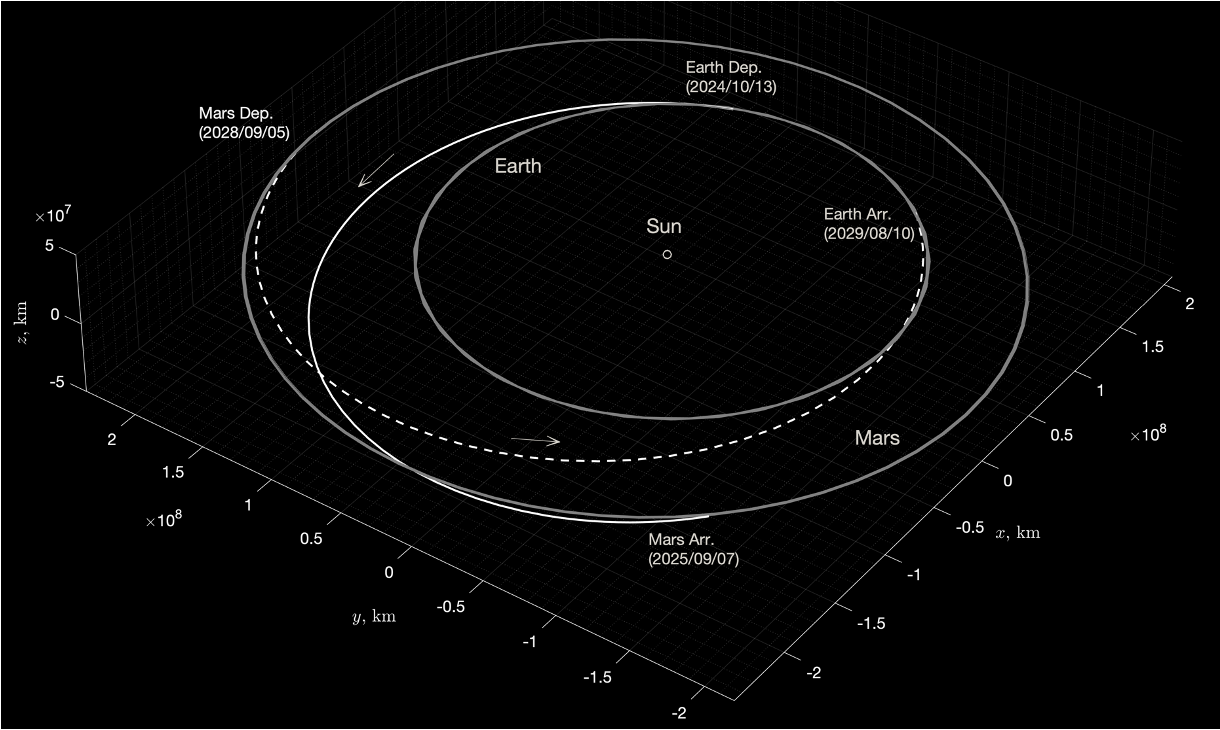
ランベール問題はJAXAの火星衛星探査計画MMXの地球＝火星間軌道遷移にも用いられているます。ただし、地球や火星等の重力天体を扱う場合、重力天体近傍で軌道が曲げられる効果を考えなければいけません。このような問題を扱うために、「パッチドコニックス」というアプローチが使われることが多いです。

将来展望

本記事では、人工衛星と宇宙機の軌道に関して「目的地としての軌道」と「移動ルートとしての軌道」の２種類の観点から説明してきました。また、本記事では触れませんでしたが、近年問題視されている宇宙デブリに関して、他の衛星に衝突しないか評価したり、何年後に大気圏に突入するかを評価するためにも、軌道解析（主に軌道伝播が用いられます）が欠かせません。本記事は軌道に関する入門の話でしたが、ミッションにとって有利な軌道・効率的な遷移軌道を計算するには、より高度な知識が必要となります。

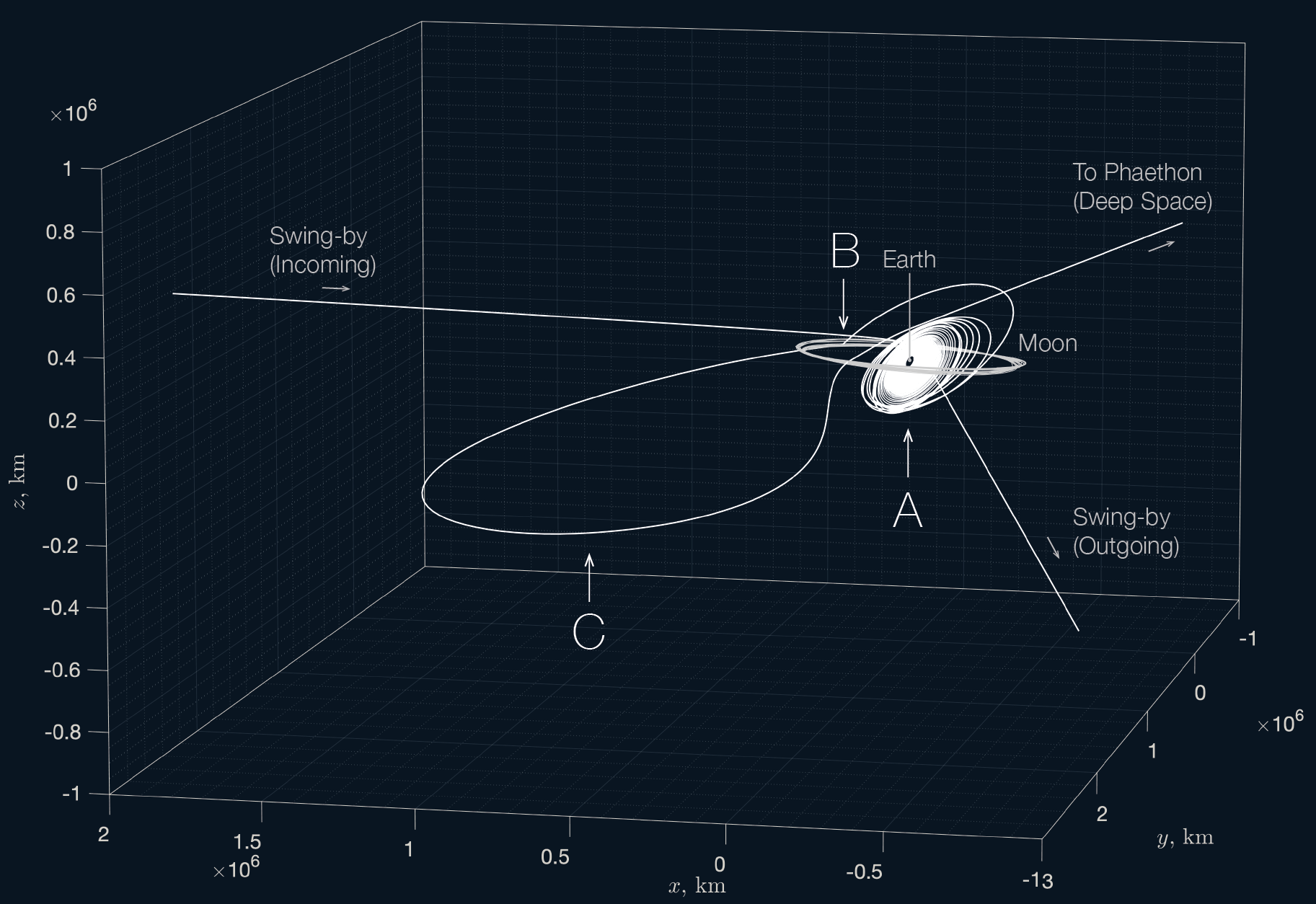
例えば、JAXAが2020年代に打上げを目指している深宇宙探査技術実証機DESTINY+では、はやぶさやはやぶさ２で開発されたイオンエンジンによるスパイラル軌道制御、ひてんやのぞみで用いられた月マルチスイングバイ技術が併用されることで、小型ロケットでも深宇宙探査ができる世界を切り拓こうとしています。

地上で旅行をする場合、近年、カーナビやGoogleマップが普及したため、綿密な計画を立てずとも旅行ができるようになりました。しかし、宇宙の旅は、現状、軌道の専門家に頼らないと目的地や移動ルートを決められない状態です。今後、アルテミス計画や月軌道ゲートウェイを通じた宇宙利用・宇宙ビジネスが拡大していく中で、軌道に関するニーズはますます拡大していくと考えています。本記事をきっかけに多くの読者に軌道について興味を持っていただければ幸いです。

人工衛星の軌道に関する宙畑関連記事