YAMAPのリアルタイム紅葉モニターの画像を参照して衛星データから紅葉予測チャレンジ!~データ解析編~
春の桜と並ぶ、日本の四季の楽しみ方である秋の紅葉について、衛星データで見頃を予測できないかと考えた宙畑編集部。YAMAPのリアルタイム紅葉モニターの画像をお借りしながら、高尾山の紅葉時期予測を行いました。
本記事は前回公開した紅葉予測記事の後編です。
本企画では、衛星データを用いて紅葉の色づき具合のモニタリングや予測を行うことを目指しています。前編では、前準備として予測に用いるためのデータやNDVIの算出用コードを用意しました。
後編となる本記事では、考案した具体的なアルゴリズムの内容と結果を紹介します。
YAMAPのリアルタイム紅葉モニターの画像を参照して衛星データから紅葉予測チャレンジ!~データ確認編~
紅葉モニタリング・予測 アルゴリズムの流れ
前編でも紹介しましたが、紅葉予測にはNDVI指数が多く用いられています (NDVIについては、例えばこちらの記事をご覧下さい)。前例にならい、今回も簡単にNDVIの閾値に基づいて紅葉具合を判定できないか試みます(※1)。
具体的には、木々の葉の色が月日と共に変化していくにつれ、その領域におけるNDVI指数も変化することから、このNDVIがある閾値程度に達したら紅葉がピークをむかえていると判定するようなアルゴリズムを考えることにしました。
そこで問題になるのは、そのようなNDVIに対する閾値はどうやって得るかということです。というのも、場所によって生えている木の種類も違うため、紅葉具合の指標とするNDVIの閾値も場所によって違うはずだから。
その閾値を明らかにするためにYAMAPから提供いただいたSNSデータを使用してみたのが今回の記事の肝になります。
SNSデータとはすなわち、登山者の方々がYAMAPのアプリ上で投稿している登山道の写真データです。これらの写真データは、衛星データでは直接見ることができない地上の紅葉具合の把握に使えるため、衛星データの予測モデルの調整に使用できます。
そこで、これらのSNSデータをもとに自動で閾値を得る方法を考え、NDVIの値がその値に達すると見込まれる日にちを持って紅葉の予測を行うことにしました。まとめると、具体的な紅葉予測アルゴリズムの流れは以下のようになります。
以下に、上記手法をより詳細に見ていきます。ここでは議論の簡単化のために、興味の対象領域を高尾山とし、データが豊富に揃っている2020年のデータを主に用いて、NDVIの閾値を計算します。得られた閾値と2022年のこれまでのNDVIの時間進化を照らし合わせることで、今年の高尾山における紅葉が最も綺麗になる日にちの予測を行います。
Step1. NDVI時間進化の計算
さて、今回はNDVIの値を元に紅葉予測を行おうとしているのでNDVIの時間進化を計算することが必要です。これに関しては前編の記事ですでに行いました。
ただ、前編でも見たように衛星データのデータ数は多くありません。そのため、関数フィッティングをしてデータ間の領域を補間することにしました。また、ここで得られたフィッティング結果は将来のNDVIの時間進化の予測にも使用できます。
ここでは、参考文献[1]に習ってシグモイド型の関数でフィッティングすることにしました。高尾山における2020年6月~2021年2月のNDVIデータとそのフィッティング結果が以下のようになります(フィッティングの詳細に関してはAppendix Aをご参照下さい)。
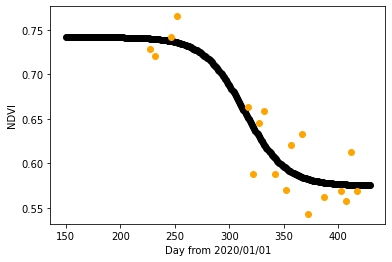
紅葉が色づくに従ってNDVIの値が減少していく傾向が見て取れますね。
Step2. 紅葉が色づく時期のNDVI値(=閾値)の算出
まず、紅葉が最も色づいていく時期に対応するNDVIの値(=閾値)を算出します。同じ場所(=高尾山)では木々の種類が基本的には変化しないことを考えると、このように紅葉がピークとなるNDVIの閾値は年によってあまり変化しないと考えられます。
そこで、予測したい年(=2022年)より以前の年のYAMAPにいただいた地上データを使用して閾値を求めることにします。ここでは2020年6月~2021年2月におけるデータを用います。
YAMAPから提供いただいたデータは、登山者が撮影した登山道における写真データです。そのため、もちろん写真は紅葉が写っているものもあれば、看板を写したものや花を写したものなど様々なものがあります。ここからどうやって紅葉具合を評価すれば良いのでしょうか?
そこで考えたのが、写真データにおける赤色成分が卓越している画像は紅葉を写している可能性が高いのではないか、という仮説です。
そこで、簡易的ではありますが、写真データのR, G, B成分についてそれぞれ画像平均を取った時に、R成分が一番高い値を示している画像を「紅葉が写っている可能性が高い画像」と判断することにしました。
実際この仮説に従って、「紅葉が写っている可能性が高い画像」として抽出されたものの例が以下になります。ご覧のように、多くの写真に紅葉が写っていることが分かります。

また、そうでない画像(GまたはB成分が卓越している)として抽出された画像の例が以下のようになります。紅葉がさほど色づいていない画像や、紅葉とは関係のない画像が多く見受けられます。

このように、もちろん完全ではないものの、上記の簡易的な手法によってざっくりと紅葉が色づいている写真とそれほどでもない写真に分けられているのではないかと思います。
各日にちについて、投稿されている写真データの枚数のうち、このようなR成分が一番高い値を示す写真の割合を「紅葉度合い」と近似して、これを各日にちについてプロットしたのが以下になります。図は2020年の高尾山について示しており、データ点を2次関数でフィッティングした曲線も載せてあります。
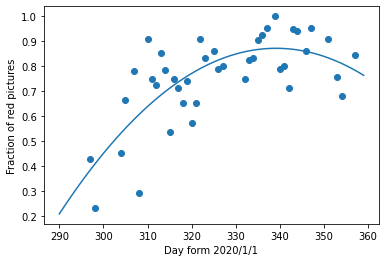
これより、2020年度において「紅葉度合い」がピークとなったのは元旦から数えて339日め、すなわち12月5日頃に対応していることが分かります。これと、前節で見た2020年におけるNDVIの時間進化と比べることにより、NDVIの値が0.61程度のときに紅葉具合が最も高いことが分かります。
Step3. 今年度の紅葉予測
それでは、いよいよ今年度の紅葉予測を行います。今年度のこれまでのNDVIの時間進化とそのフィッティングを計算し、Stepで分かったように、NDVIの値が0.61あたりになると見込まれる日が紅葉ピークの予測日となります。
まずは、今年のこれまで取得されているSentinel-2のデータを用いてNDVIの値を計算してみます。ただし、ここで大きな問題がありました。今年の11/6時点で、予測に使えそうなデータが2点しかありませんでした。運悪く衛星が撮影した日が曇りばかりだったのかもしれません。フィッティングで得ようとしているパラメータの数は4つなので、データ点が2点だけだとデータ数が少なすぎてフィッティングが不可能です。
そこで、ここでは便宜上データの水増しを施すことにしました。6/1~10/1と1/1~2/28の期間については紅葉が変化する前/し終わった後と想定されるため、年度によらずNDVI値は同時期においてさほど変わらないと思われます。
そこで、フィッティング時には今年度のデータに加え、2020/6/1~2020/10/1、2021/1/1~2021/2/28の過去のデータも使用することにしました。
下図がこうして得られたデータ点とそれに対するフィッティング結果です。赤色が今年度の11/6時点で得られているデータで、オレンジが2020/6/1~2020/10/1、2021/1/1~2021/2/2の過去データになります。
また、フィッティング結果のうち、黒線は本記事を執筆時点までの期間(~2022/11/6)までの期間を表し、灰色領域は今後の予測を表します。
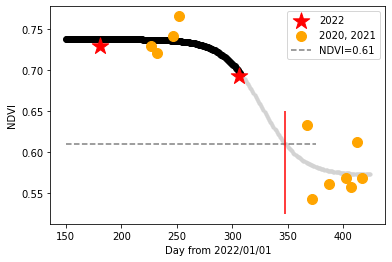
これより、予測曲線がNDVI閾値0.61を横切ると予測されるのは、348日目、すなわち12/13頃となります。以上より、今年の高尾山は12月13日ごろに紅葉が見頃を迎えると予測されました。昨年度や例年の体感よりちょっと遅めな気もしますが、今年度実際にいつ頃見頃を迎えるかが楽しみですね(※2)。
振り返りと今後に向けて
前編記事で述べたこととも一部重複しますが、今回用いた簡単な紅葉予測モデルにおいては以下のような課題に直面しました。
・衛星データの観測頻度が不十分: より密にデータ点が得られれば、より高精度な予測ができたのではないかと思います。また、用いている衛星データによっては画像がさほど取得されない領域もあるため、一つの衛星のデータで日本全国に適用可能な紅葉予測モデルを作るのは困難だとも感じました。
・雲によりNDVIの値が大きく影響を受ける: 雲の割合が大きい日は、画像平均を取ったNDVIの値がそれにより大きく変化してしまい、紅葉由来の成分が埋もれてしまいます。
そこで、雲が少ない日という条件で絞ると、ただでさえ少ないデータ数がさらに少なくなります。このように少ないデータ数ではフィッティングで適切な曲線を得ることはしばしば困難だと感じました。
とはいえ、これらの課題は十分乗り越えられると思います。例えば一点目については、観測頻度の高い衛星や、あるいは複数の衛星を用いることで解消できるかもしれません。
また、後者についてはAIで雲除去のモデルを別途作成することで解決できるかもしれません。これらのような課題が克服されて、衛星データ×地上SNSデータを用いた現実的かつ高精度な紅葉予測モデルができる将来も近いかもしれません。
まとめ
今回の企画は、宇宙からみた広域的な情報が得られる衛星データと、地上のSNSデータの掛け合わせの可能性を探って生まれました。
今回の例のように、衛星データでは得られないミクロな情報を提供する地上のSNSデータは、衛星データで作成した予測モデルの調整や検証に使用できることが確認できました。この他にもSNSデータと衛星データが相補的に使用できる場面は他にも色々あるでしょう!
今回の企画に長期間に渡ってご協力いただいた株式会社ヤマップ様にはこの場をお借りして感謝申し上げます。
YAMAPの取り組みを見る
※1. 衛星データを用いた紅葉予測に関する研究論文は多く書かれていますが、本記事では専門的な解析を行うというよりは、比較的簡単なアルゴリズムを作って概念実証を行うことを目指しました。
※2. 本記事で提唱したのはあくまで簡易的なモデルであるため、予測結果はあくまで非常に大まかな目安であり、予測結果の正しさを保証するものではないことをご了承ください。
Appendix A. NDVIのフィッティング
NDVIの時間進化に対するフィッティングは、参考文献[1]に習ってシグモイド型の関数f(x) = c/(1+exp(a+bx)) +dを用いて行いました。フィッティングに関する主要な関数を以下にまとめました。
def sigmoid_like_func(X, a, b, c, d):
return c/(1.0+np.exp(a + b*X))+d
def omit_outlier(x_list, y_list):
x = np.array(x_list)
y = np.array(y_list)
# 平均と標準偏差を算出
mean=y.mean()
sigma=y.std()
# 下限と上限を算出
limit_low=mean-3*sigma
limit_high=mean+3*sigma
print(limit_low, limit_high)
return x[(y>limit_low) & (y150)], y[(y>limit_low) & (y150)]
def fitting_data(x_, y_, fitting_func):
x_list, y_list = omit_outlier(x_, y_)
init_params = np.array([1., -1./300., 1, 0.])
popt, pcov = curve_fit(fitting_func, x_list, y_list, init_params) # poptは最適推定値、pcovは共分散
print(popt)
# フィッティング結果をプロット
x_points = [i for i in range(150, 400)]
for i in range(len(x_points)):#
plt.scatter(x_points[i], sigmoid_like_func(x_points[i], popt[0], popt[1], popt[2], popt[3]), color="black")
plt.scatter(x_list, y_list)
plt.xlabel("Day from 2020/01/01")
plt.ylabel("NDVI")
plt.show()
return popt

