【徹底解説】第3の分解能に特化したハイパースペクトルデータの概要と解析方法、代表企業まとめ
なんとなく分かったようでいて、理解しきれていない……という方へ、ハイパースペクトルセンサーを有する企業やハイパースペクトルデータの解析方法をご紹介します。
はじめに
最近、宇宙ビジネスのニュースでも見かけるようになってきた「ハイパースペクトル」というキーワード。
なんとなく分かったようでいて、理解しきれていない……という方へ、ハイパースペクトルセンサーを有する企業やハイパースペクトルデータの解析方法をご紹介します!
衛星で用いられる3つの分解能
何気なく使っている分解能という言葉ですが、人工衛星による地上観測ではより深い理解を求められることも多々あります。
分解能とは、どれくらいのことが「分かる」のかを示す指標のことで、地球観測衛星による分解能という概念にはいくつかの種類があります。
本記事では、ハイパースペクトルの何がすごいのかを説明するにあたって、前提知識として、それぞれの分解能についてご説明いたします。
空間分解能:どれくらい細かくみえるか
1つ目は、空間分解能です。
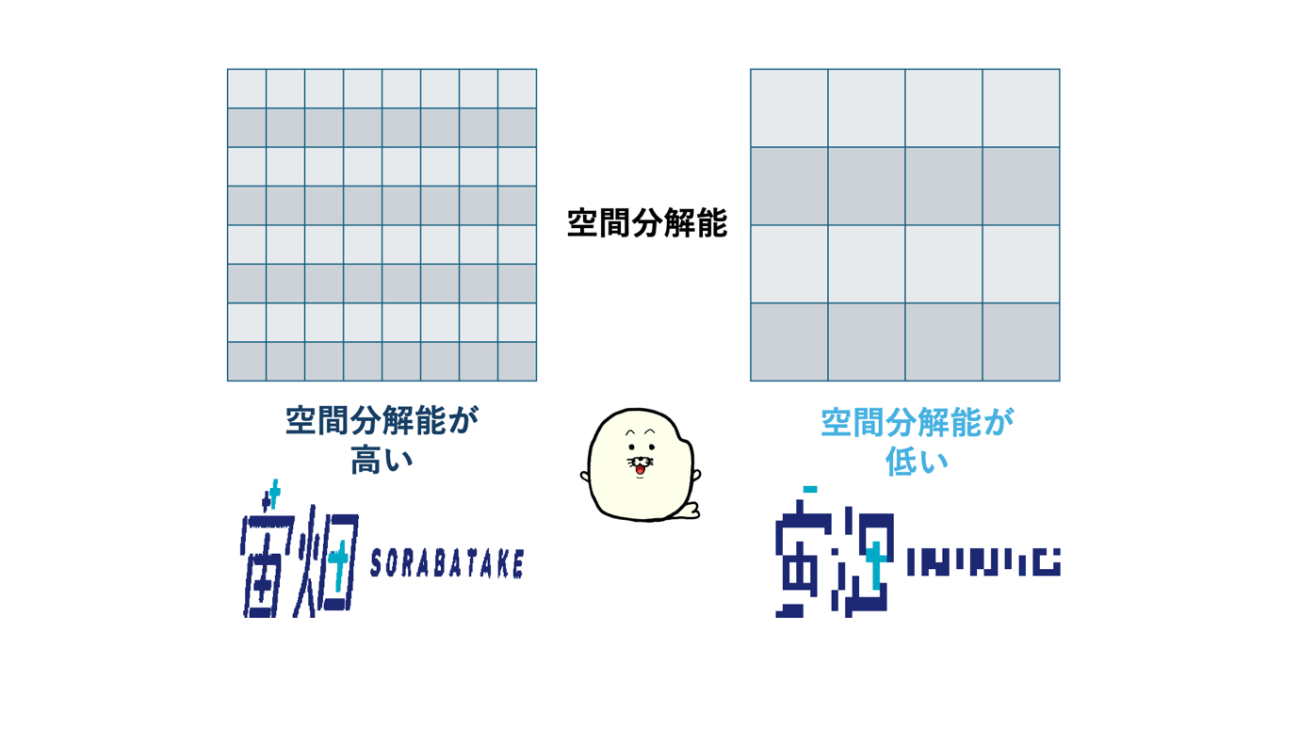
空間分解能とは、画像のピクセル上で地上のどれくらい小さいものが判別できるかを示す能力です。
一般的に分解能というと、この空間分解能を示すことがほとんどです。しかしながら、衛星画像では後述する分解能の種類がいくつかあります。それらと区別するために、地理空間的な意味で「分かる」ことを示す分解能なので、「空間分解能」といいます。
※本記事にも「レーダーの基礎から学ぶSAR(合成開口レーダー)の原理と奇跡」で登場するこめじゃらしくんがでてきます。こめじゃらしくんと一緒にハイパースペクトルの奥深さを学んでいきましょう。
時間分解能:どれくらいの観測頻度で観測するか
2つ目は時間分解能です。
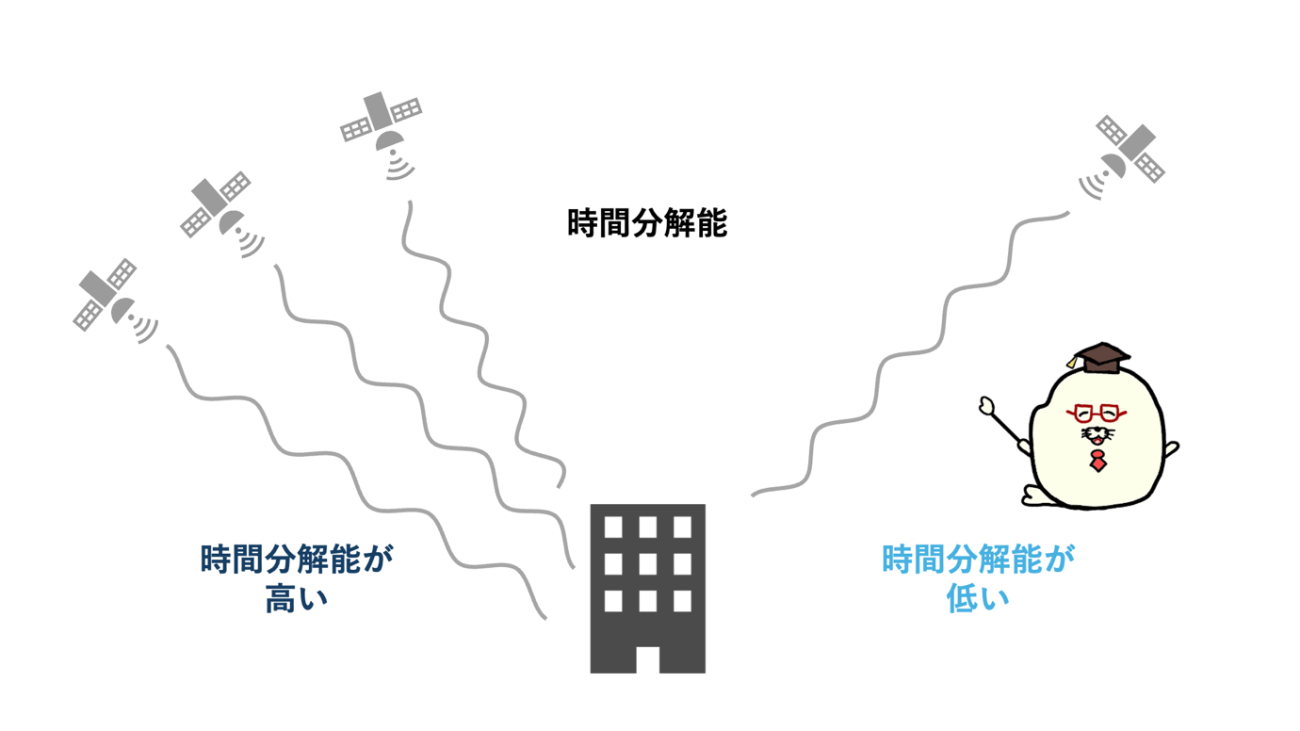
時間分解能とは、衛星画像が撮影される頻度を表しています。
ある地点について観測される頻度が高い場合、観測低い場合と比べて、より詳細な情報を与えてくれます。その情報によって時間的な変化が「分かる」ことから時間分解能といいます。
波長分解能:何色で見られるか
3つ目が、波長分解能です。
私たちが普段、カメラで写真を撮影する場合、一般的には、青、緑、赤の3つの波長で撮影、表示を行っています。
人工衛星による地上観測では、このような3色以外の波長でも撮影を行っています。
人工衛星には、人間の目で見える可視光の波長だけではなく、人間の目には見えないような領域の電磁波も観測するセンサーを搭載しています。地球観測衛星の用語では、この一つひとつの波長のことをバンドと呼ばれています。
例えば、一般的なカラー写真には含まれない赤外線の波長で観測すると、地上の熱を観測することができます。
波長の種類が増えると、カラー画像にはないようなことが「分かる」ことから波長分解能といいます。

空間、時間、波長のうち、第3の波長分解能に特化したデータがハイパースペクトルデータです!!
ハイパースペクトルとは
ハイパースペクトルとは、たくさんの種類の波長で観測した波長ごとの反射強度のことです。
厳密な定義はないですが、数種類(10種類以下)の波長(バンド)で観測するセンサーをマルチスペクトルセンサーといいます。
それに対して、たくさんの種類(10種類以上)の波長で観測するセンサーをハイパースペクトルといいます。ハイパースペクトルは、可視光のように赤、青、緑の3種類や、マルチスペクトルのような4〜9種類の観測とは違って多くの波長分解能を有することが特徴です。
ハイパースペクトルは、宇宙領域特有の観測手法ではありません。地上でも非破壊検査や非破壊解析に利用され、例えば、薬品の濃度分析や鉱物の主成分解析で活用されています。
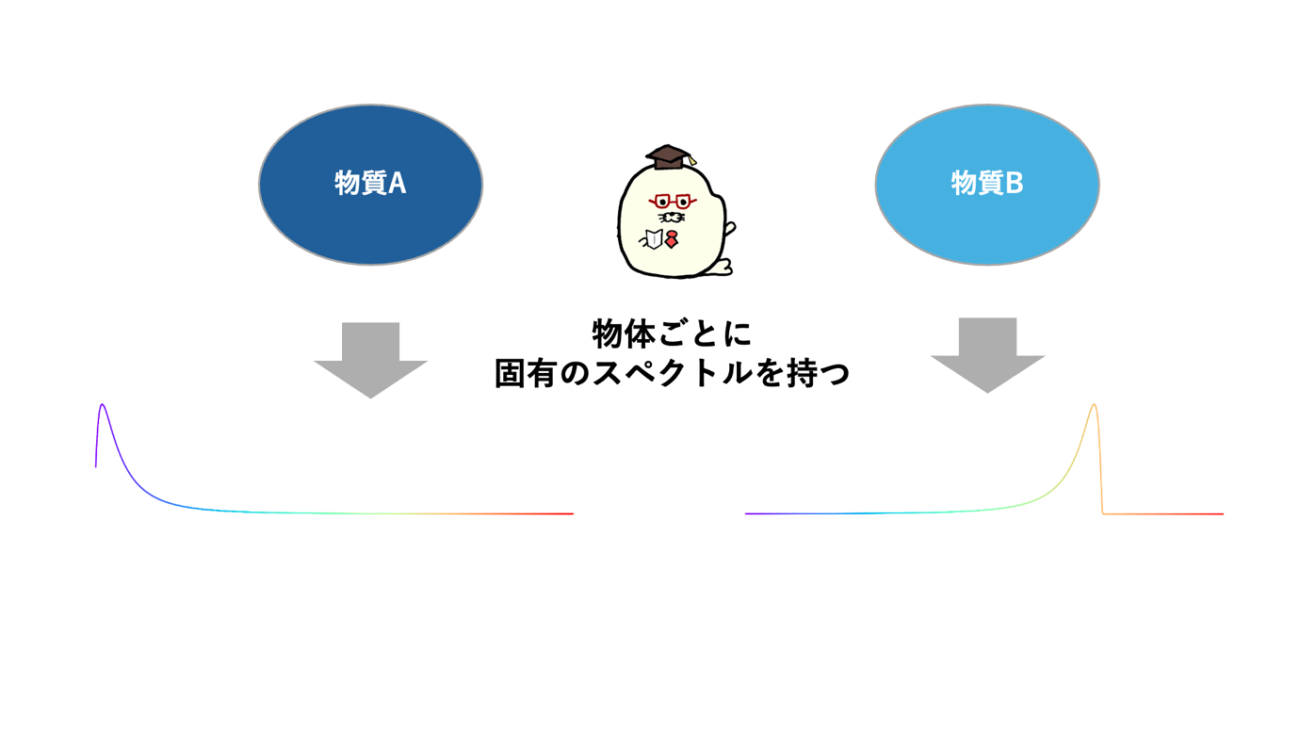
私たちの身の回りにあるモノは、物質ごとにどの波長の電磁波をよく反射するのか、放射するのかは異なっています。その特性を応用し、たくさんの波長における電磁波の”スペクトル”を観察することで、「このスペクトルを持っているということは、あの物質だ!」と物質を特定することができます。
すなわち、波長分解能を高めることで物質の詳細が「分かる」ことになります。
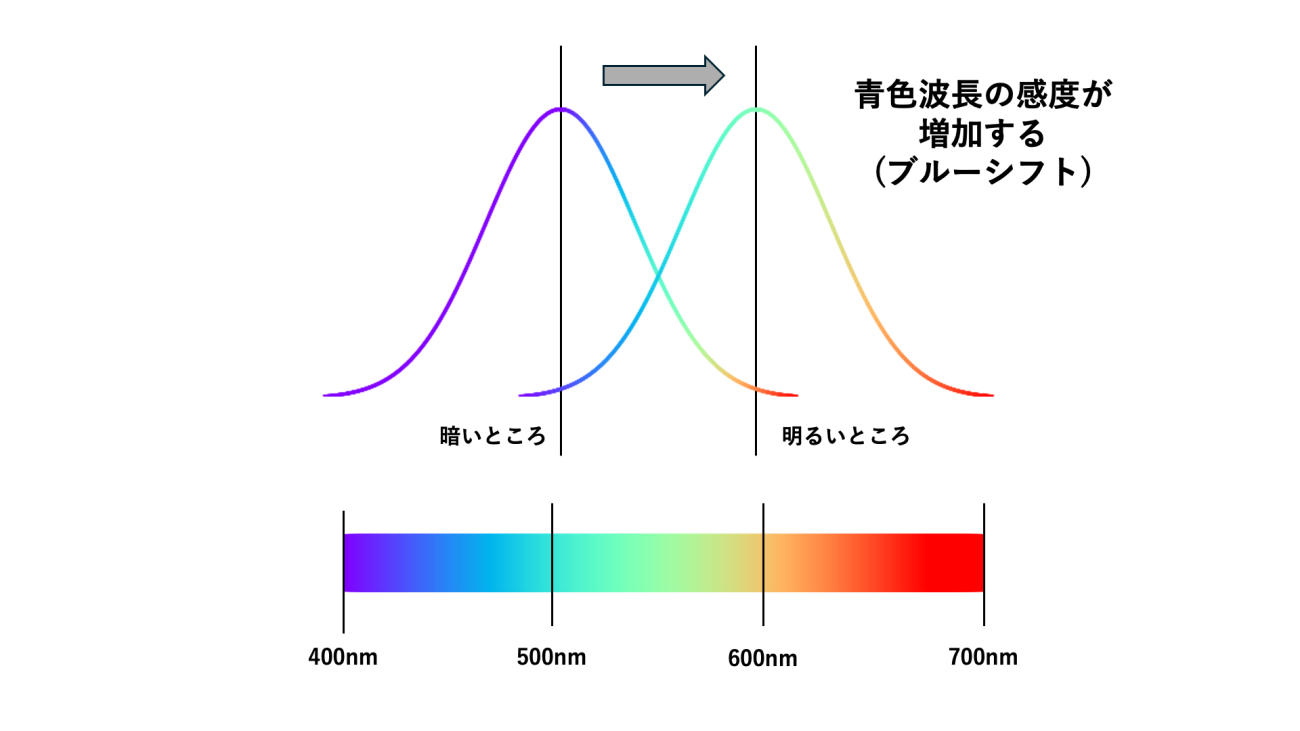
見たい対象によって波長を変化させることは身近にも起きています。
これはプルキンエ現象といって、人間が明るいところから暗いところへ行った際に、短い波長を見て、感度を上げるように目が反応する現象です。また、青色波長方向へスペクトルを移動させることからブルーシフトともいいます。
 ブルーシフト、かっこいいじゃらし!
ブルーシフト、かっこいいじゃらし!
余談にはなりますが、スペクトル上で反対方向に波長が変化することをレッドシフトといいます。宇宙空間が膨張することで電磁波にドップラー効果が働きます。その結果として、レッドシフトが発生します。遠い天体を観測する際には、レッドシフトした波長を観測することでより遠くの天体を観測できます。宇宙が膨張している理由もレッドシフトが起きているために離れていると考えられています。
 身近なことから宇宙まで、波長はしゅごぃじゃらし
身近なことから宇宙まで、波長はしゅごぃじゃらし
高波長分解能のすごいところ
ハイパースペクトルは波長分解能が良いことがわかりました。では、具体的に波長分解能が高いとどうして良いことがあるのでしょうか?例えば、4種類の波長のみを持つセンサーとハイパースペクトルセンサーでの観測結果を比べてみましょう。
ある場所をハイパースペクトルセンサーで観測したスペクトルを可視化してみます。下記の図では、縦軸が反射の強さで、横軸が波長を表しています。波長14周辺の部分で強い反射が観測できています。
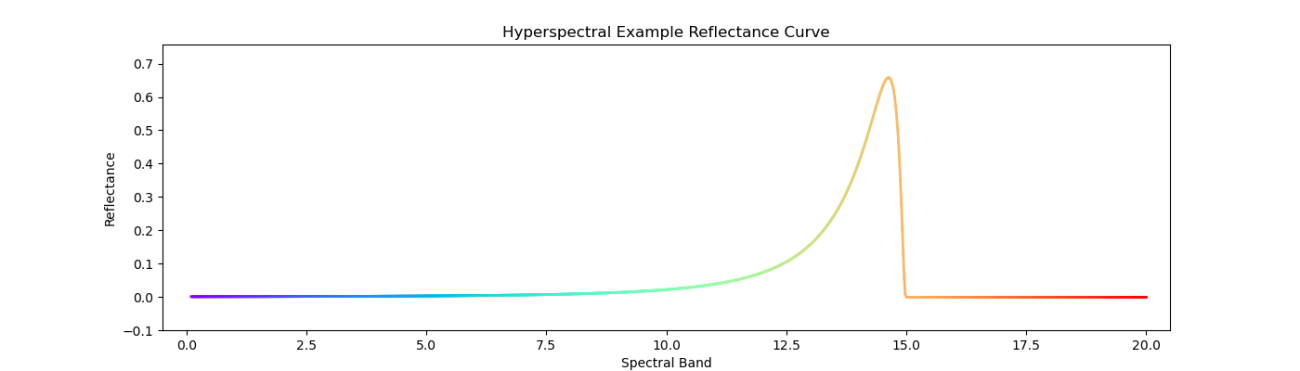
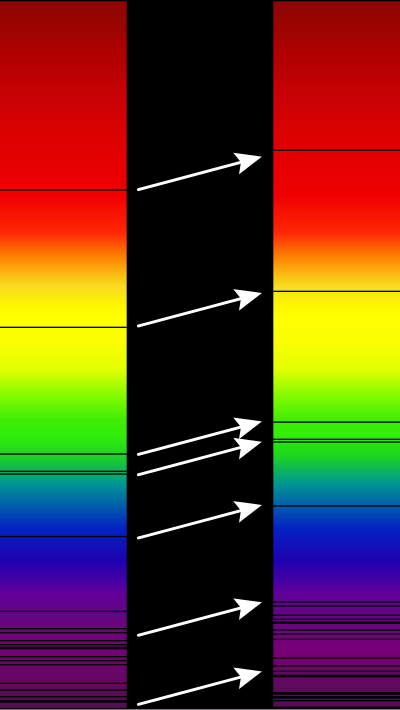
さて、同じ領域を波長4、7、12、19のマルチスペクトルセンサーで観測した結果を可視化してみます。イメージとしては、青、緑、赤、赤外線のような選定です。

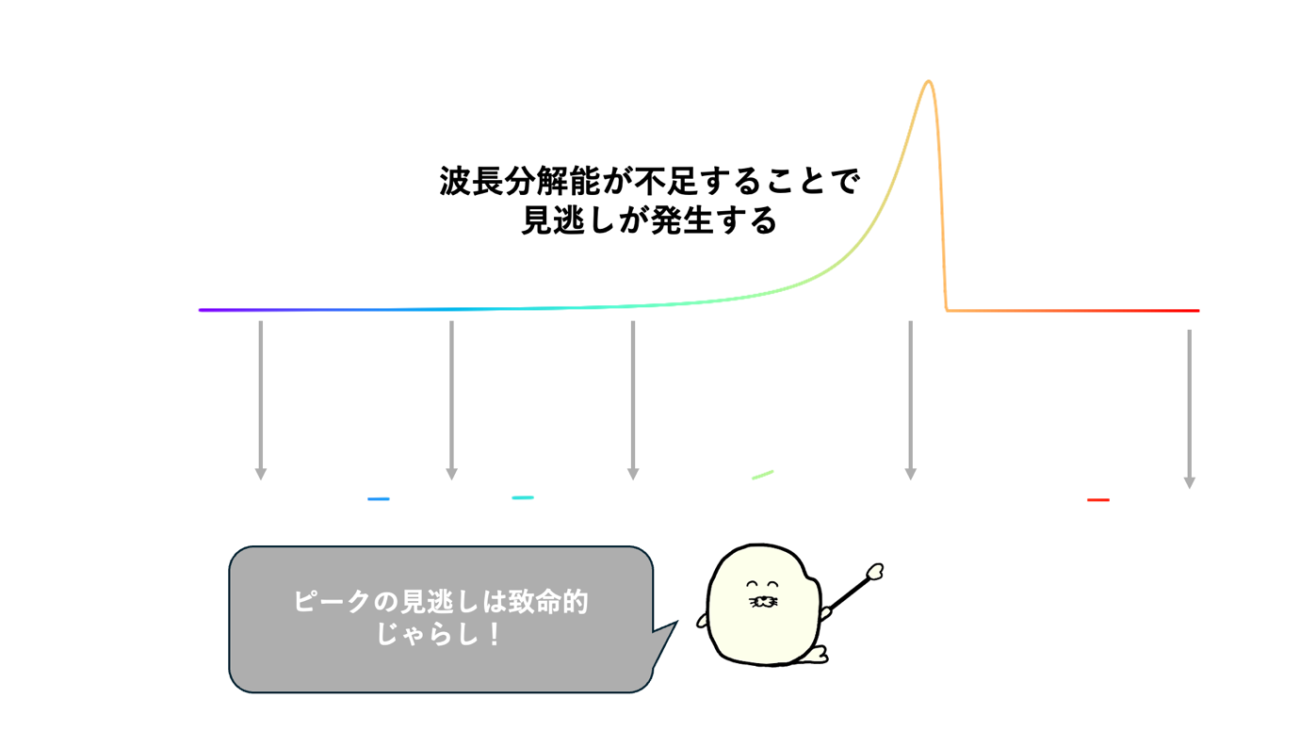
このような例では、波長14周辺でのセンサーがないと観測領域の特有の振る舞いを見分けることが難しいです。マルチスペクトルセンサーでは見逃しが発生してしまいます。
見逃しの領域が多ければ、土壌被覆や物質の分類は難しくなってきます。今まで、光学衛星の画像を確認して「見えなかった」ことが空間分解能だけの問題と思い込んではいないでしょうか?実は第3の分解能である、波長分解能が低かったことも要因になっています。
マルチスペクトルセンサーであっても開発段階で用途が完全に決まっていれば、観測対象に合わせて波長の長さと範囲を決定できます。しかし、実際にはそんなことはほとんどありません。衛星画像は一つの用途だけではなく様々な用途で利用されており、かつ、現在でも新しい用途が開拓され続けているからです。
一方、ハイパースペクトルは先に用途が決まっている必要がありません。むしろ、波長分解能の向上により、観測できる対象を広げ、これまで見えてなかった領域にアプローチすることができます。
また、別の観点では、ハイパースペクトルセンサーの観測情報はマルチスペクトセンサーの基準のような存在にもなり得ます。
マルチスペクトルセンサーを搭載している人工衛星は複数存在します。しかし、それらのセンサーの観測波長は、同じ青だったとしても、ぴったりとは一致していません。
例えば、RGBのカラー画像を生成するための青色波長は、Sentinel-2では450nmですが、Landsatでは中心波長443nmとなっています。近い値ですが、微妙に異なるのです。このような違いが小さければ問題は少ないですが、例えば熱赤外波長1000nm周辺はLandsatにのみ存在し、Sentinel-2には搭載されていません。
ハイパースペクトル衛星はこの異なる衛星間の反射特性を埋めて、補完する基準にすることができます。
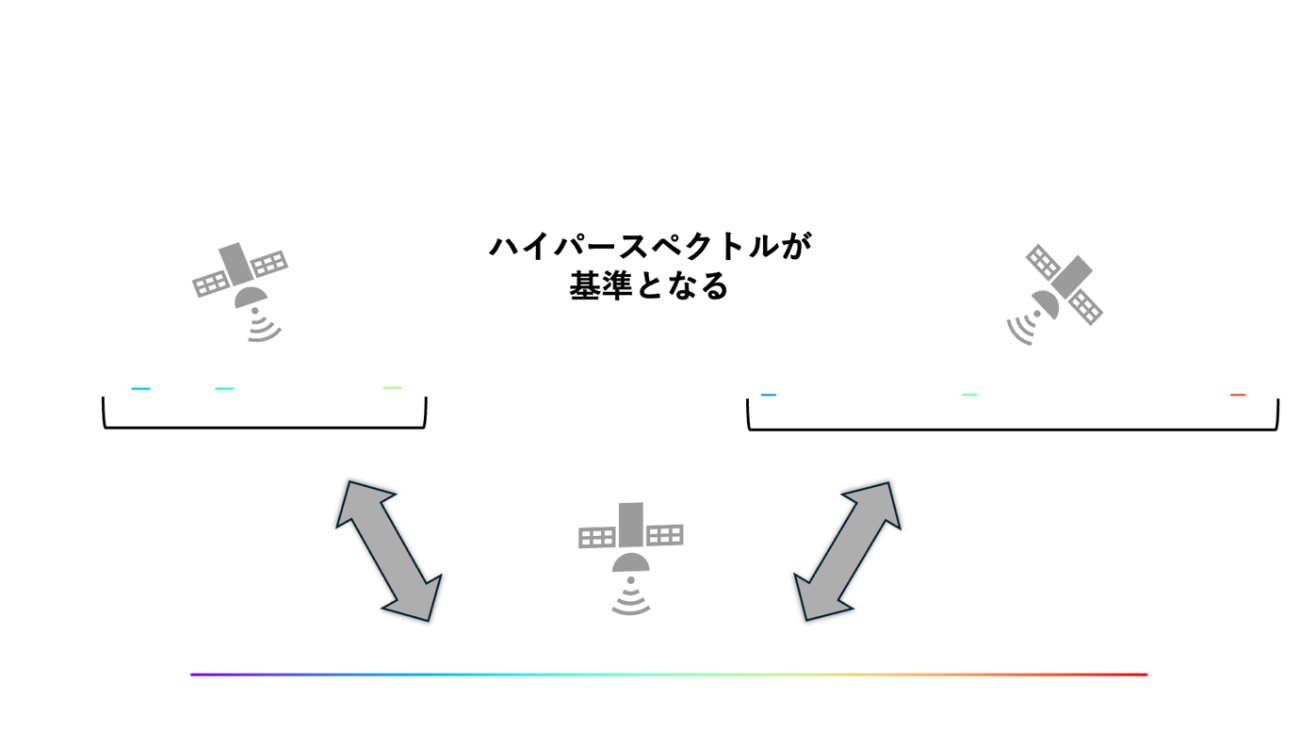
ハイパースペクトルセンサーは、波長分解能が非常に優れており、この特性により異なる衛星間のデータを横断的に比較することが可能になります。
実際に、キャリブレーション(校正作業)やパンシャープン(高解像度の白黒画像と低解像度のカラー画像を組み合わせて高解像度のカラー画像を作成する技術)などの応用にも繋げられています。
ハイパースペクトルセンサー(衛星・航空機)
ハイパースペクトルセンサーの凄さを理解したところで、ハイパースペクトルセンサーを搭載している航空機や衛星のプロジェクトを見ていきましょう。
NASAのハイパースペクトル衛星
1. EMIT(Earth Surface Mineral Dust Source Investigation)
EMITはNASAが開発したハイパースペクトルセンサーで、2022年に国際宇宙ステーション(ISS)に設置されました。このミッションの主な目的は、地表の鉱物ダスト(砂塵)の発生源を特定し、それが気候変動に与える影響を解析することです。
特徴
・可視光から短波赤外領域までのハイパースペクトル観測が可能。
・砂漠や乾燥地帯の鉱物組成を識別し、大気中のエアロゾルの動態を理解するために活用。
・ISSに搭載されているため、地球上の広範囲(高緯度地域を除く)を短期間で観測可能。
応用分野
・気候変動研究(エアロゾルの影響解析)
・鉱物資源探査
・土壌劣化や砂漠化の監視
2. PACE(Plankton, Aerosol, Cloud, ocean Ecosystem)
PACEは2024年にNASAによって打ち上げられた地球観測衛星で、海洋のプランクトン、雲、エアロゾル(大気中の微粒子)を詳細に分析することを目的としています。この衛星にはOCI(Ocean Color Instrument)というハイパースペクトルセンサーが搭載されており、海洋の色の微細な変化を捉えることが可能です。
特徴
・紫外線から近赤外線までと、いくつかの短波長赤外線の広範な波長域をカバーするハイパースペクトルセンサーを搭載。
・地球の高緯度地域が観測可能なので全球解析が出来る。
・気候変動の影響を受ける海洋環境のモニタリングが可能。
応用分野
・海洋生態系の監視(藻類ブルームや生物多様性の評価)
・大気環境の監視(エアロゾルや雲の特性解析)
・水質モニタリング(赤潮や汚染の検出)
NASAのEMITとPACEは、いずれも気候変動や環境問題に焦点を当てたミッションであり、地球システム全体を理解するための貴重なデータを提供しています。
JSSのハイパースペクトル衛星
3. HISUI(Hyperspectral Imager Suite, Tellusプラットフォーム)
HISUIは経済産業省(JSS)が開発したハイパースペクトルセンサーで、2020年にISSに設置されました。このセンサーは、主に鉱物資源探査や環境モニタリングを目的としています。
特徴
・可視光から短波赤外(400~2500nm)までのハイパースペクトルデータを取得可能。
・JAXAが持つ地球観測技術と連携し、災害監視や農業分野にも応用。
応用分野
・鉱物資源探査(鉱床分布の解析)
・環境モニタリング(森林の健康状態評価、都市のヒートアイランド現象の監視)
・災害監視(森林火災や土壌劣化の検出)
JSSのHISUIは、日本国内でのデータ活用を促進するためにTellusプラットフォームと連携し、産業利用も視野に入れた運用を行っている点が特徴です。
プロジェクトの紹介記事で詳しく記載されています
JSS主催「ハイパースペクトルセンサで地球全体を見ると何がわかる?利用事例の最前線と未来」イベントレポート&こぼれ質問に回答_PR
Planetのハイパースペクトル衛星
4. Tanager-1
概要
Planetは商業衛星データを提供する企業で、Tanager-1は同社の最初のハイパースペクトル衛星として2024年に打ち上げられました。この衛星は、環境モニタリングや温室効果ガスの検出を目的として設計されています。
特徴
・400~2500nmのスペクトル範囲を持ち、数百のスペクトルバンドを観測可能。
・高解像度のハイパースペクトルデータを商業利用向けに提供。
・MethaneSATとの協力により、温室効果ガス(メタンなど)の観測精度を向上。
応用分野
・温室効果ガスの排出監視(メタン漏れの検出)
・精密農業(作物の健康状態の診断)
・環境評価(森林破壊や水質汚染の監視)
PlanetのTanager-1は、商業用途に特化したハイパースペクトルデータの提供を目指し、環境保護と産業利用の両立を実現するアプローチを取っています。
以下のニュース記事でも紹介されました。
Planet初のハイパースペクトル衛星「Tanager-1」早ければ7月に打ち上げへ。温室効果ガスの排出を観測【宇宙ビジネスニュース】
WYVERNのハイパースペクトル衛星
5. Dragonette
概要
カナダのスタートアップ企業WYVERNが開発したDragonetteは、商業利用を目的とした小型ハイパースペクトル衛星です。この衛星は、主に農業や林業、環境モニタリング向けに設計されています。
特徴
・小型・軽量で、低コストかつ高頻度の観測が可能。
・数メートル級の空間分解能を持ち、地表の詳細な分析が可能。
応用分野
・精密農業(作物の栄養状態の評価)
・林業(森林の健康状態のモニタリング)
・環境モニタリング(湿地帯の生態系変化の追跡)
WYVERNは、スタートアップ企業ならではの柔軟な運用体制を持ち、特に農業や林業といった分野でのハイパースペクトルデータの実用化を推進しています。
以下のニュース記事で紹介された企業です
ハイパースペクトル衛星を開発するWyvernが約10.2億円の資金調達を発表。来年前半に衛星の初打ち上げへ【宇宙ビジネスニュース】
NASAやJAXAのハイパースペクトル衛星は科学研究や気候変動解析に重点を置く一方で、PlanetやWYVERNの衛星は商業利用を前提にした高頻度のデータ提供を目指しています。今後、ハイパースペクトルデータの活用は、環境保護、資源探査、農業など多岐にわたる分野でさらに広がることが期待されます。
ハイパースペクトルデータのデータ構造
ハイパースペクトルの概要を理解したところで、ハイパースペクトルのデータ構造を理解していきます。
ハイパースペクトルのデータを取り扱う上で重要な概念として、「ハイパースペクトルキューブ」というものがあります。観測した衛星画像を波長ごとに画像を下図のように積み重ねた立方体をハイパースペクトルキューブ(Hyper Spectral Cube)といいます。
画像上の縦と横が空間分解能に対応していて、高さの軸が波長分解能に対応しています。ハイパースペクトルキューブは空間分解能以外の新たな次元を与えてくれることからハイパーの名前が付いています。ハイパースペクトルキューブを得られることからハイパースペクトルセンサーの由来になっています。
ハイパースペクトルキューブの高さや、縦、横の軸を上手に選択して可視化することで解析が可能になります。例えば、縦と横の点を選ぶと、高さ成分であるスペクトルの値を得ることができます。
ハイパースペクトルの可視化
ハイパースペクトルキューブを使ってデータを可視化して実装のイメージと、どのようなグラフが得られるのか確認していきましょう。
まずは、Wyvern Open Data Program のハイパースペクトル画像を使用します。
https://wyvern.space/open-data/

ワイバーンのデータは、「By Industry」 -> 「Agriculture」 -> 「wyvern_dragonette_001_20240802T063254_fe587307」 の COG (Cloud-Optimized GeoTIFF image) を使用します。制限に従うとダウンロードリンクから取得できます。波長分解能は 23バンドで緑波長から近赤外波長の範囲です。
GeoTiff形式のファイルなので画像情報と共に地理空間情報も付与されています。一般的なGISツール(QGIS, ArcGIS, ENVI など)で可視化が可能です。今回は、無料ツールであるQGISを使って見ていきます。QGISにドラッグアンドドロップで読み込みが可能です。
また、Tellus ではQGIS 対応の環境が提供されているサービスもあります。
https://www.tellusxdp.com/ja/dev/
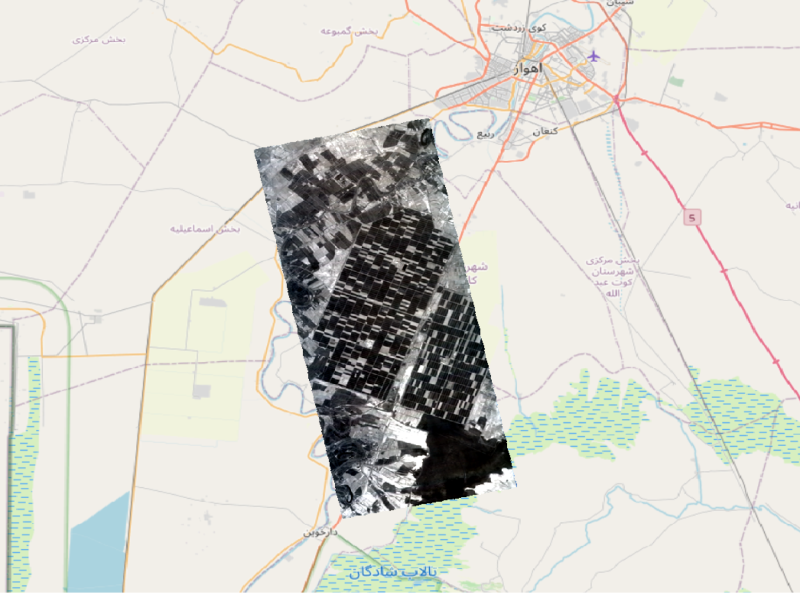
デフォルトでは、波長が短い、緑波長周辺のバンドが選択されています。
「プロパティ」 の「シンボロジ」のバンドの選択を見ていきます。
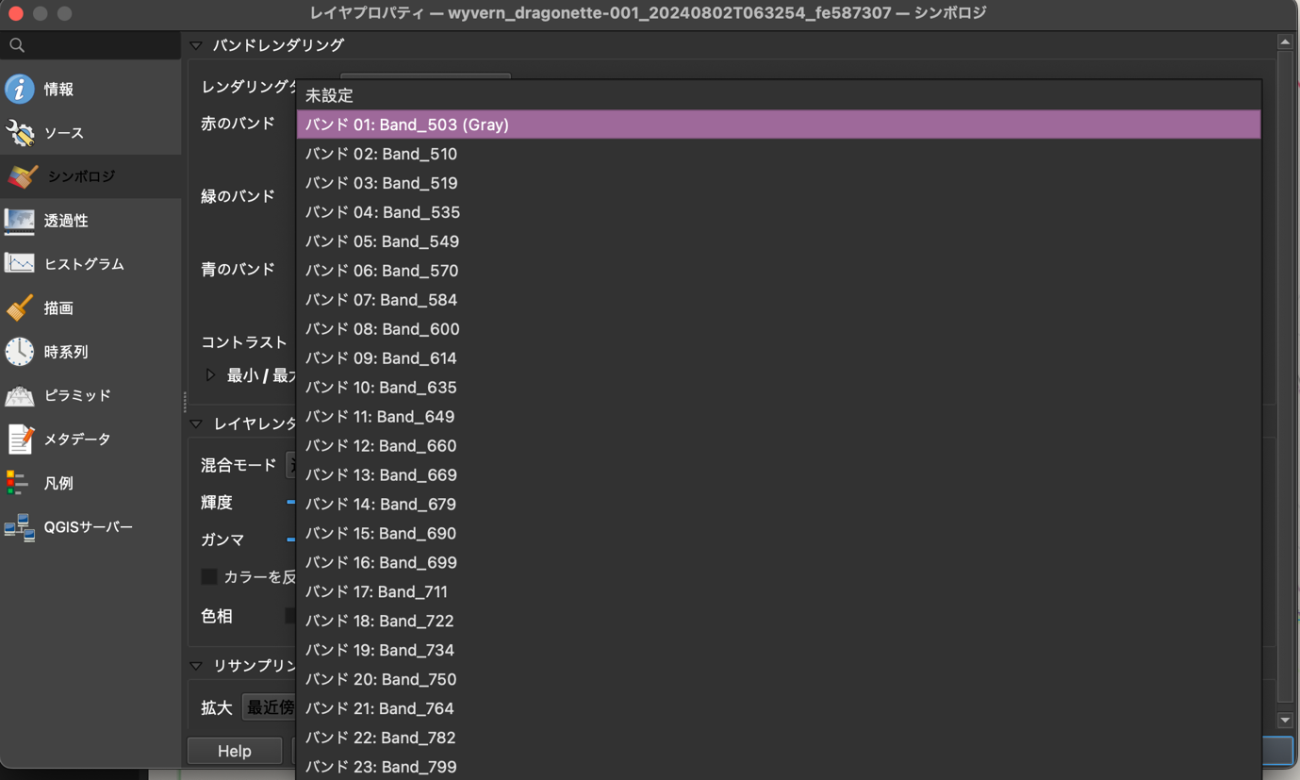
このようにたくさんのバンドを自由に選択して手軽に可視化が可能です。例えば、バンド[23, 13, 1]をそれぞれ[赤、緑、青]色に対応させて可視化して見ます。バンドの理由としては、フォルスカラー(False Color)になるように波長を選出しました。オリジナルのフォルスカラー画像のようなイメージです。
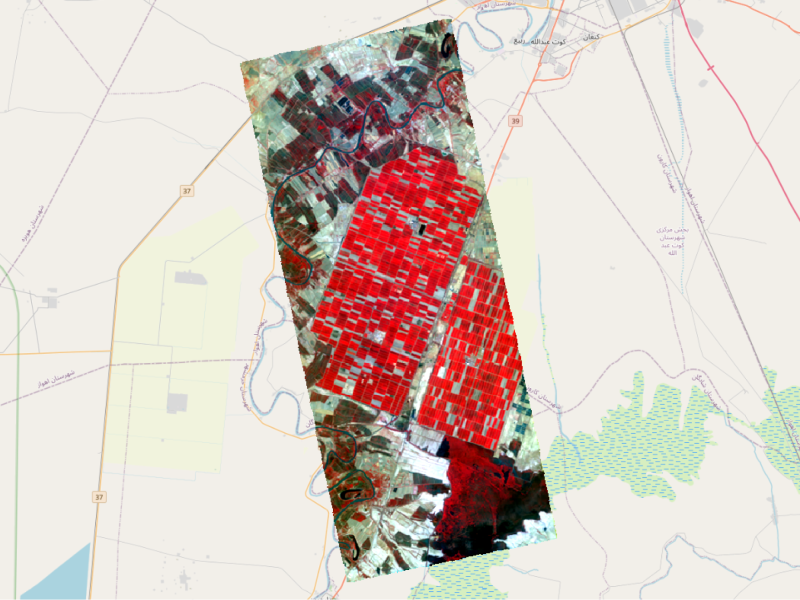
Credit : 2025 Wyvern Incorporated. All Rights Reserved.
フォルスカラー画像の説明は、以下がわかりやすいです。
課題に応じて変幻自在? 衛星データをブレンドして見えるモノ・コト #マンガでわかる衛星データ
フォルスカラー画像の利用例としては、以下などがあります。
衛星データから桜の開花検知によるお花見スポット探索の実装と3Dでの表現【MAXARの衛星データでやってみた】
ハイパースペクトルの基礎解析
QGISを使用して波長を合わせることで可視化する方法をご紹介しました。
しかしながら、ハイパースペクトルセンサーの特徴であるバンド数の多さが、可視化における課題となります。バンド数が100を超えるハイパースペクトルも多く存在します。
そこで、効率的なデータ処理のためにプログラムを用いた解析方法を知っておくことも重要です。
本記事では Python 言語での解析例もご紹介します。
QGISで利用したデータをPython でも解析していきましょう。 GeoTiff形式のハイパースペクトル画像を読み込みます。
filepath = 'data/wyvern_dragonette-001_20240802T063254_fe587307.tiff'
PATH_OUTPUT = os.path.join(os.path.dirname(filepath), 'output')
os.makedirs(PATH_OUTPUT, exist_ok=True)
hyper_cube = tifffile.imread(filepath)
hyper_cube.shape, hyper_cube.dtype
((11411, 7452, 23), dtype(‘float32’))
読み込んだデータの次元は縦が 11411、横が7452、バンドが23バンドです。
次に、ヒストグラムを表示してみます。
# plot histogram
plt.figure(figsize=(14, 3))
plt.title('Histogram of the hyperspectral cube [Linear scale]')
plt.hist(hyper_cube.flatten(), bins=200)
plt.yscale('linear')
plt.savefig(os.path.join(PATH_OUTPUT, 'histogram.png'))
plt.show();plt.clf();plt.close()
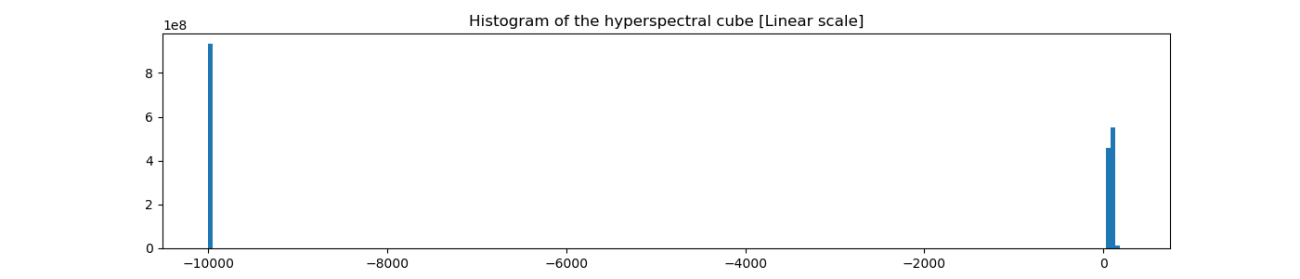
ヒストグラムを見ると、-10000 の値が大量に存在することがわかりました。衛星データではよくある事です。座標投影や観測時の欠損値が格納されていることが多いので、気をつけましょう。欠損値を取り除いてピクセルの頻度をログスケール(Log Scale)で表示してみます。
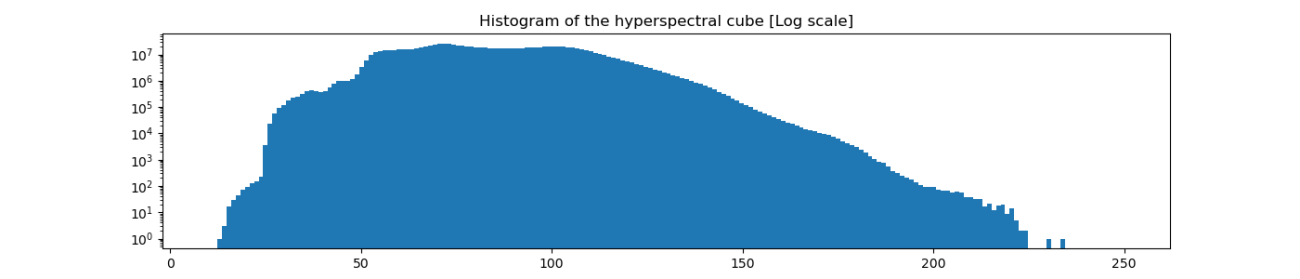
図から、反射強度の値は10〜250の間にあるようです。
1つ目のバンドを可視化してみましょう。
IDX_BAND = 0
plt.figure(figsize=(8,10), dpi=120, facecolor='w', edgecolor='k')
plt.title('Band {}'.format(IDX_BAND))
plt.imshow(hyper_cube[:,:,IDX_BAND], vmin=1)
plt.colorbar(shrink=0.6)
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'band_{}.png'.format(IDX_BAND)))
plt.show();plt.clf();plt.close()
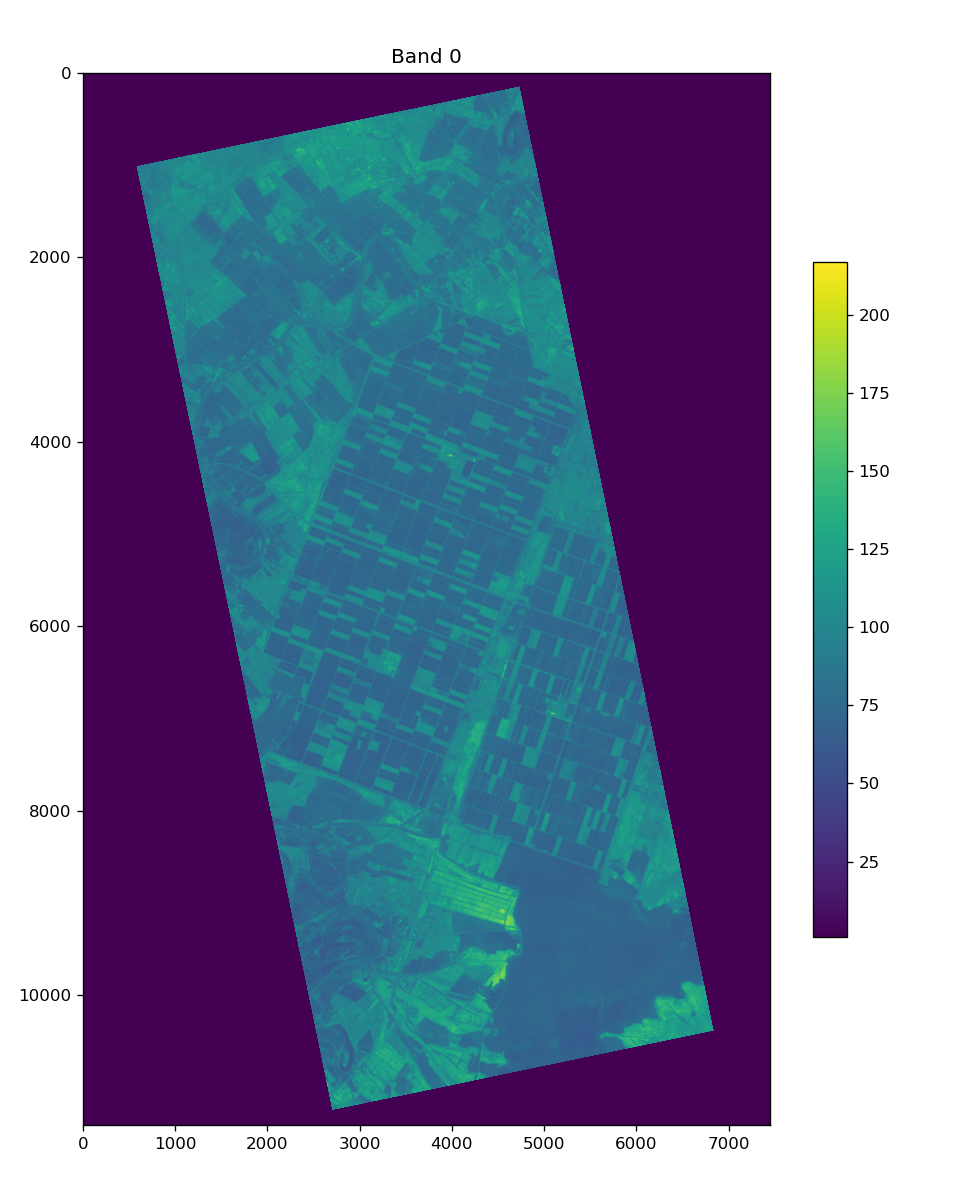
最後に全てのバンドを比較するために並べて可視化してみましょう。
plt.figure(figsize=(16 ,10), dpi=120, facecolor='w', edgecolor='k')
# band 23 -> 3 rows, 8 columns
for i in range(23):
plt.subplot(3, 8, i+1)
plt.title('Band {}'.format(i+1))
plt.imshow(hyper_cube[:,:,i], cmap='jet', vmin=1, vmax=200)
plt.colorbar(shrink=0.5)
plt.axis('off')
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'all_bands.png'))
plt.show();plt.clf();plt.close()
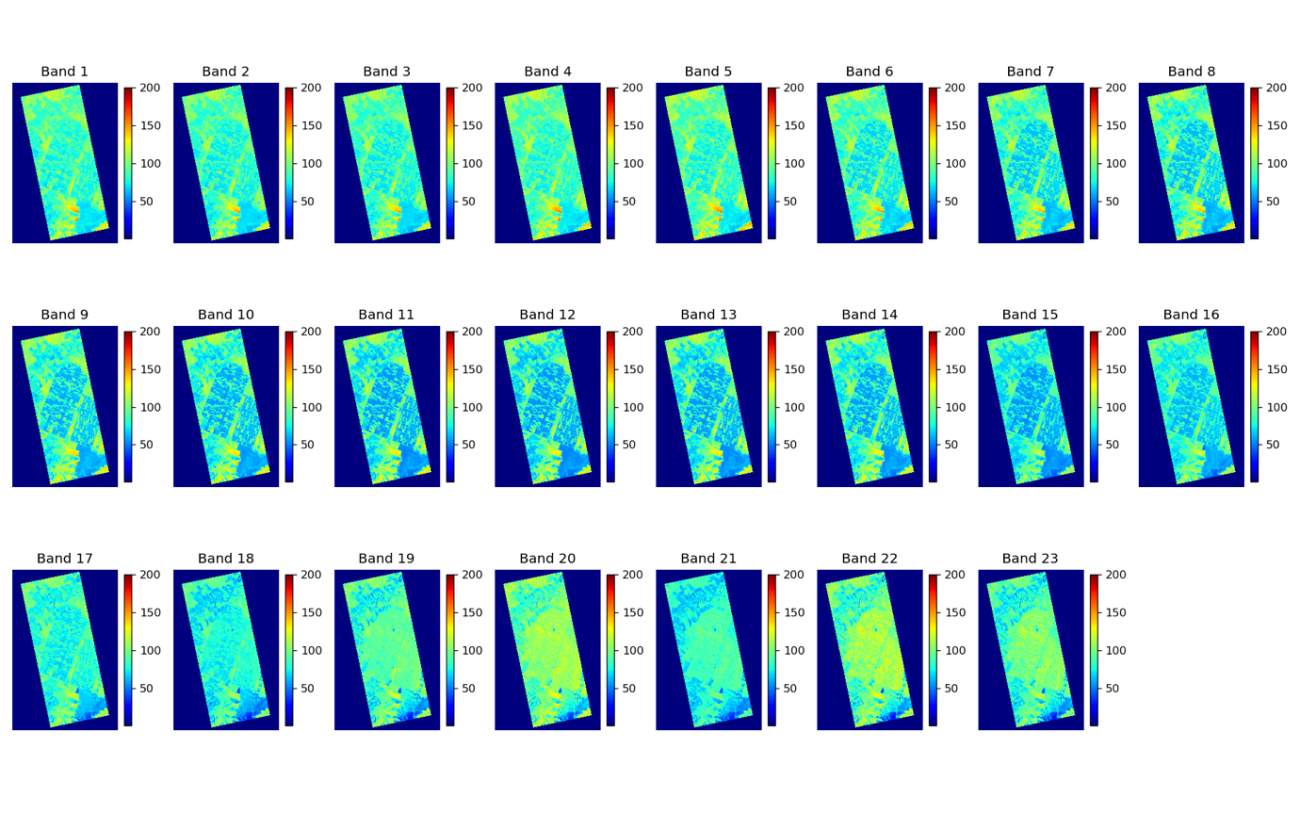
並べて比較することでバンドごとの反射強度の違いがわかりやすくなります。耕作地はバンド7〜16がはっきりと浮かび上がっていますね。
次に、耕作地について分析したい場合があったとします。以下のような耕作地のポリゴンの領域でくり抜きたい時の処理です。
{
"type": "FeatureCollection",
"name": "agriculture",
"crs": { "type": "name", "properties": { "name": "urn:ogc:def:crs:OGC:1.3:CRS84" } },
"features": [
{ "type": "Feature", "properties": { "id": null }, "geometry": { "type": "MultiPolygon", "coordinates": [ [ [ [ 48.471437177134156, 31.126019718132753 ], [ 48.519445374052474, 31.143664063292452 ], [ 48.560551453153316, 31.130004978005381 ], [ 48.562376805653713, 31.121766008763103 ], [ 48.571669509292072, 31.117930382506337 ], [ 48.568682568836884, 31.111679400177977 ], [ 48.582621624294411, 31.107559209500444 ], [ 48.586604211567987, 31.100170833672454 ], [ 48.501416742106834, 30.905509188132616 ], [ 48.413153116582251, 30.933578967753572 ], [ 48.422234818006544, 30.940255838558596 ], [ 48.43237095319617, 30.969144577774678 ], [ 48.416796064803144, 30.974276580653591 ], [ 48.418726836091544, 30.978359912715781 ], [ 48.408879902520752, 30.98156024004723 ], [ 48.408558107306028, 30.982884482032041 ], [ 48.471437177134156, 31.126019718132753 ] ] ] ] } }]
}QGISで可視化すると青色の領域がポリゴンです。
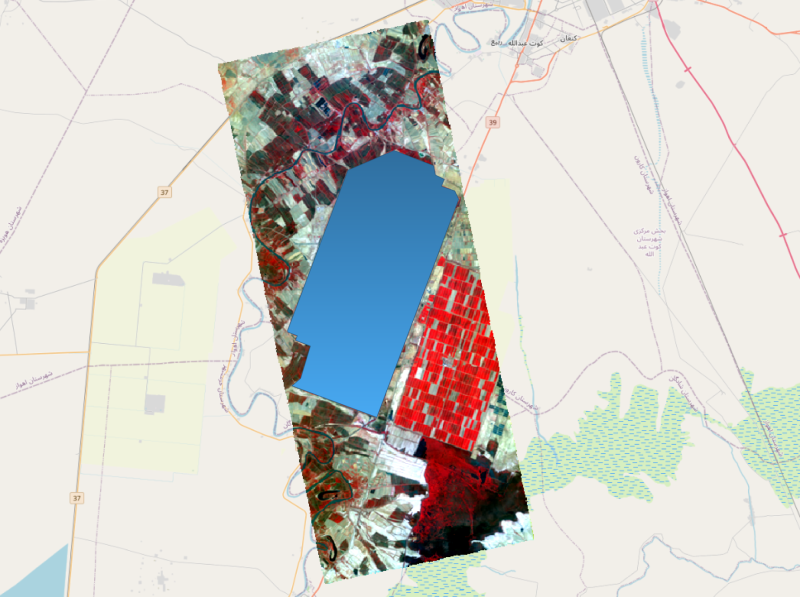
Credit : 2025 Wyvern Incorporated. All Rights Reserved.
他の光学画像やSAR画像と同じような実装で切り取ることが可能です。
def clip_raster_with_geojson(
raster_path,
geojson_path,
output_path,
nodata_value=np.nan):
"""
指定したGeoJSONのポリゴン領域で衛星画像をくり抜く。
Parameters:
raster_path (str): 入力の衛星画像ファイルパス (GeoTIFF)
geojson_path (str): GeoJSONファイルパス
output_path (str): 出力のクリップ後のGeoTIFFファイルパス
"""
# GeoJSON のポリゴンを読み込む
with open(geojson_path, 'r', encoding='utf-8') as f:
geojson_data = json.load(f)
# ポリゴンを抽出(複数のポリゴンがある場合も考慮)
polygons = [shape(feature['geometry']) for feature in geojson_data['features']]
# Raster を開いてマスク処理
with rasterio.open(raster_path) as src:
out_image, out_transform = rasterio.mask.mask(src, polygons, crop=True)
out_meta = src.meta.copy()
# メタデータを更新
out_meta.update({
"driver": "GTiff",
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform,
"nodata": nodata_value
})
# 出力ファイルを保存
with rasterio.open(output_path, "w", **out_meta) as dest:
dest.write(out_image)
# 使用例
clip_raster_with_geojson(filepath, "data/agriculture.geojson",
f"{PATH_OUTPUT}/croped_agriculture.tif")
hyper_cube_agriculture = tifffile.imread(f"{PATH_OUTPUT}/croped_agriculture.tif")
# Plot the first band
IDX_BAND = 0
plt.figure(figsize=(8,10), dpi=120, facecolor='w', edgecolor='k')
plt.title('Band {}'.format(IDX_BAND))
plt.imshow(hyper_cube_agriculture[:,:,IDX_BAND], vmin=1)
plt.colorbar(shrink=0.6)
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'band_{}_agriculture.png'.format(IDX_BAND)))
plt.show();plt.clf();plt.close()
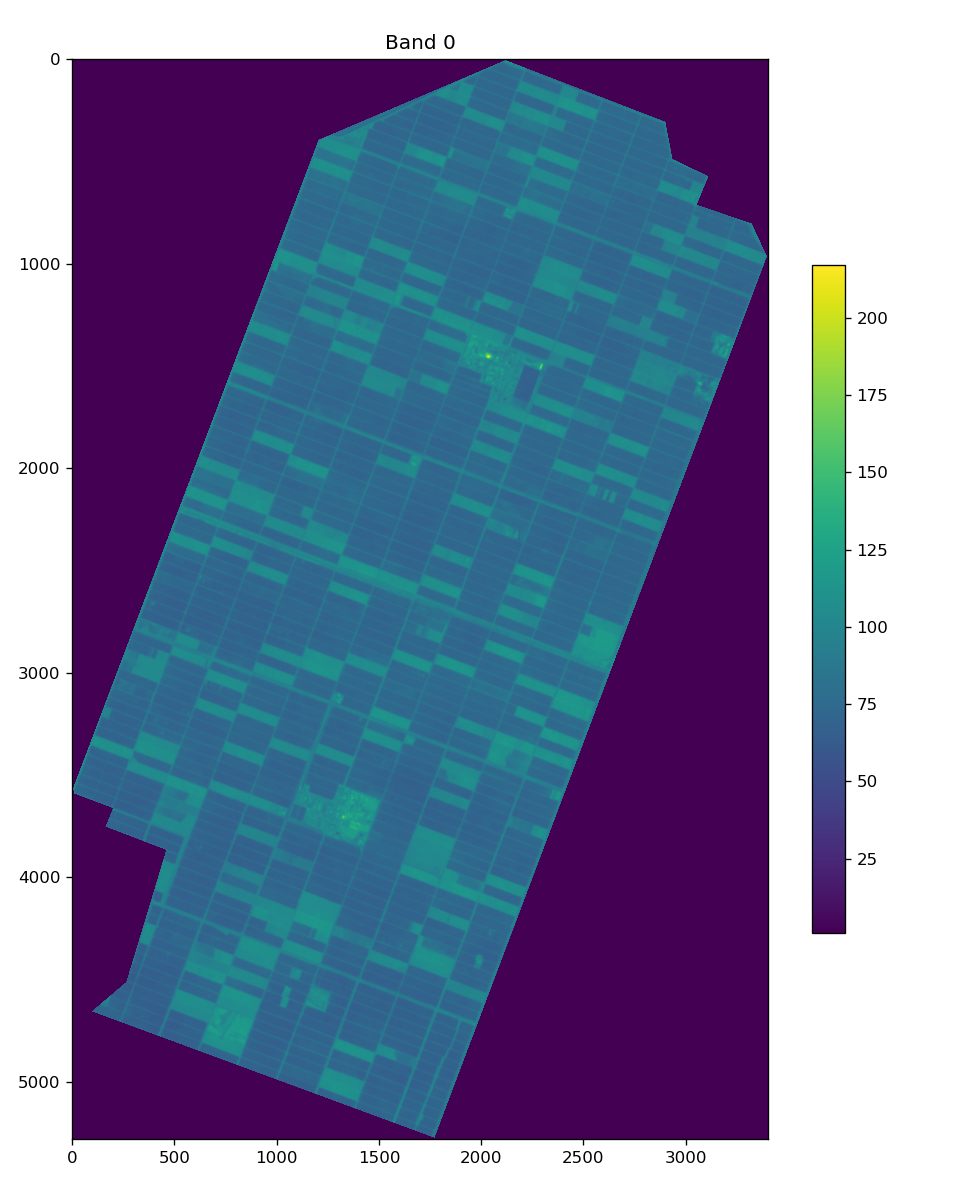
Credit : 2025 Wyvern Incorporated. All Rights Reserved.
図のように耕作地のみを解析できるようになりました。ハイパースペクトルデータも高い波長分解能を維持したまま地理空間的に制限した部分のみの解析を行うことができます。
最後にスペクトルの可視化を行います。ハイパースペクトルキューブの地理空間的な縦横を指定してそのピクセルの高さ成分であるスペクトルを波長ごとに可視化します。今回のデータでは、23バンドを可視化します。可視化する点はP1とP2の2つです。
P1 = (4100, 3600)
P2 = (10500, 5200)
POINT_1_SPECTRAL = hyper_cube[P1[0], P1[1], :]
POINT_2_SPECTRAL = hyper_cube[P2[0], P2[1], :]
# Plot the spectral signature
plt.figure(figsize=(14, 3), dpi=120, facecolor='w', edgecolor='k')
plt.title('Hyper Spectral of two points')
plt.plot(POINT_1_SPECTRAL, label='Point 1')
plt.plot(POINT_2_SPECTRAL, label='Point 2')
plt.legend()
plt.grid()
plt.savefig(os.path.join(PATH_OUTPUT, 'spectral_signature.png'))
plt.show();plt.clf();plt.close()
plt.figure(figsize=(8,10), dpi=100, facecolor='w', edgecolor='k')
plt.title('Band 20')
plt.imshow(hyper_cube[:,:,20], vmin=1)
plt.scatter(*P1[::-1], c='r', s=100, label='Point 1')
plt.scatter(*P2[::-1], c='b', s=100, label='Point 2')
plt.legend()
plt.tight_layout()
plt.savefig(os.path.join(PATH_OUTPUT, 'band_20_point.png'))
plt.show();plt.clf();plt.close()
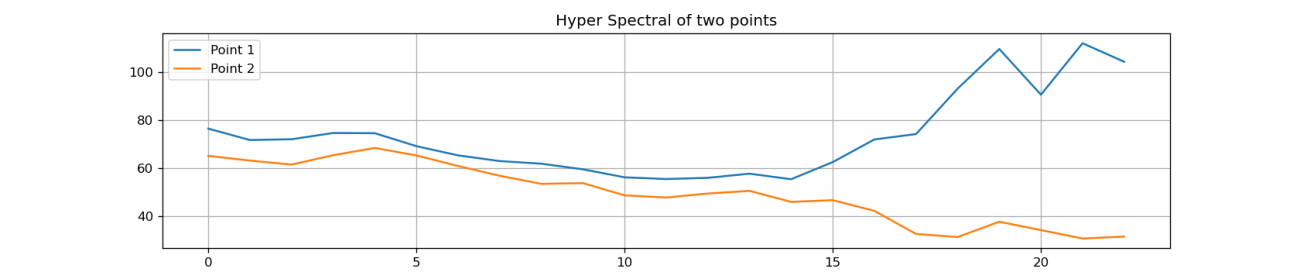
図の折れ線グラフは、縦が反射強度で横がバンドの番号です。図からバンド1〜14までは似たような反射強度を示していますが、バンド15〜23では異なる振る舞いをしています。
地理空間的な位置も可視化することをオススメします。波長分解能だけではなく、地理空間的な情報により総合的な判断もできるようになるからです。
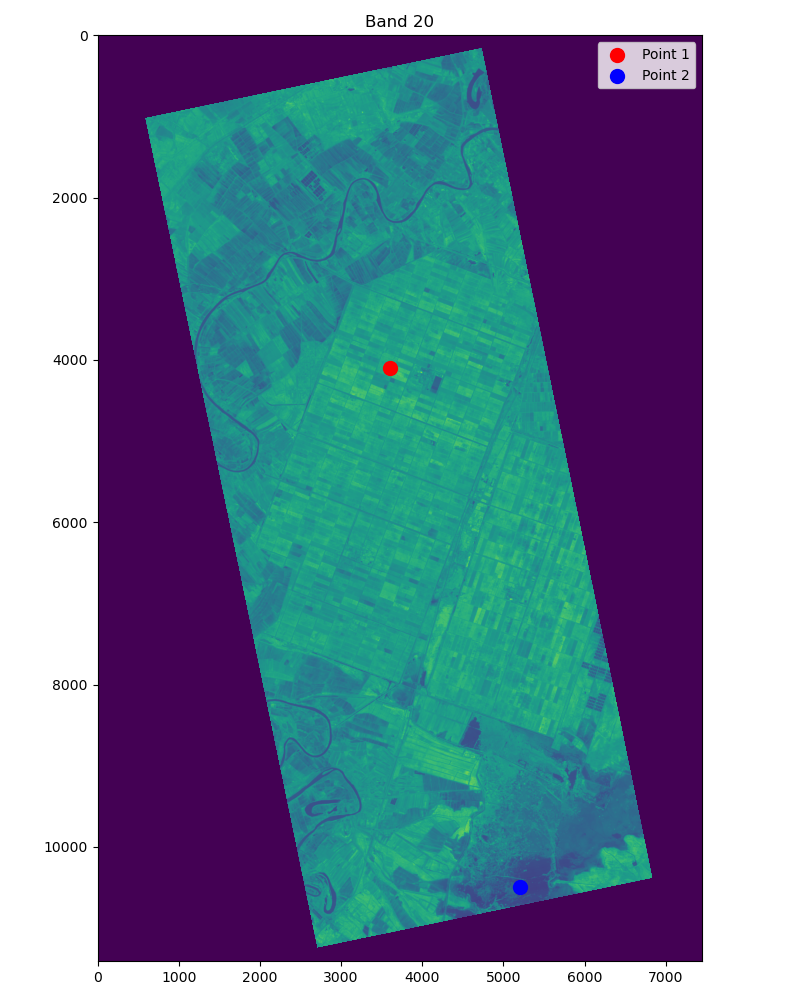
Credit : 2025 Wyvern Incorporated. All Rights Reserved.
赤色で示したPoint 1は耕作地であり、青色で示したPoint2は湿地帯のようなところでした。
ディープラーニングを用いたハイパースペクトル解析
近年では、衛星画像をディープラーニングの学習データに使用することも一般的になってきました。ハイパースペクトルデータをディープラーニングのモデルの入力にする解析例を、最後にご紹介します。
よく使用されるコンボリューショナルニューラルネットワーク(Convolutional Neural Network; CNN)の実装をします。ハイパースペクトルの特徴を生かしつつ、画像の空間的なピクセル情報を維持するにはチャンネル方向の入力を増やす方法をオススメします。具体的には、「in_chans=23」の部分です。
# create a model
cnn = timm.create_model('resnet18', pretrained=False, in_chans=23,)
print(cnn)
oputputs = cnn(inputs)[0]
print(f"\n Model Output Class: {oputputs.shape}")
# show graph
model_graph = draw_graph(cnn, input_size=inputs.shape, expand_nested=False)
display(model_graph.visual_graph)
# save graph
model_graph.visual_graph.render(filename=f'{PATH_OUTPUT}/CNN_Graph', format='png', cleanup=True)
ResNet(
(conv1): Conv2d(23, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act1): ReLU(inplace=True)
(maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
(layer1): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
)
(1): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
)
)
(layer2): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
)
)
(layer3): Sequential(
(0): BasicBlock(
(conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
)
)
(layer4): Sequential(
(0): BasicBlock(
(conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(drop_block): Identity()
(act1): ReLU(inplace=True)
(aa): Identity()
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(act2): ReLU(inplace=True)
)
)
(global_pool): SelectAdaptivePool2d (pool_type=avg, flatten=Flatten(start_dim=1, end_dim=-1))
(fc): Linear(in_features=512, out_features=1000, bias=True)
)
Model Output Class: torch.Size([1000])

レイヤーのConv1の入力サイズが23バンドのモデルが作成できています。
セグメンテーションで良く使用されるUNetでの実装は以下です。「in_channels=23」の部分で変更しています。
# create a model
unet = smp.Unet(
encoder_name="resnet18",
encoder_weights=None,
in_channels=23,
classes=10,
)
print(unet)
outputs = unet(inputs)[0]
print(f"\n Model Output Class: {outputs.shape}")
# show graph
model_graph = draw_graph(cnn, input_size=inputs.shape, expand_nested=True)
display(model_graph.visual_graph)
# save graph
model_graph.visual_graph.render(filename=f'{PATH_OUTPUT}/UNet_Graph', format='png', cleanup=True)

ハイパースペクトル特有の解析
基礎的な解析がわかったところでハイパースペクトルを生かした解析方法をご紹介します。まずは、ハイパースペクトルキューブの可視化です。キューブのような3D空間の操作をすることで見えるようになるとが多々あるからです。
PACTH = 512
RESIZE = 128
PATH_OUTPUT = os.path.join(os.path.dirname(filepath), 'output')
os.makedirs(PATH_OUTPUT, exist_ok=True)
hyper_cube = tifffile.imread(filepath)
print(hyper_cube.shape, hyper_cube.dtype)
hyper_cube_patch = hyper_cube[4000:4000+PACTH, 2000:2000+PACTH, :]
np.save(os.path.join(PATH_OUTPUT, f'hypercube_patch_{PACTH}.npy'), hyper_cube_patch)
hyper_cube_patch = np.load(os.path.join(PATH_OUTPUT, f'hypercube_patch_{PACTH}.npy'))
hyper_cube_patch = cv2.resize(hyper_cube_patch, (RESIZE, RESIZE), interpolation=cv2.INTER_CUBIC)
# stack blanck z axis
hyper_cube_patch = np.concatenate([hyper_cube_patch, np.zeros((RESIZE, RESIZE, 1))], axis=2)
H, W, B = hyper_cube_patch.shape
X, Y, Z = np.mgrid[0:H, 0:W, 0:B]
img_rgb = hyper_cube_patch[:, :, [2]]
print(f'Drawing hypercube patch with shape {hyper_cube_patch.shape}')
# plot 3D volume
fig = go.Figure(data=go.Volume(
x=X.flatten(),
y=Y.flatten(),
z=Z.flatten(),
value=hyper_cube_patch.flatten(),
opacity=0.2, # needs to be small to see through all surfaces
surface_count=17, # needs to be a large number for good volume rendering
colorscale="Jet", # カラーマップ Viridis, Cividis, Inferno, Magma, Plasma, Turbo, Jet
))
fig.add_trace(go.Surface(
x=np.arange(H),
y=np.arange(W),
z=np.full((H, W), B), # Z=B-1 の位置に配置
surfacecolor=img_rgb, # グレースケール画像を適用
colorscale="Viridis", # 画像のカラーマップ
opacity=0.9, # needs to be small to see through all surfaces
))
# 軸の設定 & 高解像度
fig.update_layout(
title="Hyperspectral Data 3D Visualization",
width=1200, # 高解像度用にサイズアップ
height=800,
scene=dict(
xaxis_title="Height [Spacial]",
yaxis_title="Width [Spacial]",
zaxis_title="Spectral [Band]",
aspectmode="cube"
)
)
fig.show();
# save image
fig.write_image(os.path.join(PATH_OUTPUT, 'hypercube_patch.png'), scale=2)
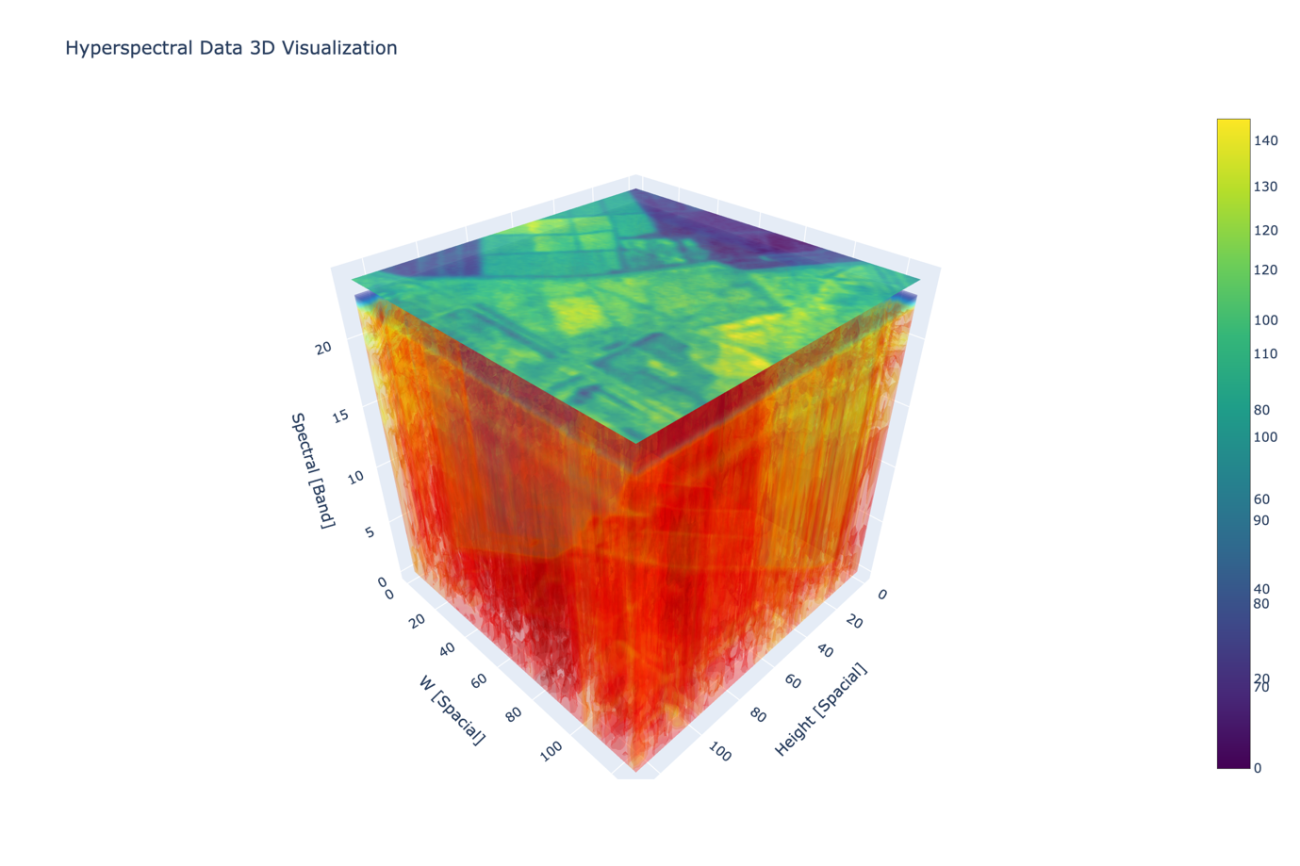
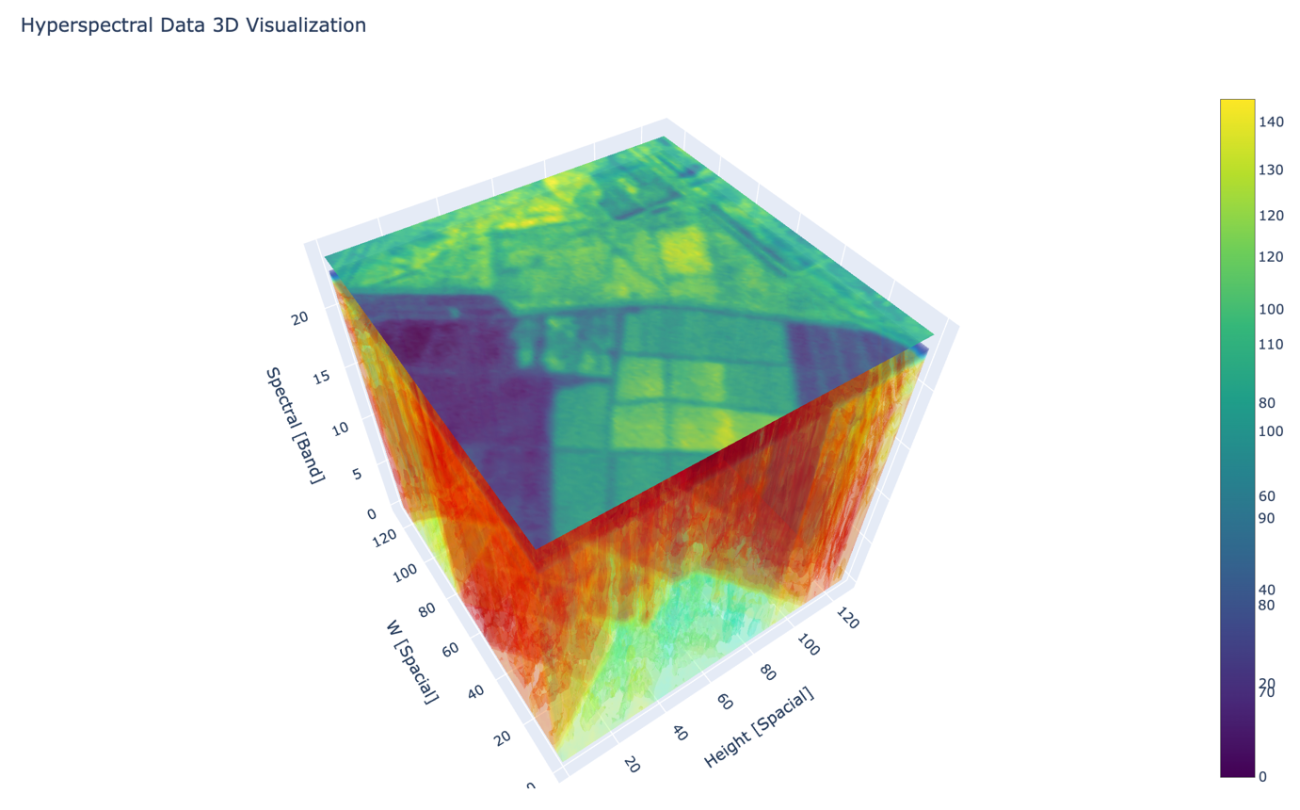
3D操作をすることで滑らかに波長分解能と空間分解能を移動することが可能になります。
その際には、ハイパースペクトルキューブの一番上にくるバンドとして、耕作地などの地物がわかりやすいバンドを選択すると良いでしょう。
一見同じに見える農地でもハイパースペクトルを確認すると強度が異なっていたります。下図のように赤色の強い反射をする農地もあれば、緑色の低い値しか反射しない農地もあります。このような違いは波長分解能があるからこその違いが見えているといえるでしょう。

また、観測したい領域が点の場合はキューブ状ではなく、線で可視化することも有効です。
filepath = 'data/wyvern_dragonette-001_20240802T063254_fe587307.tiff'
PATH_OUTPUT = os.path.join(os.path.dirname(filepath), 'output')
os.makedirs(PATH_OUTPUT, exist_ok=True)
print('Loading hypercube...')
P1 = (1000, 2000)
P2 = (1000, 3000)
P3 = (2000, 3000)
P4 = (2000, 2000)
P5 = (1500, 2500)
P6 = (1500, 1500)
hyper_cube = tifffile.imread(filepath)
print(hyper_cube.shape, hyper_cube.dtype)
NUM_SPECTRAL = hyper_cube.shape[2]
spec_p1 = np.array(hyper_cube[P1[0], P1[1], :])
spec_p2 = np.array(hyper_cube[P2[0], P2[1], :])
spec_p3 = np.array(hyper_cube[P3[0], P3[1], :])
X1 = np.stack([np.array([P1[0],])]*NUM_SPECTRAL, axis=0)
Y1 = np.stack([np.array([P1[1],])]*NUM_SPECTRAL, axis=0)
Z1 = np.stack([np.arange(hyper_cube.shape[2])]*NUM_SPECTRAL, axis=0)
X2 = np.stack([np.array([P2[0],])]*NUM_SPECTRAL, axis=0)
Y2 = np.stack([np.array([P2[1],])]*NUM_SPECTRAL, axis=0)
Z2 = np.stack([np.arange(hyper_cube.shape[2])]*NUM_SPECTRAL, axis=0)
X3 = np.stack([np.array([P3[0],])]*NUM_SPECTRAL, axis=0)
Y3 = np.stack([np.array([P3[1],])]*NUM_SPECTRAL, axis=0)
Z3 = np.stack([np.arange(hyper_cube.shape[2])]*NUM_SPECTRAL, axis=0)
X4 = np.stack([np.array([P4[0],])]*NUM_SPECTRAL, axis=0)
Y4 = np.stack([np.array([P4[1],])]*NUM_SPECTRAL, axis=0)
Z4 = np.stack([np.arange(hyper_cube.shape[2])]*NUM_SPECTRAL, axis=0)
X5 = np.stack([np.array([P5[0],])]*NUM_SPECTRAL, axis=0)
Y5 = np.stack([np.array([P5[1],])]*NUM_SPECTRAL, axis=0)
Z5 = np.stack([np.arange(hyper_cube.shape[2])]*NUM_SPECTRAL, axis=0)
X6 = np.stack([np.array([P6[0],])]*NUM_SPECTRAL, axis=0)
Y6 = np.stack([np.array([P6[1],])]*NUM_SPECTRAL, axis=0)
Z6 = np.stack([np.arange(hyper_cube.shape[2])]*NUM_SPECTRAL, axis=0)
# plot 3D volume
fig = go.Figure(
data=[
go.Scatter3d(
x=X1.flatten(), y=Y1.flatten(), z=spec_p1.flatten(),
marker=dict(
size=8,
color=spec_p1.flatten(),
colorscale='Jet',
),
line=dict(
color='darkblue',
width=4
)
),
go.Scatter3d(
x=X2.flatten(), y=Y2.flatten(), z=spec_p2.flatten(),
marker=dict(
size=8,
color=spec_p2.flatten(),
colorscale='Jet',
),
line=dict(
color='darkblue',
width=4
),
),
go.Scatter3d(
x=X3.flatten(), y=Y3.flatten(), z=spec_p3.flatten(),
marker=dict(
size=8,
color=spec_p3.flatten(),
colorscale='Jet',
),
line=dict(
color='darkblue',
width=4
),
),
go.Scatter3d(
x=X4.flatten(), y=Y4.flatten(), z=hyper_cube[P4[0], P4[1], :],
marker=dict(
size=8,
color=hyper_cube[P4[0], P4[1], :],
colorscale='Jet',
),
line=dict(
color='darkblue',
width=4
),
),
go.Scatter3d(
x=X5.flatten(), y=Y5.flatten(), z=hyper_cube[P5[0], P5[1], :],
marker=dict(
size=8,
color=hyper_cube[P5[0], P5[1], :],
colorscale='Jet',
),
line=dict(
color='darkblue',
width=4
),
),
go.Scatter3d(
x=X6.flatten(), y=Y6.flatten(), z=hyper_cube[P6[0], P6[1], :],
marker=dict(
size=8,
color=hyper_cube[P6[0], P6[1], :],
colorscale='Jet',
),
line=dict(
color='darkblue',
width=4
),
),
]
)
# 軸の設定 & 高解像度
fig.update_layout(
title="Hyperspectral Data 3D Visualization",
width=1200, # 高解像度用にサイズアップ
height=800,
scene=dict(
xaxis_title="Height [Spacial]",
yaxis_title="Width [Spacial]",
zaxis_title="Spectral [Band]",
aspectmode="cube"
)
)
fig.show();
# save image
fig.write_image(os.path.join(PATH_OUTPUT, 'hypercube_spec_line.png'), scale=2)
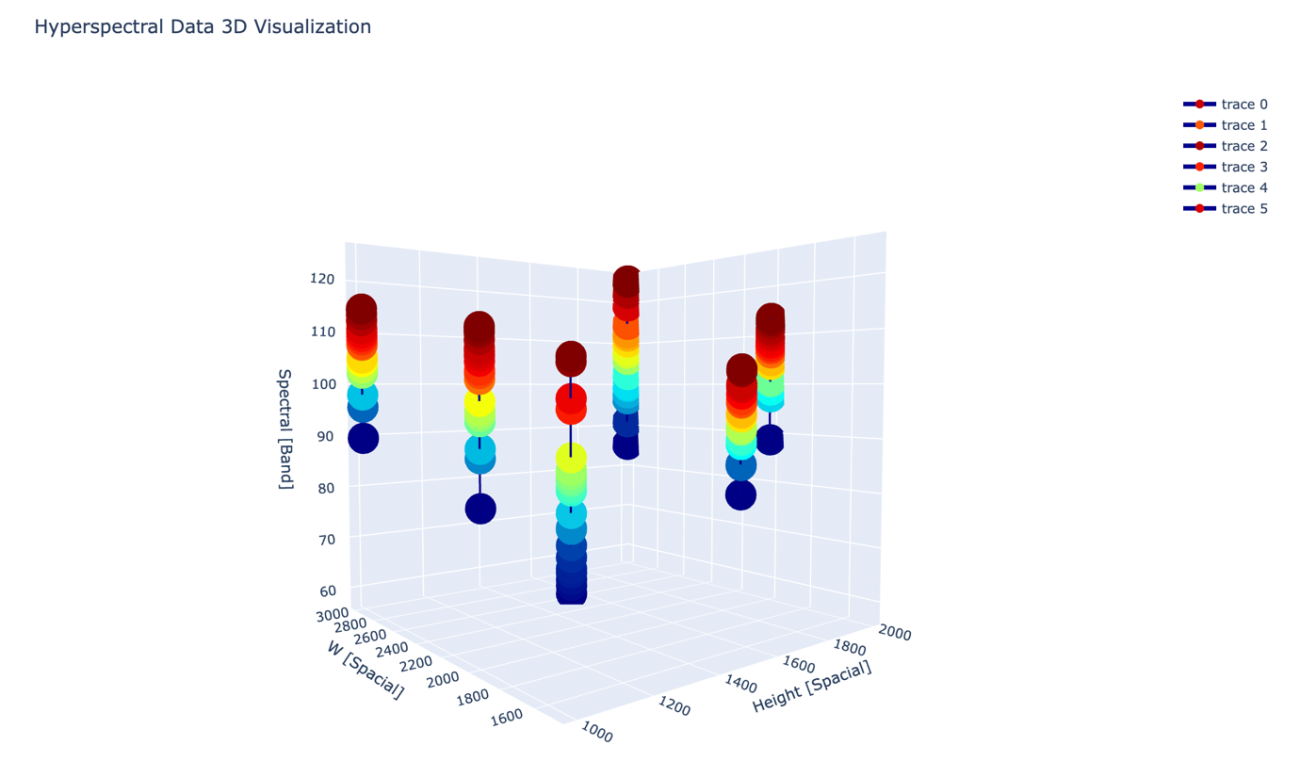
図の縦と横が空間的な軸です。そして、図の高さがバンドごとの反射強度を示しています。バンドごとの値の広がりなどから固有のスペクトルの振る舞いを得るヒントになるでしょう。
今回は基礎から内部を理解しやすいように、3D可視化の Python ライブラリーであるPlotly を使用して基礎からコードを書きました。
Python の可視化ライブラリーは matplotlib や PyVist など様々あります。可視化したい方法に合わせて有効なライブラリーを使用しましょう。
https://matplotlib.org/
https://docs.pyvista.org/
また、Python ライブラリーでは HyperCoast というハイパースペクトル解析専用の沿岸環境の分析、可視化ツールも存在します。目的に合わせて簡単に解析できる OSS も増えています。
DESISの解析例
では、次にもっと波長分解能が高い DESISのデータを扱っていきます。
NASAのDESIS(DLR Earth Sensing Imaging Spectrometer)は、ドイツ航空宇宙センター(DLR)とAirbus Defence and Spaceによって開発されたハイパースペクトルイメージングセンサーです。
このセンサーは2018年に国際宇宙ステーション(ISS)のMUSES(Multi-User System for Earth Sensing)プラットフォームに搭載され、地球観測のために運用されています。ISSに搭載されている利点として、静止衛星や極軌道衛星とは異なり、特定の地域を短期間で繰り返し観測できる点が挙げられます。
このため、時間変化のある現象のモニタリングに適しています。例えば、作物の成長状況の追跡や森林の健康診断、海洋の藻類ブルーム(赤潮など)の監視、災害発生後の影響評価に活用されています。また、DESISのデータはAirbusが管理し、商業利用が可能な形で提供されています。これにより、研究機関や企業がハイパースペクトルデータを活用し、新たな解析手法の開発や実用化に取り組むことができます。
DESIS のデータは NASA の Earth Data から取得が可能です。データを読み込んでバンド数などのハイパーキューブの情報を取得します。
hypercube = dataset["reflectance"]
wavelents = dataset["wavelength"]
print(hypercube.shape)
(229, 332, 235)
全体で 235バンドという高い波長分解能を持っています。滑らかなスペクトルを可視化していきます。その前に、スペクトルを測る点と DESIS の画像を可視化します。
P1 = (220, 200)
P2 = (9, 98)
P3 = (100, 140)
img = hypercube[:, :, [129, 76 , 6]]
# nomalize by band
img = (img - img.min(axis=(0, 1 ))) / (img.max(axis=(0, 1))- img.min(axis=(0, 1 )))
img = np.clip(img, 0, 1)
img = (img * 255).astype(np.uint8)
# plot
plt.figure(figsize=(12, 8), dpi=120, facecolor="w", edgecolor="k")
plt.imshow(img, aspect="auto")
plt.scatter(*P1[::-1], color="c", s=100, label="P1", marker="x")
plt.scatter(*P2[::-1], color="b", s=100, label="P2", marker="x")
plt.scatter(*P3[::-1], color="y", s=100, label="P3", marker="x")
plt.title("Color Image")
plt.legend()
plt.tight_layout()
plt.savefig("data/output/desis_rgb.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()

P1〜P3の点のスペクトルを可視化していきます。
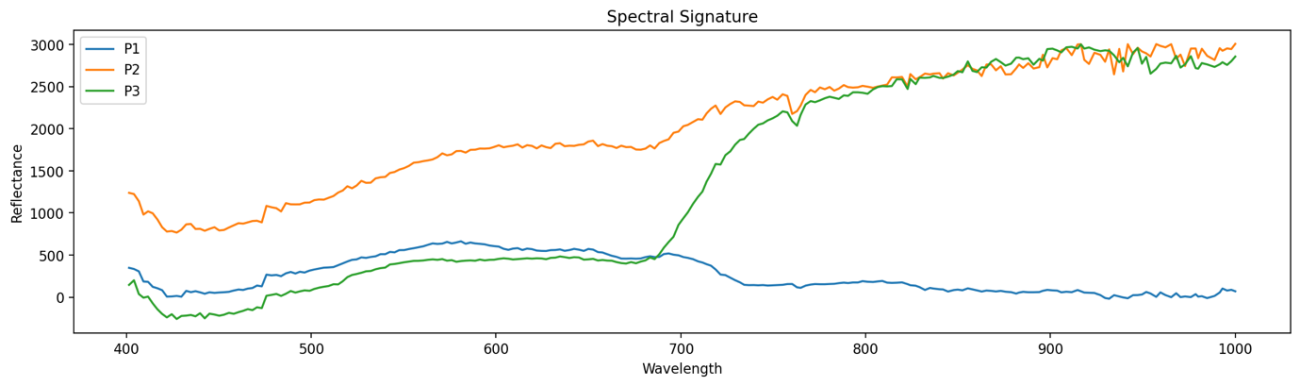
空間的にも異なりそうな3点を設定しました。スペクトルもそれぞれによって異なる値の変化を表しています。
これらの違いを部分的最小二乗回帰(Partial Least Squares Regression; PLS)という多変量解析の手法を使用して分類していきます。ハイパースペクトルは情報が多く豊富な代わりに、それぞれのスペクトルを整理して解析するには時間がかかってしまいます。そこで多くの情報を整理するのに適した多変量解析の手法が有効になります。
部分的最小二乗回帰は、たくさんの変数(スペクトル)からはっきりと違いがわかる変数を合成して線形回帰する方法です。一般的な線形回帰と異なり全ての変数に対して計算するのではなく、効果的な変数のみを使用します。
データからスペクトルの整理に活用でき、ノイズに強いというメリットがあります。
PLSを用いた回帰モデルを使って、指定した点が海かどうかを判定してみます。
sample = 4
P1_S = np.array(hypercube[P1[0]-sample//2:P1[0]+sample//2, P1[1]-sample//2:P1[1]+sample//2, :]).reshape(sample**2, -1)
P2_S = np.array(hypercube[P2[0]-sample//2:P2[0]+sample//2, P2[1]-sample//2:P2[1]+sample//2, :]).reshape(sample**2, -1)
P3_S = np.array(hypercube[P3[0]-sample//2:P3[0]+sample//2, P3[1]-sample//2:P3[1]+sample//2, :]).reshape(sample**2, -1)
学習データは P1〜P3周辺の4点です。
from sklearn.cross_decomposition import PLSRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X_train = np.concatenate([P1_S, P2_S, P3_S])
# 海域: 0, 陸域: 1
Y_train = np.array([0]*len(P1_S) + [1]*len(P2_S) + [1]*len(P3_S))
# PLS回帰モデルの学習
n_components = 2 ** 3 # PLSの成分数
pls = PLSRegression(n_components=n_components)
pls.fit(X_train, Y_train)
学習が完了したのでテストデータの点を用意します。
P4 = (100, 100)
P5 = (200, 300)
# plot
plt.figure(figsize=(10, 6), dpi=100, facecolor="w", edgecolor="k")
plt.imshow(img, aspect="auto")
plt.scatter(*P4[::-1], color="w", s=100, label="P4", marker="x")
plt.scatter(*P5[::-1], color="r", s=100, label="P5", marker="x")
plt.title("Color Image")
plt.legend()
plt.tight_layout()
plt.savefig("data/output/desis_rgb_p4.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()

この点の周囲4点をテストデータとします。
X_test_4 = np.array(hypercube[P4[0]-sample//2:P4[0]+sample//2, P4[1]-sample//2:P4[1]+sample//2, :]).reshape(sample**2, -1)
Y_test_4 = [1] * sample**2
X_test_5 = np.array(hypercube[P5[0]-sample//2:P5[0]+sample//2, P5[1]-sample//2:P5[1]+sample//2, :]).reshape(sample**2, -1)
Y_test_5 = [0] * sample**2
Y_sample = np.arange(sample**2)
# 予測
Y_pred_4 = pls.predict(X_test_4)
Y_pred_5 = pls.predict(X_test_5)
# 評価
mse_4 = mean_squared_error(Y_test_4, Y_pred_4)
print(f"Point No.4 --> Mean Squared Error: {mse_4:.4f}")
mse_5 = mean_squared_error(Y_test_5, Y_pred_5)
print(f"Point No.5 --> Mean Squared Error: {mse_5:.4f}")
# 結果の可視化
plt.figure(figsize=(12, 4), dpi=100, facecolor="w", edgecolor="k")
plt.scatter(Y_sample, Y_pred_4, color="b", label="P4")
plt.scatter(Y_sample, Y_pred_5, color="r", label="P5")
plt.xlabel("Sample Index")
plt.ylabel("Predicted Values")
plt.legend()
plt.title("PLS Regression: Actual vs Predicted")
plt.tight_layout()
plt.savefig("data/output/desis_pls.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()
Point No.4 –> Mean Squared Error: 0.0386
Point No.5 –> Mean Squared Error: 0.0002
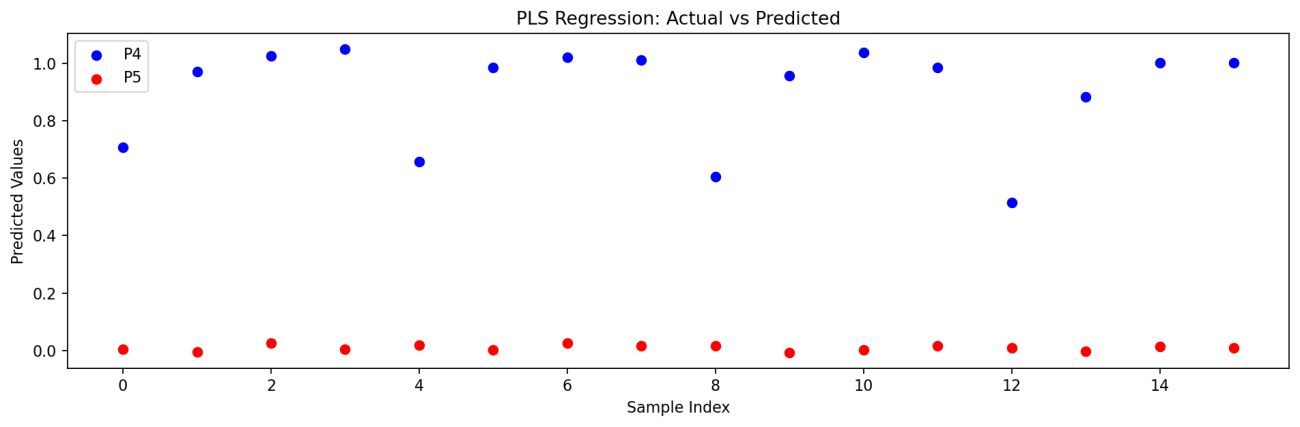
定量評価をMSE(平均二乗誤差)で算出した結果ではかなり低くなっています。予測値に関しても2値分類確率も良さそうなのではないでしょうか
# Explained variance ratio for each component
explained_variance = np.var(pls.x_scores_, axis=0) / np.sum(np.var(pls.x_scores_, axis=0))
# Plot: Contribution ratio of each component
plt.figure(figsize=(12, 4), dpi=100, facecolor="w", edgecolor="k")
plt.bar(range(1, len(explained_variance) + 1), explained_variance * 100, color='skyblue', edgecolor='black')
plt.xlabel("Component")
plt.ylabel("Explained Variance (%)")
plt.title("Explained Variance by Component")
plt.xticks(range(1, len(explained_variance) + 1))
plt.savefig(os.path.join("data", "output", "pls_explained_variance.png"), dpi=160, bbox_inches="tight")
plt.show()
wavelents = np.array(wavelents)
# Feature importance in PLS components (weights)
weights_df = pd.DataFrame(pls.x_weights_,
index=wavelents,
columns=['Component {}'.format(i) for i in range(1, n_components + 1)])
# Plot: Feature importance
weights_df.plot(kind='bar', figsize=(16, 6))
plt.xlabel("Wavelength")
plt.ylabel("Weight")
plt.title("Wavelength Importance in PLS Components")
plt.xticks([])
plt.legend(title="PLS Component")
plt.grid()
plt.savefig(os.path.join("data", "output", "pls_feature_importance.png"), dpi=160, bbox_inches="tight")
plt.show()
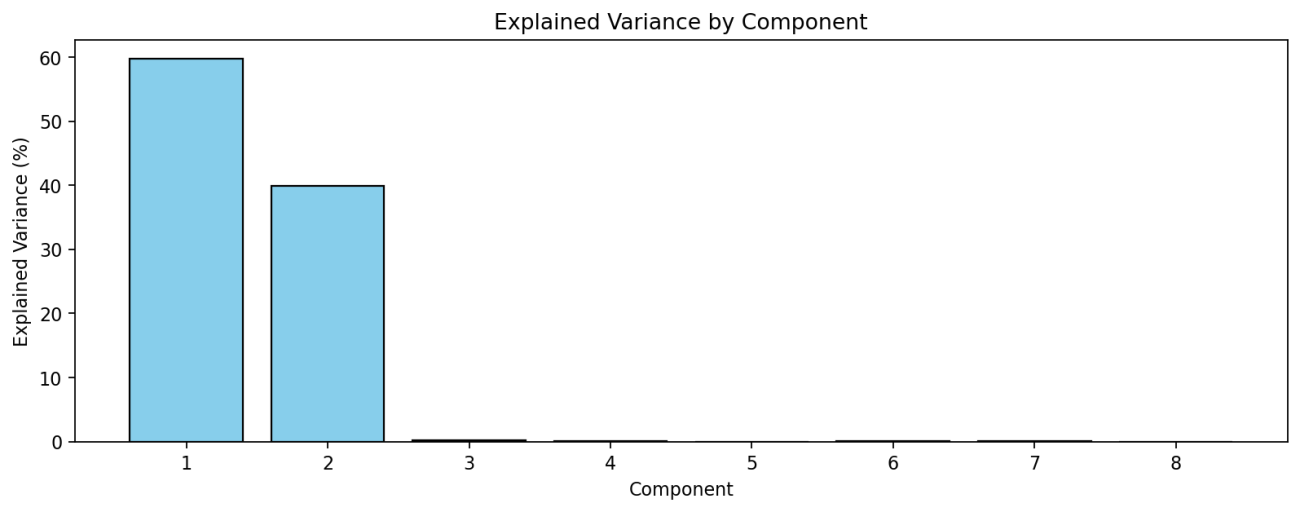
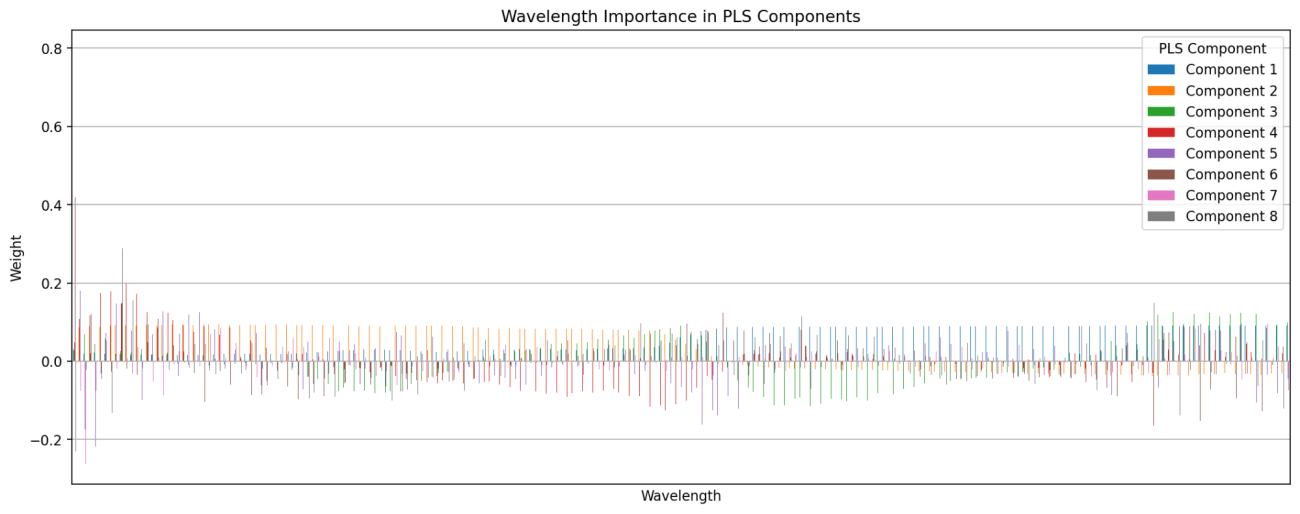
さらに、PLSは数理モデルなので線形回帰によって使用された重み付けを可視化することで特徴量の重要度や説明性を教えてくれます。波長分解能が高まったことで増えたバンドが本当に有効だったのかを検証することもできます。また、仮説がない状態でも優位性のある波長を見つけ出すヒントになるかもしれません。
EMITの解析例
最後に 、同じく NASAのEMITのハイパースペクトルデータも解析してみましょう。
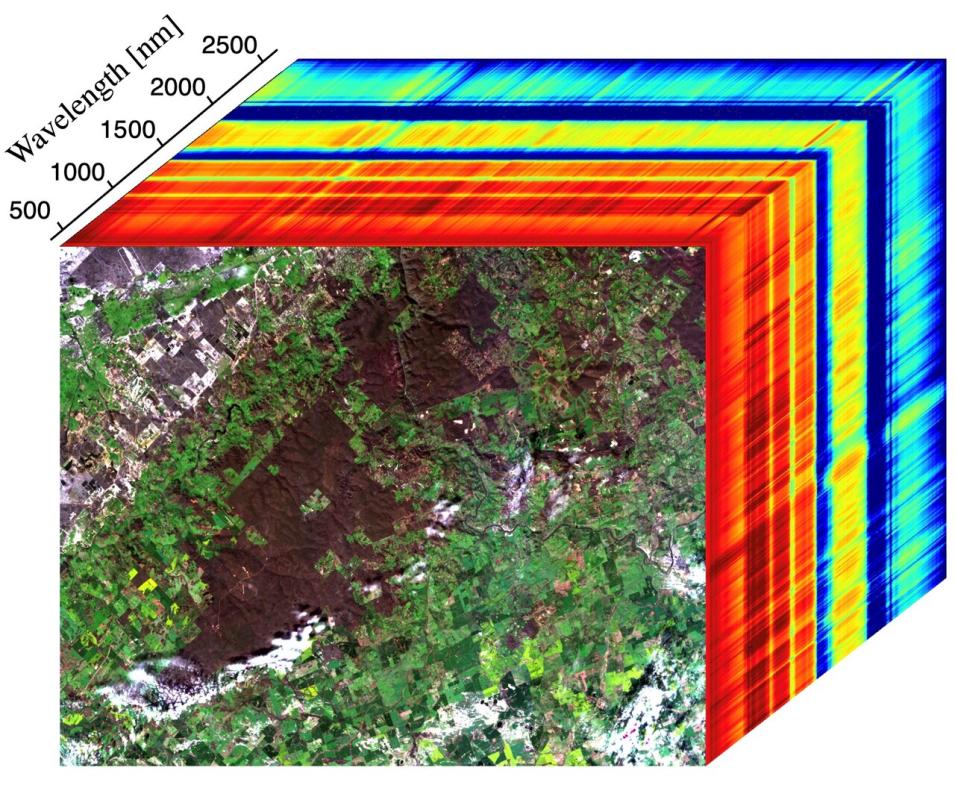
EMIT も NASA の Earth Data で取得が可能です。EMITも同様にダウンロードしてハイパースペクトルキューブの次元を確認します。
url = "https://github.com/opengeos/datasets/releases/download/netcdf/EMIT_L2A_RFL_001_20240404T161230_2409511_009.nc"
filepath = "data/EMIT_L2A_RFL_001_20240404T161230_2409511_009.nc"
hypercoast.download_file(url, filepath)
dataset = hypercoast.read_emit(filepath)
dataset
hypercube = dataset["reflectance"]
wavelents = dataset["wavelength"]
print(hypercube.shape)
(1894, 2227, 285)
こちらも解析する3地点とカラー画像を重ねて確認してみます。
P1 = (750, 750)
P2 = (700, 1400)
P3 = (600, 1200)
img = hypercube[:, :, [192, 64, 7]]
# nomalize by band
img = (img - img.min(axis=(0, 1 ))) / (img.max(axis=(0, 1))- img.min(axis=(0, 1 )))
img = np.clip(img, 0, 1)
img = (img * 255).astype(np.uint8)
# plot
plt.figure(figsize=(16, 10), dpi=120, facecolor="w", edgecolor="k")
plt.imshow(img, aspect="auto")
plt.scatter(*P1[::-1], color="r", s=100, label="P1", marker="x")
plt.scatter(*P2[::-1], color="c", s=100, label="P2", marker="x")
plt.scatter(*P3[::-1], color="y", s=100, label="P3", marker="x")
plt.title("Color Image")
plt.legend()
plt.tight_layout()
plt.savefig("data/output/emit_rgb.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()
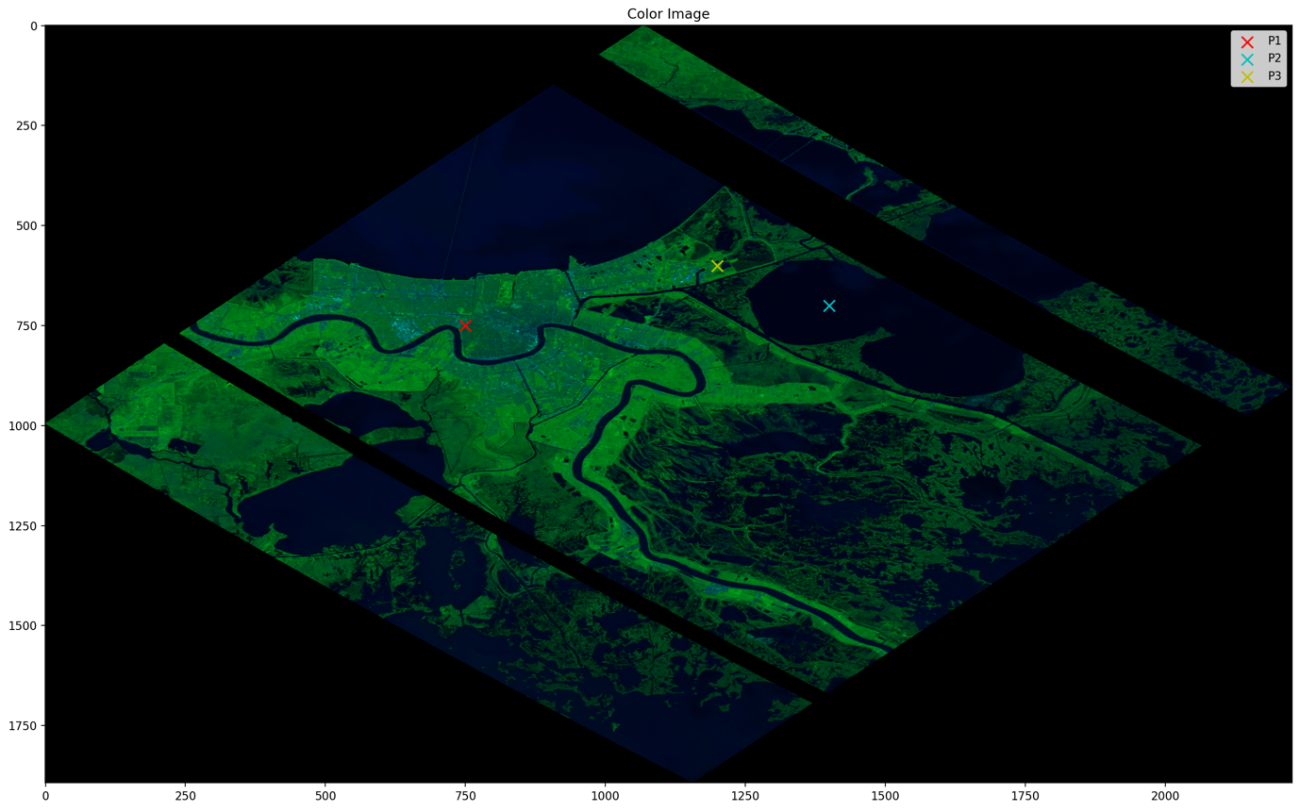
これらの3点の波長とそれぞれの反射強度を可視化します。
spectral_p1 = hypercube[P1[0], P1[1], :]
spectral_p2 = hypercube[P2[0], P2[1], :]
spectral_p3 = hypercube[P3[0], P3[1], :]
plt.figure(figsize=(16, 4), dpi=120, facecolor="w", edgecolor="k")
plt.plot(wavelents, spectral_p1, label="P1")
plt.plot(wavelents, spectral_p2, label="P2")
plt.plot(wavelents, spectral_p3, label="P3")
plt.title("Spectral Signature")
plt.xlabel("Wavelength")
plt.ylabel("Reflectance")
plt.legend()
plt.savefig("data/output/emit_spectral.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()
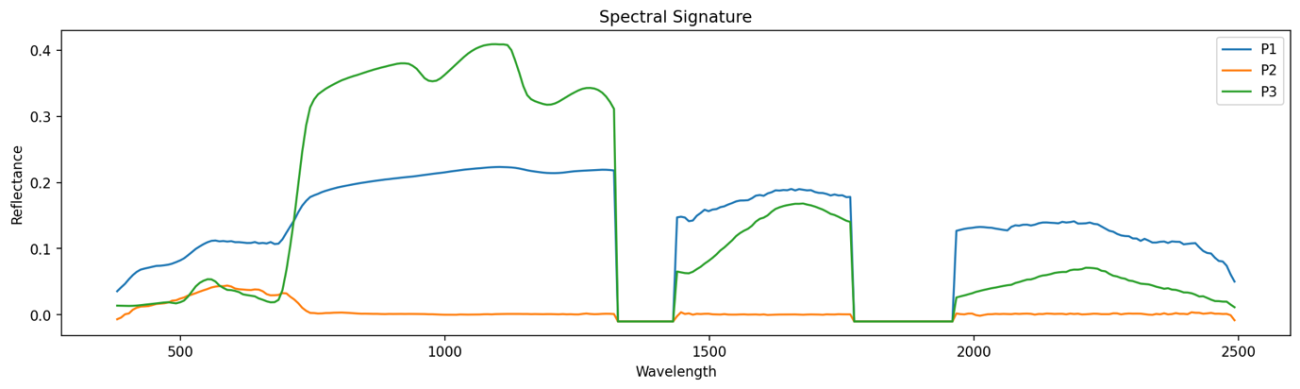
今回の解析では、このハイパーであるからこそのバンド数を利用した解析手法をご紹介します。Spectral Angle Mapper; SAMといってスペクトルの類似度を計算する手法です。
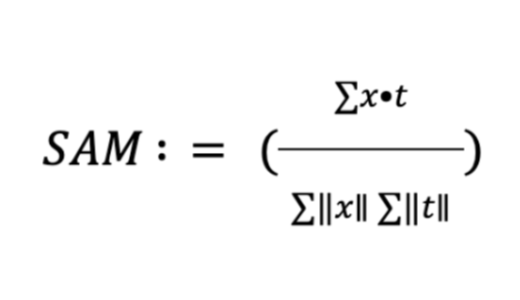
数式では複雑ですが、高次元ベクトル同士の間の角度を表しています。ベクトルが同じ方向を向いていると角度は小さくなります。スペクトルの形が似ていれば同じような性質を持つものと判定したりすることができます。SAMの良いところはベクトルの大きさで正規化するので反射強度にそこまで左右されにくいことです。
def spectral_angle_mapper(x, r):
cos_theta = np.dot(x, r) / (np.linalg.norm(x) * np.linalg.norm(r))
return np.arccos(np.clip(cos_theta, -1, 1))
Pythonでも定義をしたところで、P1と類似しているかどうかを計算していきます。まずはP1のサンプルを取得して平均的なスペクトルを求めます。このような参照する点のスペクトルを参照スペクトルといいます。
sample = 40
specrtal_reference = np.mean(hypercube[P1[0]:P1[0]+sample, P1[1]:P1[1]+sample, :], axis=(0, 1))
plt.figure(figsize=(16, 3), dpi=120, facecolor="w", edgecolor="k")
plt.plot(wavelents, specrtal_reference, label="Reference Spectral Signature")
plt.title("Reference Spectral Signature")
plt.xlabel("Wavelength")
plt.ylabel("Reflectance")
plt.legend()
plt.savefig("data/output/emit_reference.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()
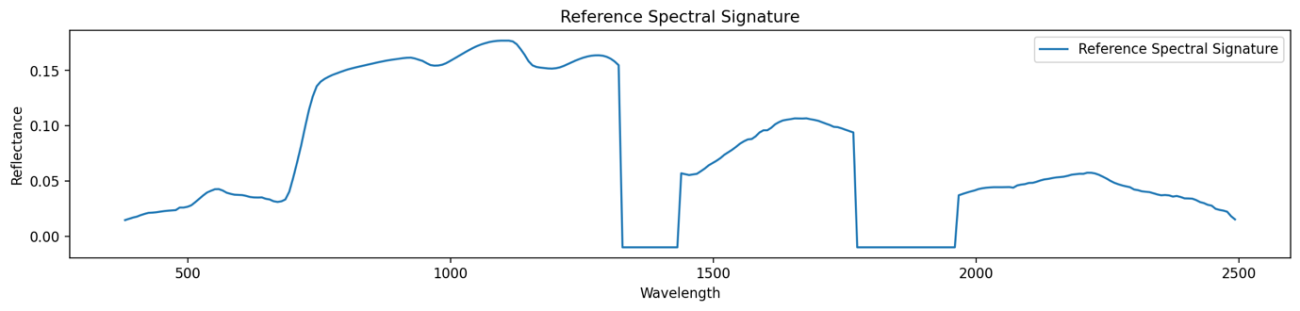
参照スペクトルとP1〜P3の周辺サンプルで類似性を判定していきたいと思います。加えて、参考のために、各点同士の平均誤差も算出します。当然、反射強度の差が大きければ異なる性質を持っているので単純に平均誤差も有効な判断基準になるからです。
P1_S = np.array(
hypercube[P1[0]:P1[0]+sample, P1[1]:P1[1]+sample, :]
).reshape(sample**2, hypercube.shape[-1])
P2_S = np.array(
hypercube[P2[0]:P2[0]+sample, P2[1]:P2[1]+sample, :]
).reshape(sample**2, hypercube.shape[-1])
P3_S = np.array(
hypercube[P3[0]:P3[0]+sample, P3[1]:P3[1]+sample, :]
).reshape(sample**2, hypercube.shape[-1])
sam_p1 = np.array([spectral_angle_mapper(_pnt, specrtal_reference) for _pnt in P1_S])
sam_p2 = np.array([spectral_angle_mapper(_pnt, specrtal_reference) for _pnt in P2_S])
sam_p3 = np.array([spectral_angle_mapper(_pnt, specrtal_reference) for _pnt in P3_S])
dif_p1 = np.array([np.linalg.norm(_pnt - specrtal_reference) for _pnt in P1_S])
dif_p2 = np.array([np.linalg.norm(_pnt - specrtal_reference) for _pnt in P2_S])
dif_p3 = np.array([np.linalg.norm(_pnt - specrtal_reference) for _pnt in P3_S])
# radian conversion
sam_p2 = np.rad2deg(sam_p2)
sam_p3 = np.rad2deg(sam_p3)
sam_p1 = np.rad2deg(sam_p1)
print("SAM P1: ", sam_p1.mean(), " SAM P2: ", sam_p2.mean(), " SAM P3: ", sam_p3.mean())
plt.figure(figsize=(16, 4), dpi=120, facecolor="w", edgecolor="k")
plt.scatter(dif_p1, sam_p1, label="P1", color="r", marker="x", alpha=0.5)
plt.scatter(dif_p2, sam_p2, label="P2", color="c", marker="o", alpha=0.5)
plt.scatter(dif_p3, sam_p3, label="P3", color="y", marker="*", alpha=0.5)
plt.title("Spectral Angle Mapper")
plt.xlabel("Reflectance Difference [Value]")
plt.ylabel("Spectral Angle [Degree]")
plt.legend()
plt.savefig("data/output/emit_sam.png", dpi=160, bbox_inches="tight")
plt.show();plt.clf();plt.close()
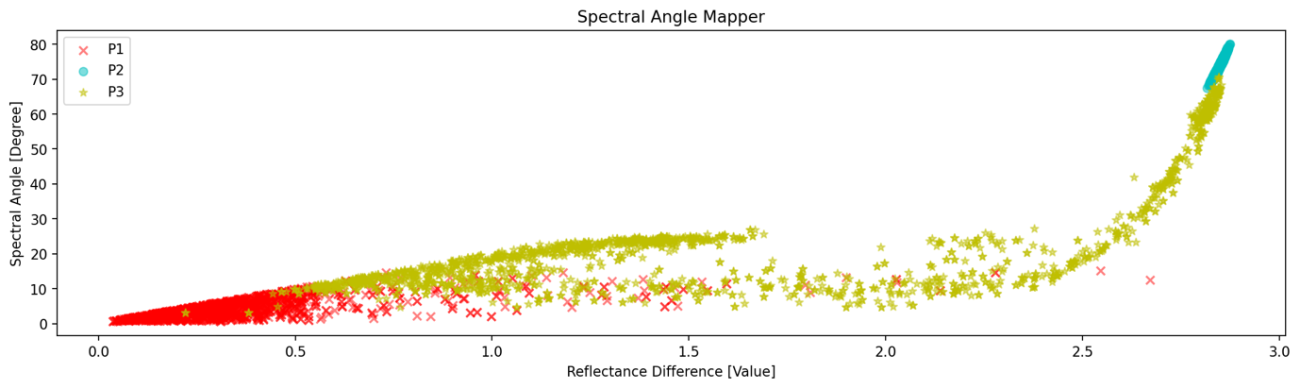
図では縦軸がSAMの角度、横軸が平均誤差の大きさを表しています。この図からはP1と参照スペクトルはほぼ同地点なので赤色と他の色の点が見分けたいことになります。P2の水色は明らかに分布が離れているので見極められそうです。P3も離れている分布も存在するので判断もできそうですが難しい点もあります。
実際のデータで異なる手法を使用することで特性もわかってきます。
P2(水色)と反射強度が全く異なる箇所を識別するためには、平均誤差を用いた手法が有効です。
しかしながら、P1(赤)とP3(黄)のように、平均誤差が同じように存在する領域でも、横軸の 2.5 あたりからP3の黄色のサンプルはSAMの値が大きく変化しており、P1とは異なることが分かります。
全体的なスペクトルの差だけではなく、近い波長でも同じような振る舞いをするハイパースペクトルだからこそできる考慮が計算に含まれているからです。
さらに興味を持った方はHISUIを提供している Tellusにふれてみてはいかがでしょうか。
https://www.tellusxdp.com/ja/catalog/data/hisui-promotion.html
まとめ
いかがだったでしょうか?
本記事を通して波長分解能による新たな視点が産まれましたら幸いです。理論的な背景を理解して、仮説を立てて解析して行くことで信頼される結果をもたらす解析者となることができるでしょう。宙畑は技術解説を今後も深ぼっていきたいと考えております。引き続きご愛読いただけますと幸いです。


