Pythonを使って人工衛星の軌道を表現する~軌道6要素、TLE~
人工衛星の軌道記事の第2弾!今回はPythonを使って人工衛星の軌道を表現していきます。
本記事では、前回の記事でご紹介した軌道の表現方法を実際に手を動かしながら学んでいきます。
事前準備
特に本記事ではTry JupyterのJupyterノートブックを用いて、実際に計算しながら解説を行います。まずはTry JupyterのURL(https://jupyter.org/try)にアクセスし、「Try JupyterLab」を選択し、[File]メニューから[New Notebook] – [Python3]をクリックして、Pythonのノートブック環境を開いてみましょう。ノートブックのセルに
print("Hello World!")と入力し、[Run]をクリック(あるいは,セルを選択した状態でShift+Enter)してみましょう。以下のような「Hello World!」という文字が表示されていれば、Try Jupyterの導入は成功です。
軌道の表現方法
目的地としての軌道を説明するに先立って、そもそも衛星や宇宙機はどのように軌道を描くのか説明します。
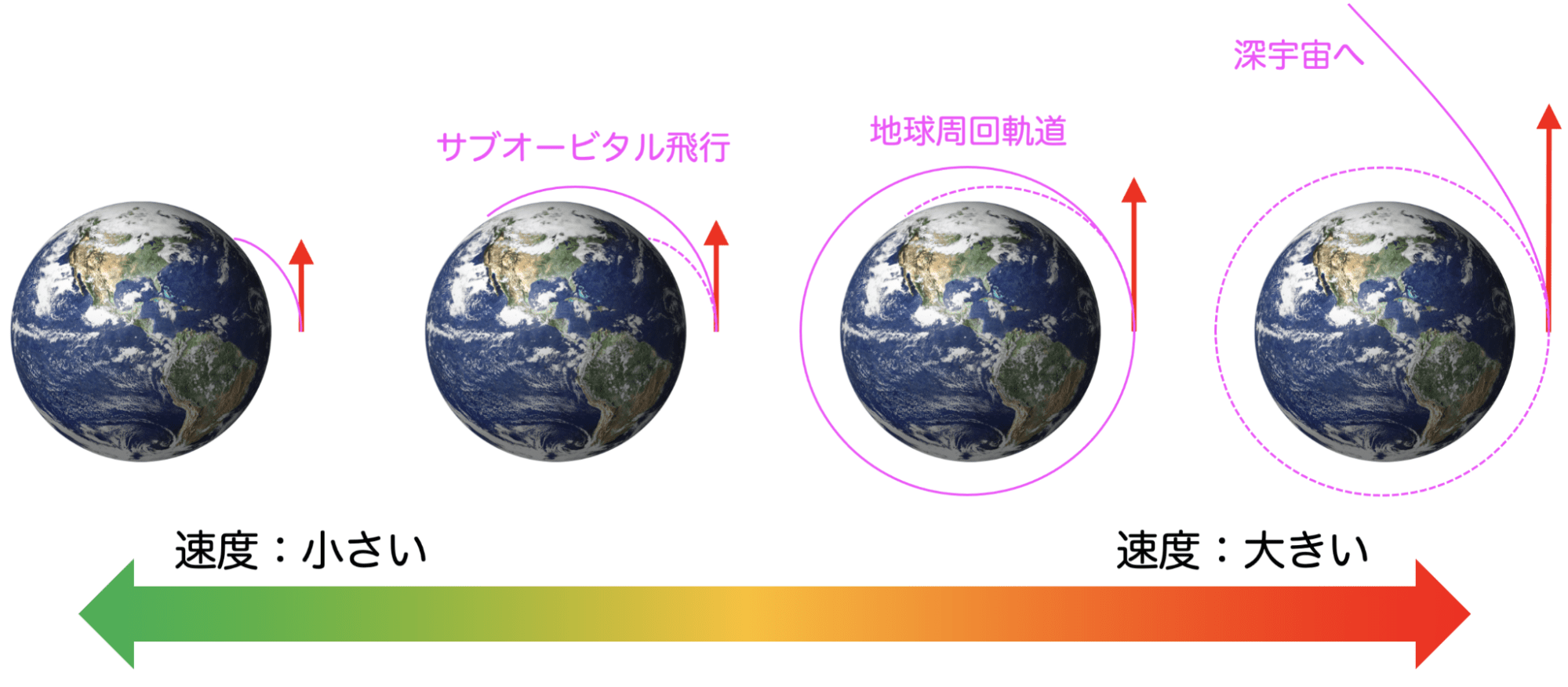
地上でボールを投げた場合、放物線を描いて地面に落ちます。このボールが描く軌道も衛星や宇宙機の軌道も全く同じ原理で運動しています(実際には,地上では大気抵抗の影響を受けるため、衛星や宇宙機より複雑な運動をしています)。
より速くボールを投げると、より遠くまで飛ばすことができるようになります。人類の身体能力には限界がありますが、人類は技術力を使えば、どんどん速く・どんどん遠くまで飛ばせるようになり、ついには高度100kmを超えて、宇宙空間まで飛ばせるようになります。
一度、宇宙空間に到達した後に、再び地上に落ちてきてしまう軌道が「サブオービタル」と呼ばれる種類の軌道です。
さらに速度を高めることができると、ついには宇宙空間に留まり続けることができるようになります。これが地球周回軌道と呼ばれる軌道であり、いわゆる地球周回の人工衛星が飛んでいるのはこの軌道です。
さらに速度を上げると、人工衛星は地球の重力から解き放たれて、深宇宙領域へ飛び出すことができるようになるのです。
ニュートンの運動方程式と軌道力学
少し理論的な話をしてみましょう(微分積分、ベクトル等の知識が必要となるため、この節は、興味の無い方は読み飛ばしても構いません)。地上で投げたボールや宇宙空間を飛ぶ人工衛星は、以下に示すニュートンの運動方程式に従って飛行します。
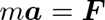
↓
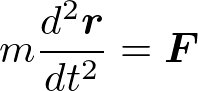
(mは探査機の質量、aは加速度ベクトル、Fは探査機に働く力、rは衛星の位置ベクトル、太字はベクトル量を表す)
特に地球周回の人工衛星の場合は、地球の重力を受けて運動しています。ニュートンの万有引力の法則を用いると、以下のように表現されます。
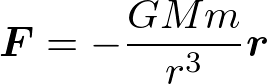
(Gは万有引力定数、Mは地球周回軌道であれば地球の質量、mは探査機の質量、rは地球中心から探査機までの距離、rの太字は地球中心から衛星の位置ベクトルを表す)
このニュートンの運動方程式を数値的に解くことで、人工衛星の軌道を計算することができます。短いプログラムで計算できるので、興味のある方はJupyterで以下のコードを走らせてみてください。さらにx0とtの値を変えると軌道がどのように変わるのかも試してみてください。
このように、ある時刻にある位置・速度で運動をしている人工衛星が、その後の時刻においてどの位置・速度にいるのかを計算することは、「軌道伝播(Orbit Propagation)」と呼ばれ、私たち専門家は日々、軌道伝播しています。地球など等の1つの天体の重力の影響を受けて運動する人工衛星の軌道の場合は、解析的に(簡単な数式で)軌道計算ができますが、より複雑な軌道伝播には数値計算が必要となります。
# Import Python Modules
import numpy as np # 数値計算ライブラリ
from scipy.integrate import odeint # 常微分方程式を解くライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ
# 二体問題の運動方程式
def func(x, t):
GM = 398600.4354360959 # 地球の重力定数, km3/s2
r = np.linalg.norm(x[0:3])
dxdt = [x[3],
x[4],
x[5],
-GM*x[0]/(r**3),
-GM*x[1]/(r**3),
-GM*x[2]/(r**3)]
return dxdt
# 微分方程式の初期条件
x0 = [10000, 0, 0, 0, 7, 0] # 位置(x,y,z)+速度(vx,vy,vz)
t = np.linspace(0, 86400, 1000) # 1日分 軌道伝播
# 微分方程式の数値計算
sol = odeint(func, x0, t)
# 描画
plt.plot(sol[:, 0],sol[:, 1], 'b')
plt.grid() # 格子をつける
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.show()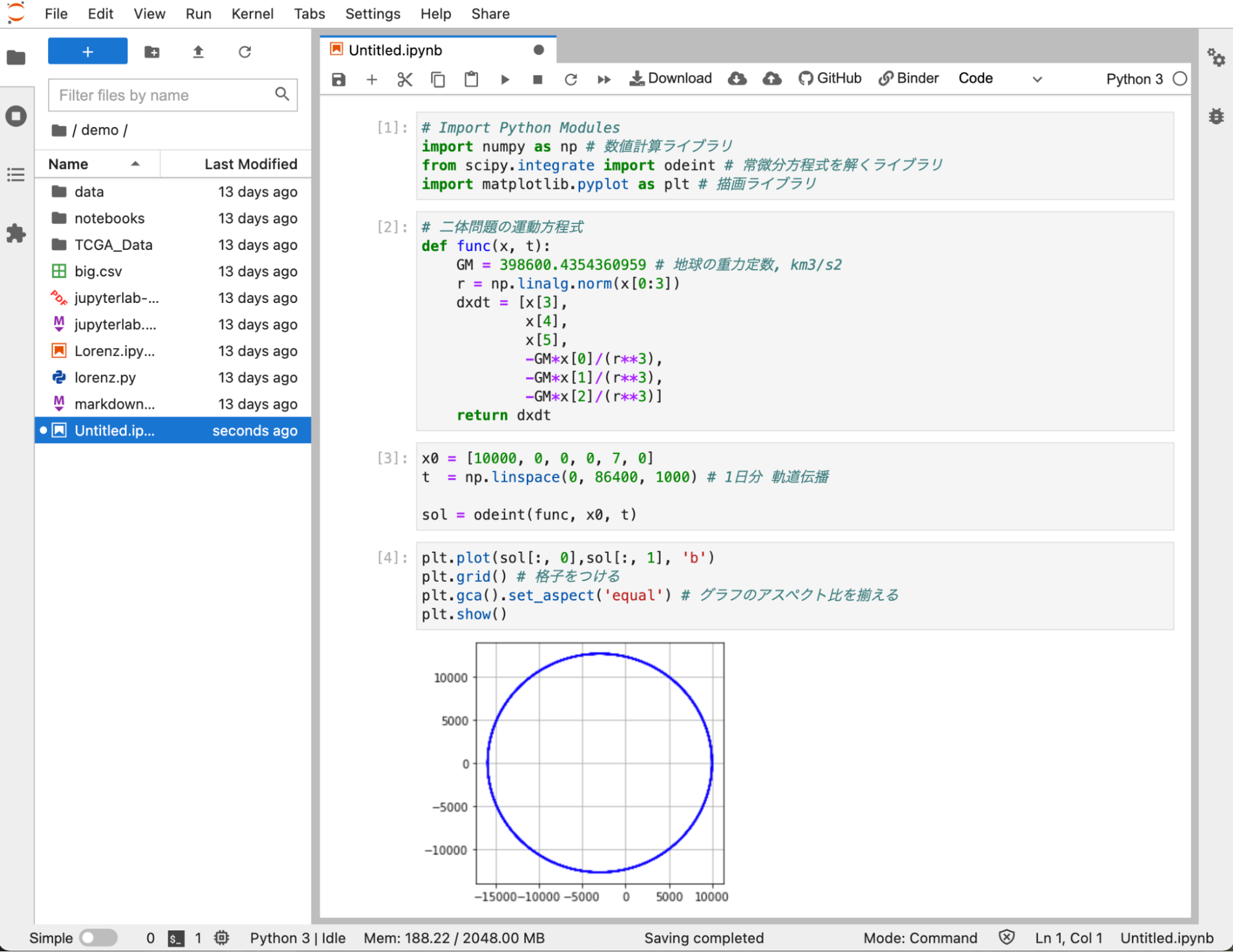
軌道6要素
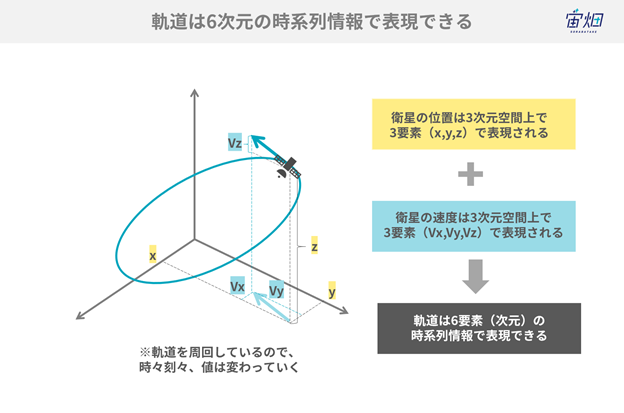
惑星や人工衛星の軌道は、3次元の位置と3次元の速度の合計6次元の時系列情報で表現することができます。
特に太陽の重力の影響のみ受けて運動する惑星は「楕円軌道」を描きながら運動することが、天文学者のヨハネス・ケプラーによって発見されました。
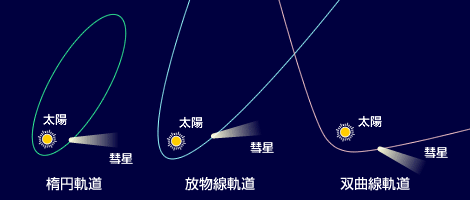
太陽などの1つの天体の重力の影響を受けて運動する物体の挙動を調べることを「二体問題」を解くと言い、二体問題で運動する物体は「楕円軌道」「放物線軌道」「双曲線軌道」のいずれかを描くことが知られています。
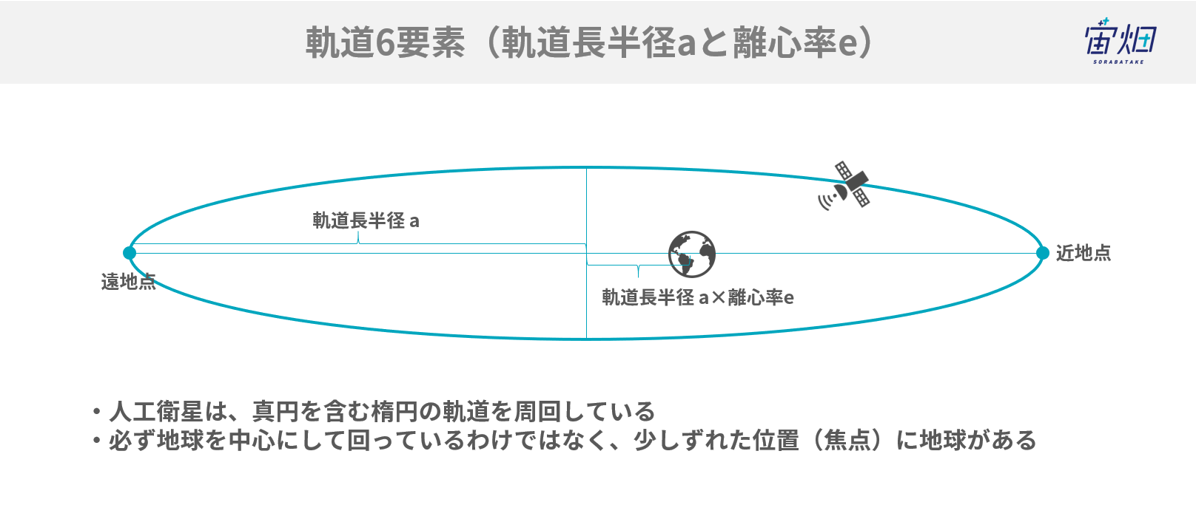
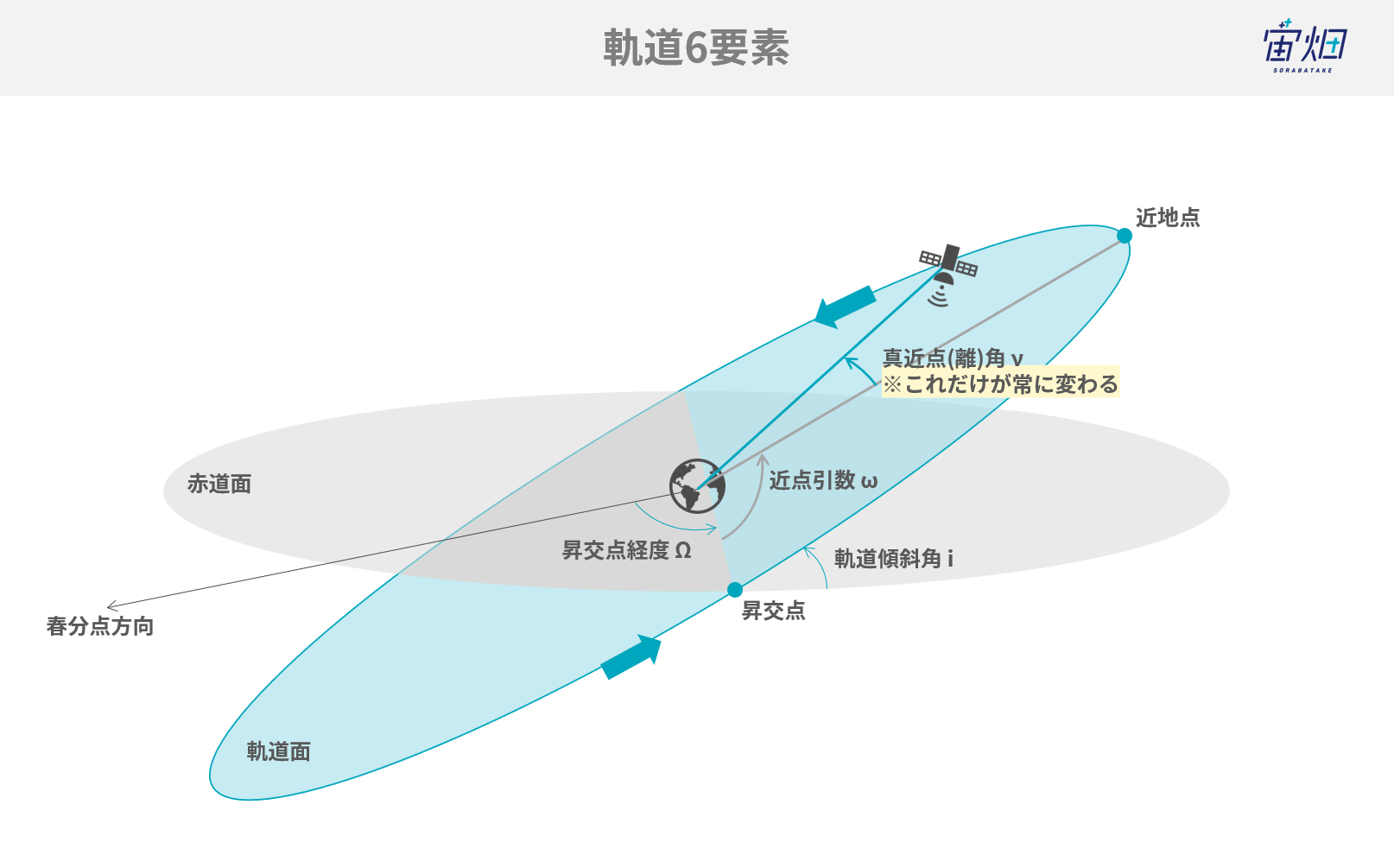
軌道が二体問題で運動するという性質を用いることで、惑星や人工衛星の軌道は、より扱いやすい情報で表現することができます。それが軌道6要素です。軌道6要素の取り方はバラエティがありますが、最もよく用いられる取り方が以下の6要素になります。
1.軌道長半径 a
2.軌道離心率 e
3.軌道傾斜角 i
4.昇交点経度 Ω
5.近点引数 ω
6.真近点(離)角 ν or 離心近点(離)角 E or 平均近点(離)角 M
それぞれの要素の詳しい説明は、ここでは割愛します。
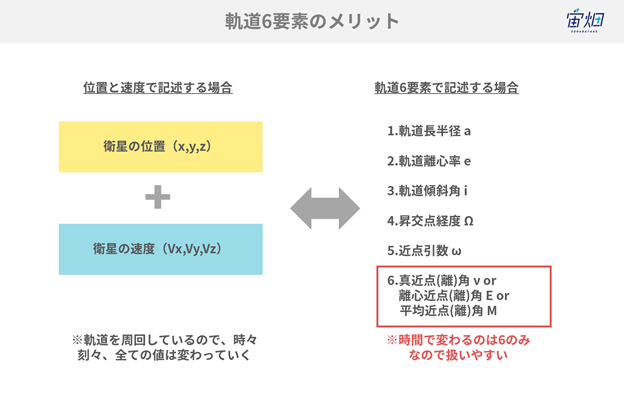
既に気づいた読者もいるかもしれませんが、軌道6要素がなぜ”6つ”あるのかというと、位置・速度の6次元情報を別の形式で表現しているからです。すなわち、位置・速度の6次元情報と軌道6要素は書き換えることが可能です。
では、なぜ敢えて軌道6要素で表現するかというと、二体問題で運動する物体は、軌道6要素の内の5つの要素(a, e, i, Ω, ω)が時間によって変わらないためです。
もちろん現実世界の人工衛星は、地球の重力の影響以外にも、太陽や月の重力、地球の大気抵抗、地球が真球ではないことで生じる力を受けているので、(a, e, i, Ω, ω)は時々刻々と変化します。それでも、変化量が少ない軌道6要素を用いる方が理論的には扱いやすい場面が多いです。
さて、Jupyterノートブックを用いて、実際に軌道6要素と位置・速度の書き換えをしてみましょう。本計算には、欧州宇宙機関ESAのAdvanced Concepts Team (ACT)が公開しているpykep(https://www.esa.int/gsp/ACT/open_source/pykep/)というライブラリを用います。まず以下のコマンドで、Jupyterノートブックにpykepをインストールしてみましょう(インストールには数十秒の時間を要します)。
!pip install pykep以下のような画面が表示されていれば,インストール成功です.
地球の軌道6要素は以下のような値 (参考:https://ssd.jpl.nasa.gov/txt/aprx_pos_planets.pdf)です。pykepでの計算の都合上、km、 radの単位形に書き直しています。
|
地球の軌道6要素
(太陽中心、黄道面基準座標系)
|
||
|
(au, deg)
|
(km, rad)
|
|
| 軌道長半径a | 1.00000261 au | 149598261.1504 km |
| 軌道離心率 e | 0.01671123 | 0.01671123 |
| 軌道傾斜角 i | -0.00001531 deg | -2.6720990848033185e-07 rad |
| 昇交点経度 Ω | 0.0 deg | 0.0 rad |
| 近点引数 ω | 102.93768193 deg | 1.796601474049171 rad |
| 離心近点角 E | 計算したい時刻による | 計算したい時刻による |
pykepのpar2icという関数を用いて、軌道6要素を位置r・速度vに変換します。なお、変換には太陽の重力定数を用いる必要があるため、132712440041.9393 km3/s2という値を用います。インストールしたpykepのモジュールを利用するためには、モジュールをインポートする必要があるので注意です。
import pykep as pk
GM = 132712440041.9393 # km3/s2
r, v = pk.par2ic([
149598261.1504, # a, km
0.01671123, # e, -
-2.6720990848033185e-07, # i, rad
0.0, # O, rad
1.796601474049171, # w, rad
0.0 # E, rad
], GM)
print(r, v)(-32934004.25725372, 143364076.19608086, -38.308301679723) (-29.51776907469439, -6.780906055160861, 1.8119252864133049e-06)
という値が出力されたでしょうか?これが離心近点角E=0 (地球が太陽の最も近くを通過するとき)における地球の位置・速度になります。逆に位置・速度が与えられると、pykepのic2parというモジュールを用いて、軌道6要素を得ることができます。
では、離心近点角Eを軌道一周分だけ変化させて、描画ライブラリで結果を表示してみましょう。これで、地球の楕円軌道(と言っても、ほとんど円軌道ですが)が描くことができました。
import numpy as np
import matplotlib.pyplot as plt # 描画ライブラリ
import pykep as pk
GM = 132712440041.9393 # km3/s2
ea_all = np.linspace(0, 2*np.pi, 1000) # 0 to 2pi radian
pos = np.array([
pk.par2ic([
149598261.1504, # a, km
0.01671123, # e, -
-2.6720990848033185e-07, # i, rad
0.0, # O, rad
1.796601474049171, # w, rad
ea_t # E, rad
], GM)[0] # 位置のみを取り出す
for ea_t in ea_all
]) # Pythonのリスト内包表記を用いて,一括で計算
# 描画
plt.plot(pos[:,0],pos[:,1], 'b')
plt.grid() # 格子をつける
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.show()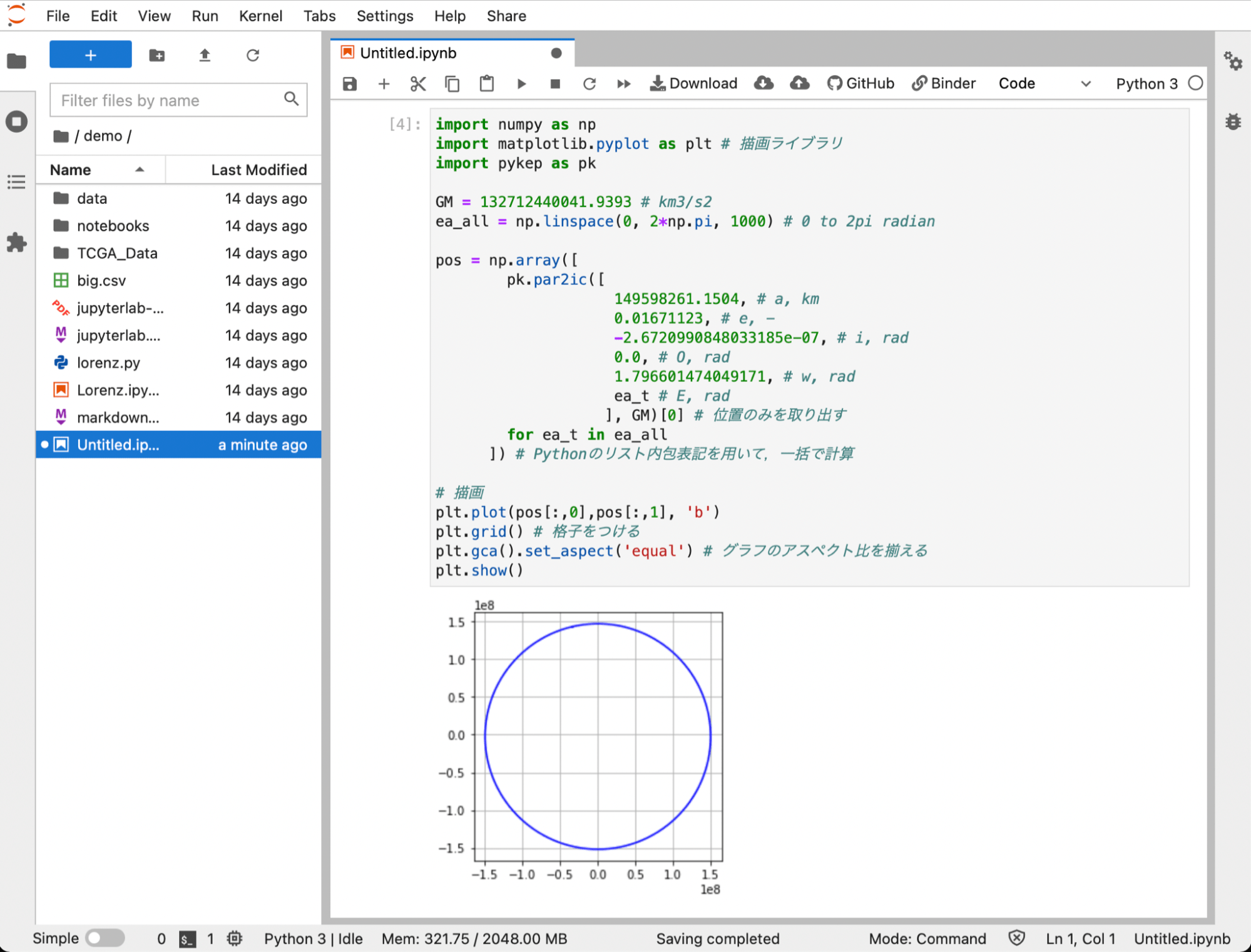
私たち専門家が地球等の惑星の位置・速度を計算するためには、軌道6要素から計算するのではなく、エフェメリス(天体歴)からNASA JPLが提供するSPICE等のライブラリ(https://naif.jpl.nasa.gov/naif/toolkit.html)を用いて、計算しています。このエフェメリスを用いると、複数の天体重力の影響等が考慮された高精度な位置・速度を計算することができます。spiceypy (https://github.com/AndrewAnnex/SpiceyPy)というPython用のライブラリも提供されているため、興味のある方は利用してみてください。
2行軌道要素形式(Two-Line Elements: TLE)
地球周回衛星の人工衛星(の中でも特に高度が低いものを中心に)の軌道を表すデータフォーマットとして、2行軌道要素形式(Two-Line Elements: TLE)というものが用いられることがあります。
TLEとは、NASAや北アメリカ航空宇宙防衛司令部(NORAD)が現在でも利用している地球中心の軌道6要素等をまとめたデータフォーマットです。

各衛星のTLEはNORADのCelestrakというウェブサイトで公開されています(http://www.celestrak.com/NORAD/elements/)。例えば、国際宇宙ステーション(ISS)のTLEはCelestrakのSpace Stations (http://www.celestrak.com/NORAD/elements/stations.txt)のページから取得することができます。2021/08/15現在のISSのTLEは以下の通りです。
ISS (ZARYA)
1 25544U 98067A 21226.49389238 .00001429 00000-0 34174-4 0 9998
2 25544 51.6437 54.3833 0001250 307.1355 142.9078 15.48901431297630
TLEで表された軌道情報は、SGP4 (Simplified General Perturbations Satellite Orbit Model 4)等の計算アルゴリズムを用いて、位置・速度に換算することが多いです。SGP4の計算アルゴリズムは、Pythonライブラリとしても与えられているので、Jupyterノートブックを用いて、計算してみましょう。
SGP4のライブラリをインストールするには、以下のコマンドを実行します。
!pip install sgp4ISSの位置、速度を計算してみよう。
from sgp4.api import Satrec, jday
# ISSのTLE
s = '1 25544U 98067A 21226.49389238 .00001429 00000-0 34174-4 0 9998'
t = '2 25544 51.6437 54.3833 0001250 307.1355 142.9078 15.48901431297630'
# SGP4による位置・速度の計算
satellite = Satrec.twoline2rv(s, t)
jd, fr = jday(2021, 8, 15, 0, 0, 0)
e, r, v = satellite.sgp4(jd, fr)
# 結果の出力
print(r) # True Equator Mean Equinox position (km)
print(v) # True Equator Mean Equinox velocity (km/s)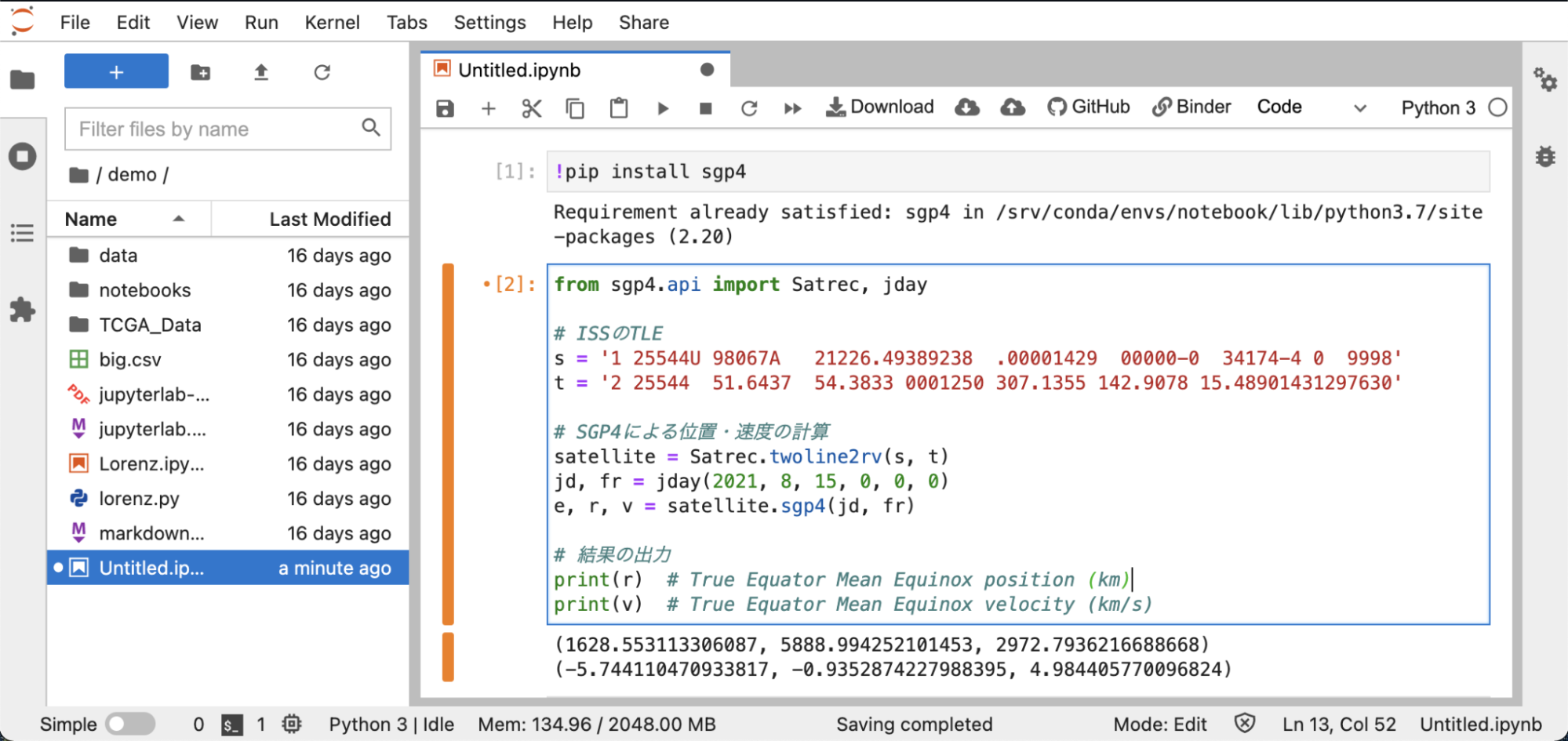
ここまで、人工衛星の軌道がpythonを使ってどのように表現されるのかをご紹介しました。
次回の記事では、今回学んだ表現方法を使って実際によく使われる軌道の種類について、ご紹介していきます。


